Bhushan B. Handbook of Micro/Nano Tribology, Second Edition

Подождите немного. Документ загружается.

discussion, see Pethica and Sutton, 1995). The decay of this interaction is described by a function i(z),

where z is the distance between the surfaces. The surfaces of tip and sample are parameterized by T(x)

and S(x), respectively. To simplify the model further, we will restrict the analysis to one dimension. The

total interaction between tip and sample is then

(6.15)

The term ∆ takes account of the scanning, that is, by varying the distance ∆, the relative position of tip

and sample is changed. Assuming some geometry for the tip and for the sample, this integral can be

solved. A general geometry for an SPM setup on an atomic scale is a slowly varying corrugated surface

where a

is the corrugation of the surface, k

the corresponding reciprocal lattice vector, and h a function

which describes the slow variation of the surface height (that is, h' (x)  k

). The tip is assumed parabolic

with an atomic corrugation,

where a

is the corrugation of the tip, R the tip radius, and a

cos (k

x) a term which is introduced

phenomenologically. Such a term could arise from interaction with the surface and would describe, for

example, a ﬂake of surface material picked up by the tip or some sort of reconstruction on the tip induced

by the surface. This term has the same periodicity as the surface and it seems reasonable that only one

of the terms a

or a

is important for a given tip–sample system. In the case of contact mode SFM and

SFFM the tip and the surface are deformed and a mechanical contact of radius r

is formed (see

Section 6.4.2). Then, the main interaction is through the contact area; therefore, the term describing the

parabolic tip can be omitted and the integral can be evaluated only cover the contact radius. A Taylor

expansion of the interaction around a mean height h

(x – ∆) up to second order leads to

where h

(x – ∆) is a mean height and δh (x – ∆) = a

cos (k

(x – ∆)) – a

cos (k

(x)) – a

cos (k

(x)).

This integral can be interpreted in terms of the mean value of the integrand averaged over the contact

radius r

If the contact radius is large compared to the periodicity of the lattice, then the term 〈δh (∆)〉

vanishes

and the only nonvanishing term in 〈δh

(∆)〉

is due to 〈a

cos (k

(x – ∆)) · a

cos (k

(x))〉

. Therefore,

the total interaction is

IiTxSxdx

tot

∆∆

()

−−

()

−∞

+∞

∫

Sx a k x hx

−

()

=−

()

+−

()

∆∆∆cos ,

Tx a kx x R a kx

T T TS S

()

cos cos ,

Iihx

hx dx

tot

∆∆∆∆

()

−

()

∂

−

()

∂

−

()













−

∫



δδ,

Irih

tot

∆∆∆ ∆

()

∂

()

∂

()













 2

δδ.

Irih

aa k

STS S

tot

∆∆ ∆

()

∂

()













 2

cos ,

from which we see that, under the assumptions made, the atomic periodicity is “resolved” as the tip scans

the sample — that is, as ∆ is varied — even though the “true” resolution is much less, namely, of the

order of the contact radius. To resolve the atomic periodicity with a large contact radius, the term a

which was introduced above has to be nonzero; the tip therefore has to have the same periodicity as the

surface. To achieve “true” atomic resolution within this simple model, the contact radius would have to

be reduced to atomic dimensions and the tip would have to be sharp enough, which is what is expected

intuitively. If this is the case, however, the term 〈δh (∆)〉

does not necessarily vanish and thus the integral

15 should be computed without approximations.

6.4.2 Deformation of Tip and Sample

The deformation of tip and sample is fundamental to the adhesion and friction of any contact, including

the special case of an SFM or SFFM setup. To describe these deformations, continuum theories are

generally used. A detailed description of contact mechanics can be found in Johnson (1985). The ﬁrst

approach to contact mechanics is due to Hertz (1881). He showed that two elastic solids of radii R

and

pressed against each other with a loading force F

deform elastically and touch on a circle of radius

(6.16)

where R

is an effective radius such that 1/R* = 1/R

+ 1/R

and E

is an effective modulus of elasticity

such that 1/E* = (1–ν

)/E

+ (1–ν

)/E

, with E the modulus of elasticity and ν Poisson’s ratio. In the case

of SFM and SFFM, the sample is assumed ﬂat and the tip of radius R

tip

, and correspondingly R

= R

tip

Due to the elastic deformation, distant parts of the two bodies approach each other by a distance δ =

. With Equations 6.16 this relation can be restated as

from which the amount of elastic energy V

(δ) stored in the system is computed by integration:

and the stiffness c

con

of the contact by differentiation:

(6.17)

The elastic energy V

(δ) can be interpreted as a repulsive surface potential which acts only after tip and

sample have touched. It should be noted, however, that the distance δ is not directly the indentation

distance of the tip. Another important magnitude is the pressure distribution p(r) in the contact region:

If in addition to the normal loading force a lateral force F

lat

is applied to the tip and if the friction is high

enough to prevent slip, then the tip–sample contact will be deformed laterally. The corresponding lateral

displacement of the contact is (Johnson, 1985):













FRE

δδ

()

=⋅⋅

VRE

δδ

()

=⋅⋅

cREEr

ccon

δδ

()

=⋅⋅=⋅22

()

π⋅

−













where G

is an effective modulus of elasticity such that 1/G

= (2 – ν

)/G

+ (2 – ν

)/G

, G

and G

are

the shear moduli of tip and sample, respectively, and ν

and ν

the corresponding Poisson ratios. The

lateral stiffness of the contact is then

(6.18)

And, ﬁnally, the shear stress in the contact region is

The Hertz theory does not account for surface forces and adhesion. Due to these surface forces, bodies

adhere to each other and will be deformed slightly by adhesion forces. The adhesion force of a sphere

or a parabolic tip on a ﬂat surface is (Israelachvili, 1992)

(6.19)

where R is the tip radius and γ is the surface energy. This attractive adhesion force acts in addition to

any external load. Therefore, the simplest way to take into account adhesion in the deformation of the

tip–sample contact is to deﬁne an effective normal force as F

= F

load

+ F

, and to apply Equation 6.16

with this effective normal force. At zero load the contact radius is then (3πγR

)

1/3

. This approach is

appropriate if the deformation of the tip–sample contact induced by surface forces is small compared

with the deformation due to the contact forces, which is the case if the two bodies are sufﬁciently rigid.

If, on the contrary, the surface forces are not negligible, then the exact shape of the contact will differ

from the one predicted by the Hertz theory. One way to account for the surface forces is to allow the

tip–sample contact to deform in order to increase the contact area and thus the surface energy. The shape

of the tip–sample contact is then determined by the balance between the elastic energy needed to deform

the contact and the surface energy gained as the contact forms. This is the basic idea behind the JKR

theory (Johnson, 1971), which predicts a contact radius

(6.20)

with F

= 3πγR. For vanishing surface energy, the Hertz relation is recovered. For a nonvanishing surface

energy, the JKR theory predicts an adhesion force –F

, which is lower than the adhesion force predicted

by the Hertz theory. According to Equation 6.20, the minimum contact radius r

min

= (3R·F

/4E

)

1/3

obtained with a tensile force F = –F

. Due to surface forces, a neck forms between tip and sample which

becomes unstable if the minimum contact radius is reached. This is especially relevant in SFM and SFFM

because it means that, unlike in the case of the Hertz theory, the contact radius cannot be reduced to

atomic dimensions by compensating the adhesion force adequately.

The JKR theory describes adhesion by means of the surface energy. For a complete description of the

contact problem, the ﬁnite range of the surface forces has to be taken into account. Forces act not only

in the contact region, but also further out, where the two bodies are not in direct mechanical contact

lat

⋅

crG

clat

=⋅8

()

π⋅

−

























−

lat

=π⋅⋅4 γ ,

⋅

++ +

























221

ad ad

but separated by distances so small that interaction forces are still present. The exact shape of the whole

contact is then determined by the balance of forces due to the surface potential and due to the elastic

deformation of tip and sample. Furthermore, most approaches neglect lateral forces, which are only

treated in very recent studies (Johnson, 1997a,b). A more-detailed description of these theories can be

found in Chapter 5 by Burnham.

6.4.3 Modeling of SFM and SFFM: Energy Dissipation

on an Atomic Scale

For a detailed understanding of an instrument, a model is usually developed that retains its fundamental

properties but is still as simple as possible. In the present section, such a model will be discussed for

SFM and SFFM (Zhong and Tománek, 1990; Tománek et al., 1991; McClelland and Gosli, 1992; Colchero

and Marti, 1995; Colchero et al., 1996b; as well as Gyalog et al., 1995). To keep ideas simple, the model

will be restricted ﬁrst to one dimension; therefore the behavior normal to the surface and the behavior

lateral to the surface will be analyzed separately. From an experimental point of view, in an SFM only

the behavior normal to the surface is important. On the other hand, from the theoretical point of view,

any SFM is also an SFFM: for nonvanishing friction, lateral forces always act on the tip independently

of whether these forces are measured or not.

6.4.3.1 Modeling Energy Dissipation

Energy dissipation in SFM and SFFM can be understood in terms of a simple spring model: two springs

held together, for example, by magnets at one end and attached to rigid supports at the other. As the

supports are separated, potential energy is stored in the springs. Since the force on each spring is the

same, one ﬁnds F = ∆

= ∆

. The energy stored E

in each spring can therefore be written as

(6.21)

and the total energy is E

tot

= E

+ E

= (1/c

+ 1/c

/2, from which the effective spring constant of the

total system is determined as

(6.22)

The energy stored in each spring (see Equation 6.21) scales as

(6.23)

Correspondingly, most energy is stored in the weakest spring. If the springs are separated enough and

the springs break apart, the elastic energy stored in each spring will be converted into kinetic energy.

Since the total system is now separated into two springs that cannot interact with each other any longer,

the energy is ﬁnally dissipated within each spring. The energy is therefore dissipated according to

Equation 6.23.

This simple model can be applied directly to an SFM setup; each component that can store elastic

energy is represented by a spring with the corresponding force constant (see also Equation 6.30). Usually,

in SFM the cantilever is the softest spring, so that the most energy is dissipated in the cantilever. However,

the other extreme — the cantilever being the stiffest spring — is also possible as, for example, in STM.

In STM the tip is ideally stiff, but snapping still occurs due to the intrinsic elasticity of the tip–sample

contact (Smith et al., 1989). In this case all the energy dissipated during snapping into and out of contact

is dissipated in the microscopic degrees of freedom of the tip–sample system.

=⋅= =∆ ,and, correspondingly,

111

ccc

tot

=+.

= .

6.4.3.2 SFM and Normal Forces

A simple model for an SFM is shown in Figure 6.30. The main components are the tip, a spring, its rigid

support, and the sample to be studied. It is fundamental to note that the rigid support and not the tip

is moved with respect to the sample surface. Three different distances are relevant in this model: the

tip–sample distance z, the deﬂection d of the spring, and the separation ∆ between the rigid support and

the sample. However, only two of these distances are independent, since d = z –∆. The separation ∆ is

the distance that is controlled experimentally, z the distance usually used to describe the tip–sample

interaction as a function of distance, and d the deﬂection measured. In the present discussion, z and ∆

will be chosen as independent parameters which determine the state of the SFM setup. To determine the

behavior of the system, a standard analysis in terms of classical mechanics for zero temperature will be

presented (for T ≠ 0, see Dürig et al., 1992). The total energy of the tip–sample contact is determined

by the elastic energy V

(d) stored in the system as well as by the potential energy V

surf

(z) of the tip in

the surface potential. The elastic energy will ﬁrst be assumed to be due to the elastic energy of the spring

representing the cantilever, V

(d) = c · d

/2. In this case, the total energy is

(6.24)

In the right part of the equation, the total energy has been written in terms of the two independent

parameters z and ∆. In a typical SFM setup, the separation ∆ is controlled experimentally, but the tip is

free to move to an equilibrium position by varying its tip–sample distance, z; therefore, the force

equilibrium condition is

(6.25)

This force equilibrium condition determines the tip–sample distance z

for each separation ∆. If this

separation is varied, in general the equilibrium distance also varies. By solving Equation 6.25 for different

separations ∆, the curve z

(∆) is evaluated, which is fundamental to the behavior of the tip–sample

contact. To have stable equilibrium, Equation 6.25 is not sufﬁcient; in addition,

(6.26)

has to hold. For repulsive potentials, that is, if the force increases as the distance is decreased, this condition

is always fulﬁlled. However, for sufﬁciently attractive potentials, this relation will fail. Then, the tip jumps

onto the surface.

The tip–sample behavior can be illustrated as follows. Consider the two-dimensional energy surface

tot

(z, ∆) shown in Figure 6.31. Any possible conﬁguration of the tip–sample contact is represented by

FIGURE 6.30 Simple model for a typical SFM setup. The surface poten-

tial V

surf

(z) and the potential V

(d), which represents the elastic energy

stored in the system, are represented by springs. (From Colchero, J. et al.

(1996), Tribol. Lett. 2, 327–343. With permission.)

VzdVzcdVzcz Vz

tot surf surf tot

,,.

()

+⋅=

()

+⋅−

()

∆∆

dV z

tot

tot surf

.∆

∆

()

=−

()

=−

()

−⋅ −

()

= 0

dV z

tot eq

tot eq surf eq

∆

∆∆ ∆

()

a point on this energy surface corresponding to the coordinate (z, ∆) and to an energy V

tot

(z, ∆). For

each ﬁxed separation ∆

, the curve V

tot

(z, ∆

) is an energy curve on which the tip can move to minimize

its energy. The equilibrium condition, together with the stability condition (Equation 6.26) and the

additional assumption that the tip movement is “quasi-static” (the tip does not oscillate), restricts the

possible conﬁgurations to the local minima of these curves, that is, to the valleys seen in Figure 6.31. As

the separation ∆ is varied, the tip–sample contact will evolve to a new equilibrium position in the same

valley. If the system, however, is moved past the end of a valley, it will not be stable and move to the

other valley. Since this other valley is lower than the end point of the ﬁrst valley, the system will oscillate

around the new minimum until its kinetic energy is damped. We will assume that some damping

mechanism exists and will discuss its nature below. If the separation ∆ is varied in a sufﬁciently large

cycle, the system will evolve along the curve V

tot

(∆),∆) indicated by the solid line in Figure 6.31. The

projection of this curve onto the (z, ∆)-plane deﬁnes the curve z

(∆), which is the tip–sample separation

as a function of the separation ∆.

For a given surface potential the tip–sample distance z

(∆) can be constructed uniquely from the

equilibrium condition and from the stability condition. In a typical SFM experiment, the force — more

precisely, the deﬂection of the cantilever — is measured as the separation ∆ is varied. This so-called force

vs. distance curve (Weisenhorn et al., 1989) does not correspond to the force curve F(z), but to

Another important question is the energy that is dissipated during the acquisition of one force vs.

distance curve. This energy is the area enclosed by the force vs. distance curve and can be written as

In the discussion above, the deformation of the tip–sample contact was not taken into account. The

elastic energy was described only by the harmonic potential of the spring. The model can be generalized

FIGURE 6.31 Energy surface that describes the state of an SFM tip–sample system. The coordinate ∆ describes the

experimentally controlled distance between the sample and the base of the cantilever. The coordinate z represents

the tip–sample distance. As the distance ∆ is varied, the system evolves along the solid curve in one of the two valleys.

The system becomes unstable at the high end of a valley and moves to the lower valley. The projected curve z(∆) in

the (∆, z)-plane visualizes the hysteresis of the system. (From Colchero, J. et al. (1996), Tribol. Lett. 2, 327–343. With

permission.)

Fcz

dV z

∆∆∆

∆

()

=⋅

()

−

()

=−

()

surf eq

EFd=

()

∫

∆∆.

to account for the elastic energy stored in the tip–sample contact by introducing the corresponding

potential (Colchero et al., 1996b). Within this generalized model, the total elastic energy stored in the

SFM setup can be approximated by assuming that this energy is stored in an effective spring with an

effective force constant c

eff

deﬁned by

where c

con

= 2E

·r

is the stiffness of the tip–sample contact (see Equation 6.17).

To illustrate the formal description of the SFM setup presented above and to analyze the dissipation

of energy, a typical force vs. distance curve will be discussed in physical terms (see also Tabor, 1992).

First, the tip is far from the sample, feels no surface potential, and is not deﬂected. As the (base of the)

cantilever approaches the sample, surface forces begin to act. Due to the attractive surface potential, the

tip approaches the surface more than the increase of the separation: δz = δ∆ + δd, where δz is the increase

in tip–sample distance, δd the increase in deﬂection, and δ∆ the increase in separation. Eventually, the

spring is not “strong” enough to hold the tip and the tip jumps onto the surface. During this process,

the tip is ﬁrst accelerated, then hits the surface, and is suddenly stopped. This will induce vibrations of

the cantilever, but also a sudden elastic deformation of the microscopic tip–sample contact, which in

turn will result in elastic waves propagating out of the tip–sample contact. After some time, the kinetic

energy gained by the tip during the snapping process will be effectively removed from the tip–sample

system either into the macroscopic cantilever or into the two solids tip and sample. A similar process

happens when the tip is separated from the sample. Due to adhesion, the tip sticks to the sample. Elastic

energy is built up in the deformation of the cantilever, but also in the microscopic deformation of the

tip–sample contact. When this contact breaks, the cantilever will vibrate and the elastic deformation of

the tip–sample contact will relax. Again, the elastic energy stored in the system will be converted into

kinetic energy of the cantilever, or into waves in the tip and the sample, and will in the end be dissipated

due to some kind of friction (for example, internal friction in the solids or air damping in the case of

the cantilever).

6.4.3.3 SFFM and Lateral Forces

In the preceding section a general model for an SFM setup was described. However, this model was

applied only to study the behavior of the tip–sample system as the tip approaches the sample. In the

present section, the model will be applied to study the behavior of the tip–sample contact as the separation

between the support and the sample is varied in a direction parallel to the surface (Zhong and Tománek,

1990; Tománek et al., 1991). This is the situation that corresponds to the usual scanning motion of the

tip. Essentially, the description is as before: the tip is attached to a rigid support by means of a spring

and the sample is moved relative to this support by varying the separation ∆

. Again, the tip position is

not controlled directly, but follows from the equilibrium condition. The only difference compared to the

description above is that in order to describe the atomic corrugation of the surface, a surface potential

with the periodicity of the sample is assumed. Ideally, this is the potential that a perfect tip with only

one atom at its apex would “see,” and can be computed from ﬁrst principles. However, also if a nonideal

tip is in contact with the sample on an area with radius r

the effective interaction between tip and sample

will show a modulation with lattice spacing (see Section 6.4.1). The total potential seen by the tip is

therefore (Tománek et al., 1991).

(6.27)

where E

is the amplitude of the surface potential, k the reciprocal lattice vector of the surface, and c

the

force constant of the system. The stability condition for this potential is c

> E

· k

; therefore, if the

amplitude of the surface potential is sufﬁciently large, the range of postions with |x| < cos

–1

(c/E

· k

)/k

111

ccc

eff tip con

=+ ,

Vx E kx

xtot

, cos ,∆∆

()

+⋅−

()

will be unstable. From the equilibrium condition and the stability condition, the curve x(∆

) as well as

the lateral force curve F(x(∆

)) can be calculated as described in the previous section. The lateral force

curve is equivalent to the force vs. distance curve described above and is the experimental curve which

is measured as the tip scans over the surface. Four of these curves are shown in Figure 6.32 for different

values of c/E

· k

. The solid lines represent the forward scan, the dotted curve the backward scan. As in

the case of a force vs. distance curve, the area enclosed by these lateral force curves corresponds to the

energy dissipated during one scan cycle. As the ratio c/E

· k

decreases, the dissipated energy increases

and the lateral force curves look increasingly sawtooth-like with the typical stick-slip behavior observed

experimentally. For low values of c/E

· k

the lateral force curve can be described by a curve which is

determined by the lattice spacing l, a maximum force F

, and a force jump ∆F. For this type of curve,

the energy dissipated can be calculated using simple geometric arguments as

(6.28)

where n is the number of stick-slip processes, and the corresponding mean friction force is

The factor ½ takes account of the fact that the energy given in Equation 6.28 is due to a whole scan cycle,

while the friction force is only half the mean total height of the friction loop. Equation 6.28 can be shown

to follow also from the relation describing the energy dissipation of a general lateral force curve (Colchero

et al., 1996b).

6.4.3.4 Two-Dimensional Stick-Slip

The modeling of an SFFM setup above has been restricted to one dimension. However, experimentally

a two-dimensional stick-slip motion is observed (see Section 6.3.1.2). Therefore, in this section the model

described above will be generalized to a real two-dimensional surface (Gyalog et al., 1995). A schematic

view of the corresponding SFFM setup is shown in Figure 6.33, together with a typical lateral force curve.

In analogy with the one-dimensional model, the tip–sample position is described by a vector X = (x, y)

and the separation between the rigid support of the cantilever and the surface by a vector ∆ = (∆

, ∆

The surface potential is a periodic function V

surf

(X) in the x- and y-direction and describes the atomic

FIGURE 6.32 Calculated lateral force curve F(∆) — also called friction loop — for different values of the ratio γ =

c/E

(see text). For each curve, the lateral force is plotted vs. the (lateral) displacement ∆ of the tip. Top: γ = 1.25

(left) and γ = π/2 (right); bottom: γ = π (left) and γ = 4.5 (right). Note the stick-slip-like behavior for high values

of γ. (From reference Colchero, J. et al. (1996), Tribol. Lett. 2, 327–343. With permission.)

Enl F F=⋅⋅ −

()

∆ ,

fric

∂

=−

∆ .

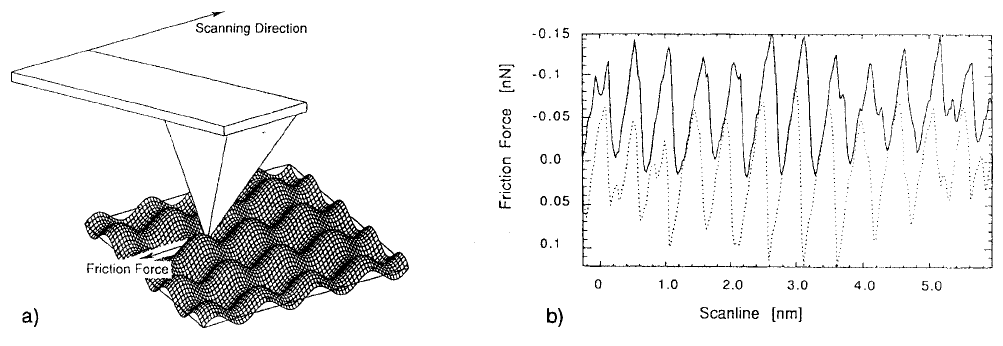
FIGURE 6.33 Schematic setup of an SFFM scanning a two-dimensional surface and a typical lateral force curve. (From Gyalog, T. et al. (1995),

Europhys. Lett. 31(5–6), 269–274. With permission.)

corrugation of the surface. The elastic energy stored in the system is determined by an elasticity matrix

(see Section 6.2.1.1) and is

where X–∆ is the deﬂection of the tip from its zero-force position. This relation is the generalization of

Equation 6.27 for a one-dimensional harmonic potential. The total energy of the tip–sample system is

tot

(X, ∆) = V

surf

(X) + V

(X, ∆). For a ﬁxed separation ∆, the tip can minimize its energy by varying

the tip–sample position X. The corresponding two-dimensional equilibrium and stability conditions are

where the numbers λ

1,2

are the eigenvalues of the Hessian matrix H

= ∂

tot

/∂x

∂x

. From the equilibrium

condition, the separation

(6.29)

as a function of the tip–sample distance X is determined. However, since the separation ∆ and not the

position X is controlled experimentally, the function X(∆) is needed to specify the behavior of the

tip–sample contact. If the surface potential is sufﬁciently corrugated, the function ∆(X) has the same

value for different X values; therefore, the inverse function X(∆) is not well deﬁned. Physically, this means

that the tip can be in more than one position for a given separation ∆. As in the one-dimensional case,

the exact conﬁguration of the tip–sample contact is determined by the history of the system, which leads

to hysteresis of the lateral force curve and to energy dissipation. To characterize the two-dimensional

stick-slip motion of the tip, the areas (x, y) of the surface, as well as the separations (∆

, ∆

) which

correspond to instable positions, have to be determined. These positions (x, y) on the surface are given

by all the points where the Hessian matrix H

has a nonpositive eigenvalue. The borders of these areas

form closed curves in the (x, y)-plane. To determine the separations where the tip jumps, these curves

are imaged into the (∆

, ∆

)-plane by applying Equation 6.29. The corresponding curves in the (∆

, ∆

plane are again closed curves, so-called critical curves. A scanning path is described by a line in the (∆

∆

)-plane. If this line crosses such a critical curve, the system becomes unstable and jumps into a new

(tip–sample) position. These critical curves are shown in Figure 6.34 for a hard and soft spring (top) in

the case of isotropic support (

C = c · Î), as well as for a hard and soft spring (bottom) in the case of

asymmetric support. For soft springs, the areas enclosed by the critical curves overlap; then all paths

show friction, and slip motion occurs when the critical curves are crossed. For hard springs, the areas

enclosed by the critical curves do not overlap. Then paths exists with and without friction.

The lateral force curve is obtained from the computed equilibrium position X(∆) as in the one-

dimensional case:

At points ∆

on the critical curve, the tip–sample contact is not stable and moves into the next stable

minimum which is found by following the curve of steepest descent on the potential surface V

tot

(X, ∆

After the excess energy has been damped, the tip–sample contact is in this nearest minimum and continues

to evolve along the curve until the next critical curve is crossed.

In conclusion, this two-dimensional stick-slip model generalizes the one-dimensional model discussed

earlier and explains all features of the observed two-dimensional lateral force curves.

XXCX,

,∆∆∆∆∆∆

()

=−

()

−

()

∇

()

=⇔∇

()

=−

()

≥

XXCXVV

tot surf

∆∆∆∆0

∆∆ XXC X

()

=− ∇

()

−

o V

surf

FX C X∆∆∆∆∆∆

()

−

()