Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

Now, substituting r 5 500 ft and dr /dt 5 2 ft/min into this last equation, gives

5 π  1000 ft 2

min

5 2000π

min

Therefore the surface area of the oil slick is increasing at the rate of 2000π square

feet per minute.

INSIGHT

Example 6 poses a question about the rate of change of A with respect to

t. The answer therefore requires the derivative of A with respect to t. Because the

formula for A, namely πr

, involves r, not t, the Chain Rule must be applied to effect the

correct differentiation. Leibniz notation aids in keeping track of the terms.

A LOOK FORWARD c When two variables are related by an equation, and one

variable changes, then the other variable must change in order to satisfy the

equation. The task of determining the unknown rate of change of one variab le from

the known rate of change of the other, as in Example 6, is called a related rates

problem. In Section 4.1 we will examine this application of differentiation in

greater detail.

Derivatives of

Exponential Functions

In Section 3.4 we learned the derivative of the natural exponential function. Now

we use that formula together with the Chain Rule to calculate the derivative of an

exponential function with an arbitrary base.

THEOREM 2

Suppose that a is a positive constant. Then

5 a

 lnðaÞ: ð3:5:6Þ

Proof. Because

the range of the natural exponential is the entire real line, there is,

for every x, a number u such that

5 a

If we apply the natural logarithm to both sides, then we obtain u 5 ln(e

) 5

ln (a

) 5 x  ln (a). In other words,

5 e

x lnðaÞ

We differentiate each side of this equation with respect to x and apply the Chain

Rule to obtain

ða

Þ5

xlnðaÞ



5 e



5 e

xlnðaÞ





x  lnðaÞ



5 e

xlnðaÞ

 lnðaÞ5 a

 lnðaÞ:

’

3.5 The Chain Rule 215

INSIGHT

Notice that Theorem 2 generalizes our earlier formula for the derivative

of the natural exponential function: when a is taken to be e, the factor ln (a) becomes

ln (e), which is 1, and formula (3.5.6) reduces to (3.4.7). This gain in simplicity is one

reason that e is the preferred base for the exponential function in calculus.

The proof of Theorem 2 employs a formula that is important in its own right. The

equation

5 e

x lnðaÞ

ð3:5:7Þ

tells us that we can always rewrite an exponential function so that e becomes the base.

⁄ EXAMPLE 7 Calculate

and

sinðxÞ

Solution For

the ﬁrst problem, we use formula (3.5.6) with a 5 3:

5 3

 lnð3Þ:

For the second problem, we set u 5 sin (x) and use the Chain Rule before we apply

formula (3.5.6) with a 5 5:

sinðxÞ



u 5 lnð 5 Þ5



sinðxÞ5 lnð5Þ5

sinðxÞ

 cosðxÞ: ¥

Summary of Derivatives of Basic Functions

ðx

Þ 5 px

p21

2 N , p , N

sinðxÞ 5 cosðxÞ

cosðxÞ 52sinðxÞ

tanðxÞ 5 sec

ðxÞ

cotðxÞ 52csc

ðxÞ

secðxÞ 5 sec ðxÞtanðxÞ

cscðxÞ 52cscðxÞcot ðxÞ

5 e

5 a

 lnðaÞ

216 Chapter 3 The Derivative

QUICK QUIZ

1. If y 5 u

, and u 5 x

1 3x 1 1, then what is dy/ dx ?

2. If g(u) 5 sin (u), and f (x) 5 3x

, then what is (g 3 f )

(x)?

3. Evaluate

4. If f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 7

; then what is f

(3)?

Answers

1. 4(x

1 3x 1 1)

(2x 1 3) 2. 15x

cos (3x

)3.3 2

ln (2) 4. 3/4

EXERCISES

Problems for Practice

c In Exercises 118, calculate the derivative of the given

expression with respect to x. b

1. sin

(3x)

2. cos (2x 1 π/3)

3. e

4. sec (x/4)

5. cos (1/x)

6. sinð

ﬃﬃﬃ

7. sin (x

1 3x)

8. tan (sin (x))

9. sec (cos (x))

10. cot (52x

)

11. tan (1 2 7x)

12. tan (x

)

13. x=

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 x

14. x

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 3x

15. cot (x

1 4) 1 csc (x

1 4)

16. exp(x

1 1)

17. exp(21/x

)

18. x

sin (1/x

)

c In Exercises 1926, use the Chain RulePower

Rule to

differentiate the given expression with respect to x. b

19. (2x 1 sin

(x))

20. (x

1 3x)

21.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

4 1 x

22. 1/tan

(x)

23. sin

(x)

24. (x 2 1/x)

5/2

25. 12

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 e

26.



x11



c In each of Exercises 2730, compute ( f 3 g)

and (g 3 f )

. b

27. f ðxÞ5 x

1 7x

; gðxÞ5

ﬃﬃﬃ

28. f (x) 5 3x

2 2x

, g(x) 5 sin (x)

29. f (x) 5 x/(x 1 1), g(x) 5 x

30. f (x) 5 sin (x), g(x) 5 3x

c In Exercises 3140, calculate the derivative of the given

expression with respect to x. b

31. 2

32. (1/3)

33. 3

34. 5

22x

35. 8

36. 3

ðx

37. (1 1 e)

1/x

38. sin (π

)

39. (3x 1 2) /5

40. 10

2

10x

c In each of Exercises 4144, use the speciﬁed value of c and

the given information about f and g to compute (g 3 f )

(c). b

41. g(3) 5 2, g

(2) 5 3, g

(3) 5 4, f (2) 5 3, f

(2) 5 8, f

(3) 5 5,

c 5 2

42. g(9) 522, g

(22) 5 7, g

(9) 523, f (22) 5 9, f

(22) 5 4,

(9) 5 5, c 522

43. g(1/2) 5 6, g

(1/2) 5 1/3, g

(6) 523, f (6) 5 1/2, f

(1/2) 5 9,

(6) 5 12, c 5 6

44. g(25)526, g

(26) 5 12, g

(25) 527, f (26) 525,

(25) 5 1/3, f

(26)529, c526

c In each of Exercises 4550 use the Chain Rule repeatedly

determine the derivative with respect to x of the given

expression. b

45.

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

1 1 ð112xÞ

46. sin (cos (3x))

47. cos

(2x)

48. (1 1 cos

(x))

3/2

49. 2 tanð

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

3x 1 2

50. ðx1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃ

12x

Further Theory and Practice

c In Exercises 5154, let c 5 4, F (x) 5 1 1 3x, G(x) 5

ﬃﬃﬃ

and H(x) 5 x/(x 1 5). Calculate the requested derivative. b

51. (F 3 G 3 H)

(c)

3.5 The Chain Rule 217

52.

F 3



cðÞ

53. (G 3 F 3 F)

(c)

54.

F 3

H 3 G



cÞð

c The basic “dimensions” of mechanics are length, mass, and

time.

Trigonometric functions are unitless because they

represent the ratio of two lengths—the units cancel. Argu-

ments of trigonometric functions are angles and so unitless.

Likewise, exponential functions are unitless and take unitless

arguments. Exercises 5558 are concerned with dimensional

analysis. b

55. An

oscillation about equilibrium is given by x(t) 5

A sin (ωt) when t is measured in seconds and x in meters.

What units do the constants A and ω bear? Use the Chain

Rule to explain why x

(t) is dimensionally correct.

56. Suppose that t represents time, y distance. If we change

the units of either t or y 5 f (t) or both, then we

change the numerical value of dy/dt. For example, 60

miles per hour is the same speed as 88 feet per second.

Explain how the Chain Rule accounts for the numerical

change in dy/dt when we change the units of y and t.

57. An object oscillates about its equilibrium position

according to the formula

xtÞ5 Ae

2kt

sinðwtÞ



when t is measured in seconds and x in centimeters.

Describe the units of the positive constants K, A, and ω.

Use the Chain Rule to explain why x

(t) is dimensionally

correct.

58. According to the Theory of Relativity, the mass m of an

object at speed υ is given by

mðυÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 2 v

where c is the speed of light, and m

is its rest mass. There

is a function ϕ such that

ðυÞ5 m

ϕðυÞ





23=2

Whatare the dimensions of m

(υ), ϕ (υ), and (1 2 υ

)

23/2

Calculate m

(υ), identifying each application of the Chain

Rule. What is ϕ(υ)? Verify that ϕ(υ) has the expected

dimensions.

59. At time t . 0whent is measured in years, the mass of a

100 g sample of the isotope

Cism(t) 5 100 e

20.001213 t

Calculate m

(t)/m(t), lim

t-N

ðtÞ,andlim

t-N

ðtÞ:

60. The diameter of a certain spherical balloon is decreasing at

the rate of 2 inches per second. How fast is the volume of

the balloon decreasing when the diameter is 8 feet?

61. The leg of an isosceles right triangle increases at the rate

of 2 inches per minute. At the moment when the hypo-

tenuse is 8 inches, how fast is the area changing?

62. If f is a differentiable function that never takes the value

0, deﬁne g( x) 5 1/f (1/x) for x 6¼0. Compute g

(x).

63. Suppose that f is a differentiable function. Let g(t) 5 f (t

Simplify f

) 2 g

(t) and f

(t) 2g

ﬃﬃ

Þ:

64. The formulas for ( f 3 g)

product of the derivatives of f and g. In what way do the

formulas differ?

c In Exercises 6574, ﬁnd f

(x) for the given function f. b

65. f (x) 5 4

sec

ﬃﬃﬃﬃﬃ

66. f (x) 5 tan (sin (e

)))

67. f (x) 5 2 tanð

ﬃﬃﬃ

Þ1 6

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

tanðxÞ

68. f (x) 5 1=

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

exp ðcos ð2xÞÞ

69. f (x) 5 (5x

11)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1

70. f ðxÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

sin

ð3xÞ1 cos

ð3xÞ

71. f (x) 5 sin

( π sin (π x

))

72. f (x) 5 cos

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 3

73. f ðxÞ5 6

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2x 2 1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

2x 1 1

74. f (x) 5 (2x

1 1)

1/3

(3x

1 1)

4/3

75. Suppose that f ðxÞ5

ðcx11Þ

if x # 0

x 1 1ifx . 0



Can we

choose c so that f is a differentiable function? If yes, then

specify c. Otherwise, explain why not.

76. Suppose that f ðxÞ5

if x # 0

1 1 sinðbxÞ if x . 0



How must

we choose a and b so that f is a differentiable function?

77. Suppose that the size P(t) of a population at time t is

PðtÞ5

1 ðM 2 P

Þe

2kMt

for some positive constants K, P

, and M . P

. (This

growth model is known as logistic growth.

a. What is the initial population size? What is the lim-

iting size of the population as t-N?

b. Verify that P

ðtÞ5 kPðtÞðM 2 PðtÞÞ.

78. If a unit mass is dropped from a height, and if the air

resistance is proportional to the velocity υ(t) of that

object, then

υðtÞ5 kgð1 2 e

2t=k

in the downward direction.

a. What is the limiting (or terminal) velocity υ

t -N?

b. Calculate the acceleration υ

(t) of the object.

c. What is the limit of the acceleration (rate of change of

velocity) as t -N?

79. If a unit mass is dropped from a height, and if the air

resistance is proportional to the square of the velocity

υ(t) of that object, then

υðtÞ5

ﬃﬃﬃ



1 2 exp ð22t

ﬃﬃﬃﬃﬃﬃ

gκ

1 1 exp ð22t

ﬃﬃﬃﬃﬃﬃ

gκ



218 Chapter 3 The Derivative

in the downward direction. Here κ is a positive constant

that depends on the aerodynamic properties of the object

as well as the density of the air.

a. What is the limiting (or terminal) velocity υ

as t-N?

b. Calculate the acceleration υ

(t) of the object.

c. What is the limit of the acceleration as t -N?

d. Verify that υ satisﬁes the differential equation

ðtÞ5 g 2 kυ

ðtÞ:

80. A drug is intravenously introduced into a patient’s

bloodstream at a constant rate beginning at t 5 0. The

concentration C of the drug in the patient’s body is given

by the formula

CðtÞ5

ð1 2 e

2βt

where α and β are positive constants.

a. Verify that C(t) is a solution of the differential

equation

ðtÞ5 α 2 β  CðtÞ :

b. Use the differential equation to deduce the rate at

which the drug is administered. How is the rate at

which the body eliminates the drug from the blood-

stream related to the concentration of the drug?

c. In the long run, what is the (approximate) con-

centration of the drug in the patient’s bloodstream?

81. The hyperbolic sine function (sinh) and hyperbolic cosine

function (cosh) are deﬁned in Exercise 72, Section 3.4.

Let a be a constant. Express

cosh (ax) and

sinh (ax)

in terms of sinh (ax) and cosh (ax).

82. The hyperbolic tangent function (tanh) and hyperbolic

cosine function (sech) are deﬁned in Exercise 73, Sec-

tion 3.4. Let a be a constant. Express

tanh (ax) and

sech (ax) in terms of tanh (ax) and sech (ax).

83. The hyperbolic tangent function (tanh) is deﬁned in

Exercise 73, Section 3.4. Verify that υðtÞ5

ﬃﬃ

tanhðt

ﬃﬃﬃﬃﬃﬃ

gκ

satisﬁes the differential equation, υ

(t) 5 g2κυ

(t). (See

Exercise 79 for the signiﬁcance of this differential

equation.)

Computer/Calculator Exercises

84. Let f (x) 5 tan (x

1 x 1 1). To ﬁve decimal places, ﬁnd

the unique value of x

in (0, 0.45) for which f

) 5 20.

85. Suppose that g(x) 5 (x 2 1)/(1 1 x

) and f (x) 5 (x 2 2)/

(1 1 x

) for x in the interval I 5 [0, 2]. Calculate g

(x),

(x), and (g 3 f )

(x). Where are g, f, and g 3 f increasing

most rapidly? (The maximum rate of increase of g 3 f does

not, in general, occur where either g or f attains its

maximum rate of increase.)

86. The average temperature in degrees Fahrenheit of the

town of Rainy Lake is modeled by

Fð tÞ5 47 2 43 cos



2π

365

ðt 2 33Þ



In this expression, t is measured in days with t 5 0 corre-

sponding to the start of the new year. On what day is

the average temperature the greatest? On what days is the

average temperature increasing the fastest? Decreasing

the fastest? Stable? What are the net temperature changes

on the days during which the temperature is stable?

87. One gram of the isotope

238

U decreases according to the

exponential decay law m(t) 5 e

2kt

g. After 4.51 billion

years, 0.5 g remains. Approximately what is the rate of

change of this

238

U sample when its mass is 1/8 g?

88. Refer to Exercise 59 for the mass of a sample of the

isotope

C that is initially 100 g.

a. When does the mass decrease at the rate of 1 gram per

millennium? (A millennium is 1000 years).

b. In which 1000-year interval, expressed in the form

, t

1 1000], is the mass reduced by exactly 1 gram?

89. A casserole dish at temperature T

5 350



F is plunged

into a large basin of hot water whose temperature is

5 115



F. The temperature of the dish satisﬁes New-

ton’s Law of Cooling:

TðtÞ5 T

1 ðT

2 T

Þe

2kt

In 25 seconds, the temperature of the dish is 175



a. Graph the temperature T.

b. Graph the rate T

at which the temperature decreases.

c. What is the rate of change of T when T is equal to

175



F? 155



F? 135



F? 125



F? 115.5



90. Two ceramic objects are removed from a T

5 450



Foven

into a room at T

5 72



F. They are to be glued together,

but the glue is not reliable when applied to objects whose

temperatures are greater than 85



F. Five minutes after

being taken from the oven, the temperature T of the

ceramic objects is 300



F. Refer to the preceding exercise

for Newton’s Law of Cooling. Graph the temperature T.

Graph the rate T

at which the temperature decreases.

What is the rate of change of T when the objects are cool

enough to be glued? If the thermometer used is accurate

to three signiﬁcant digits, when are the objects at 75



91. After jumping from an airplane, a skydiver has velocity

given by

υðtÞ52256ð1 2 e

2t=8

Þ ft=s:

Eight seconds into her descent, she opens her parachute.

For t $ 8, her velocity is given by

υðtÞ5216 2 ð240e 2 256Þe

22t115

ft=s:

Graph υ(t). Is it everywhere continuous? Differentiable?

Graph υ

(t) (the acceleration). Is it everywhere con-

tinuous? Differentiable?

3.5 The Chain Rule 219

3.6 Derivatives of Inverse Functions

The Sum Rule, Product Rule, Quotient Rule, and Chain Rule are essential tools in

the theory of differentiation. The key idea behind them is that the differentiation of

a complicated function can be reduced to calculating the derivatives of its basic

building blocks. Thus we have learned how to obtai n the derivatives ( f 1 g)

,(f g)

( f / g)

, and (g 3 f )

from the derivatives f

and g

. In this section, we continue this

program by developing a formula that expresses the derivative of an inverse

function f

in terms of the derivative of f. As an important application of this

theory, we consider the function f (x) 5 e

and its inverse function f

(x) 5 ln(x )in

detail and obtain information about the derivative of the logarithm function.

Continuity and

Differentiability of

Inverse Functions

Suppose that S and T are open intervals and that f : S-T is an invertible function.

This means that, for every t in T, there is exactly one s in S such that f (s) 5 t.

Equivalently, there is a function f

: T - S such that f ( f

(t)) 5 t for all t in T, and

( f (s)) 5 s for all s in S. Our immediate goal is to ﬁnd a relationship between

( f

)

and f

. A simple example illustrates what we have in mind.

⁄ EX

AMPLE 1 Let S 5 (0, N), T 5 (9,N), and let f : S-T be deﬁned by

f (s) 5 s

1 9. Calculate ( f

)

(25).

Solution Setting t 5 s

1 9, we ﬁnd

s 5

ﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃﬃ

t 2 9

; ð3:6:1Þ

which tells us that f

(t) 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

t 2 9:

We calculate ( f

)

(t) by using the Chain

RulePower Rule:

ðtÞ5

ðt2 9 Þ

21=2

ðt 2 9Þ5

ðt2 9 Þ

21=2

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

t 2 9

: ð3:6:2Þ

Therefore

ðf

ð25Þ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

25 2 9

: ¥

INSIGHT

The solution of Example 1 relies on an explicit formula for f

(t). This

method has a serious drawback: It is not always possible to ﬁnd a formula for an inverse

function. Notice, however, that if equation (3.6.1) is used to simplify equation (3.6.2),

then we obtain

ðtÞ5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

t 2 9

Looking for a relationship between ( f

)

and f

, we calculate

ðsÞ5

ðs

1 9Þ5 2s

and notice that this expression is the denominator of our formula for f

(t). That is,

ðtÞ5

f ðsÞ

220 Chapter 3 The Derivative

Observe that, with this equation, we do not need a formula for f

(t) because the right-

hand side does not involve f

(t). It is precisely this relationship between ( f

)

(t) and

(s) that we will now examine in greater generality.

Before seeking a formula for ( f

)

(t), it is appropriate that we ﬁrst investigate

when the limit that deﬁnes the derivative exists. Our next theorem states a con-

dition that guarantees the differentiability of f

THEOREM 1

Suppose that S and T are open real intervals and that f : S - T is

invertible.

(a) If f is continuous on S, then f

is continuous on T.

(b) If f is differentiable on S and f

is never zero on S, then f

differentiable on T.

Proof. We

will sketch a pro of of part (b), which is our primary interest in this

section. Let c be a point in S, and set γ 5 f (c). Supposing that f

ðcÞ exists, and f

ðcÞ6¼

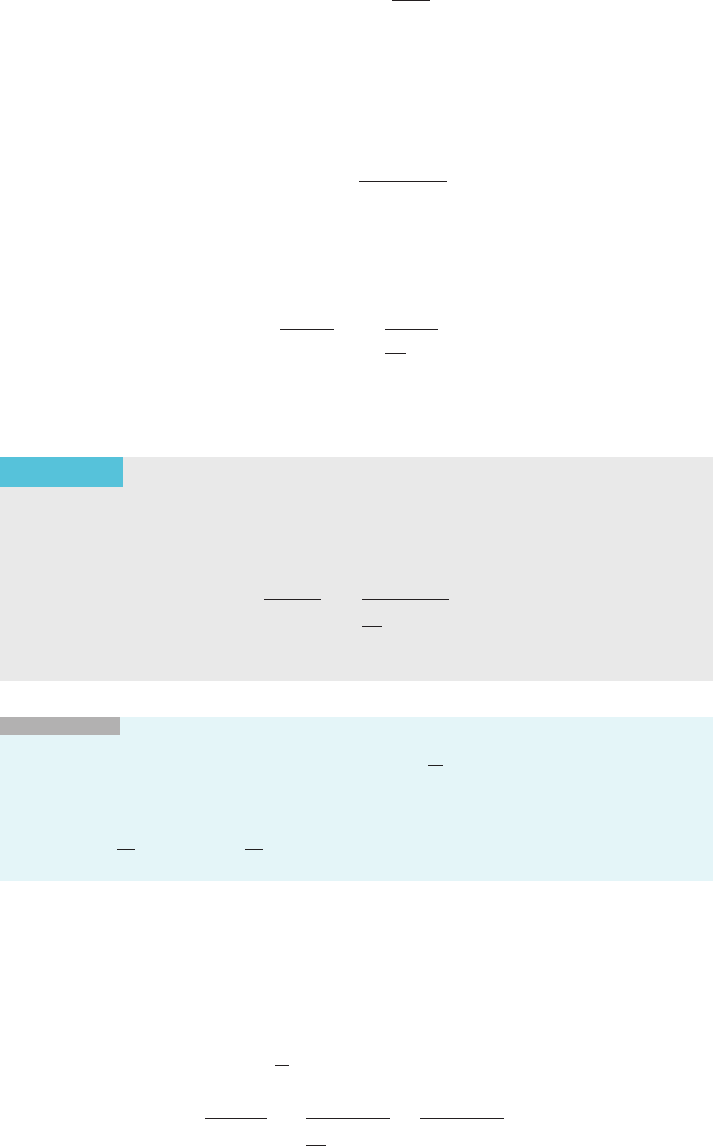
0, we infer that the graph of f has a nonhorizontal tangent line ‘ at (c, γ ). See

Figure 1. In Section 1.5 we learned that the graph of f

: T- S is the reﬂection of

the graph of f through the line y 5 x. In this reﬂection through y 5 x, the

nonhorizontal line ‘ is transformed to a nonvertical tangent line L to the graph of

at (γ, c). See Figure 2. This is precisely the geometric criterion for the existence

of the derivative of f

at γ. ’

The relationship between the graphs of f an

d f

also allows us to deduce the

value of ( f

)

(γ). Reﬂection through the line y 5 x has the effect of inte rchanging

x and y coordinates. Therefore if Δy/Δx is the slope of line ‘, then Δx/Δy is

the slope of the reﬂected line L. See Figure 3. In other words, the slope of L is the

reciprocal of the slope of ‘. Because f

ðcÞ is the slope of ‘, it follows that L must

have slope 1/f

ðcÞ. That is,

y  x

(c, )

  f(c)

m Figure 1

y  x

1

(c, )

(, c)



  f(c)

m Figure 2

y  x

1

(c, γ)

(γ, c)

Δ x

Δ y

γ  f(c)

Δ x

Δ y

slope L 

Δ y

Δ x

slope ᐍ 

ᐍ

m Figure 3

3.6 Derivatives of Inverse Functions 221

ðf

ðγÞ5

ðcÞ

ð3:6:3Þ

where c and γ are related by the equations γ 5 f ( c) and c 5 f

(γ).

Let us use calc ulus to verify our deduction. To begin, we differentiate both

sides of the basic equation ( f 3 f

)(t) 5 t with respect to t. Notice that we will have

to use the Chain Rule on the left side. We get f

( f

(t)) ( f

)

(t) 5 1or

ðf

ðtÞ5



ðtÞ



: ð3:6:4Þ

Notice that equation (3.6.4) validates our geometric argument: when we set t 5 γ in

equation (3.6.4) and remember that c 5 f

(γ), we obtain equation (3.6.3). If we let

s 5 f

(t), then we can write formula (3.6.4) in Leibniz notation as

dðf

1

ðtÞ5

ðsÞ:

We now have an equation for the derivative of the inverse of a function. We

summarize it in the following theorem:

THEOREM 2

The Inverse Function Derivative Rule Let f be an invertible

function that is deﬁned on an open interval containing the point s. Let t 5 f (s). If

f is differentiable at s 5 f

(t) and if df/ds is nonzero at this point, then the

derivative of f

at t is given by

dðf

1



s5f

1

ðtÞ:

ð3:6:5Þ

INSIGHT

This new formula brings to mind one feature of the Chain Rule: We must

keep careful track of where we should be evaluating

: We should evaluate this

derivative at the same place where we evaluate f

, which would be at an element t in T.

But then s 5 f

(t) is the corresponding element of S, and that is where we should

evaluate f or

: That is why

appears in formula (3.6.5) with the argument f

(t).

⁄ EXAMPLE 2 Let f (s) 5 s

. Use the Inverse Function Derivative Rule to

calculate ( f

)

(t). Verify your work by ﬁnding a formula for f

(t) and then

differentiating f

(t) directly.

Solution When

we use the Inverse Function Derivative Rule to calculate ( f

)

(t),

we ﬁrst calculate f

(s). In this exampl e, we have f

(s) 5 3s

. The Inverse Function

Derivative Rule tells us that if

s5f

ðtÞ

6¼ 0; then

dðf 21Þ



s5f

ðtÞ

s5f

ðtÞ

222 Chapter 3 The Derivative

Now, if s 5 f

(t), then t 5 f (s) 5 s

. Solving this equation for s, we obtain s 5 t

1/3

,or

(t) 5 t

1/3

. Thus

dðf



3ðt

1=3

22=3

for t 6¼ 0:

To verify this formula for ( f

)

(t), we can apply the Power Rule directly to

(t), which we hav e already found. We obtain

ðf

ðtÞ5

1=3

1=321

22=3

for t 6¼ 0;

which agrees with the formula we derived from the Inverse Function Derivative

Rule.

⁄ EXAMPLE 3 The function f (x) 5 (x

1 x 1 2)

5/2

is increasing and therefore

invertible. Calculate ( f

)

(32).

Solution In

this example, we cannot compute an explicit formula for f

. However,

the Inverse Function Derivative Rule—in the form of equation (3.6.3)—tells us that

( f

)

(32) 5 1/f

ðcÞ where c is the unique number such that f (c) 5 32, or

1 c 1 2)

5/2

5 32. Raising each side to the 2/5

power, we obtain c

1 c 1 2 5 4. In

this case, we can spot that c 5 1. Using the Chain RulePower Rule, we calcu late

ðxÞ5

ðx

1x12Þ

3=2

ð5x

1 1Þð3:6:6Þ

and therefore

ðcÞ5 f

ð1Þ5

ð1

1112Þ

3=2

ð5  1

1 1Þ5 120:

We conclude that ( f

)

(32) 5 1/f

ðcÞ5 1/120. ¥

INSIGHT

In Example 3, we were unable to evaluate s 5 f

(t) for a general value

of t. That inability prevented us from calculating ( f

)

(t) directly—we did not have an

expression to differentiate. Instead, we applied the Inverse Function Derivative Rule. To

do so, we had to ﬁnd the value c 5 f

(γ) for γ 5 32. In other words, we had to solve the

equation s 5 f

(t) for a speciﬁc value γ of t. That value, 32, may have seemed artiﬁcial.

Indeed, it was chosen so that we could solve f (c) 5 γ by inspection. In practice, however,

other values of γ would have posed no greater difﬁculty. That is because we can turn to

the “solve” command of a calculator or computer if, for a given γ, we cannot ﬁnd an exact

solution c of the equation f (c ) 5 γ. For example, suppose that we require ( f

)

(35). The

command fsolve((x^5 1 x 1 2)^(5/2) 5 35, x) in the computer algebra system

Maple tells us that x 5 1.0234 solves the equation f (x) 5 35 (to four decimal places).

Substituting this value of x in formula (3.6.6) gives us f

(x) 5 136.86. It follows from the

Inverse Function Derivative Rule that ( f

)

(35) 1/136.86.

Derivatives of

Logarithms

The Inverse Function Derivative Rule can be used to calculate the derivative

of the logarithm functions that we studied in Section 2.6. We begin with the natural

logarithm, which is the logarithm with base e.

3.6 Derivatives of Inverse Functions 223

THEOREM 3

For every t . 0, we have

lnðt Þ5

: ð3:6:7Þ

Proof. Let f (s ) 5 e

. Then f

(t) 5 ln (t). Applying the Inverse Function Derivative

Rule, we have

dðf



s5f

ðtÞ

s5f

ðtÞ

lnðtÞ

’

⁄ EX

AMPLE 4 Find the equation of the tangent line to the graph of

y 5 ln

(x) at its x-intercept.

Solution Earlier

in this section, we observed that ln (1) 5 0. Because the natural

logarithm is an increasing function, the point (1, 0) is the only x-intercept of the

curve y 5 ln (x). Because

lnðxÞ



x51



x51

5 1;

the Point-Slope Equation for the required tangent line is y 5 1 (x 2 1) 1 0or

y 5 x 2 1. See Figure 4.

⁄ EXAMPLE 5 Calculate



ﬃﬃﬃ

secðxÞ



Solution A

glance at the argument of the logarithm may suggest that the Product

Rule is needed for the calculation. In fact, that is not the case. By applying

properties (2.6.17) and (2.6.19) of the natural logarithm prior to differentiation, we

can simplify the differentiation:



ﬃﬃﬃ

secðxÞ





lnð

ﬃﬃﬃ

Þ1 ln



secðxÞ







lnðx

1=2

Þ1 ln



secðxÞ





lnðxÞ1

lnðuÞðu 5 secðxÞÞ

lnðuÞ

secðxÞ tanðxÞ

1 tanðxÞ: ¥

123

y  x  1

y  1n(x)

1

2

3

m Figure 4

224 Chapter

3 The Derivative