Blank B.E., Krantz S.G. Calculus: Single Variable
Подождите немного. Документ загружается.


is known as a forward difference quotient. The backw ard
difference quotient is defined by
D
2
f ðc; hÞ5
f ðcÞ2 f ðc 2 hÞ
h
where h . 0. The central difference quotient is defined by
D
0
f ðc; hÞ5
f ðc 1 h=2Þ2 f ðc 2 h=2Þ
h
: ð3:3:1Þ
Each of these three difference quotients can be used to
approximate f
0
ðcÞ. However, the situation illustrated by
Figure 1 is typical: For a given value of h, the central dif-
ference quotient generally gives the best approximation to
the derivative.
When we use the approximation
D
0
f ðc; hÞf
0
ðcÞ;
the question of how to choose h in an optimal way is not easy to answer. Consider
f (x) 5 x
4
and c 5 1/2. The exact value of f
0
ðcÞ is 1/2. Now consider the following
table of difference quotients (which were computed using ten significant digits, of
which six are exhibited):
hD
1
f (c, h ) D
2
f (c, h) D
0
f (c, h)
10
21
0.671 0.369 0.505
10
22
0.505201 0.485199 0.50005
10
23
0.501502 0.498502 0.500001
10
24
0.50015 0.49985 0.5
10
26
0.500002 0.499998 0.5
10
27
0.499999 0.499999 0.500002
10
29
0.500222 0.499995 0.500222
10
211
0.500222 0.500222 0.477485
10
212
0.454747 0.500222 0
Table 1
As
you read down each column, you will notice that, with decreasing h, each
difference quotient seems to approach the limit 0.5 at first. Observe that the central
difference quotient converges quickest. In each column, howeve r, accuracy is
degraded when h becomes too small. This is the result of loss of significance,a
problem that is discussed in Section 1.1.
It is difficult to predict the value of h at which accuracy begins to deteriorate.
There are two types of error that result when we use D
0
f (c, h) to approximate f
0
ðcÞ.
c hc hc
Tangent line
Slope Central
difference
quotient
Slope Forward
difference
quotient
Slope Backward
difference
quotient
c
h
2
c
h
2
m Figure 1
3.3 Rules for Differentiation 195

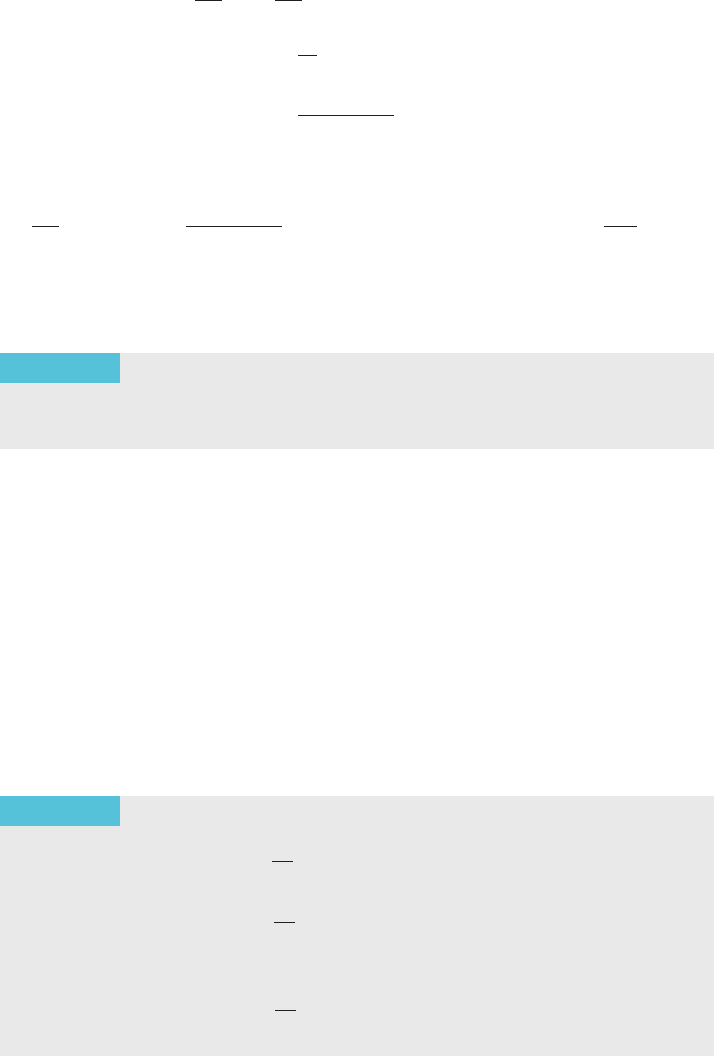
As we have seen, there is a roundoff error r(h). Terminating the limit process
f
0
ðcÞ 5 lim
h-0
D
0
f ðc; hÞ by stopping at a particular value of h also introduces a
truncation error t(h). The total error e(h)isgivenbye(h) 5 t(h) 1 r(h). Typical
graphs of these error functions can be seen in Figure 2. Unfortunately, there is no
way to ensure that t(h)andr(h)areboth very small. One strategy is to let h become
smaller and smaller until either the desired accuracy is attained or the total error
begins to increase.
⁄ EX
AMPLE 6 Let VðxÞ5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 1 sinðxÞ
p
: Approximate V
0
(0.4174) to four
significant digits.
Solution Table
2 presents the results of our central difference quotient
calculations. (Ten digits have been carried in the computations, six digits are
tabulated, but no more than four are significant.)
h 0.1 0.01 0.001 0.0001 0.00001 0.000001
D
0
V(0.4174, h) 0.294630 0.294708 0.294709 0.294710 0.294700 0.295000
Table 2
Bec
ause the leftmost four digits of D
0
V(0.4174, h) agree when h 5 10
22
and 10
23
,
we can be reasonably certain that V
0
(0.4174) 5 0.2947 to four significant digits
(and that the last column represents a decline in accuracy caused by using too small
a value for h). In Section 3.5, we will be able to show that V
0
ðxÞ5 cos ðxÞ=
2
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
2 1 sinðxÞ
p
: With this formula for V
0
(x), we can verify that our numerical
differentiation is correct to four significant digits.
¥
Summary of Differentiation Rules
Sum Rule
ðf 1 g Þ
0
ðxÞ5 f
0
ðxÞ1 g
0
ðxÞ or
d
dx
ðf 1 gÞðxÞ5
df
dx
ðxÞ1
dg
dx
ðxÞ
Difference Rule
ðf 2 gÞ
0
ðxÞ5 f
0
ðxÞ2 g
0
ðxÞ or
d
dx
ðf 2 gÞðxÞ5
df
dx
ðxÞ2
dg
dx
ðxÞ
Constant Multiple Rule
ðα f Þ
0
ðxÞ5 α ðf
0
ðxÞÞ or
d
dx
ðα f ÞðxÞ5 α
df
dx
ðxÞ
Constant Rule
ðαÞ
0
5 0or
d
dx
α 5 0ifα is any constant
Product Rule
ðf gÞ
0
ðxÞ5 f
0
ðxÞgðxÞ1 f ðxÞg
0
ðxÞ or
d
dx
ðf gÞðxÞ5
df
dx
ðxÞ
gðxÞ1 f ð x Þ
dg
dx
ðxÞ
Quotient Rule
f
g
0
ðxÞ5
gðxÞf
0
ðxÞ2 f ðxÞg
0
ðxÞ
gðxÞ
2
or
d
dx
f
g
ðxÞ5
gðxÞ
df
dx
ðxÞ2 f ðxÞ
dg
dx
ðxÞ
gðxÞ
2
h
e
e(h) t(h) r(h)
r(h)
t(h)
m Figure 2
196 Chapter
3 The Derivative

Reciprocal Rule
1
g
0
ðxÞ52
g
0
ðxÞ
gðxÞ
2
or
d
dx
1
g
ðxÞ52
dg
dx
ðxÞ
gðxÞ
2
Approximate Derivative Rule
f
0
ðcÞ
f ðc 1 h=2Þ2 f ð c 2 h=2Þ
h
Derivatives of Basic Functions
d
dx
ðx
n
Þ 5 nx
n21
for n 521; 0; 1; 2; 3
d
dx
sinðxÞ 5 cosðxÞ
d
dx
cosðxÞ 52sinðxÞ
d
dx
secðxÞ 5 secðxÞtanðxÞ
QUICK QUIZ
1. What is the derivative of x sin (x)?
2. What is the derivative of cos (x)/x?
3. What is the derivative of sec (x)?
4. Use the central difference quotient with h 5 0.1 to app roximate the derivative of
tan (x)atx 5 0.
Answers
1. sin (x) 1xcos
(x)2.2(x sin (x ) 1 cos (x))/x
2
3. sec (x) tan (x) 4. 1.00083
EXERCISES
Problems for Practice
c In Exercises 16, use the rules for differentiating sums and
differences, as in Example 1, to compute the derivative of the
given expression with respect to x. b
1. 5x
3
2 3x
2
1 9
2. 6 2 4/x 1 4x2x
2
/2 2 2x
3
3. x
3
/π 1 π cos (x) 1
ffiffiffi
π
p
4. 3x
3
2 2x
2
1π sin (x) 1 1/π
5.
1
5
ð4sinðxÞ2 3cosðxÞÞ1 5x
6.
ffiffiffi
2
p
ðsinðxÞ2 2cosðxÞÞ1 2x
2
2 3=x
c In Exercises 718, use the Product Rule to compute the
derivative
of the given expression with respect to x. (In each
of Exercises 7, 8, 14, 16, and 18, do not avoid using the
Product Rule by first expanding the product.) b
7. x
2
(x 1 3)
8. 4x(x
2
1 5)
9. x
3
cos (x)
10. 5 sin (x) 2 6x cos ( x)
11. sin
2
(x)
12. cos
2
(x)
13. sin (x) cos (x)
14. (x
2
2 5)(3x 1 2)
15. 7(x
2
1 x) sin (x)
16. 3x
3
(x
3
1 7)
17. (1/x) sin (x)
18. (1/x) (5x
3
1 4/x)
c In Exercises 1926, use the Reciprocal Rule to compute
the
derivative of the given expression with respect to x. b
19. 1/(x 1 1)
20. 1/(11x
2
)
21. 2/(3x
2
1 4)
22. 3/(2 1 sin (x))
23. 1/(x 1 3 cos (x))
24. 5/(cos (x) 1 sin (x))
25. 9/(3 cos (x) 1 x
3
)
26. 1/(x
3
1x
2
1 1)
3.3 Rules for Differentiation 197

c In Exercises 2738, use the Quotient Rule to compute the
derivative of the given expression with respect to x. b
27. x/(x 1 1)
28. 3x/(x
2
1 1)
29. (x 2 1)/(x 1 1)
30. (x
2
1 1)/(x
2
1 2)
31. (5x 2 2/x)/x
32. x/sin (x)
33. sin (x)/x
34. cos (x)/(x 2 5)
35. (x
2
1 7)/cos (x)
36. 2x
3
/(1 1 cos (x))
37. (1 2 cos (x))/(1 1 cos (x))
38. (x 1 sin (x))/(x 1 cos (x))
c Calculate the derivative of each of the expressions in
Exercises 3944 by applying both the Product and Quotient
Rules. b
39. x sin
(x)/(x 1 1)
40. x cos (x)/(x
2
1 3)
41. x (x
2
1 1) (x
3
1 2)
42. sin
2
(x)/x
43. sin
2
(x) sec (x)
44. x sin (x)/(x 1 sin (x))
c In Exercises 4550, find the tangent line to the graph of
the
given function at the given point. b
45. f (x) 5 (x 1 3)/(x 1 1), P 5 (1,
2)
46. f (x) 5 x cos (x), P 5 (π, 2π)
47. f (x) 5 6/(11x
2
), P 5 (1, 3)
48. f (x) 5 4 sin (x) cos (x), P 5 (π/4, 2)
49. f (x) 5 sin (x)/(x 1 1), P 5 (0, 0)
50. f (x) 5 (3x
2
2 5)/(x 1 4), P 5 (1, 22/5)
c In Exercises 5154, use the result of Example 4 to compute
th
e derivative of the given expression with respect to x. b
51. x sec
(x)
52. sec (x)/x
53. 1/(1 1 2 sec (x))
54. (sec (x) 2 cos (x))/sin (x)
c In Exercises 5558, use the given information to estimate
f
0
ðcÞ at the given point c. b
55. f (4) 5 5.7
and f (4.1) 5 6.2, c 5 4
56. f (4) 5 5.7 and f (4.1) 5 6.2, c 5 4.1
57. f (π 1 0.01) 5 f (π) 1 0.2, c 5 π
58. f (3.47) 5 2.61 and f (3.49) 5 2.67, c 5 3.48
Further Theory and Practice
59. Given f (2) 5 3, f
0
(2) 5 5, g(2) 5 8, and g
0
(2)526, find
( f g)
0
(2) and ( f/g)
0
(2).
60. Given f (3)524 and f
0
(3) 5 6, find (1/f )
0
(3) and ( f
2
)
0
(3).
61. Given f (21) 5 5, g(21) 5 4, f
0
(21) 5 2, and g
0
(21)528,
find ( f g)
0
(21), ( f
2
)
0
(21), and (g
2
)
0
(21).
62. Given f (4) 5 2, g(4) 5 1, f
0
(4)525, and g
0
(4)529, find
(f g
2
)
0
(4), (g f
2
)
0
(4), (1/f
2
)
0
(4), and (g/ f )
0
(4).
63. Use the Quotient Rule to differentiate
x 1 1=x
1=x
:
Verify your answer by simplifying the expression and
then differentiating.
64. Derive a formula for
d
dx
x
4
by applying the Product Rule
to x x
3
. Verify your answer by applying the Product
Rule to x
2
x
2
.
c In Exercises 6570, calculate the derivative of the given
expression. b
65. x
26
66. (x
2
1 1) (x
3
1 2) sin (x)
67. x sin (x) cos (x)
68. sin
3
(x)
69. (x
2
1 1)
3
70. sin (2x)
71. The graph of f (x) 5 2x/(x 1 1) and the point P 5 (2, 4),
which lies above the graph, are shown in Figure 3. The
purpose of this exercise is to find the equation of every
tangent line to the graph of f that passes through P. Copy
Figure 3 on your paper. To your sketch, add the tangent
lines that pass through P. How many do there appear to
be? You will use this predicted number N as a “reality
check” in part c.
a. What is the slope of the tangent line to the graph of f
at (c, f ( c))? (By inspection, the tangents to the graph
of f all slope upward. Before continuing, make sure
that your algebraic formula for the slope is consistent
with this property.)
b. What is the equation of the tangent line to the graph
of f at (c, f (c )).
c. What equation must c satisfy if the tangent line at
(c, f (c)) passes through P? (How many solutions does
this equation have? Before continuing, make sure that
the equation for c has the same number of solutions as
your predicted number N.)
4 2
2
6
4
2
2
y
2x
x 1
y
x
P
m Figure 3 The graph of f ðxÞ5
2x
x 1 1
198 Chapter 3 The Derivative

d. Find the equations of all tangent lines to the graph of f
that pass through P.
72. If f is a differentiable function, find a formula for ( f
2
)
0
(x).
Next find a formula for ( f
3
)
0
(x). What do you expect the
formula for ( f
n
)
0
(x) is? (Predict by analogy, but do not
prove this last formula. These matters will be taken up
later in the chapter.)
73. Find constants A and B such that f (x) 5 A cos (x) 1
B sin (x) satisfies
f
0
ðxÞ1 f ðxÞ5 3cosðxÞ2 5sinðxÞ:
74. Suppose that f (x) 5 (x 2 r)
3
p(x) where p(x) is a differ-
entiable function with p(r) 6¼0. Show that there is a dif-
ferentiable function q with q(r)6¼ 0 such that f
0
(x) 5
(x 2 r)
2
q(x).
75. Show that if f (x) 5 |x|, then ( f
2
)
0
(0) exists even though
f
0
(0) does not.
76. We know that
d
dx
x 5 1;
d
dx
1 5 0; and
d
dx
ff
1
ðxÞ1 1 f
n
ðxÞg5
d
dx
f
1
ðxÞ1 1
d
dx
f
n
ðxÞ:
Explain what is wrong with the following reasoning:
d
dx
x ¼
d
dx
1 þþ1
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
x summands
8
<
:
9
=
;
¼ 0 þþ0
|fflfflfflfflfflfflffl{zfflfflfflfflfflfflffl}
z
8
<
:
9
=
;
¼ 0
77. Assume that g is differentiable and nonvanishing and that
1/g is differentiable. Derive the Reciprocal Rule for g
from the Product Rule applied to g and 1/ g.
78. Show that if f (x) 5 x
2
, then the central difference quo-
tient D
0
f (c, h) for approximating f
0
ðcÞ is exactly equal to
f
0
ðcÞ.
79. Show that the central difference quotient D
0
f (c, h)isan
average of a forward and a backward difference quotient.
80. Suppose that a consumer’s satisfaction with purchasing x
units of good X and y units of good Y can be quantified.
The locus of points (x, y) for which the consumer’s satis-
faction is a fixed value is called an indifference curve: The
consumer is equally satisfied at all points on the curve.
A typical indifference curve is illustrated in Figure 4. Most
consumers have a fixed budget for the purchase of goods
X and Y. The locus of points that represent the combi-
nation of goods X and Y that the consumer can actually
purchase on his budget is a straight line called the budget
line. The point of tangency between the budget line and
an indifference curve is called the consumer equilibrium.
See Figure 4. If (2, 1/5) is the equilibrium point for a
consumer whose indifference curve is
3yðx
2
þ 1Þþ5xðy þ 1Þ¼15;
find the consumer’s budget line in the form
Ax þ By ¼ C:
81. If q( p) is the demand for a product at price p, that is, the
number of units of the product that are sold at price p,
then
EðpÞ52q
0
ðpÞ
p
qðpÞ
is defined to be the elasticity of demand.
a. Let Δp denote a small change in p, and let Δq 5
q(p 1 Δp) 2 q(p) be the corresponding change in q.
Show that, for Δp sufficiently small, we have the
approximation
EðpÞ2
Δq=qðpÞ
Δp=p
:
b. Elasticity of demand for potatoes at standard super-
market prices has been estimated to be 0.31.
Approximately what percentage change in potato
consumption will result from a 2% increase in the
price of potatoes?
c. Over a fixed period, a television repair service recor-
ded the number of repairs that it made at three dif-
ferent prices:
Price Contracts Obtained
$90 96
$80 200
$70 300
Estimate the elasticity of demand at p 5 $70 and at
p 5 $90. Use a central difference quotient to estimate
elasticity of demand at p 5 $80. (Elasticity of demand
for television repair was estimated to be 3.84 in the
1970s.)
82. Let f
n
(x) 5 x
n
for each nonnegative integer n. Notice that
f
n11
(x) 5 xf
n
(x). Use the Product Rule to show that
f
0
nþ1
ðxÞ¼f
n
ðxÞþf
0
n
ðxÞ:
Use this equation to show that f
n11
0
(x) 5 (n 1 1)x
n
if
f
n
0
(x) 5 nx
n 2 1
. In other words, if the formula
x
y
Indifference curve for
good X and good Y
Consumer equilibrium
Budget
line
m Figure 4
3.3 Rules for Differentiation 199

d
dx
x
n
5 nx
n21
is valid for a nonnegative integer n, then it is valid for the
next integer n 1 1. In fact, we know that this differ-
entiation formula is true for n 5 0, 1, 2, and 3. It follows
that the formula is true for the next integer 4. Because
the formula is true for 4, it is true for the next integer 5,
and so on. We deduce that
d
dx
x
n
5 nx
n21
for all nonnegative integers n:
Calculator/Computer Exercises
c In Exercises 8386, a function f and a point c are given.
Prepare a table of the forward, backward, and central dif-
ference quotients, D
1
f (c, h), D
2
f (c, h), D
0
f (c, h) respec-
tively, for h 5 10
2n
,1# n # 5. b
83. f (x) 5 cos
(πx), c 5 1
84. f (x) 5 sin (πx), c 5 1/4
85. f ðxÞ5
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 1=x
p
; c 5 3
86. f (x) 5 (x
3
1 3x
2
1 2) /(x
2
2 2), c 5 2
c In Exercises 8790, find f
0
ðcÞ (exactly) for the given
function f and the given value c of x. Then approximate f
0
ðcÞ
to 5 decimal places by (1) finding a floating point evaluation
of the exact answer and (2) using a central difference quotient
D
0
f (c, h). Record the value of h used. b
87. f (x) 5 sin
(x), c5 π /6
88. f ðxÞ5
ffiffiffiffiffi
2x
p
; c 5 1
89. f ðxÞ5 1=x; c 5 1=
ffiffiffi
2
4
p
90. f (x) 5 cos (x), c 5 π/4
91. Let f (x) 5 cos (x). Graph x / to D
0
f (x,10
25
) for
0 # x # 2π. What is f
0
(x)? Add the graph of f
0
(x) to your
viewing window. (The graphs should nearly coincide.)
92. Let f (x) 5 x
4
/4. Graph x/ D
0
f (x,10
25
)for21.5 # x # 1.5.
What is f
0
(x)? Add the graph of f
0
(x) to your viewing
window. (The graphs should nearly coincide.)
93. The purpose of this exercise is to locate a value a
0
such
that
d
dx
a
x
0
x50
5 1:
Let f
a
(x) 5 a
x
. Set L(a) 5 D
0
f
a
(0, 10
25
). Compute L(2.70)
and L(2.73). Graph L for 2.70 # a # 2.73 to see that there
is a value a
0
in [2.70, 2.73] such that L(a
0
) 5 1. Narrow
down the interval in which a
0
must lie until you have
found a
0
to three decimal places.
94. Let f (x) 5 sin
2
(x). Graph x / D
0
f (x,10
25
) for 0 # x #
2π. Now compute f
0
, and add the graph to the viewing
window. (The graphs should nearly coincide.)
3.4 Differentiation of Some Basic Functions
In the preceding section, we learned how to differentiate functions that are formed
arithmetically from simpler functions, provided that we know how to differentiate
the simpler ones. The purpose of this section is to build up the library of basic
functions that we can differentiate. Your work in calculus will be easier if you
commit these derivatives to memory.
Powers of x By now we have learned to differentiate x
p
for the integers p 521, 0, 1, 2, and 3.
For these values of p, we know that
d
dx
x
p
5 px
p21
: ð3:4:1Þ
In our first example, we extend equation (3.4.1) to include all positive integer
values of p.
⁄ EX
AMPLE 1 Suppose that p is a positive integer. Let f (x) 5 x
p
. Show that
f
0
ðcÞ5 pc
p21
.
Solution Because
we already know that the asserted formula is true for p 5 1, we
assume that 1 , p. Because p21 is positive, we have lim
x-0
x
p21
5 0. Thus formula
(3.2.3) with c 5 0 simplifies as follows:
200 Chapter 3 The Derivative
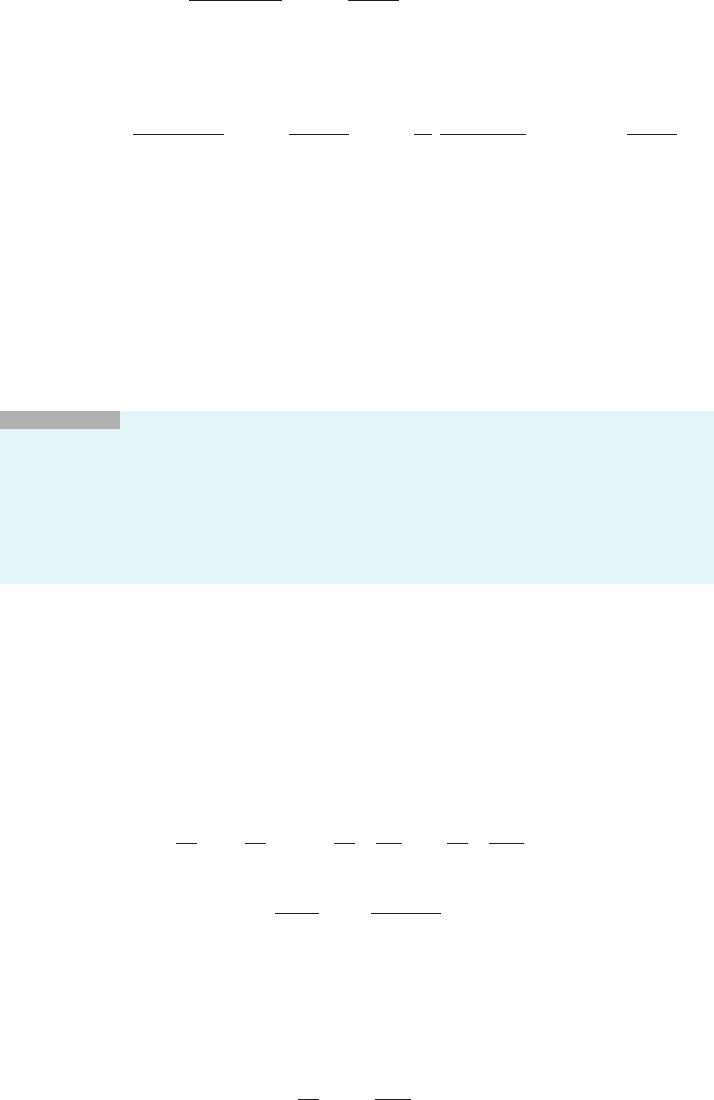
f
0
ð0Þ5 lim
x-0
f ðxÞ2 f ð0Þ
x 2 0
5 lim
x-0
x
p
2 0
x 2 0
5 lim
x-0
x
p21
5 0 5 p 0
p 21
:
Having establi shed the desired formula for c 5 0, we now assume that c 6¼0 and set
r 5 x/c. Notice that r - 1asx-c. Using formula (3.2.3), we have
f
0
ðcÞ5 lim
x-c
f ðxÞ2 f ðcÞ
x 2 c
5 lim
x-c
x
p
2 c
p
x 2 c
5 lim
x-c
c
p
c
ðx=cÞ
p
2 1
x=c 2 1
5 c
p21
lim
r-1
r
p
2 1
r 2 1
:
We now appeal to equation (2.5.2) with N 5 p to obtain
f
0
ðcÞ5 c
p21
lim
r-1
1 1 r 1 r
2
1 1 r
p21
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
p summands
0
B
B
@
1
C
C
A
5 c
p21
1 1 1 1 1
2
1 1 1
p21
|fflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl{zfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflfflffl}
p summands
0
B
B
@
1
C
C
A
5 pc
p21
: ¥
INSIGHT
Equation (3.4.1) refers to a variable x. By contrast, the derivative formula
of Example 1 was obtained by treating c as a fixed point. This choice was made to
facilitate the notation used in the solution. We should now observe that Example 1
establishes f
0
ðcÞ5 pc
p21
for every value of c. In other words, we may regard c as a
variable in the formula. With that understanding, we may replace c with the more
conventional choice of variable x. We then obtain f
0
(x) 5 px
p21
, which is precisely
equation (3.4.1) with a different choice of notation for the derivative.
We now know that equation (3.4.1) holds for all integer values of p with
21 # p. In our next example, we extend this result to all integer values of p.
⁄ EX
AMPLE 2 Use the Reciprocal Rule to show that formula (3.4.1) holds
for all integer values of p with p #22.
Solution Suppos
e that p #22. Write p 52jpj, and set g(x) 5 x
jpj
. From Example
1, we know that g
0
(x) 5 jpj x
jpj21
. Therefore using the Reciprocal Rule, we have
d
dx
x
p
5
d
dx
x
2jpj
5
d
dx
1
x
jpj
5
d
dx
1
gðxÞ
52
g
0
ðxÞ
g
2
ðxÞ
52
jpjx
jpj21
x
2jpj
5 px
2jpj21
5 px
p21
:
The next example shows that formula (3.4.1) is also valid for p 5 1/2.
¥
⁄ EXAMPLE 3 For p 5 1/2, formula (3.4.1) can be written as
d
dx
ffiffiffi
x
p
5
1
2
ffiffiffi
x
p
: ð3:4: 2 Þ
Verify that equation (3.4.2) holds for all x . 0.
3.4 Differentiation of Some Basic Functions 201

Solution We verify this formula by referring to the definition of the derivative.
Since
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
ffiffiffi
x
p
Δx
5
ð
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
ffiffiffi
x
p
Þð
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
1
ffiffiffi
x
p
Þ
Δxð
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
1
ffiffiffi
x
p
Þ
5
ð
ffiffiffiffiffiffiffiffiffiffiffiffiffi
x1Δx
p
Þ
2
ð
ffiffiffi
x
p
Þ
2
Δxð
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
1
ffiffiffi
x
p
Þ
5
ðx 1 ΔxÞx
Δxð
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
1
ffiffiffi
x
p
Þ
5
Δx
Δxð
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
1
ffiffiffi
x
p
Þ
5
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
1
ffiffiffi
x
p
;
we conclude that
d
dx
ffiffiffi
x
p
5 lim
Δx-0
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
ffiffiffi
x
p
Δx
5 lim
Δx-0
1
ffiffiffiffiffiffiffiffiffiffiffiffiffiffiffi
x 1 Δx
p
1
ffiffiffi
x
p
5
1
ffiffiffiffiffiffiffiffiffiffiffi
x 1 0
p
1
ffiffiffi
x
p
5
1
2
ffiffiffi
x
p
: ¥
Now that we have verified formula (3.4.1) for one value of p that
is not an
integer, it is reasonab le to wonder if (3.4.1) is valid for other values of p. Indeed, it
is. We record this fact as a theorem for now, but we defer the proof until Section
5.6. In the meantime, you should use this differentiation formula whenever it is
needed.
THEOREM 1
(The Power Rule)Ifp is any real number, then
d
dx
x
p
5 px
p21
:
⁄ EX
AMPLE 4 Differentiate
1
4x
12
1
6x
7=3
2 2
x
2
with respect to x .
Solution After
rewriting the given expression as a sum of three monomials, we use
Theorem 1 with p 5212, p 5 1/3, and p 522:
d
dx
1
4x
12
1
6x
7=3
2 2
x
2
5
d
dx
1
4
x
212
1 6x
1=3
2 2x
22
5
1
4
ð212Þx
213
1 6
1
3
x
22=3
2 2ð22Þx
23
52
3
x
13
1
2
x
2=3
1
4
x
3
: ¥
⁄ EXAMPLE 5 In an adiabatic (no heat in or out) argon system, the third
po
wer of pressure (P) is inversely proportional to the fifth power of volume (V). At a
pressure of 1000 atmospheres (atm), the volume of the argon sample is 34 cm
3
. What
is the rate of change of pressure with respect to volume when the sample is 50 cm
3
?
Solution According
to the given information, there is a proportionality constant k
such that P
3
5 k/V
5
,orP 5 cV
25/3
where c 5 k
1/3
. Our first step is to find the value of
c by substituting P 5 1000 atm and V 5 34 cm
3
into the equation P 5 cV
25/3
.We
obtain
202 Chapter 3 The Derivative
1000 atm 5 c ð34 cm
3
Þ
25=3
;
or c 5 1000 34
5/3
atm 3 cm
5
. Therefore using Theorem 1 with p 525/3, we calculate
d
dV
P 5
d
dV
ðcV
25=3
Þ
52
5c
3
V
28=3
52
5000 34
5=3
3
V
28=3
atm cm
5
and
dP
dV
V550 cm
3
5
5000 34
5=3
3
3 ð50 cm
3
Þ
8=3
atm 3 cm
5
17:5
atm
cm
3
: ¥
Before we turn our attention to other types of functions, we prove one simple
consequenc
e of the Power Rule.
THEOREM 2
The derivative p
0
of a polynomial p is a polynomial. If p is not a
constant, then the degree of p
0
is one less than the degree of p.Ifp is a constant,
then p
0
is identically 0.
Proof. If p(x) 5 a
N
x
N
1 a
N21
x
N21
1 1 a
2
x
2
1 a
1
x 1 a
0
with a
N
6¼0, then, on
applying the Power Rule to each term of p(x), we obtain
p
0
ðxÞ5 N a
N
x
N21
1 ðN 2 1Þa
N21
x
N22
1 1 2 a
2
x 1 a
1
;
from which the asserted results follow. ’
Trigonometric
Functions
We continue to build our library of differentiation formulas by finding the de ri-
vatives of the remaining trigonometric functions. We have already seen how to
differentiate sine and cosine (Section 3.2) and secant (Example 4 of Section 3.3).
The other trigonometric functions can now be handled easily. Before doing so,
recall that we often write sin
2
(x) and tan
2
(x) rather than (sin (x))
2
and (tan (x))
2
.
THEOREM 3
The derivatives of tan (x), cot (x), and csc (x) are
d
dx
tanðxÞ5 sec
2
ðxÞ; ð3:4:3Þ
d
dx
cotðxÞ52csc
2
ðxÞ; ð3:4:4Þ
and
d
dx
cscðxÞ52csc ðxÞcotðxÞ: ð3:4:5Þ
3.4 Differentiation of Some Basic Functions 203
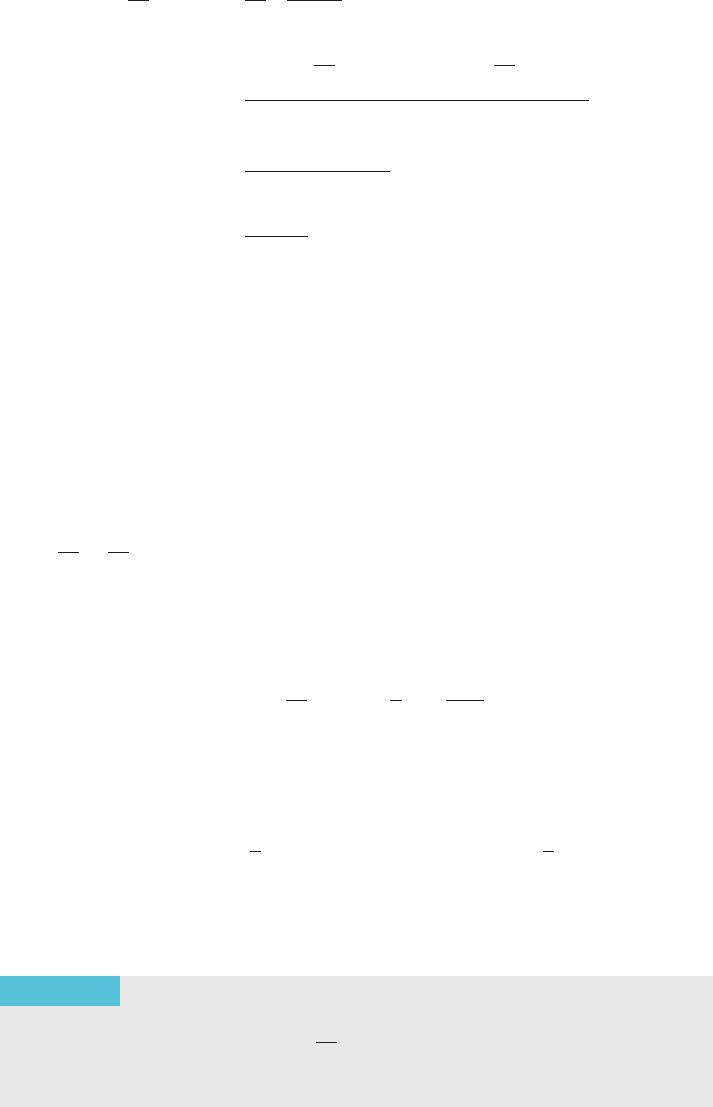
Proof. We use the Quotient Rule to prove formula (3.4.3):
d
dx
tanðxÞ 5
d
dx
sinðxÞ
cosðxÞ
5
cosðxÞ
d
dx
ðsinðxÞÞ2 sinðxÞ
d
dx
ðcosðxÞÞ
cos
2
ðxÞ
5
cos
2
ðxÞ1 sin
2
ðxÞ
cos
2
ðxÞ
5
1
cos
2
ðxÞ
5 sec
2
ðxÞ:
The proof of formula (3.4.4) is similar and is left as Exercise 66. The proof of
equation (3.4.5) is analogous to the derivation of formula (3.3.1) and is left as
Exercise 67. ’
⁄ EX
AMPLE 6 Find the tangent line to the graph of y 5 x cot
(x) at the point
ðπ=6; π
ffiffiffi
3
p
=6Þ:
Solution We
first find the slope. Using the Product Rule, we calculate:
dy
dx
5
d
dx
xcotðxÞ
5 1 cotðx Þ1 x
csc
2
ðxÞ
5 cotðxÞx csc
2
ðxÞ:
Evaluating at x 5 π/6, we find the slope to be
ffiffiffi
3
p
2 ðπ=6Þ2
2
5
ffiffiffi
3
p
2 2π=3:
According to formula (3.1.12), the point-sl ope equation of the tangent line is
y 5
ffiffiffi
3
p
2
2π
3
x 2
π
6
1
π
ffiffiffi
3
p
6
: ¥
The Derivative of the
Natural Exponential
Function
In Section 2.6, we introduced the number e, and, in Example 8 from that section,
derived the basic formulas
e
x
5 lim
n-N
11
x
n
n
and e
x
5 lim
n-N
12
x
n
2n
: ð3:4:6Þ
We will now see that the exponential function x/e
x
, or exp(x), has the remarkable
property that it is its own derivative.
THEOREM 4
For every x, we have
d
dx
e
x
5 e
x
ð3:4:7Þ
or, equivalently,
204 Chapter 3 The Derivative
