Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

expðxÞ5 expðxÞ: ð3:4:8Þ

Proof. Let f (x) 5 e

. We will ﬁrst show that (3.4.7) holds for x 5 0. Because

f(0) 5 e

5 1 and

ð0Þ5 lim

h-0

2 e

5 lim

h-0

2 1

;

we must show that

lim

h-0

2 1

5 1: ð3:4:9Þ

As a ﬁrst step, we will prove the one-sided limit

lim

h-0

2 1

5 1: ð3:4:10Þ

The numerical evidence supporting this equation is certainly compelling:

h 10

1.00050017 1.00005000 1.00000500 1.000000 50 1.00000005 1.000000 00

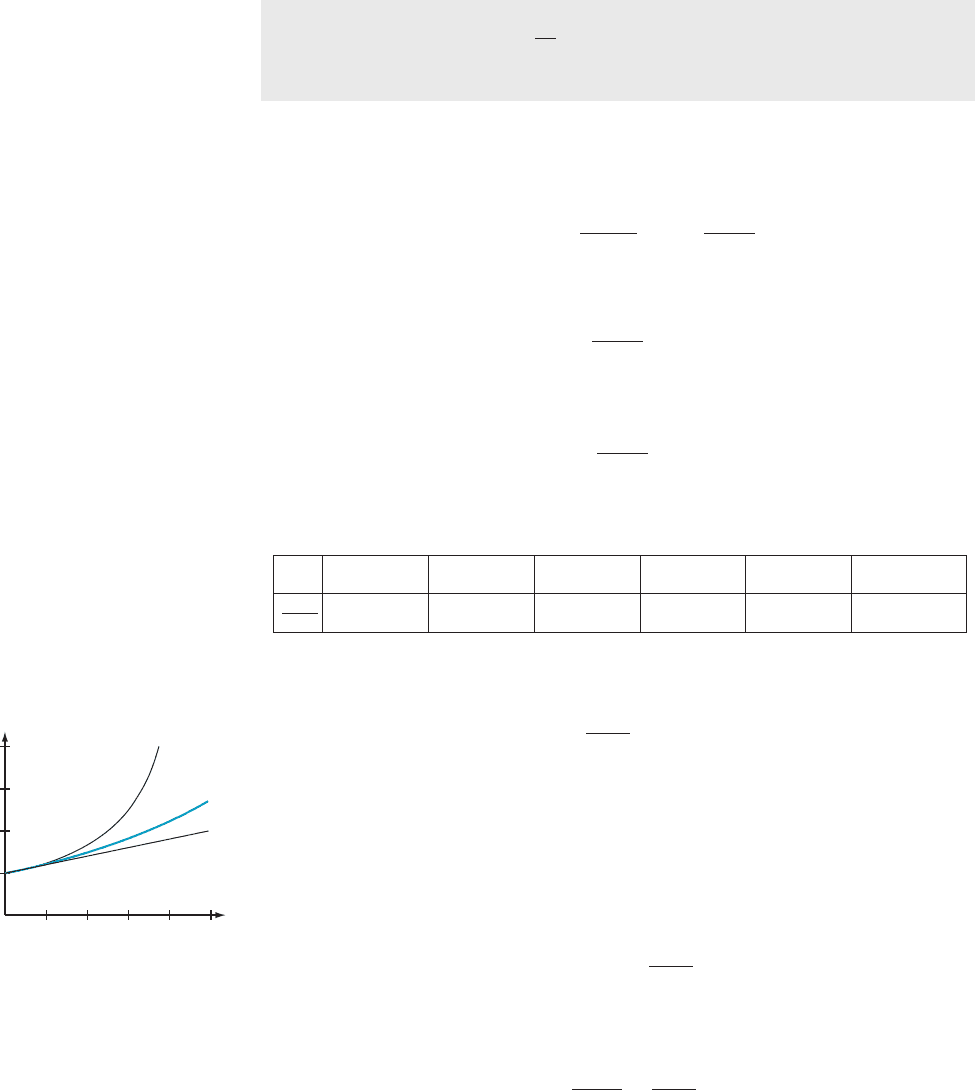
So is the graphical evidence. In Figure 1, we see that

1 1 h , e

1 2 h

ð0 , h , 1Þð3:4:11Þ

In fact, we know that (11h/x)

increases to e

as x tends to inﬁnity—refer to the

Insight following Example 8 of Section 2.6. Taking x 5 1, we see that 1 1 h , e

which is the ﬁrst inequality of line (3.4.11). From Section 2.6 we also know that

(1 2 h/x)

decreases to e

as x tends to inﬁnity. Taking x 5 1, we see that

, (1 2 h)

, which is the second inequality of line (3.4.11). Subtracting 1 from

each part of line (3.4.11) and simplifying 1/(1 2 h) 2 1toh/(1 2 h), we have

h , e

2 1 ,

1 2 h

Dividing by h (which is positive), we obtain

1 ,

2 1

1 2 h

Because lim

h-0

ð1=ð1 2 hÞÞ5 1, the Pinching Theorem of Section 2.2 establishes

limit formula (3.4.10).

0.2 0.4 0.6 0.8 1

y  1/(1  h)

y  e

y  1  h

m Figure 1

3.4 Differentiation of Some Basic Functions 205

Next, we complete the proof of two-sided limit (3.4.9). We note that if u 52h,

then u - 0

as h - 0

. It follows that

lim

u-0

2 1

5 lim

u-0

1 2 e

2 u

5 lim

u-0



2 1

2 u



5 lim

u-0

lim

u-0

2 1

2 u

5 1  lim

h-0

2 1

ð3:4:10Þ

Together, this limit formula and (3.4.10) imply the two-sided limit (3.4.9).

Finally, we obtain (3.4.7) for a general value of x by reducing to the x 5 0 case

as follows:

ðxÞ 5 lim

h-0

f ðx 1 hÞ2 f ðxÞ

5 lim

h-0

x1h

2 e

5 lim

h-0

2 e

5 e

lim

h-0

2 1

5 e

by (3.4.9). ’

⁄ EXAMPLE 7 Suppose that an object vibrates about its equilibrium posi-

tion

according to the formula x(t) 5 e

sin (t) mm . (Resistance to movement gives

rise to the “damping” factor e

.) At what speed is the object moving when t 5 1?

Solution We

compute x

(t) by means of the Quotient Rule:

ðtÞ 5



sinðtÞ



sinðtÞ2 sinðtÞ

ðe

cosðtÞ2 e

sinðtÞ

cosðtÞ2 sinðtÞ

Therefore

ð1Þ5

cosð1Þ2 sinð1Þ

 2 0:1108: ¥

206 Chapter 3 The Derivative

Summary of Derivatives of Basic Functions

ðx

Þ 5 px

p21

2 N , p , N

sinðxÞ 5 cosðxÞ

cosðxÞ 52sinðxÞ

tanðxÞ 5 sec

ðxÞ

cotðxÞ 52csc

ðxÞ

secðxÞ 5 secðxÞtanðx Þ

cscðxÞ 52cscðxÞcotðxÞ

5 e

QUICK QUIZ

1. Differentiate x

3/2

with respect to x .

2. Differentiate csc (x) cot (x) with respect to x.

3. What is lim

x-0

ðe

2 1Þ=x?

4. Differentiate xe

with respect to x.

Answers

1. (3/2) x

1/2

2. 2csc (x) cot

(x) 2 csc

(x) 3. 1 4. (x 1 1)e

EXERCISES

Problems for Practice

c In Exercises 128 differentiate the given expression with

respect to x. b

1. 8x

2 6x

2. 2x

3/2

2 1/x

3/2

3. 6x

5/3

2 25x

3/5

ﬃﬃﬃﬃﬃ

1 3=

ﬃﬃﬃ

5. 2x1e

6. xe

7. e

3/2

ﬃﬃﬃ

cscðxÞ

9. x

cot (x)

10. x/tan (x)

11. secðxÞ=

ﬃﬃﬃ

12. sec (x) 2 tan (x)

13. csc (x) 1 cot (x)

14. x cot (x) 2 csc (x)

15. csc (x) cot (x)

16. x

tan (x)

17. tan (x) sec ( x)

18. x

19. e

sin (x)

20. 2/(cot (x) 2 csc (x))

21. 3/(5 1 7e

)

22. x/(2 1 tan (x))

23. (1 1 sec (x))/tan (x)

24. ð1 2

ﬃﬃﬃ

Þ=ð1 1

ﬃﬃﬃ

25. x

/(x 1 e

)

26. e

cos (x)

27. x

1/3

/(1 1 x

2/3

)

28. (e

2 1)/(e

1 1)

3.4 Differentiation of Some Basic Functions 207

c In Exercises 2936, ﬁnd the tangent line to the graph of

y 5 f(x)atP. b

29. f (x) 5 3x

2/3

, P 5 (8, 12)

30. f ðxÞ5 6=ð1 1

ﬃﬃﬃ

Þ; P 5 ð4; 2Þ

31. f (x) 5 x

sin (x), P 5 (π,0)

32. f (x) 5 x

1 tan (x), P 5 (0, 0)

33. f (x) 5 tan (x) sec (x), P 5 (π/3, 2

ﬃﬃﬃ

)

34. f (x) 5 e

, P 5 (0, 1)

35. f (x) 5 8x tan (x), P 5 (π/4, 2π)

36. f (x) 5 csc (x)/x, P 5 (π/6, 12/π)

c In each of Exercises 3740, use the Product Rule to dif-

ferentiate

the given expression with respect to x. b

37. e

38. tan

(x)

39. csc

(x)

40. tan (x) 1 tan

(x)

Further Theory and Practice

c In Exercises 4144, ﬁnd a polynomial whose derivative is

the given polynomial. b

41. 7x

2 4x 1 6

42. x

2 2x

2 1

43. x

1 6x

2 3x

44. 10x

1 x

1 4x 2 3

c In Exercises 4548, ﬁnd a function whose derivative is the

given

function. b

45. 1=

ﬃﬃ

ﬃ

46. 3/x

47. 28 csc

(x)

48. cos (x) (5 csc

(x) 2 1)

49. Suppose that p is a polynomial. We say that α is a root of

p of multiplicity m if there is a polynomial q with q(α) 6¼0

and p(x) 5 (x2α)

q(x). Prove that if α is a root of p of

multiplicity m, then α is a root of p

of multiplicity m 2 1.

50. What is the equation of the line that is tangent to the

graph of y 5 e

at the point (t, e

)? What are the x- and y-

intercepts of this line?

51. Find a function whose derivative is tan

(x).

52. Let p be a ﬁxed number. Let C be any number. Show that

y(x) 5 Cx

is a solution of the differential equation

5 py:

c In Exercises 5356, compute f

53. f (x) 5 x

(2x 1 1), c 521

54. f (x) 5 x

(2x 2 1)

, c 5 2

55. f (x) 5 (x

1 2x

2 3)(2x

1 7x 2 2), c 5 1

56. f (x) 5 (x

1x 2 1)(2x

2 3)

, c521

57. Let f (x) 5 sec

(x) 2 tan

(x). Use the Product Rule to

differentiate each summand of f. Simplify to show that

(x) 5 0 for each x in the domain of f. How can you

obtain this result more easily?

58. Let f

(x) 5 x

for every positive integer n. Find f

terms of f

and f

n21

59. Relate the limit

lim

h-0

h=2

2 e

2h=2

to a derivative and evaluate it.

60. Let f (x) 5 tan (x). For every t 2(2π/2,π/2), write down

the equation of the tangent line to the graph of f at

(t, f (t)) in the form

x 5 MðtÞðy 2 tanðtÞÞ1 t :

What function is M(t)? What line results when you

compute

x 5 lim

t-ðπ=2Þ

ðMðtÞðy 2 tanðtÞÞ1 tÞ?

Is it an asymptote of f ?

61. Show that

jxj

5 p

jxj

ðx 6¼ 0Þ:

62. Suppose that p is a degree n polynomial, and q is a degree

m polynomial. What is the degree of (p q)

?Of(p 3 q)

Of the numerator and denominator of (p/q)

(before

performing any cancellations)?

63. Find all values of c such that the intercepts of the tangent

line to y 5 e

at (c, e

) are equidistant from the origin.

64. Let g(x) 5 e

where k is a constant. Using the deﬁnition

of the derivative, show that

ðxÞ5 g

ð0ÞgðxÞ:

65. Suppose that 0 , p , 2. For x . 0, let

f ðxÞ5

1 1

Find the point at which the graph of f has a horizontal

tangent line.

66. Write cot (x) 5 cos (x) / sin (x), and use the Quotient

Rule, as in the derivation of equation (3.4.3), to verify the

formula

cotðxÞ52csc

ðxÞ:

67. Write sec (x) 5 1/cos (x), and use the Reciprocal Rule to

verify the formula

cscðxÞ52cscðxÞcot ðxÞ:

If x and f (x) measure physical quantities that bear units

(such as meters, grams, seconds, etc.), then the difference

quotients that are used in deﬁnition (3.2.1) also bear

208 Chapter 3 The Derivative

units, which are imparted to f

(x). Exercises 6870 per-

tain to dimensional analysis, which requires that the

dimensions of both sides of an equation are the same.

68. Suppose that y 5 x

. Use dimensional analysis to predict

the correct value of α in the equation dy/dx 5 px

69. In the Product Rule for ( f g)

(t), there is a term f

(t) 

g(t) and a term f (t) g

(t) but no term involving f

(t) g

(t).

Use dimensional analysis to explain why no such term

should be present.

70. Show that the Quotient Rule for ( f / g)

(t) is dimension-

ally correct. That is, the Quotient Rule leads to the cor-

rect units for the derivative of a quotient.

71. If q( p) is the demand for a product at price p—that is, the

number of units of the product that are sold at price p—

then E( p) 52q

( p)  p/q( p) is called the elasticity of

demand for the product at price p. Suppose that a and b

are positive constants.

a. What is E( p)ifq( p) 5 a2bp?

b. What is E( p)ifq( p) 5 a/p

72. The hyperbolic sine and hyperbolic cosine functions are

deﬁned by

coshðxÞ5

1 e

and

sinhðxÞ5

2 e

Express cosh

(x) in terms of sinh (x) and sinh

(x)in

terms of cosh (x).

73. The hyperbolic tangent (tanh) and hyperbolic secant

(sech) are deﬁned by

tanhðxÞ5

sinhðxÞ

coshðxÞ

2 e

1 e

and

sechðxÞ5

coshðxÞ

1 e

Express tanh

(x) and sech

(x) in terms of tanh (x) and

sech (x).

Calculator/Computer Exercises

74. Verify



x50

521

numerically by computing central difference quotients.

c For each of the given functions in Exercises 7578,

graph

f and f

in the given viewing rectangle R. Fill in the following

table. b

Interval

where f

increases

Interval

where f

decreases

Point

at which f has

a horizontal tangent

Interval

where f

. 0

Interval

where f

, 0

Point(s) at

which f

5 0

Use the table to draw inferences that relate the sign of f

the behavior of f. (These relationships will be studied in

Chapter 4.)

75. f (x) 5 2x 1 6 2 5/(x

1 1), R 5 [ 21.3, 0.5] 3 [23.5, 4.2]

76. f (x) 5 11(x

2 1) /(x

1 1), R 5 [23, 1.6] 3 [20.6, 1.9]

77. f (x) 5 x

4/3

/(2 1 sin (x)), R 5 [0, 7] 3 [22.5, 8.25]0

78. f (x) 5 x

sin (x)/(1 1 x 1 x

), R 5 [23, 1.2] 3 [20.9, 2.1]

79. Let g

(x) 5 e

. Plot

k/D

ð0; 10

for 22 # k # 2. Use your plot to determine g

(0).

80. For what values of x . 1, if any, does x/ e

grow faster

than x / x

? When, if ever, does e

catch up in size to

81. Let p

, τ

, μ, and Δ be ﬁxed constants. The set H of

points ( p, τ) in the ﬁrst quadrant of the pτ-plane that

satisfy

ðτ 2 μ

Þp 2 ðτ

2 μ

τÞp

1 2μ

Δ 5 0

is called the Hugoniot curve. It arises in the study of gas

dynamics produced by combustion.

a. Find dτ/dp.

b. Let Q 5 ( p

, τ

) be a point on the Hugoniot curve H.

What is the equation of the line that is tangent to H at Q?

c. Assume that Δ , 0. (This is the mathematical condi-

tion for an exothermic reaction.) Show that the point

( p

,τ

) lies below the Hugoniot curve.

d. Continue to suppose that Δ , 0. Solve for those points

Q on the Hugoniot curve H such that the line tangent

to H at Q passes through the point P 5 ( p

, τ

). The

points that you ﬁnd are known as the Chapman-Jou-

guet points. The tangent lines that you ﬁnd are known

as the Rayleigh lines.

e. Illustrate the Hugoniot curve and its Rayleigh lines for

the speciﬁcations p

5 2.1, τ

5 1.7, μ 5 1/2, and

Δ 522. Label the Chapman-Jouguet points.

82. Graph f (x) 5 (x 1 1)

4/3

(x 2 1)

2/3

for 21.5 # x # 1.5. Does

the graph of f have a tangent line at the point (21, 0)?

At the point (1, 0)? Use the Power Rule to explain the

behavior of the graph of f at these two points.

3.4 Differentiation of Some Basic Functions 209

3.5 The Chain Rule

In principle, we know how to differentiate H(x ) 5 (x

1 x)

100

. All we have to do is

expand the expression and then differentiate. But this would be a great deal of

work, and it turns out that we can avoid it.

Instead, we think of H as the composition of two functions: H 5 g 3 f where

g(u) 5 u

100

and f (x) 5 x

1x. (Recall, that in Section 1.5, we learned how to

recognize compositions of functions.) We know how to differentiate both f and g.

Let’s see how we can use this information to differentiate their composition H.

A Rule for

Differentiating the

Composition of Two

Functions

Imagine car A driving down the road with position given by a(t). Imagine a second

car B driving down the road with position given by b(t). At a given instant, if B is

traveling at a rate of 8 mi/hr (db/dt 5 8), and if A is traveling twice as fast as B, then

it is clear that A is traveling at the rate of 16 mi/hr. In other words, if we know the

rate of change of a with respect to b (in this case, 2) and we know the rate of change

of b with respect to t (in this case, 8), then we know the rate of change of a with

respect to t (namely, 2 8 5 16). Notice that the third quantity is the product of the

ﬁrst two. Schematically we have

rate of change of

with respect to

rate of change of

with respect to

rate of change of

with respect to



This example suggests that

The derivative of a composition is the product of the derivatives of the component functions.

This formula is known as the Chain Rule. It gives us a way to differentiate the

composition of two differentiable functions. The formulation of the Chain Rule in

Leibniz notation is particularly suggestive. It looks as though we are canceling

fractions. As a matter of fact we are not. Derivatives expressed in Leibniz notation

are not fractions. However the “difference quotients” which converge to the

derivative are fractions, and we can cancel those. That observation, if executed with

some care, can be used to prove the Chain Rule. A somewhat different proof may

be found in the Genesis and Development for this chapter.

THEOREM 1

Chain Rule Suppose that the range of the function f is contained

in the domain of the function g.Iff is differentiable at c and if g is differentiable

at f (c), then g 3 f is differentiable at c. Moreover

210 Chapter 3 The Derivative

ðg 3 f Þ



x5c





u5f ðcÞ









x5c



: ð3:5:1Þ

Recall from Section 3.2 that the vertical bar notation indicates the point at

which the derivative is evalua ted. It is important to notice that the two derivatives

on the right side of (3.5.1) are evaluated at different points. When we calculate

(g 3 f)(x) 5 g( f (x)), we evaluate g at f (x), and we evaluate f at x. Thi s evaluation

scheme is preser ved in the application of the Chain Rule: In computing the de ri-

vative of g 3 f at c, the derivative of g is evaluated at f (c) and the derivative of f is

evaluated at c. Thus while the basic idea of the Chain Rule is that the derivative of

a composition is the product of the derivatives, the statement of the Chain Rule is a

bit complicated because we have to be careful about where we evaluate the

derivatives!

With primes denoting derivatives, the Chain Rule becomes

ðg 3 f Þ

ðcÞ5 g

ðf ðcÞÞ  f

ðcÞ:

INSIGHT

It is sometimes useful to think of a composition as having an “outside

function” and an “inside function.” The outside function is the last function applied: In

the composition g 3 f, it would be g. In applying the Chain Rule to such a composition, we

differentiate the outside function ﬁrst, holding the inside function ﬁxed. Then we dif-

ferentiate the inside function (which would be f in the composition g 3 f ). Keep this point

of view in mind when reading the examples that follow.

Some Examples ⁄ EXAMPLE 1 Differentiate H(x) 5 sin (3x

1 1).

Solution We

write H 5 g 3 f wher e g(u) 5 sin (u) is the “outside function” and

f (x) 5 3x

1 1 is the “inside function.” Then

5 cosðuÞ and

5 6x:

As a result,



u5f ðxÞ



5 cosðf ðxÞÞ  ð6xÞ

5 ðcosð3x

1 1ÞÞ  6x:

Using the idea in the preceding Insight, we have the following solution scheme:

3.5 The Chain Rule 211

ðxÞ

|ﬄﬄ{zﬄﬄ}

5 cos

|{z}



1 1

|ﬄﬄﬄﬄ{zﬄﬄﬄﬄ}



 6x

|{z}

derivative

composed

function

derivative

outside

function

inside

function

derivative

inside

function ¥

⁄ EX

AMPLE 2 Differentiate H(x) 5 (x

1 x)

100

Solution We

write H 5 g 3 f where g(u) 5 u

100

and f (x) 5 x

1 x. According to the

Chain Rule,





u5f ðxÞ











Now

5 100u

and

5 3x

1 1:

Therefore

5 ð100  u



u5f ðxÞ

ð3x

1 1Þ



100  f ðxÞ



ð3x

1 1Þ



100ðx

1 xÞ



ð3x

1 1Þ ¥

INSIGHT

The merit of using functional notation when applying the Chain Rule is

that evaluation issues can be incorporated directly into the notation. There is an alter-

native notation that employs variables rather than explicit functions. It is encountered

frequently because it is more streamlined and easier to remember. The idea is that if y

depends on u, and u depends on x, then y depends on x. The Chain Rule expresses the

relationship between the derivatives of these variables as follows:

: ð3:5:2Þ

In using formula (3.5.2), it must be understood that the variable y on the left side is a

function of x. Its rate of change must therefore be expressed in terms of x alone. Any u

that remains on the right side of (3.5.2) must be written in terms of x in order to complete

the calculation. Thus in Example 2, we set y 5 u

100

, u 5 x

1 x, and, after applying (3.5.2),

we replace u with x

1 x:



100



ðx

1 xÞ



5 100u

ð3x

1 1Þ5 100ðx

1 xÞ

ð3x

1 1Þ:

212 Chapter 3 The Derivative

⁄ EXAMPLE 3 Find the tangent line to the graph of H(x) 5 tan

(x) at the

point (π/4, 1).

Solution Writi

ng tan

(x) as (tan (x))

makes it clearer that u/ u

is the “outside”

function. Thus H 5 g 3 f where g(u) 5 u

,andf (x) 5 tan (x). Now g

(u) 5 7u

, and

(x) 5 sec

(x). Notice that g

( f (x )) 5 7f ( x )

5 7f

(x). We can now compute

(x) 5 (g 3 f)

(x):

ðxÞ 5 g

ðf ðxÞÞ  f

ðxÞ

5 7  f

ðxÞsec

ðxÞ

5 7  tan

ðxÞsec

ðxÞ:

It follows that the slope of the tangent line to the graph of H at (π/4, 1) is





5 7tan





sec





5 7  1

ð

ﬃﬃﬃ

5 14:

Thus the tangent line’s equation in point-slope form is y 5 14 (x2π/4) 1 1.

INSIGHT

Make sure that you understand the difference between g

( f (x)) and

(g 3 f )

(x). Because f plays a role in the formation of the function g 3 f , its rate of

change f

(x) is a component of the rate of change (g 3 f )

(x). On the other hand,

( f (x)) means the rate of change of g at the point f (x) : the rate of change of f plays

no role in this last quantity.

Examples 2 and 3 involve an application of the Chain Rule that arises fre-

quently. In each example, we considered a function f that has be en raised to a ﬁx ed

power p. Because this type of composition occurs so often, it is worthwhile stating

this special case of the Chain Rule:

The Chain Rule—Power Rule

f ðxÞ

5 pfðxÞ

p21

f ðxÞð3:5:3Þ

Alternatively, if we write u 5 f (x), then formula (3.5.3) becomes

5 pu

p21

: ð3:5 :4Þ

⁄ EX

AMPLE 4 Use formula (3.5.3) to derive the Reciprocal Rule of

Section 3.3.

Solution If

we take p 521 in the Chain RulePower Rule, then we have



f ðxÞ



ðf ðxÞÞ

5 ð21Þ f ðxÞ

f ðxÞ52

ðxÞ

f ðxÞ

;

as required.

3.5 The Chain Rule 213

Multiple Compositions Of course, some functions are the composition of more than two simpler functions.

To differentiate such a function, we must apply the Chain Rule several times.

⁄ EX

AMPLE 5 Differentiate Q(x) 5 sin

(5x).

Solution We

can write Q as Q 5 H 3 (G 3 F ) where H(s) 5 s

, G(u) 5 sin (u), and

F (x) 5 5x. With this grouping, Q is the composition of two functions, H and G 3 F.

By the Chain Rule,





s5G 3 FðxÞ







dðG 3 FÞ



: ð3:5:5Þ

Now we apply the Chain Rule a second time to the composition G 3 F to obtain

dðG 3 FÞ





u5FðxÞ









Substituting this last equation into equation (3.5.5) now yields





s5G 3 FðxÞ









u5FðxÞ









Finally, we calculate that

ðsÞ5 3s

;

ðuÞ5 cos ðuÞ; and

ðxÞ5 5:

Therefore

5 3



GðFðxÞÞ



 cos



FðxÞ



 5

5 15 sin

ð5xÞcosð5xÞ: ¥

INSIGHT

It is worth noticing that the philosophy of differentiating the outside

function ﬁrst and working toward the inside applies even in the case of multiple

compositions. You should review Example 5 with this observation in mind.

An Application The Chain Rule allows us to investigate new kinds of rate-of-change problems. We

conclude with an example.

⁄ EX

AMPLE 6 An oil slick spreads so that it forms a disk centered around

the point of contamination. As the ﬁxed volume of spilled oil disper ses, and the

thickness of the slick decreases, the radius of the slick increases at the rate of 2 ft

per minute. How fast is the area of polluted surface water growing when the radius

is 500 ft?

Solution The

area of polluted surface water is given by A 5 πr

. The radius r of the

slick is a function of time t (with dr/dt 5 2 ft/min)}. It follows that A depends on t as

well. We use Leibniz notation and differentiate both sides of the equation A 5 πr

with respect to t to obtain



ðπr

Þ

5 ðπ  2rÞ

214 Chapter 3 The Derivative