Blank B.E., Krantz S.G. Calculus: Single Variable

Подождите немного. Документ загружается.

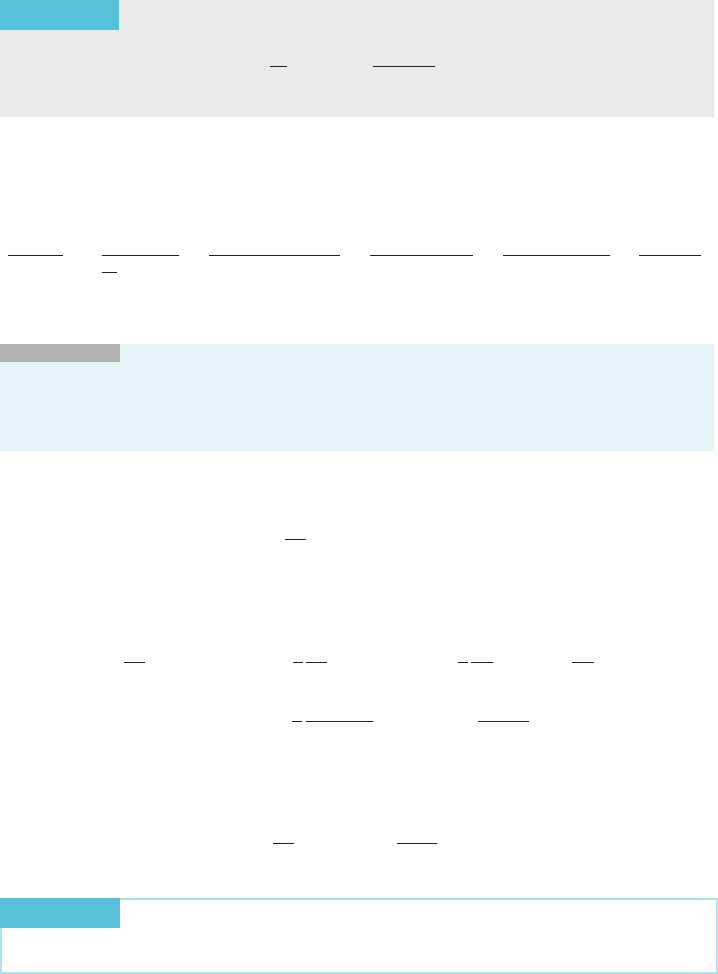
THEOREM 4

Let a be a positive constant not equal to 1. For every t . 0, we have

log

ðtÞ5

t  lnðaÞ

: ð3:6:8Þ

Proof. Let f (s) 5 a

. Then f

(t) 5 log

(t). Using equation (3.5.6) for f

(s)and

applying the Inverse Function Derivative Rule, we have

dðf



s5f

ðtÞ

 lnðaÞj

s5f

ðtÞ

 lnðaÞ

log

ðtÞ

 lnðaÞ

t  lnð a Þ

’

INSIGHT

Notice that Theorem 4 generalizes formula (3.6.7) for the derivative of the

natural logarithm function: when a is taken to be e, the factor ln(a) becomes ln (e), which

is 1, and formula (3.6.8) reduces to (3.6.7). This gain in simplicity is one reason that e is

the preferred base for the logarithm function in calculus.

⁄ EXAMPLE 6 Calculate

log

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 2

Þ:

Solution Before

differentiating, we use Theorem 2(e) of Section 2.6 to simplify

the logarithm. Then we set u 5 1 1 2

and use formula (3.6.8) together with the

Chain Rule:

log

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 2

Þ5

log

ð1 1 2

Þ5

log

ðuÞ

u  lnð2Þ

 2

lnð2Þ5

x21

1 1 2

: ¥

Logarithmic

Differentiation

We next show how to use the logarithm as an aid to differentiation. The key idea is

that if f is a function taking positive values, then we can exploit the formula

lnðf ðxÞÞ5

ðxÞ

f ðxÞ

: ð3:6:9Þ

DEFINITION

The derivative of the logarithm of f is called the logarithmic deriva-

tive of f. The process of differentiating ln( f (x)) is called logarithmic differentiation.

As the right side of equation (3.6.9) indicates, the logarithmic derivative of

f measures the relative rate of change of f. This quantity often conveys more useful

information than f

itself. It is used frequently in biology, pharmacology, medicine,

and economics. For example, consider an item whose price is increasing at the rate

of $100 per month. Is that a signiﬁcant rate of change? The answer depends on the

price of the item. For a $150,000 house, the relative rate of change is only 1/1500

per month, or 0.80% per year. If the item is a $1500 computer system, then the

relative rate of change is 1/15 per month, or 80% per year.

3.6 Derivatives of Inverse Functions 225

Logarithmic differentiation is also useful in calculus, where we use the alge-

braic properties of the logarithm to simplify complicated products and quotients

before differentiating. Logarithmic differentiation can also be an effective techni-

que for ﬁnding the derivative of an expression that involves an exponent that is a

function. The next two examples will illustrate these ideas.

⁄ EX

AMPLE 7 Calculate the derivative of the function f (x) 5 x

Solution First

we take the natural logarithm of both sides:

ln ðf ðxÞÞ 5 lnðx

5 x  lnðxÞ:

Then we differentiate each side, using the Product Rule to calculate the derivative

on the right side:

lnðf ðxÞÞ5 1  lnðxÞ1 x 

5 lnðxÞ1 1:

Next we use form ula (3.6.9) to simplify the left side:

ðxÞ

f ðxÞ

5 lnðxÞ1 1:

Finally we solve for f

(x):

ðxÞ5 f ðx ÞðlnðxÞ1 1Þ5 x

ðlnðxÞ1 1Þ: ¥

INSIGHT

Notice that we cannot solve Example 7 by using the Power Rule

(Theorem 1 from Section 3.4):

6¼ x  x

x21

5 x

This incorrect computation treats the exponent x as if it were constant. The Power Rule

can be used only when the exponent is constant. Nor can we use formula (3.5.6) with a 5 x:

6¼ ln ðxÞx

This incorrect computation treats the base x as if it were constant. Formula (3.5.6) can be

used only when the base is constant.

The difﬁculty of Example 7 is that both the base and the exponent involve the variable

of differentiation. Applying the logarithm succeeds by removing the variable from the

exponent position. Another approach is to use formula (3.5.7) with a 5 x to remove the

variable from the base position. We obtain

5 e

x lnðxÞ

;

from which we obtain the result of Example 7 as follows:

x lnðxÞ

5 e

x lnðxÞ

ðx lnðxÞÞ5 e

x lnðxÞ

ðlnðxÞ1 1Þ5 x

ðlnðxÞ1 1Þ:

⁄ EXAMPLE 8 Calculate the derivative of

f ðxÞ5

 e

1 1 x

226 Chapter 3 The Derivative

Solution This calculation can be done in a straightforward but tedious fashion

by means of the Quotient Rule and the Product Rule. Use of Logarithmic

Differentiation reduces the algebra that is necessary. To start, we apply the

natural logarithm to each side:

lnðf ðxÞÞ5 lnðx

Þ1 lnðe

Þ2 lnð1 1 x

Þ5 3lnðxÞ1 x 2 lnð1 1 x

Þ:

Next, we differentiate each side of the last equ ation with respect to x. We obtain

ðxÞ

f ðxÞ

1 1 2

1 1 x

Finally,

ðxÞ 5 f ðxÞ



1 1 2

1 1 x



 e

1 1 x





1 1 2

1 1 x



Summary of Derivatives of Basic Functions

ðx

Þ 5 px

p21

2N , p , N

sinðxÞ 5 cosðxÞ

cosðxÞ 52sinðx Þ

tanðxÞ 5 sec

ðxÞ

cotðxÞ 52csc

ðxÞ

secðxÞ 5 secðxÞtan ðxÞ

cscðxÞ 52csc ðxÞcotðxÞ

5 e

5 a

 lnðaÞ

lnðxÞ 5

log

ðxÞ 5

x  lnðaÞ

3.6 Derivatives of Inverse Functions 227

QUICK QUIZ

1. If f (x) 5 x 1 exp (x), then what is ( f

)

(1)?

2. Calcul ate f

(x) for f (x) 5 lnðxÞ1 1=x:

3. Calcul ate f

(x) for f (x) 5 log

ðx

Þ:

4. Express π

as a power of e.

Answers

1. 1/2 2. (x 2 1)/x

3. 2/(x ln(3)) 4. e

7 ln(π)

EXERCISES

Problems for Practice

c In Exercises 18, assume that f : R - R is invertible and

differentiable. Compute ( f

)

(4) from the given information. b

1. f

(4) 5 1, f

(1) 5 2

2. f

(4) 5 3, f

(3) 5 1/6

3. f

(4) 521, f

(21) 5 3

4. f

(4) 5 7, f

(7)523/8

5. f

(4) 5 1, f

(s) 5 5s

1 1

6. f

(4) 5 1, f

(s) 5 4 1 πcos (πs)

7. fð

ﬃﬃﬃ

Þ5 4, f

(s) 5 (2 1 s

)/(1 1 s

)

8. f (0) 5 4, f

(s) 5 2e

1 e

c In Exercises 9 26, use the Inverse Function Derivative

Rule to calculate ( f

)

(t). b

9. f :(2N, N) - (2N, N), f (s) 5 3s 2 5

10. f :

(0,N) - (0, N), f (s) 5

ﬃﬃ

11. f : (1,N) - (0, 1/2), f ( s ) 5 1=

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

s 1 3

12. f : (0,N) - (4, N), f (s) 5 s

1 4

13. f : (0, 3) - (2, 245), f (s) 5 s

1 2

14. f :(2N,N) - (0, N), f (s) 5 exp (1 2 s)

15. f : (1, 3)- (3, 15), f (s) 5 s

1 2s

16. f : (1, 8)- (1/64, 1), f (s) 5 1/s

17. f : (0, 4)- (3, 5), f (s) 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 9

18. f : (1/2, 5)- (21/3, 2/3), f (s) 5 (s 2 1) /(s 1 1)

19. f : (1, 2)- (2, 5/2), f (s) 5 (s

1 1)/s

20. f : (1,N)- (2N, N), f (s) 5 ln (s

2 1)

21. f : (0, 1)- (1, e), f (s) 5 exp ð

ﬃﬃ

22. f : (0,N)- (1, N), f (s) 5 exp (s

)

23. f : (0,N)- (0, N), f (s) 5 log

(1 1 s)

24. f : (1,N)- (2, N), f (s) 5 log

(6 1 3

)

25. f :(2N,N)- (0, N), f (s) 5 2

26. f :(2π/2, π/2)- (2N, N), f (s) 5 tan (s)

c In each of Exercises 2749, differentiate the given

expression

with respect to x. b

27. ln

(2x)

28. ln (x

1e)

29. x ln (x) 2x

30. ln (1 1 exp (x))

31. ln (x)/x

32. x/ln (x)

33. 6

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

lnðxÞ

34. ln

(x)

35. ln (sec (x))

36. cos (ln (x))

37. ln (ln (x))

38. ln



x 2 1

x 1 1



39. ln (x 1 exp (x))

40. 2

ln(x)

41. 3

log

ðxÞ

42. log

(5x)

43. log

(5x 1 3)

44. 1/(5 1 log

(x))

45. 2

log

(1 1 4x)

46. x log

(x)

47. x

log

(62x)

48. log

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 1 9

49. log

(log

(x))

c In each of Exercises 5055, a function f is

given. Use

logarithmic differentiation to calculate f

(x). b

50. f (x) 5 (2x 1 1)

1 2)

1 2x 1 1)

51. f (x) 5 ( x

1x)

2 1)

/(x

1 2)

52. f (x) 5 ( x

1 1)

sin

(x) cos

(x)

53. f (x) 5 x

54. f (x) 5 x

sin (x)

55. f (x) 5 x

ðx

Further Theory and Practice

c In Exercises 5659, evaluate the derivative f

of the given

function f in two ways. First, apply the Chain Rule to f (x),

without simplifying f (x) in advance. Second, simplify f (x),

and then differentiate the simpliﬁed expression. Verify that

the two expressions are equal. b

56. f (x) 5 ln

(3x)

57. f (x) 5 ln (x

)

228 Chapter 3 The Derivative

58. f (x) 5 ln (xe

)

59. f (x) 5 ln ð1=

ﬃﬃﬃ

c In each of Exercises 6063, the given function f is

inver-

tible on an open interval containing the given point c. Write

the equation of the tangent line to the graph of f

at the

point ( f(c), c). b

60. f (s) 5

ﬃﬃ

, c 5 9

61. f (s) 5 1/

ﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

s 1 3

, c 5 6

62. f (s) 5

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

1 9

, c 5 4

63. f (s) 5 s

1 2, c 5 1

c In Exercises 6471, ﬁnd f

(γ) for the given f and γ (but

do not try to calculate f

(t) for a general value of t). Then

calculate ( f

)

(γ). b

64. f (s) 5 s

1 2s

1 2s 1 3, γ 5 3

65. f (s) 5 s

1 2s 2 7, γ 5 5

66. f (s) 5 πs 2 cos (πs/2), γ 5 π

67. f (s) 5 (s

1 1) /(s

1 1), γ 5 3/2

68. f (s) 5 s1e

, γ 5 1

69. f (s) 5 s ln (s), γ 5 0

70. f (s) 5 s 1 log

(s), γ 5 11

71. f (s) 5 log

(s) 1 log

(s), γ 5 9

72. Suppose that f is differentiable and invertible, that P 5

(2, 3) is a point on the graph of f, and that the slope of the

tangent to the graph of f at P is 1/7. Use this information

to ﬁnd the equation of a line that is tangent to the graph

of y 5 f

(x).

73. If f (x) 5 4e

x21

1 3ln(x) for x . 0, then what is ( f

)

(4)?

c In each of Exercises 7479, use logarithmic differentiation

calculate the derivative of the given function. b

74. sin

(x)

75. x

ln (x)

76. ðx

11Þ

ðx

11Þ

77. log

(x)

78. sin

cos (x)

(x)

79. ln(x)

ln(x)

80. Show that there is a value c such that the tangent lines to

the graphs of y 5 e

and y 5 ln (x)at(c, e

) and (c,ln(c))

are parallel.

81. Suppose that f :(a, b) - (c, d) and g :(c, d) - (α, β) are

invertible. Prove that g 3 f is invertible. Derive a formula

for ((g 3 f)

)

in terms of f

and g

82. Suppose that u and υ are differentiable functions with

u(x) . 0 for all x.Letf (x) 5 u(x)

υ(x)

. Find a formula for

(x).

83. The invertible function f : [1,N) - [0,N) deﬁned by

f (s) 5 s ln (s) 2 s 1 1 is used in statistical physics for esti-

mating entropy. Find c and γ with f (c) 5 γ so that s 5

(t 2 γ) 1 c is a tangent line to the graph of s 5 f

(t)in

the ts-plane.

84. At time t, the bloodstream concentration C(t)ofan

intravenously administered drug is

CðtÞ5

ð1 2 e

2βt

Þð0 # tÞ

for positive constants α and β.

a. Given that the dimension of C is mass/volume, and an

exponential is unitless with unitless argument, what

are the dimensions of the constants β and α?

b. By comparing C(s) with C(u) for s , u, show that the

concentration of the drug is increasing.

c. What is the horizontal asymptote of the graph of

y 5 C(t) in the ty-plane?

d. What are the domain and image of C?

e. Suppose that the range of C is the image of C. Then C

is invertible. Describe C

completely by stating its

domain, stating its range, and giving an explicit for-

mula for C

(s). (Note: The roles of s and t in this

application are reversed from the discussion of

inverses in this section. That is because it is suggestive

to denote time by t, and time is the variable of the

function being inverted.)

f. Calculate C

(t) and (C

)

(s).

85. According to Fick’s Law, the diffusion of a solute through

a cell membrane is described by

cðtÞ5 C 1 ðcð0Þ2 CÞexpð2kAt=VÞ 0 # t , N:

Here c(t) is the concentration of the solute, C is the

concentration outside the cell, A is the area of the cell

membrane, V is the volume of the cell, and k is a positive

constant. Suppose that C , c(0).

a. Given that the dimensions of C and c(t) are both mass/

volume, and an exponential is unitless with unitless

argument, what is the dimension of the constant k?

b. Show that c ( t) is increasing on [0,N)ifc(0) , C. Show

that c(t) is decreasing on [0, N)ifc(0) .C.

c. What is the horizontal asymptote of the graph of

y 5 c(t) in the ty-plane?

d. What

are the domain and image of c?

e. Suppose that the range of c is the image of c. Then c is

invertible. Describe c

completely by stating its

domain, stating its range, and giving an explicit for-

mula for c

(s). (Note: The role reversal of s and t is

discussed in Exercise 84e.)

f. Calculate c

(t) and (c

)

(s).

86. An object is dropped from a height h. At time t, its height

is y(t), and its velocity is υ(t) 5 y

(t). If air resistance is

κυ(t)

for a positive constant κ, then

yðtÞ5 h 1 t

ﬃﬃﬃ



1 1 e

ﬃﬃﬃﬃ

gκ



a. Show that

υðtÞ52

ﬃﬃﬃ



1 2 expð2 2t

ﬃﬃﬃﬃﬃﬃ

gκ

1 1 expð2 2t

ﬃﬃﬃﬃﬃﬃ

gκ



3.6 Derivatives of Inverse Functions 229

b. Calculate the terminal velocity, lim

t-0

υðtÞ:

c. Verify that υ

(t) 52g1κυ(t)

d. Show that υ(t) 52

ﬃﬃﬃﬃﬃﬃﬃﬃ

g=κ

tanh ðt

ﬃﬃﬃﬃﬃﬃ

gκ

Þ. (See Exercise

73, Section 3.4.)

87. If the number q of units of an ordinary product that are

sold at price p is denoted by f ( p), then f is a decreasing

function of p. This relationship between p and q is known

as the Law of Demand. From it, we may infer that price is

a function of demand: p 5 f

(q). The graph of

p 5 f

(q) in the qp-plane is said to be the demand curve.

The elasticity of demand at price p is deﬁned to be E

( p) 52p  f

( p)/f ( p). Express the equation of the tan-

gent line to the demand curve at the point (q

, p

)in

terms of q

, p

, and E( p

Calculator/Computer Exercises

c In each of Exercise 8891, a point γ is given, as well as a

function f that is invertible on an open interval containing

c 5 f

(γ). Approximate ( f

)

(γ). b

88. f (s) 5 2s1

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

ﬃ

1 1

; γ 5 4

89. f (s) 5 s

1 2s 1 sin (s), γ 5 1

90. f (s) 5 s

2 2, γ 5 1

91. f (s) 5 s

1 4s 2 2, γ 5 15

c In Exercises 9295, a function f and

its domain are given.

Graph x 5 f

(y) in the yx-plane. (Do not attempt to ﬁnd a

formula for f

. Recall that a procedure for graphing an

inverse function has been described in Section 1.5.) Find the

equation of the tangent line to the graph of x 5 f

( y)at

(2, f

(2)). Add the graph of the tangent line to your plot. b

92. f (x) 5 2x

1 3x,0# x # 1

93. f (x) 5 11x exp (x)/2, 21 # x # 1.25

94. f (x) 5

ﬃﬃﬃ

1 3lnðxÞ; 1/2 # x # 2

95. f (x) 5 sin

(x) 2 cos (x) 1 2.6, 0 # x # 2

96. Approximate the value c such that the tangent lines to

the graphs of y 5 e

and y 5 ln (x)at(c, e

) and ( c,ln(c))

are parallel. Illustrate with a graph of the two functions

and their tangent lines.

97. Graph y 5 10

(ln (x 1 10

) 2 ln(x 2 10

))/2 for 0.1 #

x # 10. Add the graph of y 5 1/x to the same viewing

window. Which differentiation rule is illustrated?

3.7 Higher Derivatives

The derivative of a function is itself a function. For example, the derivative of the

function

pðtÞ5 t

2 5t

1 7

ðtÞ5 3t

2 10t:

The function p

is differentiable, so we may consider its derivative ( p

)

(t) 5 6t 2 10.

We simplify the notation by writing p

for ( p

)

. Of course the second derivative p

is also a function, and we may differentiate it to obtain the third derivative

pwðtÞ5 6:

This procedure may be carried on indeﬁnitely: The derivative of the (k 2 1)

derivative is called the k

derivative. However, writing more than two or three

primes becomes tedious, and it is even more tedious to read. So we have other ways

to write the higher derivatives.

Notation for Higher

Derivatives

DEFI NITION

The derivative of f

is called the second derivative of f. In general,

the derivative of the (k 2 1)

derivative of f, if it exists, is called the k

deri-

vative. We write the k

derivative of f as

00

ðk primesÞ or f

ðkÞ

f or D

ðf Þ:

230 Chapter 3 The Derivative

Sometimes you will see roman numerals used. For example, f

(iv)

might be used

instead of f

(4)

. The number k is called the ord er of the derivative f

(k)

.To

distinguish f

from higher order derivatives, we often call f

the ﬁrst derivative of

f. The function f itself is sometimes called the zeroeth derivative of f. When the

notation f

(k)

is used, it is important to include the parentheses, for f

has

already been deﬁned to be the k

power of f.

⁄ EX

AMPLE 1 Deﬁne p(x) 5 5x

2 8x

2 7x 2 11. Find p

(3)

(4).

Solution We

have, in order,

ð1Þ

ðxÞ5 20x

2 16x 2 7; p

ð2Þ

ðxÞ5 60x

2 16; p

ð3Þ

ðxÞ5 120x:

Therefore p

(3)

(4) 5 480. ¥

INSIGHT

Notice that, when we calculate a higher derivative, we do not substitute

in a value for x until we are ﬁnished differentiating. If you substitute in the value of x

too soon, then you end up with a constant function, and the next derivative will be 0.

When f is a function and f

(1)

(c), f

(2)

(c), ... ,f

(k)

times differentiable at c. Suppose that f is two times differentiable at c. This means

that f

ðcÞ and f

is differentiable at c.

According to the deﬁnition of the derivative, this means that the function f

deﬁned on an open interval centered at c. Thus hidden in this deﬁnition is the

requirement that f is not only differentiable at c but also on an open interval

centered at c. Similarly, if f is k times differentiable at c, then f, f

, ... ,f

(k21)

must

be differentiable in an open interval centered at c.

Velocity and

Acceleration

If p is position, and t is time, then υ (t) 5 p

(t) is the rate of change of position with

respect to time, or velocity (as in Section 3.1). The rate of change of velocity

with respect to time is acceleration a(t). Thus a(t) 5 υ

(t) 5 p

(t): accelerat ion is the

ﬁrst derivative of velocity with respect to time and the second derivative of position

with respect to time.

⁄ EX

AMPLE 2 If position (measured in feet) at time t (measured in seconds)

is given by p(t) 5 tan (t) for small values of t, then ﬁnd the acceleration at time

t 5 0.01 seconds.

Solution We

compute





sec

tðÞ 5

ð3:5:3Þ

2secðtÞ



secðtÞ



5 2secðtÞðsecðtÞtanð tÞÞ5 2sec

ðtÞtan ðtÞ:

At time t 5 0.01, we have

að0:01Þ5



0:01

5 2 sec

ð0:01Þ tanð0:01Þ0:0200027 ft=s

: ¥

3.7 Higher Derivatives 231

Newton’s Notation Yet another notation for higher derivatives is due to Newton. If p(t) is a function of

the time variable t, then the ﬁrst and second derivatives are represented by

p(t) and

€

p(t), respectively. This notation is often used in phy sics and engineering.

⁄ EX

AMPLE 3 An arrow is shot straight up. Its height at time t seconds is

given in feet by the formula H(t)5216t

1 160t 1 5. Compute its velocity and its

acceleration. Discuss the physical signiﬁcance of these quantities.

Solution The

velocity is υ (t ) 5

H(t) 5232t 1 160 ft/s. The acceleration is a(t) 5

€

H(t) 5232 ft/s

. Some interesting physical data may be read from this information.

For instance, when the arrow reaches its maximum height, then, at that instant,

it has neither upwar d nor downward motio n: Its velocity is zero. We solve

0 5

H(t) 5232t 1 160 to obtain that the maximum height occurs when t 5 5. At

this time, the height is H(5) 5 405 feet. Notice that at that time, the acceleration is

232 ft/s

—the acceleration is constantly equal to this value—but the velocity is

equal to zero.

INSIGHT

Although one can compute second, third, fourth, and higher derivatives,

the physical signiﬁcance of these quantities is increasingly difﬁcult to understand. It turns

out that, in some areas of engineering, the third derivative is useful: It is called jerk (and

the terms jolt, surge, and lurch have also been used). When you are in an elevator that is

not working properly, and your stomach feels as if it were left behind on the previous

ﬂoor, then you are experiencing jerk. In the past, engineers have built “jerkmeters” in

order to subject space vehicles to vibration tests. No term for the rate of change of jerk,

the fourth derivative of position, is in widespread usage, although jounce has been

suggested.

Approximation of

Second Derivatives

Higher derivatives can also be approximated by difference quotients. We will

illustrate the procedure by approximating the second derivative. We start by

writing f

(c)as(f

)

(c). We can approximate ( f

)

quotient D

)(c, h)off

(as discussed in Section 3.3). Thus

ðcÞ

ðc 1 h=2Þ2 f

ðc 2 h=2Þ

Next, approximat e f

(c 1 h/2) and f

(c 2 h/2) by the central difference quotients

f (c 1 h/2, h)andD

f (c 2 h/2, h):

ðcÞ

f ðc 1 hÞ2 f ðcÞ

f ðcÞ2 f ðc 2 hÞ

;

ðcÞ

ðf ðc 1 hÞ2 f ð cÞÞ2 ðf ðcÞ2 f ðc 2 hÞÞ

: ð3:7:1Þ

This is the second central difference quotient approxi mation to f

(c). The algebraic

simpliﬁcation

ðcÞ

f ðc 1 hÞ2 2f ðcÞ1 f ðc 2 hÞ

232 Chapter 3 The Derivative

may also be used, but, because the number f (c1h)1f (c2h) is very close to 2f (c )

when h is small, the subtraction can result in a loss of signiﬁcant digits. Therefore

the second central difference quotient approximation must be implemented

with care.

⁄ EX

AMPLE 4 The height of an object propelled upwards from ground level

is approximately

f ðtÞ5 33:33 ln ð54:25 cos ð0:5424t 2 1:552ÞÞm for 0 # t # 2 :862 s:

Estimate the acceleration of the object at time t 5 2.

Solution We

are asked to approximate f

f (t) is based on an approximation, using the differentiation rules of calculus to

obtain an “exact” value of f

(2) would suggest an accuracy that cannot be

obtained.) Figure 1 is a screen capture of a Maple session. In the ﬁrst line, the

second central difference quotient has been deﬁned and named D2. In the next

line, f has been deﬁned. The third line sets the number of digits used in the

computations to 15 to help guard against loss of signiﬁcance (Section 1.1). The

fourth line evaluates the second central difference quotients that correspond to

h 5 0.01, 0.001, . . . , 0.00000001. The ﬁrst four values of h indicate that f

(2) 

212.3. The two smallest values of h,10

and 10

, result in wildly inaccurate

approximations due to loss of signiﬁcance. We conclude that f

(2) 212.3. (The

negative sign indicates that the object is decelerating, as we would expect). The last

line of the Maple session evaluates f

(2) using the derivative rules of calculus. The

result conﬁrms our numerical approximation.

Leibniz’s Rule The Product Rule tells us how to compute the ﬁrst derivative of a product f g.In

1695, Leibniz derived a rule for computing higher derivatives of a product.

Leibniz’s Rule tells us how to calculate ( f g)

(n)

ðcÞ, f

(c), ...,

(n)

(c), and g

(c), g

(c), ...,g

(n)

(c). For now, we will state Leibniz’s Rule only for

m Figure 1

3.7 Higher Derivatives 233

second derivatives. Exercise 62 explains the general rule and asks you to verify it

for n 5 2.

THEOREM 1

Leibniz’s Rule for Second Derivatives. If f and g are 2 times

differentiable at c, then so is f g and

ðf  gÞ

ðcÞ5 f

ðcÞgðcÞ1 2f

ðcÞg

ðcÞ1 f ðcÞg

ðcÞ: ð3:7:2Þ

⁄ EX

AMPLE 5 A mass on a spring oscillates about its equilibrium position

according to the formula

xðtÞ5 e

2t=2

cosðt

ﬃﬃﬃ

Þcm

when t is measured in seconds. What is the acceleration of the mass at time t?

Solution Le

t f (t) 5 e

2t/2

, and g(t) 5 cos ðt

ﬃﬃﬃ

Þ: Then f

(1)

(t) 52e

2t/2

/2, f

(2)

(t) 5 e

2t/2

/4,

(1)

(t) 52

ﬃﬃﬃ

sin ðt

ﬃﬃﬃ

Þ; and g

ð2Þ

ðtÞ522 cos ðt

ﬃﬃﬃ

Þ: Thus



2t=2

cosðt

ﬃﬃﬃ



5 gðtÞf

ð2Þ

ðtÞ1 2f

ð1Þ

ðtÞg

ð1Þ

ðtÞ1 f ðtÞg

ð2Þ

ðtÞ

2t=2

cosðt

ﬃﬃﬃ

Þ1 2



2t=2





ﬃﬃﬃ

sin



ﬃﬃﬃ





2 2e

2t=2

cos ðt

ﬃﬃﬃ

2t=2

sin ðt

ﬃﬃﬃ

Þ2

2t=2

cos ðt

ﬃﬃﬃ

Þcm=s

: ¥

QUICK QUIZ

1. Calcul ate

expðx

Þ:

2. Suppose that a(t) is acceleration, υ(t) is velocity, and p(t) is position. Correct

the following three equations by inserting appropriate differentiation symbols:

p(t) 5 υ(t), υ(t) 5 a(t), p(t ) 5 a(t).

3. What is

ð3x

1 11x

2 17x

Þ?

4. Use Leibniz’s Rule to calculate



cosðxÞ



Answers

1. 2(1 1 2x

)exp (x

)2.p

(t) 5 v(t), v

(t) 5 a(t), p

(t) 5 a(t)3.0

4. 2 cos (x) 2 4x sin (x) 2 x

cos (x)

EXERCISES

Problems for Practice

c In each of Exercises 126, an expression for f (x) is given.

Compute the ﬁrst, second, and third derivatives of f (x) with

respect to x. b

1. 5x

2 6x 1 7

2. 4x

2 7x

3. 1/x

4. x

7/3

5. ln (x)

6. x ln (x)

ﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃﬃ

6x 1 5

8. 2

9. cos (3x)

10. exp (2x)

11. exp (2x)

234 Chapter 3 The Derivative