Бормотов А.Н. Полимерные композиционные материалы для защиты от радиации

Подождите немного. Документ загружается.

Оптимизация структуры эпоксидных композитов повышенной плотности

121

Нет ничего практичней хорошей теории.

Роберт Кирхгоф

Всякая точная наука

основывается на приблизительности.

Бертран Рассел

4. ОПТИМИЗАЦИЯ СТРУКТУРЫ ЭПОКСИДНЫХ

КОМПОЗИТОВ ПОВЫШЕННОЙ ПЛОТНОСТИ

В настоящее время современное строительство для изготовления де-

талей, элементов зданий и сооружений остро нуждается в композиционных

строительных материалах, которые отличаются высокими эксплуатацион-

ными характеристиками. Кроме того, композиционные строительные ма-

териалы для защиты от радиации должны обладать некоторыми специфи-

ческими свойствами: высокой средней плотностью, наличием элементов с

большими атомными номерами,

отсутствием кристаллической решётки,

минимальным содержанием элементов, образующих долгоживущие нук-

лиды, и т.д. [3].

Наибольший практический интерес представляет возможность полу-

чения композиционных строительных материалов с высокими физико-

механическими и эксплуатационными свойствами при минимальных за-

тратах времени и материальных ресурсов. Решение этой задачи показано в

данной главе на примере создания эпоксидного композита повышенной

плотности.

При создании эпоксидных композитов в качестве связующего ис-

пользовали эпоксидно-диановую смолу марки ЭД-16, отверждаемую поли-

этиленполиамином (ПЭПА), в качестве заполнителя и наполнителя – раз-

личные фракции полиминерального отхода с плотностью 5100 кг/м

; в ро-

ли пластификатора выступало минеральное масло ММ, а модификаторами

служили ПАВ и некоторые органические жидкости [104].

Полимерные композиционные материалы (ПКМ) – искусственные

материалы сложной структуры, состоящие из полидисперсных наполните-

лей и заполнителей, полимерных материалов с резко различными свойст-

вами и приобретающие в результате такого сочетания комплекс новых

свойств, не присущих исходным

материалам [72].

Формирование структуры эпоксидных композитов повышенной

плотности осуществляли с использованием основных положений поли-

структурной теории, теории оптимального управления и методов систем-

ного анализа. Сущность полиструктурной теории состоит в представлении

Глава 4

122

материала полиструктурным, то есть в выделении в единой структуре мно-

гих взаимозависимых структур, прорастающих одна в другую (по принци-

пу “структура в структуре”). Выделение систем и подсистем, иерархия

критериев качества, оптимизация режимов формирования отдельных

структур в полиструктуры – все это и определяет рецептуру и технологию

изготовления композитов.

Согласно полиструктурной теории, в ПКМ

различают микрострукту-

ру и макроструктуру. Микроструктура образуется при совмещении дис-

персного наполнителя и вяжущего и играет роль связующего в полимерра-

створах. Свойства микроструктуры определяются процессами, протекаю-

щими на границе раздела фаз, вязкостью связующего, активностью и дис-

персностью наполнителя, степенью наполнения, наличием ПАВ и т.д.

Макроструктура образуется при совмещении связующего (

микрострукту-

ры) и заполнителей. Свойства макроструктуры в значительной мере опре-

деляются степенью наполнения ПКМ.

Ввиду того, что свойства ПКМ определяются совокупностью свойств

микро- и макроструктуры, с точки зрения практической технологии доста-

точно рассмотрение общей структуры ПКМ на уровнях микроструктуры,

присущей связующим, и макроструктуры, характерной для композита в

целом [72]. Поэтому в данной

работе окончательный результат складывал-

ся из двух этапов: на первом этапе оптимизировали полимерную матрицу и

полифракционную смесь наполнителей и заполнителей, а на втором – их

совмещение с целью получения оптимального композита для литьевой

технологии и технологии прессования.

Несмотря на многообразие объектов и целей, оба этапа содержат

требование о доказательном выборе в

ограниченных пределах наиболее

целесообразного варианта инженерного решения, то есть представляют со-

бой задачи оптимизации. Такой подход позволяет последовательно нахо-

дить неизвестные компоненты математической модели, получать макси-

мальные результаты при минимальных затратах времени и материалов,

опираясь на уже исследованные области композиционного материаловеде-

ния.

Для большинства реальных материаловедческих, рецептурно-

технологических и технико-экономических

задач целесообразно приме-

нять полиноминальные модели [73], поэтому в данной работе для описания

поведения системы использовали полиноминальные экспериментально-

статистические модели (ЭС-модели) вида

∑∑ ∑

=< =

ε++⋅+⋅⋅+⋅+=

iji

iiijiijiio

xbxxbxbbY

K ,

(4.1)

где b

, b

определяются как статистические величины в нормализо-

ванном виде по экспериментальным данным;

Оптимизация структуры эпоксидных композитов повышенной плотности

123

ε – случайная величина, учитывающая совокупность ошибок экспери-

мента.

Причём, учитывая точность приборов и инструментов, используемых

при проведении экспериментов, достаточно уравнения регрессии второго

порядка. При использовании уравнений более высоких степеней точность

оценок коэффициентов уравнений регрессии будет превышать точность

определения экспериментальных данных, и уравнение регрессии будет не-

адекватно при проверке по критерию Фишера

. Исходя из этого, в данной

работе применялись полные квадратичные ЭС-модели. Такие модели по-

зволяют производить полный регрессионный анализ, результатом которого

является решение оптимизационной задачи первого вида – определение

оптимальных условий функционирования системы при любом расходе ре-

сурса и второго вида – определение минимального количества расхода ре-

сурса для обеспечения требуемого уровня

показателя качества системы

[73].

4.1. Оптимизация полимерной матрицы

Для оптимизации полимерной матрицы был выбран девятиточечный

композиционный симметричный план ПФЭ 3

, имеющий высокую эффек-

тивность по критериям D, A, E и Q, который легко анализируется и позво-

ляет представить результаты графически. Его целесообразно применять

всегда, когда неизвестно направление поиска и нет жёстких ограничений

на ресурсы [74].

Используя имеющиеся литературные данные в качестве априорных,

были выбраны следующие факторы и интервалы их варьирования:

фактор X

– концентрация отвердителя ПЭПА, интервалы варьирования:

−=

⎧

⎨

⎪

⎩

⎪

130

018

фактор X

– температура прогрева образцов, интервалы варьирования:

−=

⎧

⎨

⎪

⎩

⎪

180

060

140

Расчёты коэффициентов уравнений регрессий, их оценок, довери-

тельных интервалов, проверки критериев Стьюдента и Фишера и т.д. про-

водили в соответствии с методикой, изложенной в [72]. После проведения

всех статистических расчётов было получено окончательное уравнение

регрессии

–

от массы смолы ЭД-16;

–

от массы смолы ЭД-16;

–

от массы смолы ЭД-16;

–

в течении 5 ч

сов.

–

в течении 5 ч

сов

;

–

в течении 5 ч

сов

;

Глава 4

124

1,51,102,17112 XXXXY ⋅⋅−⋅−⋅+= .

(4.2)

В натуральном виде уравнение (4.2) имеет вид

()

TCCTTCR ⋅⋅−⋅−⋅+= 1,51,102,17112,

жс

(4.3)

где R

сж

(С, Т) – предел прочности при сжатии ненаполненных образцов раз-

мером 20 × 20 × 20 мм;

С – концентрация ПЭПА в % – оптимизируемый фактор X

;

Т – температура прогрева в

С – оптимизируемый фактор X

После решения данного уравнения регрессии при помощи EURECA:

The Solver, Version 1.0 были получены следующие значения R

сж

(С, Т), С и

Т:

max

= 129,79 ≈ 130 ΜΠa – предел прочности при сжатии;

С = – 0,252 ≈ 15 % – концентрация отвердителя от массы смолы;

Т = 1 ≈ 80

С – температура прогрева изделий.

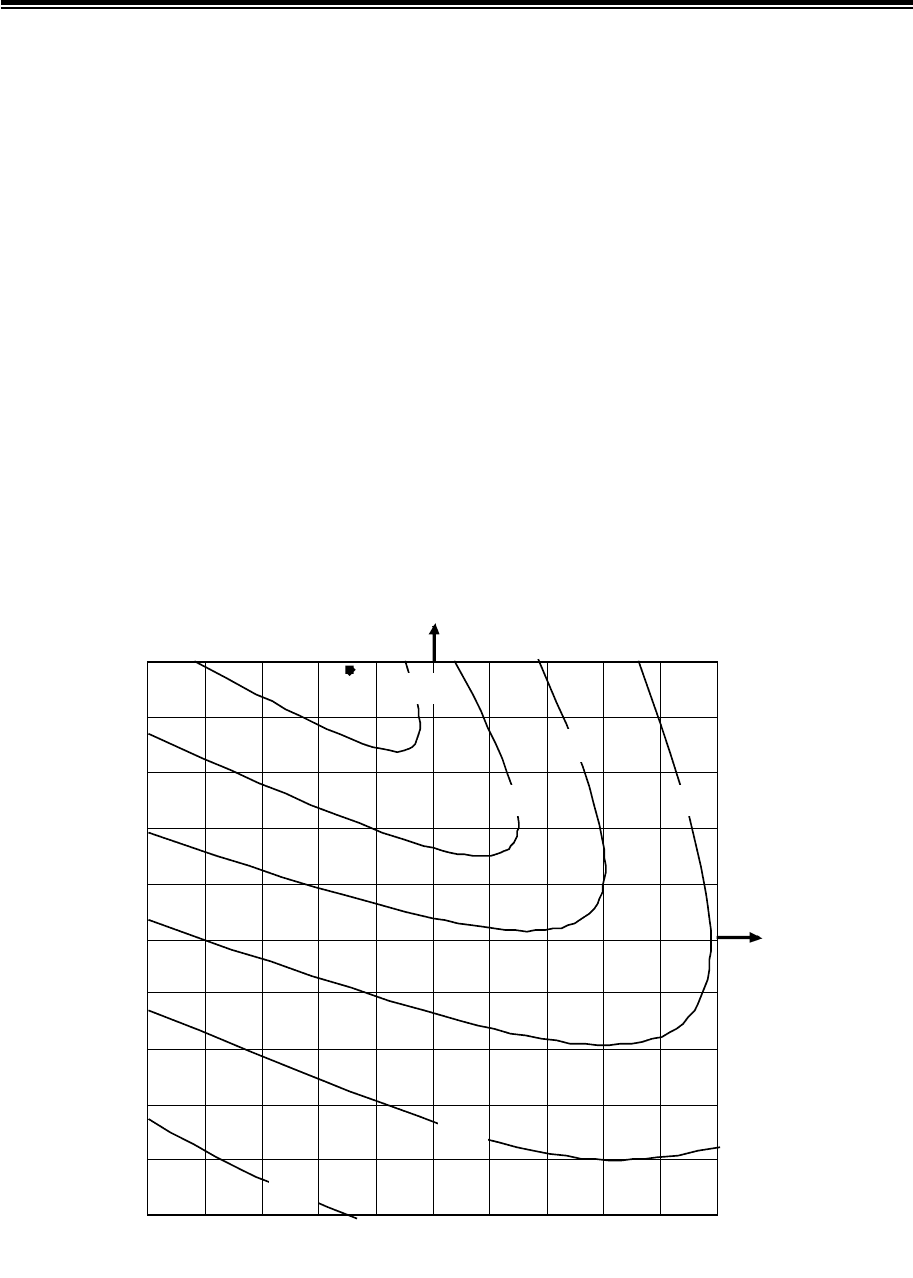
По этим данным была построена графическая зона эксперимента, на

которой отображены результаты оптимизации (рис. 4.1).

-1

-0,8

-0,6

-0,4

-0,2

0,2

0,4

0,6

0,8

-1 -0 ,8 -0,6 -0,4 -0,2 0 0,2 0,4 0,6 0,8 1

Max

- 0,8

- 1 - 0,6 - 0,4

- 0,2

0,2

0,4 0,6

0,8 1

0,8

0,6

0,4

0,2

- 0,2

- 0,4

- 0,6

- 0,8

- 1

120

125

115

110

105

100

Рис. 4.1. Изолинии прочности полимерной матрицы

Оптимизация структуры эпоксидных композитов повышенной плотности

125

Как видно из этого рисунка, уравнение (4.3) имеет чётко выражен-

ный максимум, соответствующий 15 %-ной (от массы смолы) концентра-

ции отвердителя и температуре прогрева изделий 80

С в течении 5 часов.

По частным производным от обеих переменных видно, что зависи-

мость прочности от температуры прогрева имеет прямо пропорциональ-

ный характер, а от концентрации отвердителя – параболический. Это мож-

но объяснить тем, что, увеличивая температуру прогрева, мы уменьшаем

размеры глобул трехмерной сетки и увеличиваем степень полимеризации

смолы, что приводит к

упорядочиванию структуры и улучшению физико-

механических свойств. Образующиеся в процессе твердения зародыши по-

лимерной фазы дисперсно распределены по объёму и фактически играют

роль наполнителей. Таким образом, твердеющие ненаполненные полимер-

ные системы на определённом этапе формирования структуры можно счи-

тать наполненными естественным образом. Учитывая, что на определён-

ном этапе твердения двухфазные

полимерные системы за счёт кластерооб-

разования стремятся достичь состояния термодинамического равновесия,

параболическая зависимость показывает существование такого количества

отвердителя, при котором появление зародышей полимерной фазы, их

самоорганизация – кластерообразование, а следовательно, достижение

термодинамического равновесия, происходит за самое короткое время и

протекает в самом полном объёме.

Глава 4

126

4.2. Подбор оптимального гранулометрического состава смеси

заполнителей

В ПКМ заполнители могут занимать до 80 % объёма и оказывают

определяющее влияние на свойства ПКМ. Поэтому подбор гранулометри-

ческого состава является одним из важнейших способов направленного ре-

гулирования свойств ПКМ.

Некоторые исследователи [21] предлагают использовать непрерыв-

ный фракционный состав заполнителей. Такой подход имеет ряд технико-

экономических преимуществ, однако в пустотах, образованных более

крупной

фракцией, при заполнении их более мелкой фракцией неизбежно

произойдёт раздвижка более крупных зёрен, что приведёт к увеличению

пористости и расхода связующего. При создании эпоксидных композитов

повышенной плотности для защиты от радиации такой подход неприем-

лем.

В работе [23] доказано преимущество прерывистой гранулометрии

перед непрерывным гранулометрическим составом.

В работе [75] установлено, что наибольший

упрочняющий эффект на

стекле ТФ-110 достигается при использовании дисперсного наполнителя с

удельной поверхностью 100 м

/кг при степени наполнения П:Н = 1:1.

Однако вопросы формирования макроструктуры в данной работе не изуча-

лись.

На сегодняшний день существует множество вариантов подбора гра-

нулометрического состава [21, 23, 67], что говорит об отсутствии у иссле-

дователей единого взгляда на данную проблему.

В данной работе при выборе факторов и их пределов варьирования

были использованы

рекомендации П.И. Боженова компоновать много-

фракционные смеси так, чтобы соотношение диаметров зёрен смежных

фракций было в пределах 1:4 – 1:5. При таком соотношении фракций мак-

симально возможный объём пустот, образуемый более крупной фракцией,

заполняется более мелкой фракцией практически без последующей раз-

движки зёрен. Поэтому в качестве факторов были выбраны следующие

фракции: X

= < 0,14 мм; X

= 0,315 – 0,63 мм; X

= 1,25 – 2,5 мм, соотно-

шение диаметров которых d

: d

= 4.

При выборе интервалов варьирования факторов X

, X

учитывали

то, что в природном состоянии в песках или в других сыпучих материалах

количество средних фракций в 1,5-2 раза больше, чем количество крупных

и мелких фракций. Такое же количественное соотношение было принято и

между фракциями X

, X

и X

При сплошном заполнении объёма, когда отдельные зёрна заполни-

телей касаются друг друга (непосредственно или через прослойки связую-

щего), дальнейшее уменьшение пустотности и сокращение расхода свя-

Оптимизация структуры эпоксидных композитов повышенной плотности

127

зующего в объёме возможно лишь за счёт размещения зёрен меньших раз-

меров в пустотах предыдущей фракции. Такое уплотнение структуры со-

провождается заметным упрочнением макроструктуры в результате увели-

чения числа контактов отдельных зёрен в объёме изделия. Поэтому спра-

ведливо предположить, что смесь, имеющая минимальную пустотность без

связующего, сохранит минимальную пустотность и после

совмещения с

полимерной матрицей. Исходя из этого предположения, достаточно опти-

мизировать гранулометрический состав по насыпной плотности.

Для проведения эксперимента был выбран симплекс-решётчатый

план второго порядка, позволяющий построить полное квадратичное урав-

нение регрессии вида

322331132112332211

XXAXXAXXAXAXAXAY ⋅⋅

⋅

+⋅

⋅+⋅= , (4.4)

где

, А

– статистические величины, определяемые по

экспериментальным данным;

⎩

⎨

⎧

301

155,0

– фракция < 0,14 как фактор математического плана;

⎩

⎨

⎧

361

285,0

– фракция 0,315 – 0,63 как фактор математического

плана;

⎩

⎨

⎧

201

105,0

– фракция 1,25 – 2,5 как фактор математического пла-

на.

Расчёты коэффициентов уравнения регрессии (4.4), функции диспер-

сии предсказания и проверка адекватности уравнения выполнены по при-

ложению II.5 [74].

Окончательное уравнение регрессии имеет вид

()

+⋅⋅

⋅

⋅+

⋅

=ρ

3121321321

5,02,09,789,787,7 XXXXXXXXXX

02,0 XX ⋅⋅+ .

(4.5)

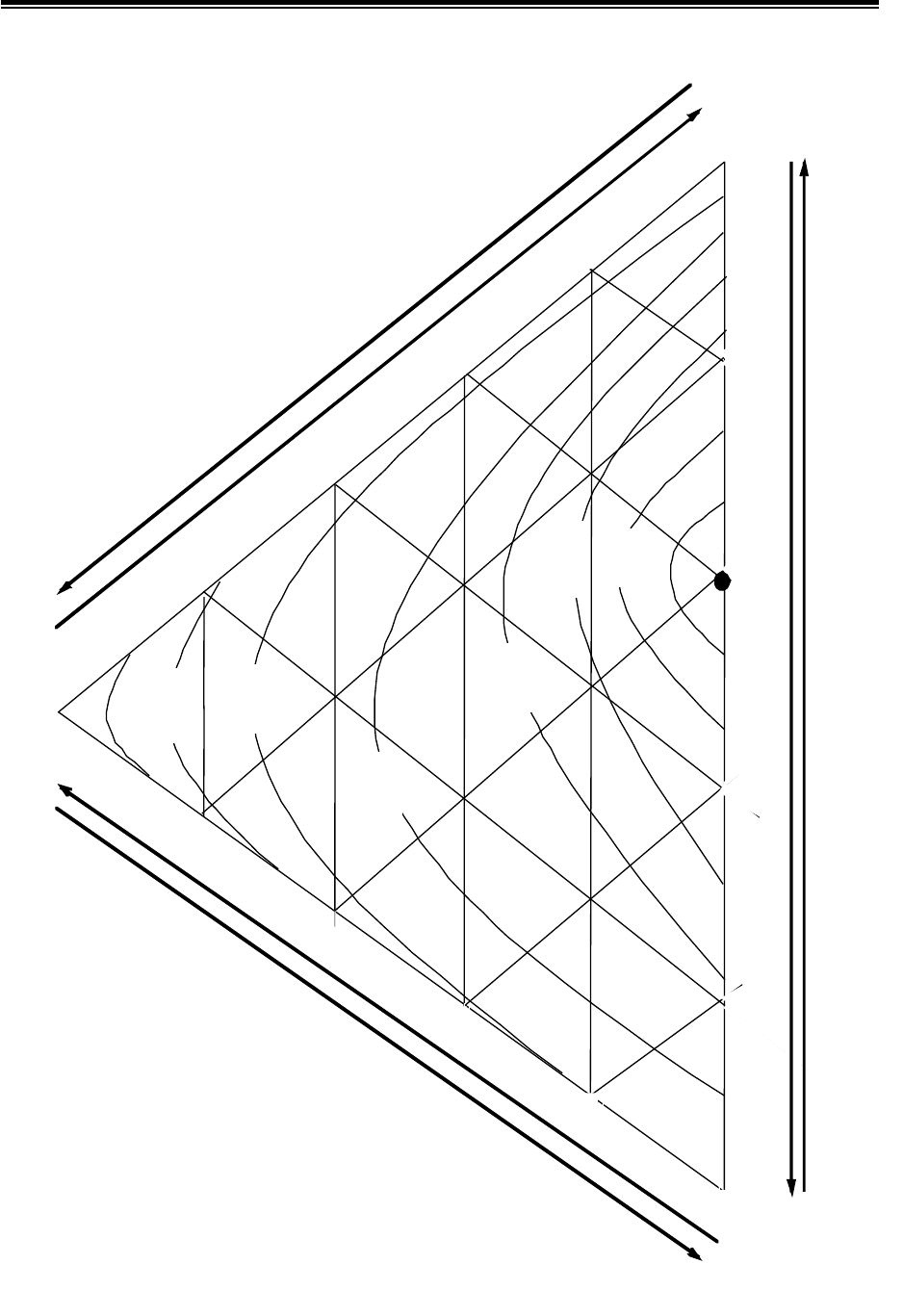
По уравнению (4.5) был построен концентрационный треугольник

Розенбома (рис. 4.2). Как видно из этого рисунка, оптимальное соотноше-

ние фракций наполнителя и заполнителя составляет

= 2:3 по объёму.

При этом фракция <0,14 мм выступает в качестве наполнителя, а фракция

1,25-2,5 мм – в качестве заполнителя. Отсутствие предполагаемой средней

фракции можно объяснить тем, что при свободной укладке зёрна средней

фракции, располагаясь между зёрнами крупной фракции, несколько раз-

двигают их, увеличивая пустотность смеси.

Глава 4

128

Рис. 4.2. Зависимость насыпной плотности от гранулометрического состава

0,13

0,16

0,19

0,22

0,25

0,28

3005

0,4

0,2

00,6

0,8

0,80,6

0,4

0,2 10

0,8

0,2

0,6

0,4

0,6

0,2

0,8

0,2

0,6

0,4

0,6

0,2

0,8

2700

2950

2900

2850

2800

2750

Оптимизация структуры эпоксидных композитов повышенной плотности

129

В идеализированной смеси, состоящей из шаровидных частиц одной

крупности, объём пустот, как известно, не зависит от размера частиц и из-

меняется в пределах от 47,6 до 25,9 % в зависимости от взаимного распо-

ложения частиц.

Пустотность реальных полифракционных смесей зависит от отноше-

ния размеров предыдущей и последующей фракций, а также от числа

фракций. По

данным [76, табл. 17], наименьшая пустотность реализуется

при двух фракциях с соотношением диаметров 1:16 и не превышает 16 %

(отношение

= 1:16).

Теоретическая максимальная насыпная плотность, рассчитанная по

уравнению (4.5), составляет 3005 кг/м

при пустотности 15,85 %, практи-

ческая максимальная насыпная плотность, полученная в ходе эксперимен-

та, равна 2995 кг/м

при пустотности 16 %. На основании этого в после-

дующих экспериментах использовали двухфракционную смесь с следую-

щим соотношением фракций: < 0,14:1,25-2,5 = 2:3.

Глава 4

130

4.3. Оптимизация структуры литьевых композитов

Макроструктура эпоксидных композитов формируется при совмеще-

нии полимерного связующего оптимального состава с плотной смесью за-

полнителей. Поэтому в последующих экспериментах использовали уже оп-

тимальную полимерную матрицу (рис. 4.1) и смесь заполнителей опти-

мального гранулометрического состава (рис. 4.2). Учитывая будущую об-

ласть применения эпоксидных композитов повышенной плотности, воз-

можно использование вибролитьевой технологии и технологии

прессова-

ния.

В соответствии с полиструктурной теорией, в наполненных ПКМ

выделяют структурные блоки, взаимодействующие через поверхности раз-

дела (контакта). Блоки скомпонованы из структурных блоков меньшего

размера, которые, в свою очередь, состоят из блоков более низкого струк-

турного уровня. Таким образом, непрерывность структуры ПКМ достига-

ется сложением дискретных элементов с повышенной

плотностью вещест-

ва в центре блоков и пониженной на периферийных участках – в областях

раздела [72]. Поэтому оптимизировать макроструктуру только по прочно-

сти или только по плотности будет недостаточно.

Методика

многокритериального синтеза эпоксидного композита

повышенной плотности для защиты от радиации подробно описана в гл. 2.

Сначала методами планирования эксперимента были получены ана-

литические зависимости средней плотности

ρ, кг/м

, и предела прочности

при сжатии

сж

, МПа [104].

Для этого был реализован девятиточечный композиционный план

ПФЭ 3

, в качестве откликов системы использовали данные плотности,

прочности и в дальнейшем отыскивали такие значения

и X

, при кото-

рых плотность и прочность были бы максимальны. При этом количество

модификаторов было определено ранее на ненаполненной смоле при со-

поставлении реологических кривых (см. гл. 3):

фактор

⎪

⎩

⎪

⎨

⎧

=−

250

501

X –

фактор

⎪

⎩

⎪

⎨

⎧

=−

2/11

7/10

12/11

X –

Расчёты коэффициентов уравнений регрессий, их оценок, довери-

тельных интервалов, а также проверки критериев Стьюдента и Фишера и

т.д. проводили в соответствии с методикой, изложенной в [73]. После про-

ведения всех статистических расчётов были получены окончательные

уравнения регрессий:

концентрация пластификатора ММ, в % от

массы смолы;

степень наполнения, П:Н по массе.