Бороденко В.А. Исследование систем управления в среде MATLAB

Подождите немного. Документ загружается.

231

вода только основной кривой, и команду Zoom on (-1,0), если не тре-

буется оценка устойчивости.

Для построения других частотных функций вычисляем в ли-

нейном диапазоне частот от 0 до 5 рад/с (200 точек) комплексный ко-

эффициент передачи системы wyr = tf(1.25, [1, 11, 60.5, 30.12, 15]).

>> f=linspace(0,5,200); % вектор частот в линейном масштабе

>> for ii=1:200

y(ii)=evalfr(wyr,0+j*f(ii)); % вектор комплексного отклика

end

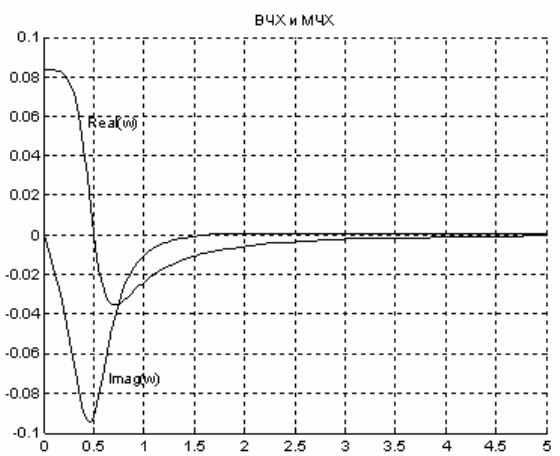
Совмещаем вещественную (синий цвет – ‘blue’) и мнимую

(красный цвет – ‘red’) характеристики на одном графике. Надписи на

графике Real(w) и Imag(w) добавлены в режиме редактирования фигу-

ры (рисунок 4.8).

>> hold on; % фиксируем графическое окно

>> plot(f,real(y),'b'); % выводим график ВЧХ синим

>> plot(f,imag(y),'r'); % выводим график МЧХ красным

>> title(‘ВЧХ и МЧХ’); grid; % выводим название и сетку

>> hold off % освобождаем графическое окно

Рисунок 4.8

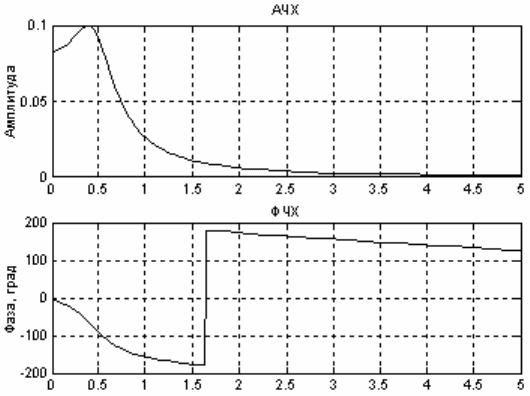
Строим в линейном масштабе амплитудную и фазовую характе-

ристики системы в двух окнах одновременно (рисунок 4.9).

>> subplot(2,1,1); % задаем первое окно

>> plot(f,abs(y)), grid; % рисуем АЧХ

>> title('АЧХ'); ylabel('Амплитуда'); % делаем подписи

232

>> subplot(2,1,2); % задаем второе окно

>> plot(f,angle(y)*180/pi), grid; % рисуем ФЧХ в градусах

>> title('ФЧХ'); ylabel('Фаза, град') % делаем подписи

Рисунок 4.9

Сходный результат можно получить, задав в окне Property

Editor: Bode Diagram на вкладке Units вывод абсолютных значений

амплитуды A(ω) absolute и отображение частоты в линейном масшта-

бе linear scale.

Приведем пример построения графика, на котором по оси абс-

цисс откладывается не частота, а ее десятичный логарифм, т.е. вели-

чина, измеряемая в декадах (рисунок 4.10). Кроме того, оба графика

совмещены в одном окне, что позволяет нагляднее установить вели-

чины ЛАЧХ при пересечении фазовой характеристики с линией -180

градусов, и ЛФЧХ на частоте среза (при L(ω) = 0). Поскольку легенда

здесь не выводит более одного пояснения, указание на характер линии

ЛФЧХ введено в поясняющую подпись правой оси ординат – оси

ЛФЧХ. Подписи к осям ординат необходимо делать в порядке индек-

сов (1 – левая, 2 – правая), вызывая их поочередно.

>> num=[3 2 1]; den=[1 2 3];

>> f=logspace(-2,2,100); y=freqs(num,den,f);

>> ly=20*log10(abs(y)); phi=angle(y)*180/pi;lf=log10(f);

>> clf

>> [haxes,hline1,hline2]=plotyy(lf,ly,lf,phi);

>> xlabel('w, декад'); title('ЛЧХ'); grid;

>> axes(haxes(1)); ylabel('ЛАЧХ, дБ');

>> axes(haxes(2)); ylabel('ЛФЧХ, град (пунктир)');

>> set(hline2,'linestyle','--','linewidth',2)

233

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2

-10

w, декад

ЛЧХ

ЛАЧХ, дБ

-2 -1.5 -1 -0.5 0 0.5 1 1.5 2

100

ЛФЧХ, град (пунктир)

Рисунок 4.10

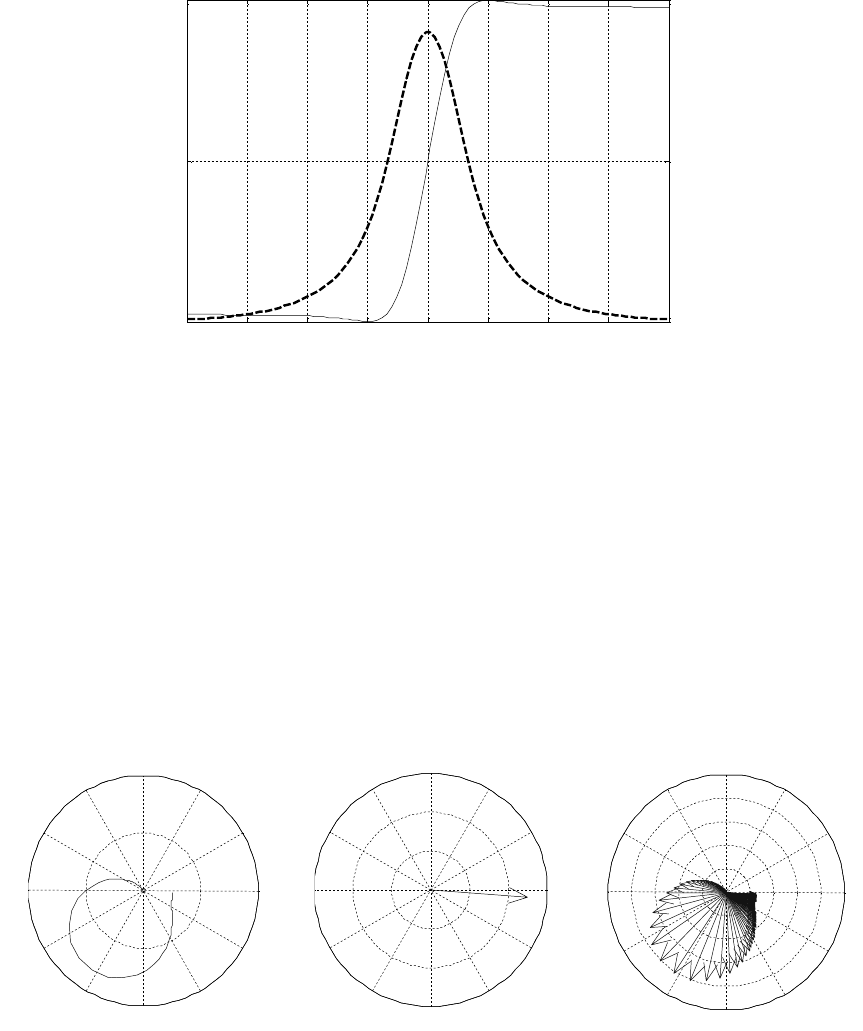
С помощью функций polar() и compass() можно построить в по-

лярных координатах АФЧХ (рисунок 4.11, а), один вектор с заданны-

ми амплитудой и фазой (рисунок 4.11, б) и всю совокупность векторов

для рассчитанных массивов амплитудной и фазовой характеристик

(рисунок 4.11, в).

>> y=freqs(5,[1 2 3 4]); mag=abs(y); phi=angle(y);

>> polar(phi,mag) % рисунок а

>> compass(y(1)) % рисунок б

>> compass(y) % рисунок в

2.5

210

240

270

120

300

150

330

180

0.5

1.5

210

240

270

120

300

150

330

180 0

210

240

270

120

300

150

330

180

а б в

Рисунок 4.11

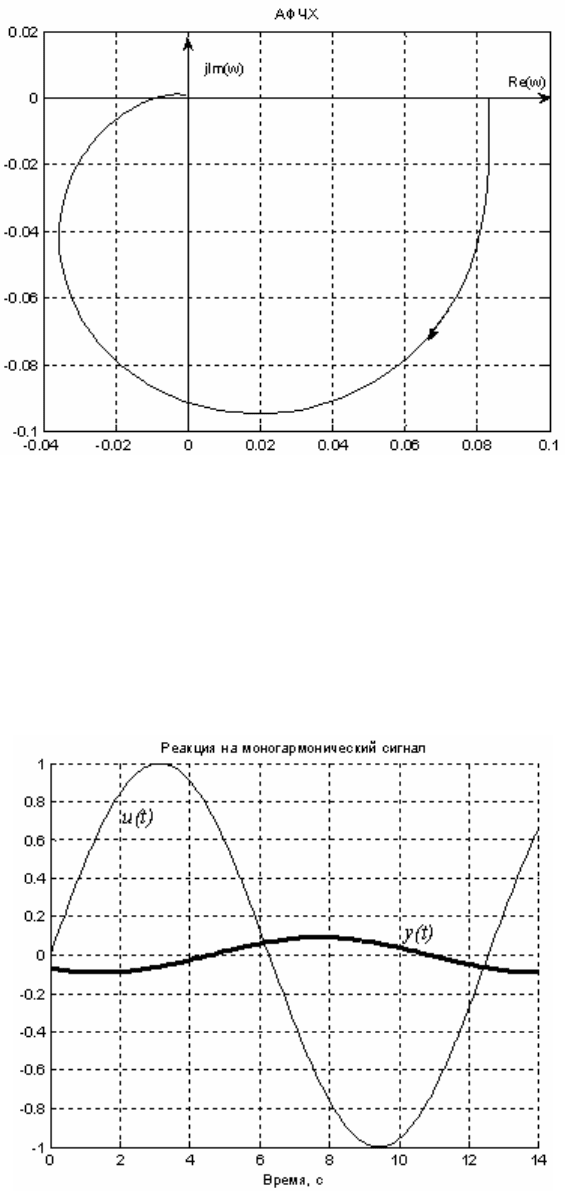
Амплитудно-фазовая частотная характеристика приводится на

рисунке 4.12, оси, надписи и стрелка на кривой добавлены в режиме

редактирования фигуры (учитывая комплексный характер отклика y,

можно было использовать более простую форму обращения plot(y)).

>> plot(real(y),imag(y)), grid; title ('АФЧХ')

234

Рисунок 4.12

При подаче на вход линейной системы моногармонического

сигнала отклик системы будет иметь ту же частоту ω, но отличаться

по амплитуде в M(ω) раз и по фазе на P(ω) радиан (градусов), где

M(ω) – это значение АЧХ, а P(ω) – значение ФЧХ при этой частоте.

Реакция на моногармонический сигнал с частотой 0,5 рад/с (рисунок

4.13) получена с помощью команд

Рисунок 4.13

>> x=evalfr(wyr,0+0.5i); % значение комплексного коэффициента

>> t=linspace(0,14,200); % время от 0 до 14 с (подобрано)

235

>> u=sin(0.5*t); % входной сигнал с частотой 0.5 рад/с

>> y=abs(x)*sin(0.5*t+angle(x)*180/pi); % выходной сигнал

>> hold on; plot(t,y,'r'); plot(t,u,'g'); grid; hold off;

>> title('Реакция на моногармонический сигнал');

>> xlabel('Время, с')

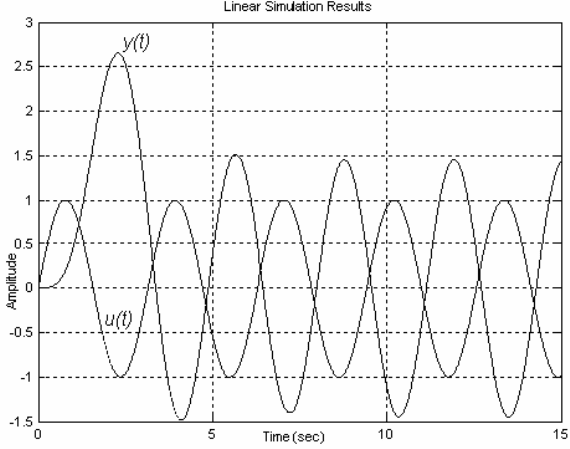
Выполним анализ частотной реакции y(t) системы на моногар-

монический сигнал u=A×sin(ω×t+φ), где для конкретного случая А = 1,

ω = 2 рад/с, а φ = 0°, в течение 15 с (рисунок 4.14).

>> w=tf(10,[1 2 3 1.4]);

>> t = 0:0.01:15; u = sin(2*t);

>> lsim(w,u,t)

Рисунок 4.14

Из графика видно, что в начальный момент имеет место пере-

ходный процесс, который затухает примерно через 7 с, после чего

можно определять параметры реакции системы на заданной частоте:

АЧХ, как отношение выходной амплитуды к входной, и ФЧХ, как

разность моментов наступления максимумов сигнала, отнесенную к

длительности периода и умноженную на 360 градусов.

Соответственно A(ω)= 1.45/1 = 1.45, φ(ω) = 1.7×360/3.2 = 191.25°

(с отставанием по фазе) или -168.75° (с опережением по фазе).

4.3 Оценка устойчивости линейных систем

Проще всего устойчивость системы позволяет оценить функция

isstable(имя_системы), возвращающая 1 (устойчива), 0 (неустойчива)

или NaN (обычно для FRD систем), например

236

>> w=tf([1 2 3],[1 2 3 4 1]);

>> isstable(w)

ans =

Рассмотрим далее стандартный набор приемов оценки устойчи-

вости системы.

Из физического признака устойчивости, требующего стремле-

ния с течением времени всех свободных составляющих переходного

процесса к нулю, вытекает, что у устойчивой системы установившееся

значение импульсной характеристики impulse() или реакции на нену-

левые начальные условия initial(sys,x0) должно стремиться к нулю.

Для полноты картины все элементы вектора начальных значений х0

следует задать ненулевыми, при этом неважно, как на самом деле

пронумерованы переменные состояния.

Математический признак устойчивости линейной системы тре-

бует, чтобы все корни характеристического уравнения имели отрица-

тельную действительную часть (все полюса системы были левыми).

Применим для расчета корней полинома функцию roots().

>> D=[1 2 3 4 2]; roots(D)

ans =

-0.0000 + 1.4142i

-0.0000 - 1.4142i

-1.0000 + 0.0000i

-1.0000 - 0.0000i

Представленная в примере система близка к колебательной гра-

нице устойчивости, поскольку ее характеристический полином D(s)

содержит корни с практически нулевой действительной частью при

остальных левых корнях (минус перед нулевой действительной ча-

стью корня говорит о том, что необходимо более точное исследование

устойчивости системы – по крайней мере, другой формат вывода).

В MATLAB корни характеристического полинома (полюсы сис-

темы) выводят также функции p = pzmap(sys), pole(sys), damp(sys) и

eig(sys), [r,p]=residue(num, den), [z,p]=tf2zp(num,den), p=rlocus(sys,0).

При проектировании бывает целесообразно определить диапа-

зон значений коэффициента усиления k, включенного последователь-

но с объектом в замкнутой системе регулирования, при котором сис-

тема сохраняет устойчивость.

Функция rlocus(имя_системы) производит расчет и вывод в гра-

фическое окно корневого годографа (Root Locus). Требования к ана-

лизируемой системе в этом случае аналогичны требованиям критерия

Найквиста, т. е. исходная система должна быть разомкнутой. Вычис-

237

ляются и отображаются на комплексной плоскости корни характери-

стического уравнения замкнутой системы D(s) = D

раз

(s) + k×N(s) при

изменении коэффициента k от нуля до бесконечности.

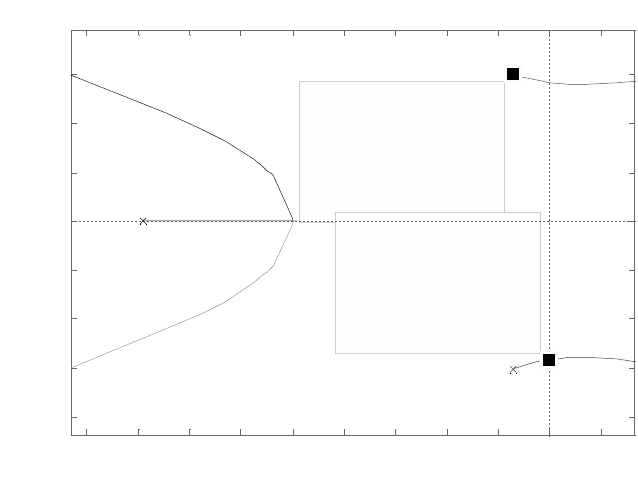
Из корневого годографа (рисунок 4.15) видно, что замкнутая

система теряет устойчивость при коэффициенте усиления Gain = 1.5 с

выходом полюсов на мнимую ось (действительная часть корня стре-

мится к нулю или становится положительной).

>> plant=tf(1,[1 2 3 4 0.5]); rlocus(plant)

Root Locus

Real Axis

Imaginary Axis

-1.8 -1.6 -1.4 -1.2 -1 -0.8 -0.6 -0.4 -0.2 0 0.2

-2

-1.5

-1

-0.5

0.5

1.5

System: plant

Gain: 0

Pole: -0.142 + 1.51i

Damping: 0.0937

Overshoot (%): 74.4

Frequency (rad/sec): 1.51

System: plant

Gain: 1.5

Pole: 0.000167 - 1.41i

Damping: -0.000118

Overshoot (%): 100

Frequency (rad/sec): 1.41

Рисунок 4.15

Функция [k,p]=rlocfind(sys,[p1 p2 ...]) находит значение коэффи-

циента k по заданному полюсу (полюсам) p1 замкнутой системы, если

последний достижим, и возвращает соответствующие ему полюсы p.

>> sys=tf(1,[1 2 3 4 0]);

>> [k,p]=rlocfind(sys,[0 0+1.4142i])

k =

0 2.0000

p =

0 0.0000 + 1.4142i

-1.6506 0.0000 - 1.4142i

-0.1747 + 1.5469i -1.0000 + 0.0036i

-0.1747 - 1.5469i -1.0000 - 0.0036i

Применение алгебраических критериев устойчивости Гурвица и

Рауса было показано ранее. Построение кривой Михайлова в MAT-

LAB не предусмотрено, однако для этого можно воспользоваться су-

238

ществующей функцией nyquist(). Кривая Михайлова строится с тем

отличием, что целесообразно самостоятельно подобрать диапазон час-

тот fr (в примере от 0 до 2 рад/с с шагом 0.1) и указать у дроби переда-

точной функции единицу в качестве знаменателя, поскольку вводится

только числитель, равный характеристическому полиному.

>> d=[1 2 3 4 1];

>> fr=0:0.1:2;

>> nyquist(d, 1, fr)

На графике следует убрать кривую при отрицательных частотах

(рисунок 4.16), для чего снять флажок в меню Show-Negative Frequen-

cies, и заменить заголовок в режиме редактирования фигуры Plot Edit.

-2 -1 0 1 2 3 4 5 6

-8

-6

-4

-2

Крив ая Михайлов а

Real Axis

Imaginary Axis

Рисунок 4.16

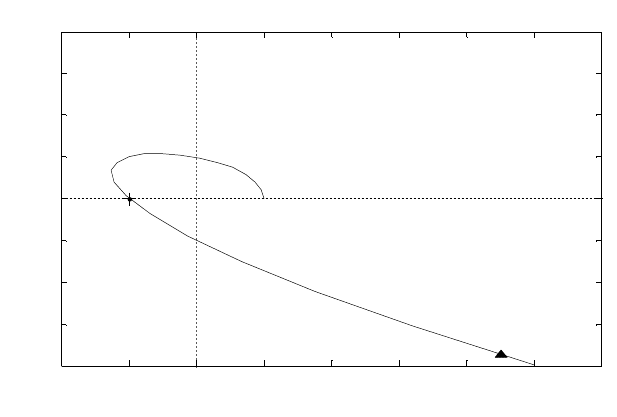
Аналогичный результат может быть получен без использования

функции nyquist(). Надпись к графику, оси и подписи к ним придется

делать самостоятельно, зато не будет креста в точке (-1,j0).

>> d=[1 2 3 4 1]; w=0:0.01:2; fr=0+j*w; h=polyval(d,fr);

>> plot(h),grid; title('Критерий Михайлова')

Описываемая далее функция uv() реализует критерий Михайло-

ва (вторую форму) путем вычисления коэффициентов четной и нечет-

ной функций и выводом (если указано в левой части выражения) их

корней, т. е. частот пересечения графиков U(ω) и V(ω) с осью абсцисс.

function [u,v,ur,vr] = uv(p)

% Критерий Михайлова – вторая форма

% Входной параметр - полином p, выходной - векторы U и V

239

n=length(p); pp=p; p=fliplr(p);

m=n-(n~=fix(n/2)*2);

k=0;kk=1;

for i=1:n

if k==2

k=0;kk=kk*(-1);

end

p(i)=p(i)*kk; k=k+1;

end

ut=[];vt=[];urt=[];vrt=[];

i=1:2:n; ut(i)=[ut,p(i)];

i=1:2:m; vt(i)=[vt,p(i+1)];

ut=fliplr(ut);vt=[fliplr(vt),0];

urr=roots(ut);vrr=roots(vt); % вычисление корней функций

mur=(real(urr)>=0 & imag(urr)==0); % выбор действительных частот

mvr=(real(vrr)>=0 & imag(vrr)==0);

for i=1:length(urr) % формирование вектора частот четной функции

if mur(i)==1

urt=vertcat(urt,urr(i));

end

for i=1:length(vrr) % формирование вектора частот нечетной функции

if mvr(i)==1

vrt=vertcat(vrt,vrr(i));

end

if nargout==0 % проверка необходимости строить график

w=0:0.01:(max([urt vrt])*1.1); % до максимальной частоты

f=0+j*w; h=polyval(pp,f);

plot(w,real(h),w,imag(h),'--',w,0,'k.-'), grid;

title('Критерий Михайлова (форма 2)');

xlabel('Частота, рад/c'); legend boxoff; % без рамки

legend('U(w)','V(w)','location','best') % выбрать место

else

u=ut;v=vt;ur=urt;vr=vrt; % только вывод полиномов и частот

end

Результатом обращения к этой функции с указанием выходных

аргументов (слева от знака равенства) будет вид четной и нечетной

функций, представленных коэффициентами, и их корни (частоты)

>> den=[1 2 3 4 5]; [u,v,ur,vr]=uv(den)

u =

1 0 -3 0 5

v =

-2 0 4 0

ur =

[]

240

vr =

1.4142

откуда видно, что частот пересечения графиков с осями только две,

это 0 и 1.4142 (при построении частотных характеристик мнимые,

комплексные и отрицательные частоты должны отбрасываться, что и

делает разработанная функция), причем обе принадлежат нечетной

функции V(ω). Средствами MATLAB можно придать стандартный вид

четной и нечетной функциям, используя символьную переменную 'w'.

>> u=poly2sym(u,'w')

u =

w^4-3*w^2+5

>> v=poly2sym(v,'w')

v =

-2*w^3+4*w

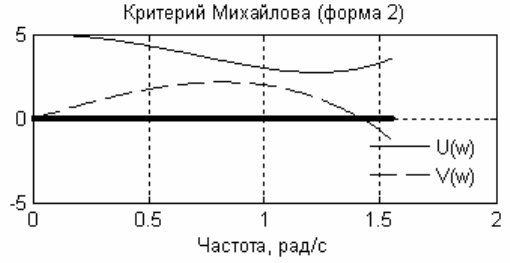
График (рисунок 4.17), построенный с помощью этой же функ-

ции, но при обращении без выходных аргументов, подтверждает сде-

ланные выводы – система неустойчива, так как отсутствует поочеред-

ное пересечение характеристиками оси частот (чередование корней).

Рисунок 4.17

Универсальная функция nyquist() может использоваться также

для оценки устойчивости методом D-разбиения по одному параметру.

При этом в качестве аргумента функции задают отношение полино-

мов от s, получающееся после разрешения характеристического урав-

нения относительно исследуемого параметра, либо задают в знамена-

теле 1. Приведем пример исследования влияния на устойчивость сис-

темы коэффициента усиления k, входящего в характеристическое

уравнение

D(s)=1.6s

+8.928s

+11.908s

+10.22s+87.4+(1.04s

+1.67s

+2.2s+1.8)k=0.

Разрешая уравнение относительно k, получаем дробь