Бороденко В.А. Исследование систем управления в среде MATLAB
Подождите немного. Документ загружается.

301
c =
x1 x2 x3
y1 0 1 10
d =
u1
y1 0
Результаты можно проверить, вычислив собственные значения
замкнутой системы (корни характеристического уравнения) и ее пере-
даточную функцию.
>> eig(sysp)
ans =
-1.0000 + 1.0000i
-1.0000 - 1.0000i
-1.0000
>> tf(sysp)
Transfer function:
0.2 s + 2
---------------------
s^3 + 3 s^2 + 4 s + 2
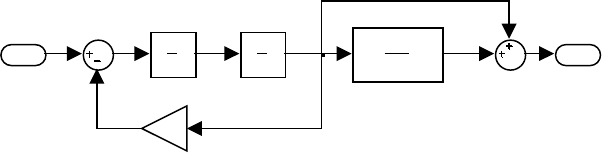
Рассмотрим вычисление матрицы k коэффициентов обратной
связи по переменным состояния модального регулятора для произ-
вольно заданного объекта (рисунок 4.70) при включенном в замкну-
тый контур обратной связи блоке с коэффициентом регулятора К, в
том числе для случая измерения только выходной переменной.
>> a=[-1 1 0;0 0 1;0 -3 0]; % самостоятельно описываем объект
>> b=[0 0 1]'; c=[1 1 0]; d=0;
1
y
1
s+1
Transfer Fcn
1
s
Integrator1
1
s
Integrator
3
Gain
1
u
x3 x2 x1
Рисунок 4.70
>> sys=ss(a,b,c,d); % строим его модель в пространстве состояний
>> w=tf(sys) % вычисляем передаточную функцию объекта
Transfer function:
s + 2
-------------------
s^3 + s^2 + 3 s + 3
>> [num,den]=tfdata(w,'v');
302
>> DD=poly(a) % характеристический полином разомкнутой системы
DD =
1.0000 1.0000 3.0000 3.0000
>> [ac,bc,cc,dc]=tf2ss(num,den) % матрицы канонической формы
ac =
-1.0000 -3.0000 -3.0000
1.0000 0 0
0 1.0000 0
bc =
1
0
0
cc =
0 1 2
dc =
0
>> sysc=ss(ac,bc,cc,dc); % модель объекта в канонической форме
>> v=[-10,-1+i,-1-i]; % вектор с желаемым расположением полюсов
>> D=poly(v)
D =
1 12 22 20 % новый характеристический полином
>> K=D(end)/cc(end) % находим коэффициент усиления регулятора К
K =
10
>> k=(D-DD)/K
k =
0 1.1000 1.9000 1.7000
>> k=k(2:end) % матрица k коэффициентов обратной связи
k =
1.1000 1.9000 1.7000
>> Heq=tf(k,cc) % ПФ ПД-регулятора в цепи главной обратной связи
Transfer function:
1.1 s^2 + 1.9 s + 1.7
---------------------
s + 2
>> wh=feedback(w*K,Heq) % передаточная функция замкнутой системы
Transfer function:
10 s^2 + 40 s + 40
---------------------------------
s^4 + 14 s^3 + 46 s^2 + 64 s + 40
>> ww=minreal(wh) % главная ПФ после удаления лишних корней
Transfer function:
10 s + 20
------------------------
s^3 + 12 s^2 + 22 s + 20
303
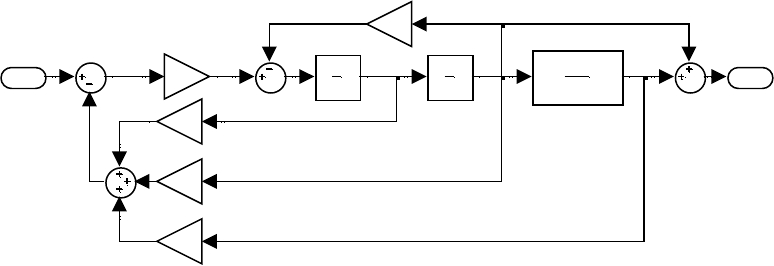
Получили систему с ПДД-регулятором в цепи главной обратной
связи (передаточная функция H
eq
(s)), обеспечивающую те же характе-
ристики (нулевую установившуюся ошибку, заданный вид полинома),
что и система с обратными связями по всем переменным состояния
(рисунок 4.71).
1
y
1.1
k3
0.8
k2
0.9
k1
10
K
1
s+1
3
1
s
2
1
s
1
3
1
r
x1x3 x2
u
Рисунок 4.71
Проверим это. Воспользовавшись матрицей преобразования Т,
найдем значения коэффициентов обратной связи системы в исходном
виде, подставим их в модель, созданную в среде Simulink и вычислим
числитель и знаменатель передаточной функции созданной системы.
>> kk=k*T % запишем вычисленные значения в блоки k1, k2, k3 модели
kk =
0.9000 0.8000 1.1000
>> [ne,de]=linmod('untitled') % получим ПФ модели без названия
Returning transfer function model
ne =
0 -0.0000 10.0000 20.0000
de =
1.0000 12.0000 22.0000 20.0000
На практике для измерения чаще всего доступна лишь выходная
переменная объекта y(t), поэтому для оценки неизмеряемых перемен-
ных состояния применяют специальное устройство – наблюдатель со-
стояния. В его основе лежит модель объекта управления в виде набора
интеграторов, охваченных прямыми связями с коэффициентами пере-
дачи b
0
... b
m
и обратными связями с коэффициентами передачи a
10
...
a
n0
.
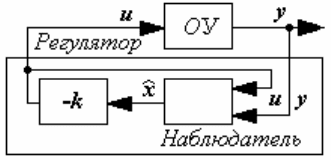
Функция reg(plant,k,L) помогает построить регулятор для задан-
ного в пространстве состояний полностью управляемого и наблюдае-
мого объекта регулирования plant, используя матрицу k обратных свя-
304
зей по оценкам переменных состояния
x
и матрицу L коэффициентов
передачи наблюдателя, входящего в состав регулятора (рисунок 4.72).
Рисунок 4.72
Обычно коэффициенты матрицы k выбираются с помощью
функции place() или LQG-проектирования для управляемого и наблю-
даемого объекта.
При стандартном описании объекта матрицами A, B, C, D про-
ектируемому регулятору соответствует набор матриц А
н
, b
н
, с
н
xcxk
bxALxkLDBLCAx
н
нн
u
yy
)(
Такой регулятор связан с объектом контуром положительной
ОС, поскольку минус содержится в матрице k – эта матрица будет на-
ходиться на месте матрицы с
н
наблюдателя. Размерность матрицы L
соответствует размерности матрицы В объекта, она и будет поме-
щаться на место матрицы b
н
наблюдателя: записываем в матрицу 1 на
месте х
3
, поскольку по правилам MATLAB переменные назначаются
от входа системы к выходу Полюсы наблюдателя должны обеспечи-
вать ускоренное затухание переходного процесса оценки переменных
состояния – задав желаемые значения полюсов матрицей А
н
и матрицу
L, можно получить необходимую матрицу k=(А–А
н
–LC)(B–LD)
-1
.
Сформируем объект регулирования plant и перейдем к его опи-
санию переменными состояния
>> plant=tf(1,[1 2 3 4]); plant=ss(plant);
>> [a,b,c,d]=ssdata(plant) % описание объекта SS-моделью
a =
-2.0000 -1.5000 -2.0000
2.0000 0 0
0 1.0000 0
b =
0.5000
0
0
c =
0 0 1
305
d =
0
>> v=roots([1 3 3 2]); % формируем вектор полюсов замкнутой системы
>> k=place(a,b,v) % вычисляем матрицу обратных связей как обычно
k =
2.0000 -0.0000 -2.0000
>> L=[0;0;1]; % задаем матрицу коэффициентов наблюдателя
>> compensator=reg(plant,k,L) % формируем регулятор по двум матрицам
a =
x1 x2 x3
x1 -3 -1.5 -1
x2 2 0 0
x3 0 1 -1
b =
u1
x1 0
x2 0
x3 1
c =
x1 x2 x3
y1 -2 3.997e-015 2
d =
u1
y1 0
Функция L = place(a',c',v).' возвращает матрицу коэффициентов
L наблюдателя, используя транспонированные матрицы А, С объекта
управления и вектор v желаемых полюсов замкнутой системы регули-
рования. Используя матрицу L, функция est = estim(sys,L) формирует
наблюдатель est с оценками выходной величины
y
и переменных со-
стояния
x
для полностью наблюдаемого объекта.
x
1
C
x
y
xCyLxAx
)(
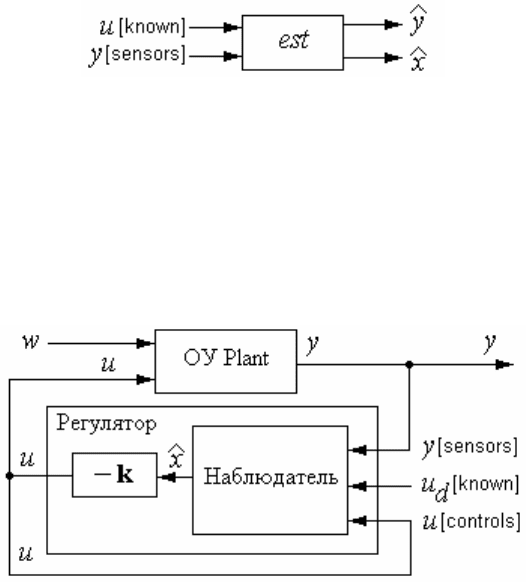
В форме est = estim(sys,L,sensors,known) проектируется наблю-
датель для объекта в общем виде, причем индексы в векторах sensors
и known указывают соответственно измеряемые выходы y и управ-
ляемые входы u (рисунок 4.73). Остаются неуправляемые входы w и
неизмеряемые выходы z, что описывается уравнениями системы
u
D
D
w
D
D
x
C
C
y
z
uBwBAxx
22
12
21
11
2
1
21
306
и уравнениями наблюдателя
u
D
x
1
C
x
y
uDxCyLuBxAx
0
)(
222
2222
Рисунок 4.73
В полном виде функция reg(plant,k,L,sensors,known,controls) тре-
бует указания индексов измеряемых выходов объекта в векторе sen-
sors, дополнительных входов объекта в векторе known и всех управ-
ляемых входов объекта в векторе controls (рисунок 4.74). Неуправляе-
мые входы w объекта соответствуют возмущениям, шумам.
Рисунок 4.74
В группу проектирования оптимальных регуляторов входят
функции kalman(), lqr(), lqry(), lqi(), lqg(), lqgreg(), lqgtrack().
Функция [kest,L,S]=kalman(sys,Qn,Rn,Nn) проектирует наблюда-
тель kest в виде фильтра Калмана при наличии шумов технологиче-
ского процесса w (на входе объекта sys) и измерений v (на выходе дат-
чиков) и шумами ковариаций E(ww
T
)=Q, E(vv
T
)=R, E(wv
T
)=N, возвра-
щая также матрицу коэффициентов L и решение уравнений Риккати
S.
Функции lqg(), lqgreg(), lqgtrack() позволяют проектировать ли-
нейно-квадратичный гауссов регулятор LQG. Функции lqr(), lqry(),
lqi() предназначены для синтеза линейно-квадратичного регулятора с
оптимизацией соответственно по переменным состояния, по выходам
и с добавочным интегратором.
Функция [k,S,e]=lqr(sys,Q,R,N) или [k,S,e]=lqr(A,B,Q,R,N) рас-
считывает оптимальную матрицу коэффициентов обратных связей по
307
переменным состояния k = R
-1
(B
T
S + N
T
), минимизируя интегральную
квадратичную оценку
0
)2()( dtuJ
TTT
NuxRuuQxx
для объекта в пространстве состояний, заданного SS моделью sys или
матрицами А, В. Выводятся также решение S алгебраических уравне-
ний Риккати A
T
S+SA-(SB+N)R
-1
(B
T
S+N
T
)+Q = 0 и собственные значе-
ния замкнутой системы регулирования e = eig(A-Bk). Здесь и далее
неописанная матрица N считается нулевой.
Форма [k,S,e]=lqry(sys,Q,R,N) отличается тем, что при построе-
нии линейно-квадратичного регулятора функционал минимизируется
не по вектору состояния, а по выходному вектору системы
0
)2()( dtuJ
TTT
NuyRuuQyy
.
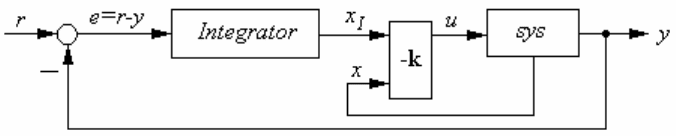
Регулятор, рассчитываемый функцией [k,S,e]=lqi(sys,Q,R,N), ис-
пользует дополнительно интегратор в контуре обратной связи (рису-
нок 4.75) и закон управления u = -k[x; x
I
], где переменная x
I
формиру-
ется на выходе интегратора. Для MIMO системы число интеграторов
равно размерности вектора выходов y.
Рисунок 4.75
Функция regs=lqgreg(kest,k) образует LQG регулятор из наблю-
дателя kest, рассчитанного функцией kalman(), и статической матрицы
коэффициентов обратной связи k, спроектированной заранее функ-
циями lqr(), lqry() или lqi(). Аналогичное назначение имеет функция
regi=lqgtrack(kest,k), отличаясь вводом интегральной составляющей в
закон регулирования u = -k[
x
; x
I
], наподобие lqi(). LQG регуляторы
соединяются с объектом всегда положительной обратной связью.
308
Литература
1 Бороденко В. А. Практический курс теории линейных систем
автоматического регулирования. – Павлодар : Кереку, 2007. – 260 с.
2 Лазарев Ю. Ф. MatLAB 5.x. – Киев : BHV, 2000. – 384 с.
3 Дьяконов В. MATLAB 6 : учебный курс. – СПб. : Питер, 2001.
– 592 с.
4 Дьяконов В., Круглов В. MATLAB. Анализ, идентификация и
моделирование систем. – СПб. : Питер, 2002. – 448 c.
5 Control System Toolbox 9. Getting Started Guide. – MathWorks,
2010. – 280 c.
6 Теория автоматического управления. – Под ред. Ю. М. Соло-
менцева. – М. : Высш. шк., 2003. – 268 с.
7 Мирошник И. В. Теория автоматического управления. Линей-
ные системы. – СПб. : Питер, 2005. – 336 c.
8 Горошков Б. И. Автоматическое управление. – М. : ИРПО: Из-
дательский центр «Академия», 2003. – 304 с.
9 Воронов А. А. Основы теории автоматического управления. –
М. - Л. : Энергия, 1965. – 321 с.
10 Иванов А. А. Теория автоматического управления и регули-
рования. – М. : Недра, 1970. – 224 с.
11 Воронов А. А. Основы теории автоматического управления.
Автоматическое регулирование непрерывных линейных систем. – М. :
Энергия, 1980. – 337 с.
12 Егоров К. В. Основы теории автоматического регулирования.
– М. : Энергия, 1967. – 648 с.
13 Гальперин М. В. Автоматическое управление. – М. : Форум:
ИНФРА-М, 2004. – 224 с.
14 Ерофеев А. А. Теория автоматического управления. – СПб. :
Политехника, 2005. – 302 с.
15 Лукас В. А. Теория автоматического управления. – М. : Не-
дра, 1990. – 416 с.
16 Теория автоматического управления. Ч. 1. – Под ред. проф.
А. В. Нетушила. – М. : Высшая школа, 1968. – 421 с.

309
Приложение А
(справочное)
Таблица соответствия оригиналов и изображений
Таблица А.1
Изображение X(s) Оригинал x(t)
ke
–τs
k∙1(t–τ) запаздывание на τ > 0
1
k
импульсная функция k∙δ(t)
k s
– простой нулевой корень скачок k∙1(t) или просто k
1n
s
n
k
!
– кратный
нулевой корень
k∙t
n
– степенной ряд от t
s
1
k
– простой
действительный корень
t
e
k
– экспонента
n
s
k
)(
– кратный
действительный корень
1
( 1)!
n
t
k e
n
t
, при n > 1
2 2
k
s
– сопряженные
мнимые корни
k∙sinβt – гармоническая
функция
2 2
ks
s
– сопряженные
мнимые корни
k∙cosβt – гармоническая
функция
2 2
( )s
sin
t
e t
- затухающая
гармоническая функция
2 2
( )
s
s
cos
t
e t
- затухающая
гармоническая функция
сопряженные комплексные корни
j
, объединенные в одну дробь
22
s
DCs
)(
,
с вычислением
CD
E
а) предпочтительная форма
tEtCe
t
sincos
б) через синус (угол в радианах)
E
C
arctgtECe
22t
sin
в) через косинус (угол в радианах)
C
E
arctgtECe
22t
cos
сопряженные комплексные корни
(раздельное представление)
js
jdc
js
jdc
tdtce2
t
sincos
перед d ставят плюс, если знаки
мнимых частей изображения в чис-
лителе и знаменателе совпадают (как
показано), а иначе минус
Примечание – Даже если скачок 1(t) в формуле для входной функции не пишет-
ся, то всегда подразумевается, т.к. по Лапласу при t = 0
-
любая функция f(t) равна нулю, а
затем она появляется скачком. Однако сомножитель 1/s вводят в изображение входной
функции лишь в том случае, если она представляет собой чисто ступенчатое воздействие,
даже если в функциях-оригиналах другого вида скачок и был указан.

310
Приложение Б
(справочное)
Расчет числителей простых дробей
Метод неопределенных коэффициентов (системы уравнений).
Универсальный, хотя и громоздкий, метод, пригодный для любых
корней характеристического полинома.
Левую и правую часть разложения на простые дроби приводят к
общему знаменателю, который отбрасывается. Приравнивая коэффи-
циенты при одинаковых степенях s левой и правой частей равенства,
составляют систему линейных алгебраических уравнений и решают ее
любым известным методом.
Пример. Изображение )/()( ss1sY
2
разлагается на две дроби
1s
k
s
k
1ss
1
10
)(
в соответствии с полюсами s
1
= 0; s
2
= -1. Приводим левую и правую
части к общему знаменателю, отбрасывая его, группируем коэффици-
енты, приравниваем коэффициенты при одинаковых степенях s слева
и справа
1=k
0
s +k
0
+ k
1
s = (k
0
+ k
1
)s + k
0
при s
0
→
при s
1
→
10
0
kk0
k1
откуда
k
0
= 1
k
1
= -1
Подставляем значения коэффициентов числителей
1
s
1
s
1
sY
)(
и переходим по таблице соответствия от изображений к оригиналам
t
e1ty
)( .
Метод подстановки полюсов (пригоден только для простых
полюсов или дроби с полюсом максимальной кратности).
Формула:
ps
p
sYpsk
)()(
Пример: возьмем ту же функцию
1s
k
s
k
1ss
1
sY
10
)(
)(
.
