Caballero B. (ed.) Encyclopaedia of Food Science, Food Technology and Nutrition. Ten-Volume Set

Подождите немного. Документ загружается.

0012 During a convective heat transfer process, energy is

theoretically transferred by convection alone. How-

ever, in practice, conduction, radiation, and mass

transfer may also occur at the same time. In blast

cooling/freezing operations, the conductive heat

transfer component is usually very small and can be

neglected. The significance of the radiation heat

transfer and evaporative cooling due to mass transfer

must be considered on an individual basis, and their

effects upon the total heat transfer must be properly

incorporated. Researchers often define an ‘effective’

heat transfer coefficient, which includes the effects of

convection and radiation heat transfer, as well as the

energy transfer due to evaporation of moisture from

the surface of the food item.

Thermal Properties of Foods

0013 The thermal properties of foods are important in the

design of food storage and refrigeration equipment as

well as in the estimation of process times for refriger-

ating, freezing, heating, or drying of foods. Because

the thermal properties of foods are strongly depend-

ent upon chemical composition and temperature, the

most viable option is to predict these thermal proper-

ties using mathematical models that account for the

effects of chemical composition and temperature.

0014Composition data for foods are readily available in

the literature. These data consist of the mass fractions

of the major food components: water, protein, fat,

carbohydrate, fiber, and ash. Food thermal properties

can be predicted by using these composition data in

conjunction with temperature-dependent mathemat-

ical models of the thermal properties of the individual

food components.

0015Equations for predicting the thermal properties of

these food components have been developed as func-

tions of temperature in the range of 40 to 150



These equations are presented in Table 1. Because

water is the predominant constituent in most food

items, the water content of food items significantly

influences the thermophysical properties of foods.

Therefore, equations for predicting the thermal prop-

erties of water and ice have also been developed.

These equations are presented in Table 2.

0016In general, the thermophysical properties of a food

item are well behaved when the temperature of the

food item is above its initial freezing point. However,

tbl0001 Table 1 Thermal property equations for food components (40



C t  150



Thermalproperty Food component Thermalproperty model

Thermal conductivity (W m

1

) Protein k ¼1.7881 10

1

þ1.1958 10

3

t 2.7178 10

6

Fat k ¼1.8071 10

1

2.7604 10

3

t 1.7749 10

7

Carbohydrate k ¼2.0141 10

1

þ1.3874 10

3

t 4.3312 10

6

Fiber k ¼1.8331 10

1

þ1.2497 10

3

t 3.1683 10

6

Ash k ¼3.2962 10

1

þ1.4011 10

3

t 2.9069 10

6

Density (kg m

3

) Protein r ¼1.3299 10

5.1840 10

1

Fat r ¼9.2559 10

4.1757 10

1

Carbohydrate r ¼1.5991 10

3.1046 10

1

Fiber r ¼1.3115 10

3.6589 10

1

Ash r ¼2.4238 10

2.8063 10

1

Specific heat (J kg

1

) Protein c

¼2.0082 10

þ1.2089t 1.3129 10

3

Fat c

¼1.9842 10

þ1.4733t 4.8008 10

3

Carbohydrate c

¼1.5488 10

þ1.9625t 5.9399 10

3

Fiber c

¼1.8459 10

þ1.8306t 4.6509 10

3

Ash c

¼1.0926  10

þ1.8896t 3.6817 10

3

tbl0002 Table 2 Thermal property equations for water and ice (40



C  t  150



Thermal property Thermalproperty model

Water Thermal conductivity (W m

1

) k

¼5.7109 10

1

þ1.7625 10

3

t 6.7036 10

6

Density (kg m

3

) r

¼9.9718 10

þ3.1439 10

3

t  3.7574 10

3

Specific heat (J kg

1

)

¼4.0817 10

5.3062t þ9.9516 10

1

Specific heat (J kg

1

)

¼4.1762 10

9.0864 10

2

t þ5.4731 10

3

Ice Thermal conductivity (W m

1

) k

ice

¼2.2196 6.2489 10

3

t þ1.0154 10

4

Density (kg m

3

) r

ice

¼9.1689 10

1.3071 10

1

Specific heat (J kg

1

) c

ice

¼2.0623 10

þ6.0769t

For the temperature range of 40 to 0



For the temperature range of 0 to 150



2708 FREEZING/Principles

below the initial freezing point, the thermophysical

properties of a food item vary dramatically with

temperature.

Specific Heat Capacity

0017 Specific heat capacity is a measure of the energy

transfer required to effect a temperature change and

can be used to calculate the heat load imposed on the

refrigeration equipment by the freezing of foods. In

unfrozen foods, specific heat capacity is relatively

constant with respect to temperature. However, for

frozen foods, there is a large decrease in specific heat

capacity as the temperature decreases.

Unfrozen

0018 The specific heat capacity of an unfrozen food item,

, can be obtained from the mass average of the

specific heat capacities of its components:

, ð6 Þ

where the c

denotes the specific heat capacities of the

individual food components, and w

denotes their

mass fractions.

0019 If detailed composition data are not available, a

simpler equation for the specific heat capacity of an

unfrozen food item can be used:

¼ 4190  2300w

 628w

, ð7 Þ

where c

is the specific heat capacity of the unfrozen

food item (J kg

1

), and w

is the mass fraction of

the solids in the food item.

Frozen

0020 Below the initial freezing point of the food item, the

sensible energy due to temperature change and

the latent energy due to the fusion of water must be

considered. Because latent heat is not released at a

constant temperature, but rather over a range of tem-

peratures, an apparent specific heat capacity can be

used to account for both the sensible and latent heat

effects. To develop expressions for apparent specific

heat capacity, first consider the specific enthalpy of a

frozen food. The specific enthalpies of the food con-

stituents are additive. Further, assume that the food is

composed of solids, liquid water, and ice. Then, the

specific enthalpy of the frozen food, h, can be mod-

eled as:

h ¼ h

þ h

ice

, ð8 Þ

where h

is the specific enthalpy of the solid constitu-

ents, h

is the specific enthalpy of water, and h

ice

the specific enthalpy of ice. Differentiating eqn (8)

with respect to temperature at constant pressure

yields an expression for the apparent specific heat

capacity, c

¼ c

þ c

ice

þ h

ice

ð9Þ

where c

is the specific heat capacity of the solid

constituents, c

is the specific heat capacity of

water, and c

ice

is the specific heat capacity of ice.

0021Assuming that high moisture content food items

can be modeled as ideal dilute solutions, and noting

that qw

/qT ¼qw

ice

/ qT, the following equation for

the apparent specific heat capacity of high moisture

content food items can be derived:

¼ c

þ w

 w

ðÞc þ Ew

 0:8c



, ð10Þ

where Dc is the difference between the specific heat

capacities of water and ice ( Dc ¼ c

 c

ice

), E is the

ratio of the molar masses of water, M

, and food

solids, M

,(E ¼ M

), R is the ideal gas constant,

is the freezing point of water (T

¼ 273.2 K), and

t is the food temperature (



C).

0022A slightly simpler apparent specific heat capacity

equation, which is similar in form to that of eqn (10),

is given as follows:

¼ 1550 þ 1260w

:ð11Þ

Specific Enthalpy

0023The change in specific enthalpy of a food item can be

used to estimate the energy that must be removed

from a food item in order to effect a temperature

change. Above the freezing point, specific enthalpy

consists of sensible energy, whereas below the initial

freezing point, specific enthalpy consists of both sens-

ible and latent energy.

0024Specific enthalpy may be obtained from the defin-

ition of the constant pressure specific heat capacity:



, ð12Þ

where c

is the constant pressure specific heat cap-

acity, h is the specific enthalpy, and T is temperature.

Equations for specific enthalpy may be obtained by

integrating expressions of specific heat capacity with

respect to temperature.

Unfrozen

0025The specific enthalpy of an unfrozen food item, h,

may be determined by integrating eqn (6) as follows:

FREEZING/Principles 2709

h ¼

dT, ð13Þ

where h

is the specific enthalpy of the individual

food components, and w

is the mass fraction of

the food components.

002 6 Integration of eqn (7) from the initial freezing point

of a food item, t

, to a temperature, t, above the

freezing point would yield:

h ¼ðt  t

Þð4190  2300w

 628w

Þ:ð14Þ

This equation, however, would predict zero specific

enthalpy at the initial freezing point of the food item,

. Typically, in the literature for food refrigeration,

the reference temperature for zero specific enthalpy is

 40



C. Thus, in order to make eqn (14) consistent

with zero specific enthalpy at  40



C, an additional

term must be added to eqn (14), namely, the specific

enthalpy at the initial freezing point, h

h ¼ h

þðt  t

Þð4190  2300w

 628w

Þ:ð15Þ

The specific enthalpy at the initial freezing point, h

may be estimated by evaluating eqn (17) at the initial

freezing temperature of the food, as discussed below.

Frozen

002 7 Integration of eqn (10) between a reference tempera-

ture, T

, and the food temperature, T, leads to the

following expression for the specific enthalpy of a

frozen food:

h ¼ðT  T

Þ c

þðw

 w

Þc



þ Ew

ðT

 T

ÞðT

 T Þ

 0 :8 c



ð16Þ

Generally, the reference temperature, T

, is taken to

be 233.2 K (  40



C) at which point the enthalpy is

defined to be zero.

002 8 By integrating eqn (11) between a reference

temperature, T

, and the food temperature, T, the

following expression for specific enthalpy below

the initial freezing point may be obtained:

h ¼ðt  t

Þ 1500 þ 1260w

, þ



:ð17Þ

Thermal Conductivity

002 9 Thermal conductivity is the material property that

relates the conduction heat transfer rate to the tem-

perature gradient. The thermal conductivity of a food

item depends upon many factors, including the com-

position, structure, and temperature of the food item.

0030Early work in the modeling of food thermal con-

ductivity includes an adaption of Maxwell’s equation.

This model is based upon the thermal conductivity of

dilute dispersions of small spheres in a continuous

phase:

k ¼ k

1 ½1  aðk

Þb

1 þða  1Þb

, ð18Þ

where k is the conductivity of the mixture, k

is the

conductivity of the continuous phase, k

is the con-

ductivity of the dispersed phase, a ¼ 3k

/(2k

þ k

b ¼ V

/(V

þ V

), V

is the volume of the dispersed

phase, and V

is the volume of the continuous phase.

0031In an effort to account for the different structural

features of foods, thermal conductivity models for

both homogeneous and fibrous food items have

been developed. The differences in thermal conduct-

ivity parallel and perpendicular to the food fibers are

taken into account in these fibrous food thermal

conductivity models.

0032For an isotropic, homogeneous two-component

system composed of continuous and discontinuous

phases, in which the thermal conductivity is inde-

pendent of the direction of heat flow, the following

expression may be used to determine thermal con-

ductivity, k:

k ¼ k

1  L

ð1  LÞ



, ð19Þ

where k

is the thermal conductivity of the continuous

phase, and L

is the volume fraction of the discon-

tinuous phase. In eqn (19), it is assumed that the

thermal conductivity of the continuous phase is

much larger than the thermal conductivity of

the discontinuous phase.

0033For an anisotropic, fibrous two-component system

in which the thermal conductivity is dependent upon

the direction of heat flow, two expressions for ther-

mal conductivity have been developed. For heat flow

that is parallel to the food fibers, the following

expression may be used to determine thermal con-

ductivity, k

¼ k

1  N

1 



, ð20Þ

where N

is the volume fraction of the discontinuous

phase in the fibrous food product. If the heat flow

is perpendicular to the food fibers, the following

expression for thermal conductivity, k

, applies:

¼ k

1  P

1  Pð1  NÞ



, ð21Þ

where P ¼ N(1  k

2710 FREEZING/Principles

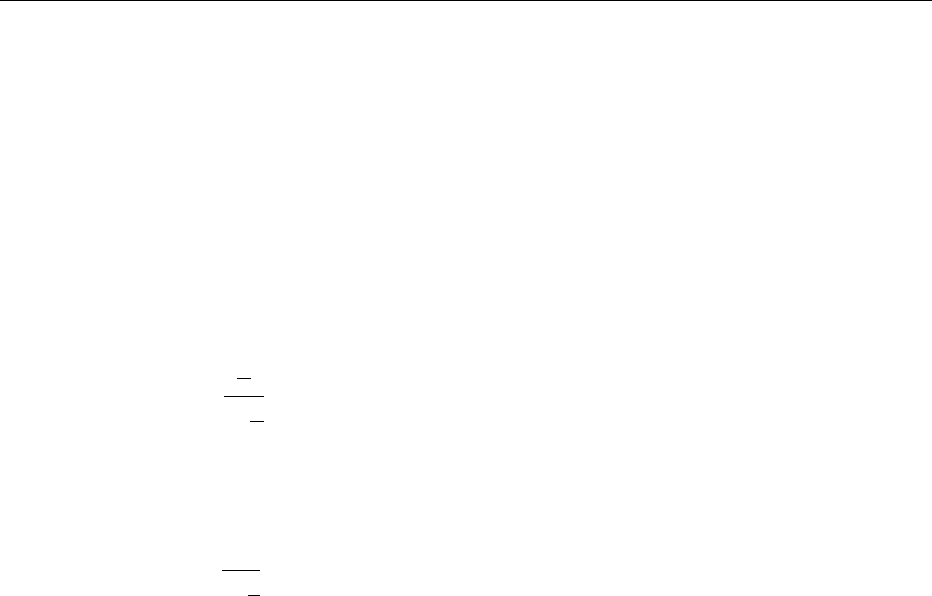
0034 For multicomponent systems, numerous research-

ers have proposed the use of parallel and perpendicu-

lar (or series) thermal conductivity models based

upon analogies with electrical resistance. The parallel

model is simply the sum of the thermal conductivities

of the food constituents multiplied by their volume

fractions:

k ¼

i¼1



, ð 22Þ

where f

is the volume fraction of constituent i. The

volume fraction of constituent i can be found from

the following equation:





j¼1



: ð23Þ

The perpendicular model is the reciprocal of the

sum of the volume fractions divided by their thermal

conductivities:

k ¼

i¼1



: ð24Þ

These two models have been found to predict the

upper and lower bounds of the thermal conductivity

of most food items.

Further Readings

Becker BR and Fricke BA (1999) Evaluation of semi-analyt-

ical/empirical freezing time estimation methods, Part I:

Regularly shaped food items. International Journal of

Heating, Ventilating, Air-Conditioning, and Refrigerat-

ing Research 5: 151–169.

Becker BR and Fricke BA (1999) Evaluation of semi-analyt-

ical/empirical freezing time estimation methods, Part II:

Irregularly shaped food items. International Journal of

Heating, Ventilating, Air-Conditioning, and Refrigerat-

ing Research 5: 171–187.

Becker BR and Fricke BA (1999) Freezing times of regularly

shaped food items. International Communications in

Heat and Mass Transfer 26: 617–626.

Becker BR and Fricke BA (1999) Food thermophysical

property models. International Communications in

Heat and Mass Transfer 26: 627–636.

Becker BR, Misra A and Fricke BA (1996) Bulk refriger-

ation of fruits and vegetables, Part I: theoretical consid-

erations of heat and mass transfer. International Journal

of Heating, Ventilating, Air-Conditioning, and Refriger-

ating Research 2: 122–134.

Becker BR, Misra A and Fricke BA (1996) Bulk refriger-

ation of fruits and vegetables, Part II: Computer algo-

rithm for heat loads and moisture loss. International

Journal of Heating, Ventilating, Air-Conditioning, and

Refrigerating Research 2: 215–230.

Chen CS (1985) Thermodynamic analysis of the freezing

and thawing of foods: Enthalpy and apparent specific

heat. Journal of Food Science 50: 1158–1162.

Choi Y and Okos MR (1986) Effects of temperature and

composition on the thermal properties of foods. In:

LeMaguer M and Jelen P (eds) Food Engineering and

Process Applications, vol. 1, pp. 93–101. London:

Elsevier Applied Science.

Eucken A (1940) Allgemeine Gesetzmassigkeiten fur das

Warmeleitvermogen verschiedener Stoffarten und Agg-

regatzustande. Forschung auf dem Gebiete des Inge-

nieurwesens, Ausgabe A 11: 6.

Franks F (1982) The properties of aqueous solutions at

subzero temperatures. In: Water: A Comprehensive

Treatise, vol. 7, pp. 215–338. New York: Plenum.

Franks F, Asquith MH, Hammond CC, Skaer H leB and

Echlin P (1977) Polymeric cryoprotectants in the preser-

vation of biological ultrastruture, I: Low temperature

states of aqueous solutions of hydrophilic polymers.

Journal of Microscopy 110: 223–238.

Fricke BA and Becker BR (2001) Evaluation of thermophy-

sical property models for foods. International Journal of

Heating, Ventilating, Air-Conditioning and Refrigerat-

ing Research 7: 311–330.

Holland B, Welch AA, Unwin ID et al. (1991) McCance and

Widdowson’s – The Composition of Foods. Cambridge,

UK: Royal Society of Chemistry and Ministry of Agri-

culture, Fisheries and Food.

Kopelman I (1966) Transient Heat Transfer and Thermal

Properties in Food Systems. PhD thesis. Michigan State

University. East Lansing, MI.

MacKenzie AP (1977) Freezing behaviour of aqueous solu-

tions. Philosophical Transactions of the Royal Society of

London B 278: 167–189.

Murakami EG and Okos MR (1989) Measurement and

prediction of thermal properties of foods. In: Singh

RP and Medina AG (eds) Food Properties and

Computer-aided Engineering of Food Processing

Systems pp. 3–48. Dordrecht: Kluwer Academic.

Schwartzberg HG (1976) Effective heat capacities for the

freezing and thawing of food. Journal of Food Science

41: 152–156.

Slade L and Levine H (1988) Non-equilibrium behavior of

small carbohydrate–water systems. Pure and Applied

Chemistry 60: 1841–1864.

Tchigeov G (1979) Thermophysical Processes in Food

Refrigeration Technology. Moscow: Food Industry.

USDA (1996) Nutrient Database for Standard Reference,

Release 11. Washington, DC: US Department of

Agriculture.

FREEZING/Principles 2711

Operations

B R Becker and B A Fricke, University of Missouri-

Kansas City, Kansas City, MO, USA

Introduction

0001 Freezing operations can be grouped by their basic

method of extracting heat from foods. Blast freezing

utilizes convection heat transfer to remove heat from

foods while contact freezing makes use of conduction

heat transfer to remove energy from foods. Cryogenic

freezing may utilize convection and/or conduction

heat transfer to remove heat from foods.

Blast Freezers

0002 Blast freezers use air as the heat transfer medium and

depend on contact between the product and the air.

Sophistication in air flow control and conveying tech-

niques varies from crude blast freezing chambers to

carefully controlled impingement-style freezers. (See

Freezing: Blast and Plate Freezing.)

Blast-Cell Freezer

0003 The blast-cell freezer, shown in Figure 1, is the sim-

plest design and consists of an insulated enclosure

equipped with refrigeration coils and fans that circu-

late the air over the food items in a controlled way.

Products are placed on trays, which are then placed

into racks in such a way that an air space is left be-

tween adjacent layers of trays. The racks are moved in

and out of the tunnel manually. Almost all products

may be frozen either individually or in cartons in a

blast-cell freezer. Because labor requirements are rela-

tively high and product flow is cumbersome, blast-

cell freezers are suitable for small quantities of varied

products.

Straight-Belt Freezer

0004The straight-belt freezer, shown in Figure 2, utilizes a

wire mesh belt conveyor in a blast room, which pro-

vides continuous product flow. Vertical air flow is

used, which forces cold air up through the product

layer, thereby creating good contact between the air

and the product. Straight-belt freezers are generally

used with fruits, vegetables, French fried potatoes,

cooked meat toppings (e.g., diced chicken), and

cooked shrimp.

0005Straight-belt freezers usually incorporate a two-

stage belt composed of two mesh conveyor belts in

series. The first stage initially precools or crust-freezes

the outer layer of the product before it is transferred

to the second stage for final freezing and sensible

cooling to 18



C or below. Freezing times range

from 3 to 50 min.

0006For products with longer freezing times or higher

capacity requirements, the freezer footprint can be

reduced by stacking belts above each other to form

a multipass system, as shown in Figure 3. However,

this type of freezing system has the potential for prod-

uct damage and jams at the belt transfers.

fig0001 Figure 1 Blast-cell freezer (Ingvar).

fig0003Figure 3 Multipass belt freezer (Advanced Equipment, Inc.).

fig0002Figure 2 Straight-belt freezer (Advanced Equipment, Inc.).

2712 FREEZING/Operations

Spiral-Belt Freezer

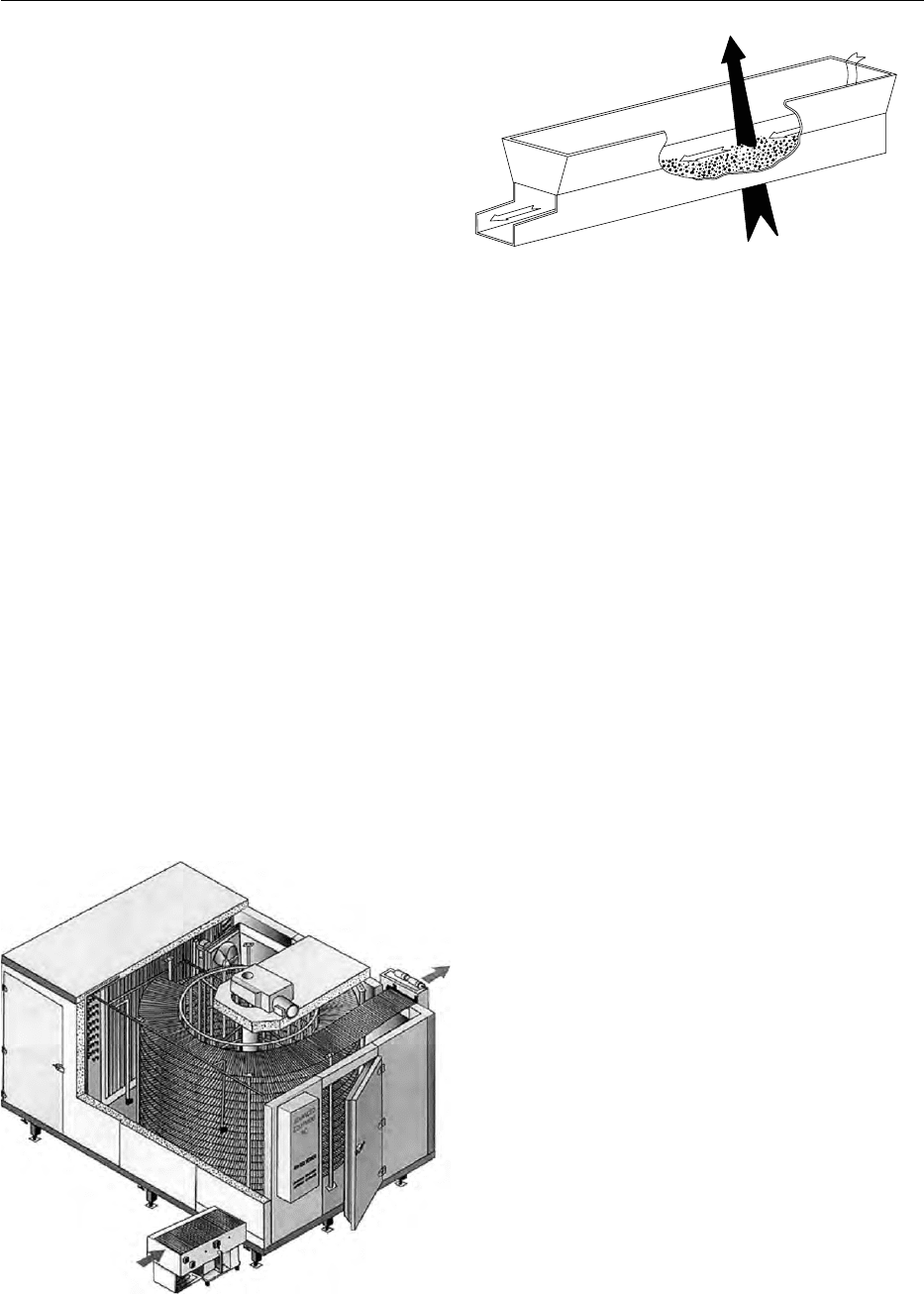
0007 The spiral-belt freezer, shown in Figure 4, is often

used for products that require gentle handling or a

long freezing time (generally 10 min to 3 h). This

freezer consists of an endless conveyor belt that is

wrapped cylindrically, one tier above or below the

last, to form a configuration which requires minimal

floor space for a relatively long belt. The number of

tiers in the spiral can be varied to accommodate dif-

ferent capacities and two or more spiral towers can be

used in series for products with long freezing times.

Modular and field-erected spiral freezers are avail-

able in a range of belt widths and lengths to accom-

modate various upstream processes and capacity

requirements.

0008 In spiral freezers, horizontal air flow is usually

supplied by axial fans mounted along one side of the

spiral which blow air horizontally across the spiral

conveyor. Some freezers incorporate more sophisti-

cated air flow control utilizing extensive baffling

and high-pressure fans.

0009 Typical products frozen in spiral-belt freezers in-

clude raw and cooked meat patties, fish fillets, chicken

portions, pizza, and a variety of packaged products.

Fluidized-Bed Freezers

0010 The fluidized-bed freezer, shown in Figure 5, utilizes

air for product transport and heat transfer. The high

degree of fluidization improves the heat transfer rate

and is well suited for small, uniform-sized particulate

products such as peas, resulting in a freezing time of

3–11 min.

Fluidized-Belt Freezers

0011The fluidized-belt freezer is a hybrid of the belt and

fluidized-bed freezers which incorporates a fluidizing

section in the first belt stage. It is designed to provide

fluidizing conditions for wet incoming product with a

belt to assist the transport of heavier products that do

not fluidize fully. Once crust-frozen, the product can

be loaded deeper for greater efficiency on the second

belt.

Contact Freezers

0012Contact freezers utilize conduction heat transfer

whereby the product or package is placed in direct

contact with a refrigerated surface. (See Freezing:

Blast and Plate Freezing.)

Plate Freezers

0013The most common type of contact freezer is the plate

freezer, in which the product is pressed between metal

plates, as shown in Figure 6. Refrigerant is circulated

inside channels in the plates, insuring efficient heat

transfer and short freezing times. Plate freezers are

especially suited for products that are good conduct-

ors of heat, such as fish fillets, chopped spinach, or

meat offal. The plate freezer’s heat transfer advantage

is reduced with increasing product thickness, which is

often limited to 5–8 cm.

0014For packaged products, an additional advantage of

plate freezers is that pressure from the plates minim-

izes any bulging that may occur during freezing,

resulting in packages that are even and square. How-

ever, packages or cavities should be well filled to

insure efficient freezing.

0015Contact plate freezers are available in horizontal or

vertical arrangements with manual loading and

unloading. Horizontal plate freezers are also avail-

able with automatic loading and unloading, resulting

in higher capacities and continuous operation. Auto-

matic plate freezers can accommodate up to 200

packages per minute, with freezing times from 10 to

150 min.

Product flow

Air flow

fig0005Figure 5 Fluidized-bed freezer (ASHRAE).

fig0004 Figure 4 Spiral-belt freezer (Advanced Equipment, Inc.).

FREEZING/Operations 2713

Specialized Contact Freezers

001 6 A combination of air and contact freezing is often

used for wet fish fillets and similar soft, wet products

with relatively large, flat surfaces. The product is

placed on to a continuous, solid stainless-steel belt

and freezing is usually accomplished both by conduc-

tion through the belt to a cooling medium below the

belt and by convection through controlled air flow

above the belt. Another specialized contact freezer

conveys food products on a continuous plastic film

over a low-temperature refrigerated plate, thus elim-

inating product deformation or wire mesh belt mark-

ings on products which are flat, wet, and sticky, soft,

or in need of hand-shaping before freezing. These

freezer designs produce attractive product, but a

drawback is the physical size of the freezer. Freezing

times of less than 30min can be achieved with these

types of freezer.

Cryogenic Freezers

001 7 Cryogenic freezers use liquid nitrogen or liquid

carbon dioxide as the refrigeration medium, and the

freezers may be batch cabinets, straight-belt freezers,

spiral conveyors, or liquid immersion freezers. While

cryogenic freezers represent a low initial investment,

they have a high operating cost. Consequently, cryo-

genic freezing is often utilized for small-scale produc-

tion, new products, overload situations, or seasonal

products.

0018The most common type of cryogenic freezer is a

straight-through, single-belt tunnel. Liquid nitrogen

at 196



C or carbon dioxide at 79



C is introduced

at the outfeed end of the freezer, directly on to the

product. As the liquid nitrogen or carbon dioxide

vaporizes, the cold vapors are circulated toward the

infeed end, where they are used for precooling and

initial freezing of the product. The warmed vapors

(typically 45



C) are then discharged to the atmos-

phere. The low temperature of the liquid and vapor-

ous nitrogen or carbon dioxide provides rapid

freezing, which can improve quality and reduce dehy-

dration for some products. However, the freezing cost

ishigh,andthesurfaceofproductshavingahighwater

content may crack if precautions are not taken. (See

Freezing: Cryogenic Freezing.)

Freezing Time Estimation Methods

0019In order for food freezing operations to be cost-

effective, it is necessary to design the refrigeration

equipment optimally to fit the specific requirements

of the particular freezing application. This requires

estimation of the freezing times of foods, as well as

the corresponding refrigeration loads.

0020Theoretically, the freezing of foods can be de-

scribed via the Fourier heat conduction equation:

c





ð1Þ

where T is temperature, t is time, r is the density of

the food, c is the specific heat of the food, k is the

thermal conductivity of the food, and x, y, and z are

the coordinate directions. For ideal, regularly shaped

food items with constant thermophysical properties,

uniform initial conditions, constant external condi-

tions, and a prescribed surface temperature or a

convection boundary condition, exact analytical so-

lutions for eqn (1) exist which allow for the estima-

tion of the freezing times of foods. However, for

realistic freezing processes, the food items are gener-

ally irregularly shaped with temperature-dependent

thermophysical properties and therefore it is not pos-

sible to derive exact analytical solutions for the freez-

ing times of foods.

0021As a result of this difficulty, most of the research

effort has been in the development of semianalytical/

fig0006 Figure 6 Plate freezer (Ingvar).

2714 FREEZING/Operations

empirical food freezing time prediction methods

which make use of various simplifying assumptions.

Numerous such methods have been proposed, and the

designer is thus faced with the challenge of selecting

an appropriate estimation method from the plethora

of available methods.

0022 In the following section, the basic freezing time

estimation method developed by Plank is discussed

first, followed by a discussion of those methods which

are based upon modifications of Plank’s equation.

The discussion then focuses on those freezing time

estimation methods in which the freezing time is cal-

culated as the sum of the precooling, phase change,

and subcooling times. The last section deals with

freezing time estimation methods which account for

irregularly shaped food items.

Plank’s Equation

0023 The most widely known method for estimating the

freezing times of foods was developed by R. Plank in

1913. In this method, it is assumed that only convect-

ive heat transfer occurs between the food item and the

surrounding cooling medium. In addition, it is as-

sumed that the food item is at its initial freezing

temperature and that this temperature is constant

throughout the freezing process. Furthermore, a con-

stant thermal conductivity for the frozen region is

assumed. Plank’s freezing time estimation method is

given as follows:

t ¼

 T



ð2Þ

where L

is the volumetric latent heat of fusion, T

the initial freezing temperature of the food, T

is the

freezing medium temperature, D is the thickness of

the slab or the diameter of the sphere or infinite

cylinder, h is the convective heat transfer coefficient,

is the thermal conductivity of the fully frozen

food, and P and R are geometric factors. For the

infinite slab, P ¼

and R ¼

. For a sphere, P and R

are

and

, respectively, and for an infinite cylinder,

P ¼

and R ¼

0024 The geometric factors, P and R, provide insight as

to the effect of shape upon freezing time. Plank’s

shape factors indicate that an infinite slab of thickness

D, an infinite cylinder of diameter D and a sphere of

diameter D, if exposed to the same conditions, would

have freezing times in the ratio of 6:3:2. Hence, a

cylinder will freeze in half the time of a slab and a

sphere will freeze in one-third the time of a slab.

0025 Various researchers have noted that Plank’s

method does not accurately predict the freezing

times of foods because it assumes that freezing of

foods takes place at a constant temperature, and not

over a range of temperatures, as is the case in actual

food freezing processes. In addition, the thermal con-

ductivity of the frozen food is assumed to be constant,

but in reality, the thermal conductivity varies greatly

during freezing. Another limitation of Plank’s equa-

tion is that it neglects the removal of sensible heat

above the freezing point. Furthermore, Plank’s

method is only applicable to infinite slabs, infinite

cylinders, and spheres. Researchers have subse-

quently focused upon development of improved

freezing time estimation methods which account for

precooling and subcooling times, nonconstant ther-

mal properties, irregular geometries, and phase

change over a range of temperatures.

Modifications to Plank’s Equation

0026Modifications to Plank’s equation include corrections

to account for the removal of sensible heat both

above and below the initial freezing point of

the food as well as temperature variation during

freezing. Regression equations were developed to

estimate the geometric parameters, P and R, for infin-

ite slabs, infinite cylinders, and spheres. In these

regression equations, the effects of surface heat

transfer, precooling, and final subcooling are ac-

counted for by means of the Biot number, Bi, the

Plank number, Pk, and the Stefan number, Ste,

respectively.

0027The Biot number, Bi, is defined as follows:

Bi ¼

ð3Þ

In the literature for freezing of foods, it is accepted

that the characteristic dimension, D, is defined as

twice the shortest distance from the thermal center

of a food item to its surface. For an infinite slab, D is

the thickness. For an infinite cylinder or a sphere, D

is the diameter. These definitions will be adopted for

this article, unless otherwise noted.

0028In general, the Plank number, Pk, is defined as

follows:

Pk ¼

ðT

 T

H

ð4Þ

where C

is the volumetric specific heat of the un-

frozen phase and DH is the volumetric enthalpy

change of the food between T

and the final food

temperature. The Stefan number, Ste, is similarly de-

fined as follows:

Ste ¼

ðT

 T

H

ð5Þ

where C

is the volumetric specific heat of the frozen

phase.

FREEZING/Operations 2715

0029 The freezing times of foods are then calculated with

a modified version of Plank’s equation. Plank’sori-

ginal geometric factors, P and R, are replaced with

the modified values given in Table 1, and the latent

heat, L

, in Plank’s equation is replaced with the

volumetric enthalpy change of the food, DH

, be-

tween the freezing temperature, T

, and the final

center temperature, assumed to be 10



C. As

shown in Table 1, the geometric factors P and R are

functions of the Plank number, Pk, and the Stefan

number, Ste. Both of these parameters should be

evaluated using the enthalpy change DH

. Thus,

the modified Plank equation takes the following

form:

t ¼

H

 T



ð6Þ

Precooling, Phase Change, and Subcooling Time

Calculations

0030 Numerous researchers have taken a different ap-

proach to account for the effects of sensible heat

removal above and below the initial freezing point.

In these methods, the total freezing time, t, is the sum

of the precooling, phase change, and subcooling

times:

t ¼ t

þ t

ð7Þ

where t

, t

, and t

are the precooling, phase change,

and subcooling times, respectively.

0031 An example of a freezing time estimation method

in which sensible heat effects are included by calcu-

lating precooling, phase change, and subcooling times

separately is given below. The use of a mean freezing

point, which is assumed to be 1.5 K below the initial

freezing point of the food, accounts for freezing

which takes place over a range of temperatures. The

freezing time estimation method is stated in terms of

the volume and surface area of the food item and is

therefore applicable to food items of any shape. This

method is given as:

T

1 þ



; i ¼ 1; 2; 3 ð8Þ

with the variables defined as shown in Table 2.

Geometric Considerations

0032Equivalent heat transfer dimensionality A geomet-

ric correction factor, called the equivalent heat trans-

fer dimensionality, E, was introduced to calculate the

freezing times of irregularly shaped food items. In this

method, the freezing time of an irregularly shaped

object, t

shape

, is related to the freezing time of an

infinite slab, t

slab

, via the equivalent heat transfer

dimensionality, E, as follows:

shape

slab

ð9Þ

The freezing time of the infinite slab is then calculated

from one of the many suitable freezing time estima-

tion methods available for infinite slabs.

0033Expressions for determining the equivalent heat

transfer dimensionality of infinite slabs, infinite and

finite cylinders, rectangular bricks, spheres, and two-

and three-dimensional irregular shapes are given as

follows:

E ¼ G

þ G

ð10Þ

where:

¼ Xð2:32=

1:77



þ½1  Xð2:32=

1:77

Þ

0:73



2:50

ð11Þ

¼ Xð2:32=

1:77



þ½1  Xð2:32=

1:77

Þ

0:73



2:50

ð12Þ

tbl0001 Table 1 Expressions for P and R

Shape P and R expressions

Infinite slab

P ¼ 0:5072 þ 0:2018Pk þ Ste 0:3224Pk þ

0:0105

þ 0:0681



R ¼ 0:1684 þ Steð0:2740Pk  0:0135Þ{

Infinite cylinder P ¼ 0:3751 þ 0:0999Pk þ Ste 0:4008Pk þ

0:0710

 0:5865



R ¼ 0:0133 þ Steð0:0415Pk þ 0:3957Þ{

Sphere P ¼ 0:1084 þ 0:0924Pk þ Ste 0:231Pk 

0:3114

þ 0:6739



R ¼ 0:0784 þ Steð0:0386Pk  0:1694Þ{

2716 FREEZING/Operations

XðxÞ¼x =ðBi

1:34

þ xÞð13 Þ

and the geometric constants, G

, G

and G

, are

given in Table 3. The dimensional ratios, b

and b

are defined as follows:



second shortest dimension of the food item

shortest dimension of the food item

ð14 Þ



longest dimension of the food item

shortest dimension of the food item

ð15 Þ

0034 Mean conducting path Knowledge of the Biot

number of a food item is required to utilize freezing

time estimation methods. To calculate the Biot

number of a food item, its characteristic dimension

must be known. Because it is difficult to determine the

characteristic dimension of an irregularly shaped

food item, the concept of the mean conducting path

was introduced. The mean conducting path, D

/2, is

the mean heat transfer length from the surface of the

food item to its thermal center. This mean conducting

path is used to calculate the Biot number which, in

turn, is used in the calculation of the freezing time.

Thus, the Biot number becomes:

Bi ¼

ð16Þ

where D

is twice the mean conducting path.

0035For rectangular blocks of food, the mean conduct-

ing path is proportional to the geometric mean of the

block’s two shorter dimensions. Based upon this

result, an equation to calculate the Biot number, Bi,

for rectangular blocks of food is given as follows:

¼ 1 þ 1 :5

ﬃﬃﬃﬃﬃ



 1

4





(

1 þ



4

)

0:25

ð17Þ

where Bi

is the Biot number based on the shortest

dimension of the block, D

: Bi

¼ hD

/k. The Biot

number, Bi, calculated with eqn (17) is then substi-

tuted into a freezing time estimation method, such as

eqn (8), to calculate the freezing time for rectangular

blocks.

0036It has been noted that for squat-shaped food items,

the mean conducting path, D

/2, could be reasonably

estimated as the arithmetic mean of the longest and

shortest distances from the surface of the food item to

its thermal center.

0037Equivalent sphere diameter The concept of the

equivalent sphere diameter can also be used to calcu-

late the freezing time of irregularly shaped food items.

In this method, a sphere diameter is calculated which

is based upon the volume and the volume-to-surface-

area ratio of the irregularly shaped food item. This

tbl0003Table 3 Geometric constants for equivalent heat transfer

dimensionality

Shape G

Infinite slab 1 0 0

Infinite cylinder 2 0 0

Sphere 3 0 0

Squat cylinder 1 2 0

Short cylinder 2 0 1

Infinite rod 1 1 0

Rectangular brick 1 1 1

Two-dimensional irregular shape 1 1 0

Three-dimensional irregular shape 1 1 1

tbl0002 Table 2 Definition of variables for precooling, phase change,

and subcooling time calculations

Process Variables

Precooling i ¼ 1

¼ 6

¼ C

ðT

 T

ÞV

¼ðBi

þ Bi

Þ=2

T

ðT

 T

ÞðT

 T



Phase change i ¼ 2

¼ 4

¼ L

¼ Bi

T

¼ T

 T

Subcooling i ¼ 3

¼ 6

¼ C

ðT

 T

ÞV

¼ Bi

T

ðT

 T

ÞðT

 T



is the area through which heat is transferred.

is the Biot number for the unfrozen phase.

is the Biot number for the frozen phase.

is the volumetric specific heat for the unfrozen phase.

is the volumetric specific heat for the frozen phase.

is the volumetric latent heat of fusion.

, Q

, and Q

are the heats of precooling, phase change, and subcooling,

respectively.

, DT

, and DT

are the corresponding log-mean temperature driving

forces.

is the final thermal center temperature.

is the initial temperature.

is the mean freezing point, assumed to be 1.5 K below the initial

freezing point.

is the freezing medium temperature.

is the mean final temperature.

V is the volume of the food item.

FREEZING/Operations 2717