Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

4
от точки излома должен быть более высокого порядка, чем справа. Обычная правосторонняя
сплайн-функция в форме (2) аппроксимировать такую зависимость из-за ограничения (4) не
позволяет. Поэтому выбрали левостороннюю сплайн-функцию. Разбиение отрезка х (0,1) на
интервалы производили разным числом узлов - от трех до пяти. Один из этих узлов всегда
соответствовал точке двойной эвтектики (InSb + Sb), остальные (для левой части кривой)
располагали согласно правилам Уолда [3, 6].
При использовании пяти узлов (ψ
0
= 0, ψ
1
=0,27, ψ
3
= 0,49, ψ
4
= 0,703, ψ
5
= 1) строили
кубический левосторонний сплайн
(
)
(
)
j
jji
j
iijji
xxIxy βψψβ
∑
∑
∑
===
+−=
2
010
3
14,3,1
, ; (17)
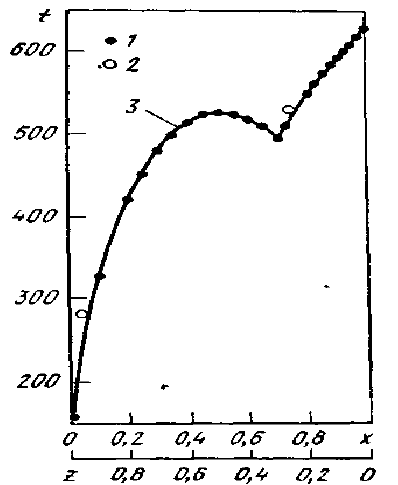
Рис. 2. Кривая ликвидус системы In-Sb:
1 - экспериментальные данные [8]; 2 - выбросы (определены по критерию Смирнова - Груббса [Р2.3] и
исключены); 3 - аппроксимация с помощью сплайн-функций (толщина линии соответствует 95%-му
доверительному интервалу); t - температура (в формулах t = у); х, z - концентрация Sb и In.
при использовании четырех узлов (ψ
0
= 0, ψ
2
= 0,37, ψ
4
= 0,703, ψ
5
= 1) строили сплайн
аналогичной структуры четвертого порядка
(
)
(
)
j
jji
j
iijji
xxIxy βψψβ
∑
∑
∑
===
+−=
2
010
4
14;2
, ; (18)
при использовании трех узлов (ψ
0
= 0, ψ
4
= 0,703, ψ
5
= 1) строили сплайн восьмого порядка
(
)
(
)
j
jj
j
jj
xxIxyβψψβ
∑
∑
==
+−=
2
041044
8
1
, . (19)
Во всех случаях сплайн - аппроксимация кривой справа от точки эвтектики х = 0,703
совпадала с полиномом второго порядка. В выражениях (17) - (19) у – температура,
о
C, х -
концентрация Sb в долях единицы (по массе).
Оценки параметров сплайнов (17) - (19) определяли по обычной программе линейного
регрессионного анализа. Соответствующие сплайны после исключения статистически незначимых
коэффициентов оказались следующими:
у = [1492(х – 0,27)
2
+ 6664(х – 0,27)
3
]⋅I
10
(0,27; х) + 452,1(х - 0,49)
2
⋅I
10
(0,49; x) +
+ [-872,4(х - 0,703) + 1172(х - 0,703)
3
]⋅I
10
(0,703; х) - 135,7 + 1208х - 442,4х
2
; (20)
у = [-4511(х - 0,37)
3
- 12622(х - 0,37)
4
]⋅I
10
(0,37; х) + [-856,9(x - 0,703) + 874,9(x –
- 0,703)
3
]⋅I
10
(0,703; х) - 133,9 + 1205х – 441,8х
2
; (21)
y = [-869,8(х – 0,703) + 1188(х - 0,703)
3
- 1918(х - 0,703)
5
- 3967(х – 0,703)
8
]⋅
⋅ I
10
(0,703; х) – 134,8 + 1206х - 441,3х
2
. (22)
СО остаточной ошибки уравнения (20) S
ост
= 0,96
о
C с числом степе ней свободы f
ост
= 17;
уравнения (21) - S
ост
= 1,03°С с f
ост
= 18; уравнения (22) - S
ост
= 0,89
o
C с f
ост
= 18. Гипотеза об
адекватности всех трех сплайнов не отклоняется, поскольку соответствующие расчетные значения
5
критерия Фишера (1,20; 1,38; 1,03) меньше критических при 5%-ном уровне значимости F (0,05;
17; 10) = 2,81 и F (0,05; 18; 10) = 2,79. На рис. 2 иллюстрируется высокая точность аппроксимации
кривой ликвидус сплайном (22). Как того и требует физико-химический смысл, в точке
кристаллизации двойной эвтектики (InSb + Sb) сплайны обеспечивают разрыв непрерывности
первой производной, в остальных точках функции аналитичны.
Литература
1. Едвабник И. Ю., Новик Ф. С., Цейтлин Н. А. Использование двухсторонних сплайнов для
аппроксимации сложных физико-химических кривых. Зав. лаб., 1985, т.51, №3, с. 54-57.
2. Завьялов Ю. С., Квасов Б. И., Мирошниченко В. Л. Методы сплайн-функций. –M.: Наука, 1980.– 352 с.
3. Пуарье Д. Эконометрия структурных изменений. - M.: Финансы и статистика, 1981. - 183 с.
4. Park S. H. // Technometrics. – 1978. - V. 20. - №2. - Р. 151 - 154.
5. Новик Ф. С., Цейтлин H. А., Авраменко Э. H. // Заводская лаборатория. - 1981. - №1. - С. 48 - 55.
6. Wold S. // Technometrics. – 1974. - V. 16. - № 1. - P. 1 - 11.
7. Hultgren R. а. о. Selected Values of Thermodynamic Properties of Metals and Alloys. - N. Y.: John Wiley,
1963. - 711 p.
8. Lui T., Perrety E. // Trans. ASM. – 1952. - V. 44. - P. 539 - 541.
9. Себер Дж. Линейный регрессионный анализ. – M.: Мир, 1980. - 456 с.
1
6.1.4. Статистическое оценивание параметров электрохимической кривой,
характеризующей область пассивного состояния металла в растворе электролита
Кислое лицо - первый признак коррозии организма. (Из интернета)
В одноименной работе (Цейтлин Н. А., Заяц И. И., Аверченко В. И., Ланцберг Н. Г. - В кн.:
Коррозия и защита аппаратуры в производствах основной химии. Труды, т. 60/НИОХИМ.
Харьков, 1987. с. 91-101.) описана процедура построения интервальной оценки вектора
коэффициентов регрессии, которые, в свою очередь, интерпретируются как физические
константы.
Известно [1], что исследование кинетики анодной, или катодной электрохимической
реакции начинается с установления связи между удельной скоростью процесса, выражаемой через
плотность тока, и сдвигом потенциала от равновесного значения. Зависимость между потенциалом
и плотностью тока (см., например, рис. 1а) называют
электрохимической кривой (ЭК)
.
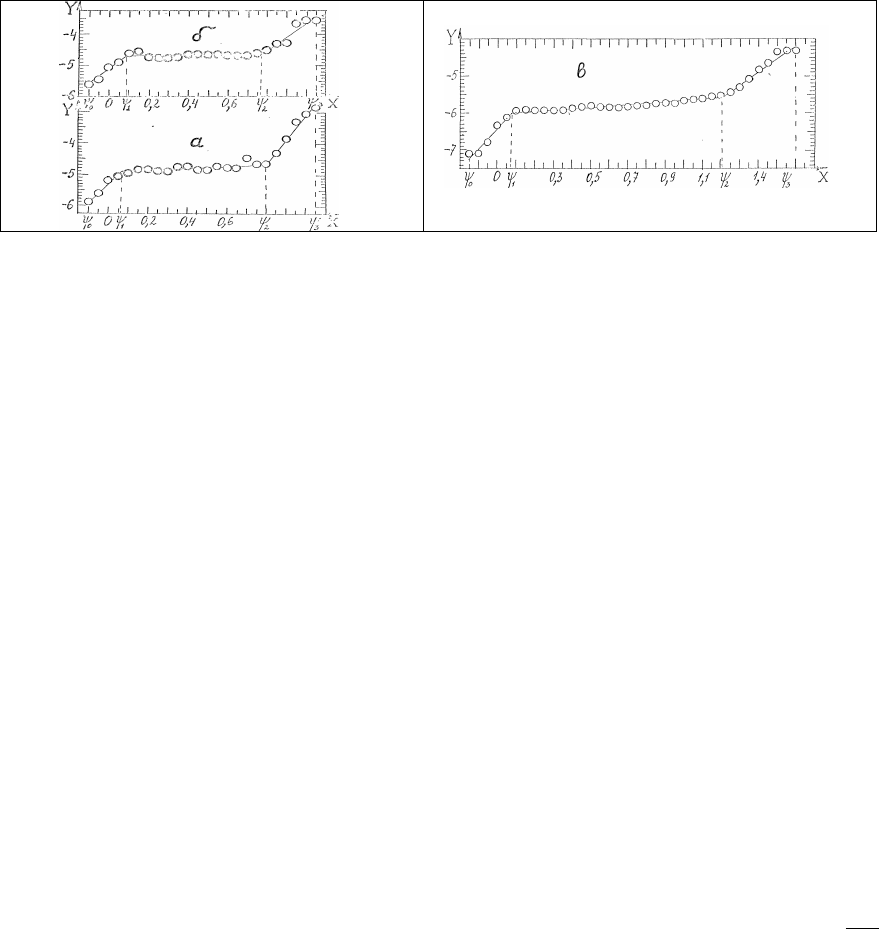
Рис. 1. Электрохимические кривые:
х – потенциал коррозии, В; Y = -lgJ - отклик, J - плотность тока, А/см
2
; точки – результаты
наблюдений; линии построены методом наименьших квадратов; а, б – результаты параллельных опытов с
образцами типа А; в – результаты опытов с образцами типа В.
Рассмотрим три гладких участка ЭК, разделенных двумя узлами ψ
1
и ψ
2
, где ψ
1
– точка
начала пассивного состояния и ψ
2
– точка перепассивации. С помощью этих точек определяют
начало и конец области пассивного состояния [1].
Традиционно ЭК строят следующим образом [1]. Измеряемые в опытах значения
потенциала коррозии (Х, В) и плотности тока (J, A/см
2
) наносят на график в координатах –lgJ – X;
с помощью лекал полученные точки сглаживают кусочно-гладкой функцией; на рисунке находят
значения абсцисс узлов ψ
1
и ψ
2
.
Такое положение удовлетворяло исследователей потому, что точечные (однозначные)
оценки параметров ψ
1
и ψ
2
были достаточно точными для практических целей. В работе в
терминах теории проверки гипотез будет показано, что это действительно так: «глазомерный»
способ оценивания параметров ψ
1
и ψ
2
соизмерим по точности с методом наименьших квадратов
[2]. Однако при точечном оценивании статистических параметров теряется существенная
информация об ошибке оценок и вместе с ней – возможность проверки различных
статистических гипотез (об адекватности аппроксимации, о значимом различии между
результатами разных экспериментов, о согласии опыта с теорией и т. п.)
Таким образом, для обработки ЭК необходимо наряду с точечными получать и
интервальные [2] оценки параметров.
В настоящее время стремительно развиваются методы автоматизации эксперимента [3]. Эти
методы обеспечиваются специальной техникой (микропроцессорами, интерфейсами и т. п.) и
математическим обеспечением.
Поскольку ЭК получают на электронных приборах, оборудование этих приборов
микропроцессорами позволит полностью автоматизировать процесс построения и обработки ЭК.
В основе разрабатываемого метода математической обработки ЭК лежит теория
регрессионного анализа [2, 4].
Примем в качестве отклика функцию Y = -lgy. Тогда результаты N измерений y
i
и x
i
(
1,
iN
= )
можно представить как выборку{Y
i
, X
i
}
i=1
объемом N элементов (точек) (Y
i
X
i
). Запишем
регрессионную модель процесса в виде
-lgy = Y = ϕ(x) + ε (1)

2
где ϕ(x) – функция регрессии; ε - случайная нормальная ошибка модели, имеющая нулевое
математическое ожидание и дисперсию
2
Y
σ
.
В качестве функции регрессии ϕ(x) необходимо использовать функцию, определяемую на
сетке (ψ
0
, ψ
1
, ψ
2
, ψ
3
), где ψ
i
– особые точки электрохимической кривой; ψ
0
= min{x
i
}, ψ
3
= max{x
i
}
- точки начала и конца кривой;
ψ
1
,
ψ
2
- точки разрыва первого рода непрерывности первой
производной функции. На области (ψ
1
, ψ
2
) функция ϕ(x) линейна, а на участках ψ
0
, ψ
1
) и (ψ
2
, ψ
3
) (в
общем случае) она совпадает с многочленами степени а ≥ 1 и b ≥ 1 соответственно.
Сформированным требованиям в точности удовлетворяет двухсторонняя сплайн-функция
[5; Ф(8)Р6.1.2]
()()()()()
3
2
1101122012
13
,,
aab
jja
aaj
jja
xxIxxIx
ϕψψβββψψ
++
−−
++
==+
=−+++−
∑∑
, (2)
где β
j
– коэффициенты регрессии; I (⋅) – единичные ступенчатые функции;
()()
12
101012
12
1 npu x;0 npu ;
,,
0 npu ; 1 npu .
x
IxIx
xx
ψψ
ψψ
ψψ
≤≤
==
>>
(3)
Действительно, функция ϕ(x) (2) на первом участке [ψ
0
, ψ
1
) электрохимической кривой
представляет собой полином порядка а ≥ 1;
()
112
1
a
j
jaa
j
xx
ψβββ
++
=
−++
∑
; (4)
на участке пассивного состояния [
ψ
1
,
ψ
2
) – прямую
β
а+1
+ β
а+2
х; (5)
на третьем участке [ψ
2
, ψ
3
) – параболу порядка b ≥ 1;
()
3
2
122
3
ab
ja
aa
ja
xxββψ
++
−−
++
=+
++−
∑
. (6)
Частным случаем функции (2) при а = b = 1, является кусочно-линейная функция
ϕ
(x) = I
10
(
ψ
1
, x)(x -
ψ
1
)
β
1
+
β
2
+
β
3
x + I
01
(
ψ
2
, x)(x -
ψ
2
)
β
4
. (7)
Кусочно-линейная аппроксимация ЭК используется чаще всего [1]. Поэтому в дальнейшем в
качестве аппроксимирующей функции будет использована двухсторонняя сплайн-функция (7).
Поскольку параметры
ψ
1
и
ψ
2
входят в функцию (7) не линейно, их, а заодно и
β
j
(
1,4
j = ),
можно оценить итерационным методом Марквардта [4, 6]. Для расчетов по этому методу
необходимо использовать производные функции регрессии по параметрам и значения
оцениваемых параметров в первом приближении. Производные функции (7) имеют вид
(
)
(
)
(
)
()()()
1234
12
10112
01211014012
,;1;;
,;,;,.
Ixxxx
IxIxIx
ββββ
ψψ
ϕψψϕϕϕψ
ψϕβψϕβψ
′′′′
=−===−×
′′
×=−=−
(8)
Первые приближения параметров рекомендуется получать так. С помощью линейки на
графике необходимо изобразить кусочно-линейную функцию, определить координаты точек
начала (ψ
0
, Y
0
), конца (ψ
3
, Y
3
) и узлов (ψ
1
, Y
1
) и (ψ
2
, Y
2
) этой функции.
Далее необходимо вычислить коэффициенты β
i
формулы (7):
β
3
= (Y
2
–Y
1
)(ψ
2
-ψ
1
); β
2
= Y
1
-β
3
ψ
1
;
1023001
()/();
Y
βββψψψ
=−−−
4323334
()/().
Y
βββψψψ
=−−−
(9)
Нелинейное оценивание параметров модели (2) сопровождается расчетом
среднеквадратичного отклонения (СО) остаточной ошибки S
0Y
и верхнего α-предела S
0Y
α
СО
отклика – параметра ЭФР для приближенной 95%-ной доверительной области [4] параметров
ψ
1
и
ψ
2
, причем:
(
)
0,5
1
00,,
1()
YYmNm
SSmNmF
αα
−
−
=+− , (10)
где т = 6 – число оцениваемых параметров; F
m;N-m;
α
- верхний α-предел статистики Фишера;
с т = 6 и N - т степенями свободы; α = α
k
– заданный уровень значимости [Т2Р1]; 1 - α
k
–
доверительная вероятность.
Для практических целей в качестве совместной доверительной области удобно использовать
доверительные прямоугольники [4]:
111
ˆˆ
;
HB
ψψψ
≤≤
222
ˆˆ
HB
ψψψ
≤≤
; (11)
где:
ˆ
iH
ψ
,
ˆ
iB
ψ
- нижние и верхние 100 (1 - α
k
)%-ные границы доверительных интервалов для
ψ
i
(i = 1, 2).

3
Замечание. В «старые времена» построение точной совместной доверительной области для
большого числа параметров ЭФР было проблематично [4]. Однако в настоящее время такую
область уже можно строить методом бутстреп [11]. Скорость вычислений на современных ЭВМ
уже столь высока, что большое количество расчетов теперь не является существенной преградой
для использования этого метода. А для описания точной совместной интервальной оценки
всех параметров функции регрессии (7) простыми формулами достаточно воспользоваться
тем же методом, который применяется для окаймления области определения регрессионной
модели [Р6.2.1].
Поскольку нас всё же интересуют лишь два параметра -
ψ
1
и
ψ
2
, то приближенно
совместную доверительную область для этих параметров можно построить, фиксируя
остальные параметры на уровнях, соответствующих их оценкам, полученным методом
наименьших квадратов (МНК-оценками). Можно ожидать, что оценки параметров ψ
1
и ψ
2
будут
независимыми.
Совместные интервальные оценки параметров ψ
1
и ψ
2
надежно, с высокой заранее заданной
вероятностью (1 – Р) накрывают истинные значения параметров ψ
1
и ψ
2
. Это обстоятельство, в
частности, можно использовать для проверки статистических гипотез. Так, можно предположить,
что различие оценок
1
ˆ
ψ
и
2
ˆ
ψ
узлов
ψ
1
и
ψ
2
случайно, то есть нулевой гипотезы Н
0
:
ψ
1
=
ψ
2
против
альтернативной гипотезы Н
1
:
ψ
1
<
ψ
2
. Можно также проверить, случайно ли различие оценок
1
ˆ
a
ψ
и
2
ˆ
a
ψ
одной ЭК и оценок
1
ˆ
b
ψ
и
2
ˆ
b
ψ
другой ЭК (см., например, ЭК на рис. 1а, б).
Соответствующая нулевая гипотеза имеет вид
Н
0
: Н
01
∩
Н
02
; Н
01
: ψ
11
= ψ
12
; Н
02
: ψ
21
= ψ
22
, (12)
где вторые индексы (1 и 2) относятся к данным на рис. 1а и 1б соответственно.
Альтернативная гипотеза имеет вид
Н
1
: Н
11
∪
Н
12
; Н
11
: ψ
11
≠ ψ
12
; Н
12
: ψ
21
≠ ψ
22
. (13)
Здесь Н
0i
и Н
1i
,
1,2
i = - две пары частных нулевых и альтернативных гипотез.
Аналитический метод проверки гипотезы (12) [10, с. 88] сложен и не дает наглядного
представления о сравниваемых величинах. Для большей наглядности эти гипотезы можно
проверить методом доверительных интервалов (ДИ-методом) [2, 9; Р1.2]. Например, для проверки
нулевой гипотезы (12) на рисунке изображают совместные интервальные оценки параметров
ψ
1i
и
ψ
2i
с доверительной вероятностью 1 – Р. Если доверительные области пересекаются, гипотеза Н
0
не отклоняется; если не пересекаются, то Н
0
отклоняется.
Зависимость доверительной вероятности 1 – Р для двух двусторонних альтернативных
гипотез Н
1i
(13) от критического уровня значимости
α
k
при большом числе опытов N > 20
определяется в неявном виде [9] как Z
P/2
= Z
α/4
⋅
2
-0,5
, где Z
b
– верхний b-предел нормированного
нормального распределения. Из этой формулы при обычно принимаемом уровне значимости α
k
=
0,05 получим [9] Z
0,05/4
= 2,24; Z
Р/2
= 1,584; Р/2 = 0,0565: 1 – Р ≈ 0,9.
Для проверки гипотез об адекватности аппроксимации необходимо получить несмещенную
оценку дисперсии отклика [4, с. 37]. Обычно такую оценку получают по результатам
параллельных наблюдений [4, с. 34]. (Она называется дисперсией «чистой» ошибки, или
дисперсией ошибки воспроизводимости отклика). Однако при построении ЭК выполнение
параллельных наблюдений затруднительно [1]. Поэтому несмещенную оценку дисперсии отклика
будем строить, воспользовавшись известной закономерностью [1]: средний участок
электрохимической кривой между узлами
ψ
1
и
ψ
2
, характеризующий область пассивного
состояния, является точно линейным. Для этого используются точки с абсциссами
[
]
1"2
ˆˆ
,
iBH
xVψψ∈= , где V - «гарантированная область линейного участка электрохимической
кривой (считаем, что
1
ˆ
B
ψ
<
2
ˆ
H
ψ
).
Остаточная дисперсия
2
0
YL
S
, найденная по остаткам линейной аппроксимации точек (5) на
области V является несмещенной оценкой дисперсии
2
Y
σ
отклика. Проще всего оценить СО S
0YЛ
по
формуле [2, 4]
S
0YЛ
= (1 – r
2
)
1/2
S
Yоб
(14)
где: r – коэффициент парной корреляции на области V; S
Yоб
- общее СО отклика Y на области V.

4
Гипотеза об адекватности модели (1) формулируется как гипотеза об однородности
дисперсий
2
0
Y
S
и
2
0
YL
S
(см. гипотезу № 17 [Т3Р1]) и проверяется с помощью α-критерия Фишера.
Разработанная методика оценивания параметров электрохимической кривой в будущем
может быть реализована на системе прибор – ЭВМ – эксперт (интерфейс включает пульт
управления и дисплей). Прибор предназначен для получения выборки, интерфейс – для расчета
параметров кривой; эксперт выбирает области определения (
ψ
0
,
ψ
3
) модели, планирует объем N
выборки
{}
1
,
N
ii
i
YX
=
, задает нулевое приближение узлов
ψ
1
,
ψ
2
, контролирует операции измерения
и расчета параметров ЭК.
Программа для ЭВМ должна реализовать следующие действия.
1. Ввод в ЭВМ исходных данных от прибора
{}
1
,
N
ii
i
YX
=
; от оператора
(0)
1
ψ
,
(0)
2
ψ
и
критический уровень значимости α
k
для проверки гипотез.
2. В первом приближении – выполнение структурной и параметрической идентификации ЭК
методом линейного регрессионного анализа. Проверка гипотез о значимости параметров β
j
функции (2), относящихся к каждому участку кривой.
Если кривая не имеет трех четко выраженных участков (например, первого), то
соответствующие параметры (например, β
j
,
1,
ja
= ) будут незначимы. Тогда программа должна
потребовать возврата в п. 1 для получения новых данных.
Если параметры
β
j
функции (2) для каждого участка кривой значимы (кривая имеет три
четко выраженных участка), то расчет продолжается.
3. Во втором приближении методом нелинейного оценивания необходимо уточнить оценки
β
j
, ψ
1
и ψ
2
параметров кривой.
4. Построить интервальные оценки параметров
ψ
1
,
ψ
2
.
5. По точкам {Y
i
, X
i
} из области пассивного состояния оценить дисперсию отклика и
проверить адекватность модели.
6. Печатать численные значения результатов расчетов; на дисплей вывести графики кривой
и интервальных областей.
Пример. Результатами наших наблюдений (см. рис. 1а, б, в) являются три выборки объемом
N
а
= N
б
= 24, точки, полученные при одинаковых условиях и N
в
= 36 точек – для одного опыта,
выполненного при других условиях.
Полученные точки нанесли на график; с помощью карандаша и линейки построили быстрые
оценки кусочно-линейных функций регрессии, состоящих из трех прямых, проходящих через
следующие точки
Рис. 1а Рис. 1б Рис. 1в
i
0
ψ
i
-0,12
Y
i
6,00
ψ
i
-0,08
Y
i
5,50
ψ
i
-0,15
Y
i
7,20
1 0,05 4,90 0,05 4,75 0,072 5,97
2 0,80 4,65 0,85 4,50 1,22 5,51
3 1,00 3,05 1,10 3,10 1,55 4,20
В результате вычислений по формулам (9) получили ЭФР вида (7) в первом приближении
для данных на рис. 1 а, б и в соответственно:
(
)
x
ϕ
%
= -6,12(x – 0,05)I
10
(0,05; x) + 4,92 – 0,333x – 7,68(x – 0,8)I
01
(0,8; x); (15)
(
)
x
ϕ
%
= -5,42(x – 0,05)I
10
(0,05; x) + 4,77 – 0,31x – 5,32(x – 0,8)I
01
(0,8; x); (16)
(
)
x
ϕ
%
= -5,14(x – 0,072)I
10
(0,072; x) + 6,00 – 0,40X – 3,58(x – 1,219)I
01
(1,21, x). (17)
Далее по программе нелинейного МНК [6] на ЭВМ «Наири-2» получили окончательно для
данных на рис. 1 а, б и в соответственно:
(
)
x
ϕ
%
= -5,48(x – 0,06)I
10
(0,06; x) + 4,96 –0,35x – 7,6(x – 0,8)I
01
(0,8; x); S
oY
= 0,091; S
Yα
= 0,126; (18)
(
)
x
ϕ
%
=-4,77(x – 0,089)I
10
(0,089; x) + 4,7–0,059x – 4,31(x – 0,77)I
01
(0,77; x); S
oY
= 0,1; S
Yα
= 0,13; (19)
(
)
x
ϕ
%
=-5,14(x–0,074)I
10
(0,074; x)+6,03–0,363x–3,303(x–1,206)I
01
(1,206; x); S
oY
=0,07; S
Yα
=0,1. (20)
Все оценки параметров в формулах (18) – (20) статистически значимы на уровнях
значимости, меньших 10
-4
. По уравнениям доверительных областей (10) были построены
5
двумерные сечения (эллипсы на рис. 2) в плоскости узлов ψ
1
- ψ
2
при значениях остальных
параметров, равных их МНК-оценкам.
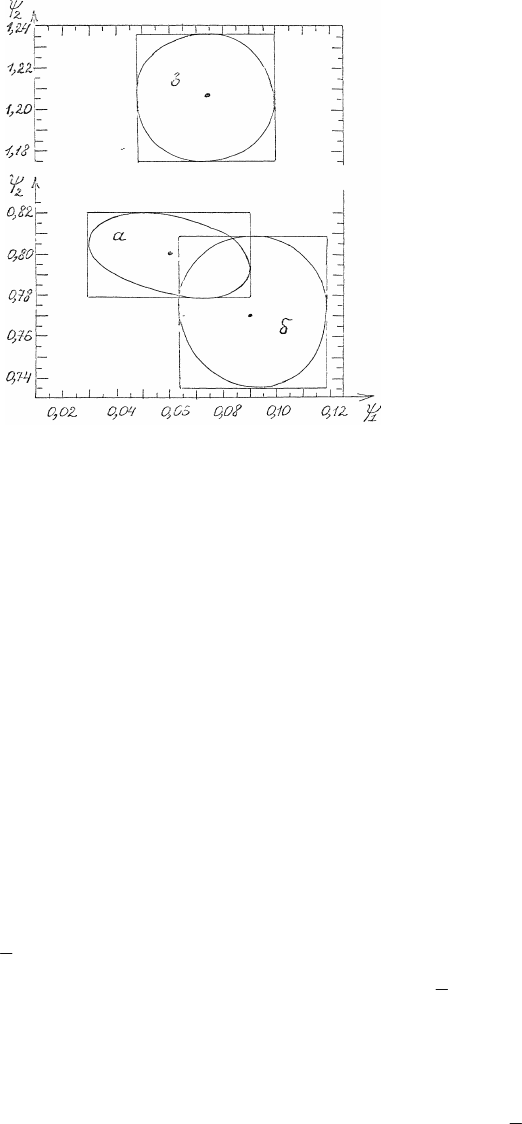
Рис. 2. Совместная 90%-ная интервальная оценка параметров
ψ
1
и
ψ
2
- нижней и верхней границ
зоны пассивного состояния на электрохимической кривой по данным на рис. 1а, б, в.
Поскольку для анализа удобно иметь раздельные интервальные оцени для каждого
параметра ψ
1
и ψ
2
, были построены минимальные доверительные прямоугольники, окаймляющие
доверительные области (см. рис. 2).
- для ЭФР (18): 0,03 ≤ ψ
1
≤ 0,09; 0,78 ≤ ψ
2
≤ 0,82; (21)
- для ЭФР (19): 0,06 ≤ ψ
1
≤ 0,12; 0,74 ≤ ψ
2
≤ 0,81; (22)
- для ЭФР (20): 0,049 ≤ ψ
1
≤ 0,099; 1,175 ≤ ψ
2
≤ 1,236. (23)
Доверительные области, ограниченные эллипсами (см. рис. 2), имеют почти «канонический»
вид, что указывает на слабую корреляцию ψ
1
и ψ
2
.
Доверительные области и прямоугольные интервальные оценки по площади почти
одинаковы, поэтому на практике вполне можно пользоваться доверительными интервалами (21) -
(23). «Гарантированные» области v линейных участков электрохимических кривых содержат по N
0
точек; для данных на рис. 1а: 0,09
≤
x
i
≤
0,76; N
0
= 14; для данных на рис. 1б: 0,12
≤
x
i
≤
0,74; N
0
=
14; для данных на рис. 1в: 0,099 ≤ x
i
≤ 1,175; N
0
= 21.
Несмещенные оценки СО отклика получили путем расчетов по формуле (14):
S
0Yла
= 0,117(1 – 0,7
2
)
0,5
= 0,084 и аналогично S
0YЛб
= 0,054 с f
0YЛ
= 12 степенями свободы;
S
0YЛв
= 0,07; f
0YЛв
= 19.
Поскольку полученные S
0YЛj
, j ∈ (а, б, в) однородны (статистика α-критерия Фишера,
определенная по формуле [7; Ф(52)Р1], равна
ˆ
F
α
= 0,14), можно определить среднее взвешенное
значение СО ошибки отклика
0
YL
S
= 0,07 с 43 степенями свободы.
Сравнение остаточных дисперсий
2
0
Y
S
формул (18) – (20) c дисперсией
2
0
YL
S
с помощью α-
критерия Фишера [7; Ф(48)Р1] показывает, что эти формулы адекватны результатам наблюдений
на высоких уровнях значимости, больших 0,2.
Проверим теперь, насколько «глазомерный» метод графической аппроксимации соизмерим
по точности с методом наименьших квадратов. Для этого проверим качество формул первого
приближения (15) – (17). По методике [8] находим систематические составляющие
j
e
ошибок
этих формул: S
ea
= 0,1; S
eб
= 0,12; S
eв
= 0,1.
Уровни значимости систематических ошибок, равные 0,1, 0,4 и 0,6 достаточно велики,
чтобы с высоким уровнем ответственности за выводы [7, 8; Т2Р1] говорить о том, что
систематические составляющие ошибок аппроксимаций (15) – (17) незначимы.
Уровни значимости α-критерия Фишера [7, 8] адекватности формул (15) – (17) равны 0,03,
0,002 и 0,02 соответственно (получены с помощью статистик Фишера F
а
= (0,1/0,07)
2
= 2; F
б
= 2,9 с
18 и 43 степенями свободы каждая; F
в
= 2 с числами степеней свободы 30 и 43). Следовательно,
6
лишь с «малой ответственностью за выводы» [7; Т2Р1] все же можно говорить об адекватности
«глазомерных» аппроксимаций (15, 16, 17) результатам наблюдений.
Большой интерес представляет сравнение оценок параметров
ψ
1
и
ψ
2
электрохимических
кривых. Для этого воспользуемся ДИ-методом [9]. Сравнение изображений совместных 90%-ных
доверительных областей для параметров
ψ
1
и
ψ
2
на рис. 2 показывает, что оценки параметров
ψ
1
и
ψ
2
по данным на рис. 1а и 1б отличаются незначимо (совместные доверительные области а и б
пересекаются); оценки параметра ψ
1
на всех трех кривых отличаются незначимо (проекции трех
совместных доверительных областей на ось
ψ
1
пересекаются).
Выводы.
Показано, что наряду с точечным оцениванием параметров электрохимической кривой
(которое возможно «глазомерным» способом) необходимо осуществлять интервальное
оценивание этих параметров (обеспеченное описанной выше методикой).
Литература
1. Скорчеллетти В. В. Теоретические основы коррозии металлов. – Л.: Химия, 1973. – 264 с.
2. Цейтлин Н. А. Методы статистической обработки результатов наблюдений при пылегазовых
замерах. – Харьков: НИОХИМ, 1981. – 53 с. (Рукопись деп. в ОНИИТЭХИМ г. Черкассы 7 августа 1981 г.
№725XII-Д81). / Библ. Указатель ВИНИТИ. Деп. Рукописи. – 1981. - №12. – С. 139.
3. Шлыкова В. П. Планирование эксперимента и автоматизация научных исследований:
Библиографический указатель отечественной и иностранной литературы за 1979 – 1982 г. г. – М.: Изд. МЭИ,
1983. – 164 с.
4. Дрейпер Н., Смит Г. Прикладной регрессионный анализ. – М.: Статистика, 1973. – 392 с.
5. Едвабник И. Ю., Новик Ф. С., Цейтлин Н. А. Использование двухсторонних сплайнов для
аппроксимации сложных физико-химических кривых // Зав. лаб. - №3. – Т. 51. – 1985. – С. 54 – 57.
6. Ланцберг Н. Г., Скоробогатько Ю. В., Цейтлин Н. А. Нелинейное оценивание на ЭВМ «Наири-2»
параметров уравнений регрессии с приложением к задачам физической химии. – Харьков: НИОХИМ, 1980.
– С. 54. (Рукопись деп. В ОНИИТЭХИМ г. Черкассы 25 января 1979 г. №725XII-Д80). / Библ. указатель
ВИНИТИ. Деп. Рукописи. – 1980. - №11. – С. 97.
7. Цейтлин Н. А. Применение методов математической теории эксперимента в содовой промыш-
ленности. Обзорная информация. Серия: Содовая промышленность. – М.: НИИТЭХИМ, 1984. – 36 с.
8. Зайцев И. Д., Цейтлин Н. А., Чайка В. П. Статистический анализ методов расчета параметров
физико-химических свойств многокомпонентных растворов электролитов // Хим. пром-сть. – 1983. - №8. –
С. 500 – 503.
9. Цейтлин Н. А. Проверка гипотез методом доверительных интервалов // В кн. Методы
математической статистики в основной химии / Труды НИОХИМ. – Т. 55. – Харьков, 1981. – С. 82 – 89.
10. Болч Б., Хуань К. Дж. Многомерные статистические методы для экономики. – М.: Статистика,
1979. – 317 с.
6.1.5. Физхимия. Формула для расчета температуры замерзания водного раствора
электролита по активности воды
Эта теорема пригодна лишь для спора о ней (Георг Кристоф Лихтенберг)
В одноимённой работе [Цейтлин Н. А., Зайцев И. Д. Журн. физич. химии №7, т. 59, 1985,
с.1809 - 1810.] предпринят поиск подходящей структуры регрессионной функции для
аппроксимации зависимости температуры замерзания многокомпонентного водного раствора
электролита от активности воды в растворе. В основу структуры регрессионной функции
пытались положить результат интегрирования уравнения Клаузиуса - Клапейрона. Однако
наиболее точную аппроксимацию получили с помощью эмпирической формулы.
Нижней температурной границей области существования водных растворов электролитов
является температура T замерзания растворителя. Эта температура соответствует состоянию
раствора, при котором давление насыщенного пара воды надо льдом совпадает с давлением
насыщенного пара над раствором. Если вычесть из уравнения Клаузиуса - Клапейрона для
процесса сублимации льда [1] другое уравнение Клаузиуса - Клапейрона для процесса испарения
чистой воды, получим
(
)
(
)
2
1
//ln RTLdTad =
, (1)
где а - активность воды: Т
1
- температура; L - теплота плавления льда; R = 0,0019872
ккал/моль [1].
Интегрированием уравнения (1) при L = const получим
ln a = -L(T
0
- T)/(RTT
0
), (2)
где T
0
, T - температуры замерзания растворителя и раствора соответственно. При T
0
= 273,16
K, L = l,4363 ккал/моль уравнение (2) имеет вид
T = 313,9/(1,1491 - lga). (3)
Интегрируя уравнение (1) при L = L
o
T
1
/T
0
, где L
o
- теплота плавления льда при температуре
T
0
, получим
T = 273,16 а
0,3779
. (4)
Поскольку в уравнениях (3) и (4) переменная а зависит от температуры T [1], их приходится
решать относительно T методом итераций.
Здановский А. Б. [2] по экспериментальным данным построил зависимость между
температурой замерзания воды в растворе и активностью воды а
0
при 298 К. Затем он
аппроксимировал эту зависимость уравнением вида (3), соответственно скорректировав
коэффициенты
T = 320,8/(1,1750 - lg а
0
). (5)
Уравнение (5) имеет небольшую погрешность лишь в малой области а
0
∈ (0,85;1) (рисунок).
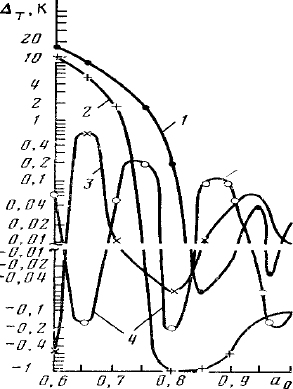
Рисунок. Погрешность аппроксимаций зависимости температуры замерзания воды в
многокомпонентном растворе электролита от активности воды в растворе при 278 К по данным
[2]: 1 - уравнение (5), 2 - (4), 3 - (6), 4 - (7).
Для более точной аппроксимации экспериментальных данных в широкой области
температур в уравнения типа (2) вводят эмпирические члены типа β
0
/(β
1
+ Т), β
2
Т, β
3
Т
2
, β
4
lnT, β
5
T
-2
[3, 4].
Практический интерес представляет такая форма эмпирического уравнения, которая, во-
первых, достаточно точна и, во-вторых, решается относительно T в явном виде. Этим условиям
удовлетворяет формула Ранкина [5]. По экспериментальным данным [2] получаем методом
наименьших квадратов оценки, коэффициентов формулы Ранкина
Т = 365,9703/[l,82133 - (lg а
0
+ 0,231904)
0,5
]. (6)
Это уравнение немного точней уравнения (5) (см. рисунок), однако область его определения
а
0
∈ (0,586; 1) ограничена снизу, так как выражение под корнем должно быть больше нуля.
Построим зависимость Т = f(а
0
) в координатах T
-1
- lga
0
; получилась кривая, которую можно
аппроксимировать параболой третьего порядка:
T = 10
7
/[36608 – 32979 lga
0
– 74302(lga
0
)
2
– 607310⋅(lga
0
)
3
]. (7)
Это уравнение точнее предыдущих (см. рисунок); остаточная среднеквадратичная ошибка
равна 0,16 К (если а
0
определять без ошибки) Значение а
0
для (1 + п)-компонентного водного
раствора вычисляется по формуле Эзрохи [6], коэффициенты которой для ряда солей приведены,
например, в работах [6, 7].
Автор выражает признательность к. т. н. Н. Г. Ланцбергу за участие в теоретической части
работы.
Литература
1. Киреев В. А. Краткий курс физической химии. M.: ГХИ, 1963. 648 с.
2. Здановский А. Б. Журн.
физ. химии. 1977. т. 51. № 9. с. 2209. 3. Зацемина Г. H. Свойства и структура воды. M.: Изд-во МГУ, 1974.
168 с.
4. Праусниц Дж. М. Машинный расчет парожидкостного равновесия многокомпонентных смесей. M.:
Химия, 1971. 216 с. 5. Цейтлин H. А. Журн. прикл. химии. 1973. т. 46. № 11. с. 2488. 6. Эзрохи Л. Л. Метод
расчета упругости пара солевых растворов. Труды ВНИИГа, 1959. № 36. с. 37 - 67.
7. Цейтлин H. А.,
Горбунова С. В. Деп. в ОНИИТЭХИМ, Черкассы, № 394ХII-Д81.
