Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

1
6.1.6. Построение многомерных сплайнов при аппроксимации сложных зависимостей
Чем сложнее задача, тем проще её не решать (Вадим Зверев)
При аппроксимации сложных зависимостей широкое применение получили сплайн-
функции [1, 2]. B большинстве работ используются одномерные сплайны [3]. Выбор узлов
сплайна в этом случае облегчается наглядностью материала. Значительно сложнее строить
многомерные сплайны. Здесь обычно рассматривают сетки узлов по каждой переменной,
образующие многомерную решетку [2]. Однако при большой размерности задачи сплайны
содержат много параметров, подлежащих оцениванию. Кроме того, сложно выбрать узлы
сплайна, поскольку графически изобразить аппроксимируемую функцию зачастую довольно
сложно. Н. Г. Ланцберг и Г. А. Статюха [1] предложили оригинальный метод построения
многомерных сплайнов, лишённый названных недостатков.
Экспериментальные данные разбиваются на несколько групп. В каждую группу
отбираются опыты, значения отклика в которых отличаются не очень сильно. Методами
дискриминантного анализа находятся разделяющие эти группы поверхности, после чего
строится многомерный сплайн, «сшитый» вдоль этих поверхностей.
Пусть опыты разбиты на две группы и найдена разделяющая эти группы гиперплоскость
L(
x
r
) = 0, (1)
где
x
r
- вектор независимых переменных (факторов). В каждой области можно построить полином
второго порядка от n переменных. Оба полинома можно записать одним уравнением
()
(
)
()
(
)
212
,,
SxPxIxGx
θβ
=+
rr
rrrr
, (2)
где
(
)
2
,
Px
θ
r
r
- полином второго порядки от n переменных с вектором параметров
θ
r
,
(
)
2
,
Gx
β
r
r
-
«добавочный» полином второго порядка с вектором параметров
β
r
,
(
)
1
Ix
r
- функция
переключатель;
()()()()
11
0, npu 0;1, npu 0.
IxLxIxLx
=≥=<
rrrr
(3)
Полиномы будут сшиты на границе, если
(
)
2
,
Gx
β
r
r
= 0 при L(
x
r
) = 0. Отсюда получим
уравнение сплайна
()
(
)
()()
(
)
21
,,
SxPxIxLxRx
θβ
=+
rr
rrrrr
;
(
)
0
1
,
n
ii
i
Rxx
βββ
=
=+
∑
r
r
. (4)
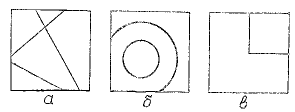
Формула (4) легко обобщается на случай К линейных границ (см. Рис., а)
Рисунок. Примеры разбиения факторного пространства на участки гладкой аппроксимации:
а - прямыми; б - окружностями; в - ломаной.
()
(
)
()()
(
)
2
1
,,
K
jjjj
j
SxPxIxLxRx
θβ
=
=+
∑
rr
rrrrr
, (5)
где
(
)
j
Lx
r
- левая часть уравнения j -й границы;
(
)
0
1
,
n
jjjiji
i
Rxx
βββ
=
=+
∑
r
r
,
()()()()
0, npu 0;1, npu 0.
jjjj
IxLxIxLx
=≥=<
rrrr
Число параметров m сплайна (5) равно
m = 0,5(n + 1)(n + 2) + K(n + 1). (6)
Если в задаче с К границами потребовать еще и непрерывности первых частных
производных по воем независимым переменным, получится сплайн
()
(
)
()()
2
2
1
,
K
jjj
j
SxPxIxLx
θβ
=
=+
∑
r
rrrr
. (7)
Разделить группы гиперплоскостью не всегда возможно. В частности, если в исследуемой
области имеется максимум или минимум, то группы целесообразно разделять замкнутой границей,
например, гиперсферой радиуса R
2
()()
2
2
1
,,0
n
ii
i
QxaRxaR
=
=−−=
∑
rr
, (8)
где
a
r
- вектор с координатами точки экстремума. Вектор
a
r
можно оценить, анализируя
неадекватную квадратичную аппроксимацию.
Уравнение сплайна с К концентрическими границами (см. Рис., б)
()
(
)
()
(
)
2
1
,,,
K
jRjjj
j
SxPxIxQxaR
θβ
=
=+
∑
r
rrrrr
. (9)
Например, при n = 2, К = 1
()()()()
22
222
011221112221212121122
,
R
SxxxxxxxIxxxaxaR
θθθθθθβ
=++++++−+−−
r
, (10)
где
()()()()()()
2222
22
121122121122
,0, npu ;,1, npu .
RR
IxxxaxaRIxxxaxaR
=−+−≤=−+−>
Радиус сферы R можно варьировать, добиваясь наилучшей аппроксимации.
Сшивать сплайны можно и на ломаной границе. Пусть граница образована двумя
пересекающимися гиперплоскостями с уравнениями L
1
(
x
r
) = 0 и L
2
(
x
r
) = 0.
Квадратичный сплайн, непрерывный на границе, имеет вид
()
(
)
()()()
212
,
SxPxLxLxIx
θβ=+
r
rrrrr
%
;
()
(
)
(
)
()()
12
12
0, npu 0 u 0;
1, npu 0 u 0.
LxLx
Ix
LxLx
>>
=
≤≤
rr
r
%
rr
(11)
Заметим, что всегда можно поменять знаки при L
1
(
x
r
) и L
2
(
x
r
) так, чтобы обеспечить их
положительность в одной из областей. Пример (см. Рис., в) n = 2, L
1
(x
1
, x
2
) = x
1
, L
2
(x
1
,x
2
) = х
2
,
()()
12121212
,0, npu 0 u 0;,1, npu 0 u 0.
IxxxxIxxxx
=>>=≤≤
%%
Уравнение сплайна
()
(
)
()
122121212
,,,,,
SxxPxxxxIxx
θβ=+
r
%
. (12)
Из формулы (12) видно, что полиномы, сшитые на такой ломаной границе, могут отличаться
лишь парным взаимодействием.
Заметим, что поверхностью второго порядка можно разделить опыты на группы, вообще
говоря, лучше, чем линейной, однако при этом сокращается число свободных параметров сплайна.
Пример. Данные взяты из работы Слотина [4]. Хорошее качество подгонки достигнуто там
за счет применения полиномиальных базисных функций с неизвестными параметрами. Для
определения этих параметров автор применил метод нелинейного оценивания. Но нелинейное
оценивание является сложной вычислительной задачей, особенно при больших размерностях
вектора параметров.
Применим наш метод для аппроксимации тех же данных. Визуально разделим опыты на две
группы. К первой группе отнесем 11 опытов, значения отклика в которых меньше 100. Вторую
группу составляют 4 опыта (№ 2, 6, 8, 14). Найдем уравнение гиперплоскости, разделяющей эти
группы в пространстве независимых переменных. Для этого используется стандартная программа
дискриминантного анализа из математического обеспечения ЕС ЭВМ [5].
Уравнение разделяющей плоскости
L (
x
r
) = 1,643 + 1,147(x
1
– x
2
) + 4,588 x
3
= 0; (13)
L (
x
r
) > 0 для первой группы опытов (кроме опыта № 4); L (
x
r
) < 0 для второй группы
опытов.
Лишь один опыт (№ 4) первоначально отнесенный к первой группе, в результате
дискриминации причислен ко второй.
Методом линейного регрессионного анализа получены оценки параметров сплайна,
непрерывно сшитого вдоль гиперплоскости (13)
ˆ
y
=92,2+14,9x
1
–23,4x
2
–14,9x
3
+10,0
2
1
x
+17,5
2
2
x
-24,1x
1
x
2
+46,3x
1
x
3
+63,3x
2
x
3
+
+(-4,5-8,4x
1
+13,8x
2
+3,0x
3
)I
1
(
x
r
)L(
x
r
). (14)
Остаточное среднеквадратическое отклонение S
ост
= 0,32 с числом степеней свободы f
ост
=2.
Сплайн с непрерывными первыми частными производными по всем переменным
ˆ
y
=97,6+25,1x
1
–18,2x
2
+82,7x
3
+10,1
2
1
x
+11,3
2
2
x
+97,0
2
3
x
-
-18,6x
1
x
2
+58,7x
1
x
3
-58,6x
2
x
3
-5,5I
1
(
x
r
)L
2
(
x
r
); S
ост
= 11,0; f
ост
= 4. (15)
3
Модель (14) значительно точнее как квадратичной модели с тройным взаимодействием
(S
ост
= 14,8; f
ост
= 4), так и модели Слотина, использующей преобразованные переменные
(S
ост
= 4,1; f
ост
= 4).
В данной работе рассмотрены лишь сплайны второй степени. Сплайны третьей степени
можно получить аналогично, но они будут содержать гораздо больше параметров. Для задач
небольшой размерности (2 - 3 переменных) применение этих сплайнов может быть
целесообразным.
Заметим, что для улучшения качества аппроксимации можно варьировать коэффициенты
разделяющих поверхностей, что аналогично варьированию узлов при построении одномерного
сплайна. Для решения этой задачи потребуется применение методов нелинейного оценивания.
Литература
1. Алберг Дж., Нильсон Э., Уолш Дж. Теория сплайнов и ее приложения. - М.: Мир,
1972. - 316 с.
2. Пуарье Д. Эконометрия структурных изменений. - M.: Финансы и статистика, 1981. -
184 с.
3. Wold S. Spline functions in data analysis, Technometrics, 1974, 16, р. 1-11.
4. Слотин Ю.С. Преобразование полиномиальных моделей. - Зав. лаб., 1980, № 1, с. 57-
64.
5. Математическое обеспечение ЕС ЭВМ. Вып. 15 / Ин-т математики АН БССР. -
Минск, 1978. – 199с.
1
6.2. Совершенствование программного обеспечения многомерного
регрессионного анализа
Техника скоро дойдет до такого совершенства,
что человек сможет обойтись без себя самого. (С. Е. Лец)
Разработанные нами во второй половине прошлого века некоторые алгоритмы и сервисные
процедуры к ПО ЭВМ по регрессионному анализу позволяли решать множество практических
задач фактически за один "подход" к ЭВМ. Результаты расчетов представляли собой целый
альбом распечаток матриц, графиков, формул, вариантов вычислений. В связи со сменой
поколений ЭВМ старые программы можно считать отжившими свой век, чего нельзя сказать о
нашем опыте, идеях и алгоритмах, описываемых в настоящем разделе.
6.2.1. Окаймление области определения регрессионной модели. Строительство.
Описание механических свойств шлама дистилляции содового производства.
Счастливы живущие без горизонта: их цели осязаемы, а пути к ним непродолжительны.
(Из интернета)
В одноимённой работе [Цейтлин Н. А., Дидович М. Я., Едвабник И. Ю., Рудай A. H.,
Куцына M. И., Козачек Л. Ф. Хим. технология, №6, 1983, с. 34-36.] на конкретном примере
описана попытка простого способа окаймления области определения E регрессионной
модели с помощью системы линейных неравенств.
Эта идея возникла так. В одной из предыдущих работ [6] по данным наблюдений за
работой промышленного объекта с помощью „стандартной“ программы линейного
регрессионного анализа [3] (в которой, в частности, область определения модели регрессии
задаётся довольно грубо - в виде гиперпараллелепипеда в факторном пространстве) был получен
ряд аппроксимирующих эмпирических функций регрессии (ЭФР). Затем технологи попытались
воспользоваться полученными формулами для решения задачи автоматического управления
производственным процессом. Оказалось, что в одних случаях „наши“ ЭФР дают
правдоподобные результаты, в других - просто неверные. Аналитическому статистику,
соисполнителю работы (автору), были предъявлены претензии, вполне справедливые, если
учесть, что область Е, на которой аппроксимирующие ЭФР справедливы, точно указана не
была. В созданном нами впоследствии ППП „РЕГАН“ [7 - 9] эта погрешность „стандартного“
программного продукта была устранена.
Отходы дистилляции содового производства в виде дистиллерной суспензии сбрасываются
в накопители (так называемые «белые моря»). Недостатками этого метода хранения отходов
являются: непроизводительное использование больших площадей плодородных почв; большие
эксплуатационные расходы, связанные с необходимостью обвалования «белых морей» высокими
дамбами; загрязнение окружающей среды отходами содового производства, попадающими в
естественные водоемы с паводковыми водами и в грунтовые воды при фильтрации из хранилищ.
В связи с этим актуальными являются задачи уменьшения площадей, занятых под хранение
отходов, уменьшения эксплуатационных расходов и улучшения экологических свойств
шламохранилищ.
Для решения этих задач необходимо иметь информацию о различных свойствах жидкой и
твердой фаз дистиллерной суспензии (твердой фазой является
шлам дистилляции - ШД
).
В работе исследовалась зависимость сопротивления шлама сдвигу
τ
от его физических
свойств - влажности W, объемной массы скелета
γ
, суммарной концентрации растворимых в воде
компонентов (CaSO
4
, Ca(OH)
2
, NaCl, CaCl
2
), H, а также от его состояния, характеризующегося
нормальным напряжением
σ
[1]:
τ
=
σ
tg
ϕ
+ C, (1)
где
ϕ
- угол внутреннего трения; С - структурное сцепление породы.
Зависимости коэффициентов tg
ϕ
и С от факторов lgW,
γ
и H в большинстве случаев
линейны [1].

2
Обозначим для простоты факторы z
1
=
σ
, z
2
= lgW, z
3
=
γ
, z
4
= H и отклик (зависимую
переменную) Y =
τ
. Искомую зависимость можно записать в виде регрессионной модели
4
0123123
114
iiijij
iij
Yzzzzzz
δδδδ
=≤<≤
=+++
∑∑∑
+ ε, (2)
где
δ
i
- неизвестные коэффициенты; ε ~ N(0, σ
Y
) – случайная ошибка модели.
По методике, принятой при исследовании механических свойств грунтов [2], было
проведено 18 опытов с первой партией шлама при концентрации солей H = 18 % (таблица).
Таблица
Результаты предварительных испытаний свойств шлама дистилляции содового производства
τ
, кПа
σ
, кПа
W, % опыт расчет
γ
, кг/м
3
98 48,5 113 106 1180
98 50,2 88 99 1170
98 50,0 93 98 1150
98 53,1 83 83 1070
98 55,8 74 73 1050
98 52,0 78 87 1070
196 49,8 147 151 1145
196 50,8 147 146 1133
196 49,2 147 156 1178
196 48,2 168 160 1175
196 49,7 157 153 1166
196 47,2 186 165 1192
392 46,5 275 265 1132
392 46,8 275 266 1142
393 45,1 294 287 1222
392 44,6 275 288 1213
392 43,9 294 294 1231
392 43,2 294 311 1308
Примечание.
σ
- нормальное напряжение, кПа; W - влажность, %;
τ
- предельное касательное
напряжение, кПа;
γ
- удельная масса скелета, кг/м
3
.
Статистические характеристики регрессионной модели (2) получены с помощью
стандартной программы линейного регрессионного анализа [3, 4]. После ряда пересчетов методом
Ефроимсона, получили следующую ЭФР
τ
ˆ
= b
0
+ b
1
γσ
+ b
2
lgW, (3)
где S
0
τ
= 0,10 кг/см = 9,8 кПа; R
2
= 0,987;
15,3
ˆ
F = 583;
α
F
< 10
-7
;
15
ˆ
t
= (14; 2,5);
t
α
ˆ
= (10
-7
; 0,025); S
0
τ
- среднеквадратичное отклонение (СО) остаточной ошибки ЭФР; R
2
- коэффициент
множественной детерминации;
21
, ff
F - статистика Фишера с числами степеней свободы f
1
= 3 и
f
2
= 15 (характеризует значимость всех коэффициентов регрессии);
2
ˆ
f
t - вектор статистик
Стьюдента с числами степеней свободы f
2
= 15 (характеризует значимость каждого
коэффициента);
F
α
ˆ
,
t
α
ˆ
- оценки уровней значимости величин
21
, ff
F и
2
ˆ
f
t
, найденные по
формулам работы [4]; значок ^ над символами означает «оценка»; векторы подчеркнуты.
Критический уровень значимости
α
к
= 0,05 выбран, согласно [4; Т2Р1], для „обычной
ответственности за вывод“ и предпочтительной альтернативной гипотезы. Значения элементов
вектора коэффициентов регрессии B = (b
0
b
1
b
2
)
т
зависят от размерности факторов. Если
размерность
τ
и
σ
- кг/см
2
,
γ
- г/см
3
, то В = (8,04; 0,462; -4,45)
т
; если
τ
и
σ
- кПа, а
γ
- кг/м
3
, то
В = (788; 4,62
⋅
10
-4
; - 439)
т
.
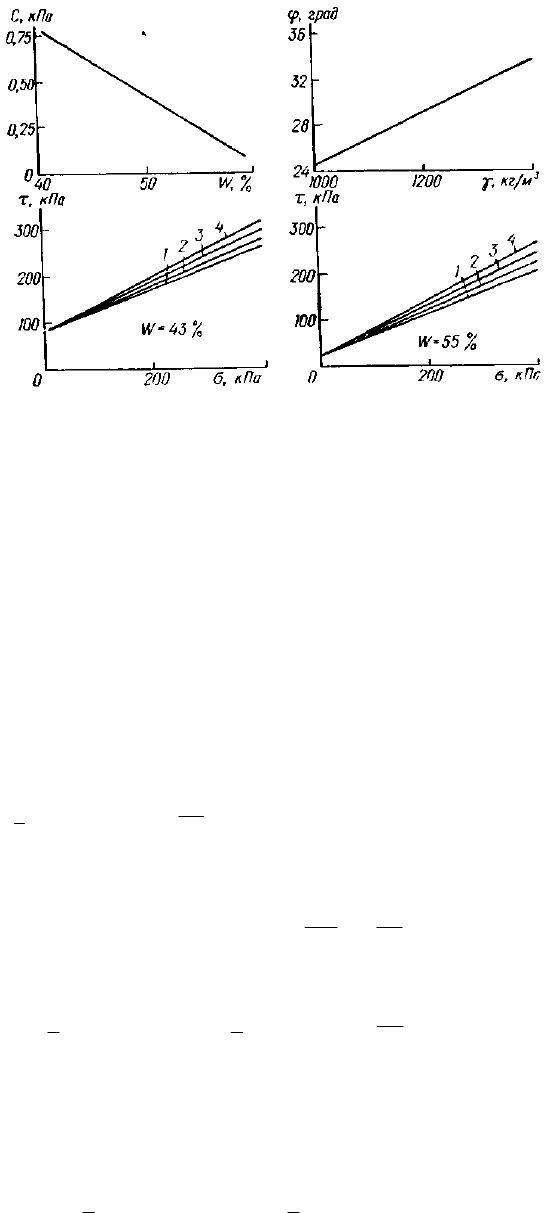
3
Рис 1. Связь основных переменных, характеризующих механические свойства шлама
дистилляции содового производства согласно эмпирической функции регрессии (3):
1 -
γ
= 1000 кг/м
3
; 2 – 1100; 3 – 1200; 4 – 1300.
Окаймим область E определения ЭФР (3). Из-за мультиколлинеальности факторов ЭФР
(3), область определения E окаймить сложно. Дело в том, что пространство факторов при
неоптимальном планировании экспериментов, как правило, не образует прямоугольную фигуру
(гиперпараллелепипед). Например, при корреляции двух факторов областью определения E может
быть эллипсом, сильно вытянутым вдоль случайно ориентированной главной оси. Задавая в
таком случае область E в виде прямоугольника, мы ошибемся, включив области, на самом
деле не принадлежащие E. Если же рассматривать вектор факторов как псевдослучайный,
нормально распределенный вектор, то область E допустимых значений этого вектора можно было
бы задать с использованием функции многомерного распределения. Однако эти уравнения
громоздки.
Предлагается задавать область определения E регрессионной модели с помощью системы
линейных неравенств.
Исходными данными являются выборочные моменты многомерного распределения вектора
факторов - средние
i
x , CO - S
i
(
к,1=i
) и коэффициенты корреляции r
ij
, 1
≤
i < j
≤
к.
Минимальные и максимальные значения факторов можно задать по усмотрению
экспериментатора, как минимальные и максимальные значения факторов, наблюдаемых в
эксперименте:
{
}
{
}
kiNjxxx
ij
j
iij
j
,1,,1,maxmin =∈<< (4)
или как нижнюю и верхнюю вероятностные границы области значений случайных факторов с
заданной надежностью (1 -
α
) по формулам
() ()
/2/2
;;1,,
iiiiii
kk
xxZSxxZSik
αα
−+
=−=+= (5)
где
−
i
x ,
+
i
x - нижняя и верхняя границы области допустимых значений случайных факторов x
i
в
пространстве R
к
; Z
α
/(2k)
- верхний
α
/(2к) - предел нормированного нормального распределения [4;
Ф(19)Р1]. Так, при (1 -
α
) = 0,94 и к = 3 по формуле [Ф(19)Р1] находим Z
α
/
δ
= Z
0,01
= 2,6.
Корреляционную связь между факторами можно учесть при описании области E с помощью
диагональной регрессии Фриша [5]
(
)
(
)
ˆ
sign/, 1
ijiijijjj
xxrSxxSijk
=+−≤<≤
, (6)
угловой коэффициент регрессии которой равен среднему геометрическому угловых
коэффициентов двух регрессий x
i
по x
j
и x
j
по х
i
; sign(r
ij
) - знаковая функция, sign(r
ij
) = -1 при r
ij
<
0; sign(r
ij
) = 1 при r
ij
> 0. Удобно считать, что sign r
ij
= 0 при r
ij
незначимо отличном от нуля, то есть
при |r
ij
| < r
α
/2
, где r
α
/2
- критическое значение коэффициента корреляции при заданном уровне
значимости
α
к
[4; Т2Р1].
4
Верхняя и нижняя «корреляционные» границы области Е образуются плоскостями,
проходящими параллельно диагональной регрессии Фриша (6). Эти плоскости, по усмотрению
экспериментатора, могут проходить через экспериментальные точки, максимально удаленные от
функции (6):
(
)
ˆ
max;
ijijijin
n
xxxx
−
=−−
%
(
)
ˆˆ
max;1,.
ijijinij
n
xxxxnN
+
=+−=
%
(7)
Можно также использовать нижнюю и верхнюю «вероятностные корреляционные» границы
(для этого необходимо учесть нижнюю и верхнюю толерантные границы, окаймляющие область
значений случайных ошибок регрессии) с заданной «надежностью» (1 -
α
):
()
(
)
()
(
)
22
/2/2
ˆˆˆˆ
1; 1; 1
ijijiijijijiij
kk
xxZSrxxZSzijk
αα
−+
=−⋅−=+⋅−≤≤≤
, (8)
где в (7) и (8)
+
ij
x
~
,
+
ij
x
ˆ
,
−
ij
x
~
,
−
ij
x
ˆ
- соответственно верхние и нижние «вероятностные
корреляционные» границы фактора x
i
, обусловленные корреляцией между факторами х
i
и x
j
.
В нашей задаче факторное пространство включает три фактора:
σ
, lgW,
γ
. Средние значения
факторов:
σ
= 228 кПа,
lg
W
= 1,686,
γ
= 1163 кг/м
3
; CO: S
σ
= 127, S
lgW
= 0,03, S
γ
= 63 кг/м
3
;
коэффициенты корреляции: r{
σ
, lgW} = -0,85; r{
σ
,
γ
} = 0,61; r{lgW,
γ
} = -0,88. Все коэффициенты
корреляции значимы с уровнями значимости
α
ˆ
= (5
⋅
10
-6
; 7
⋅
10
-3
; 10
-7
), определенными по методу
[4; Р3.7]. Используя соотношения (4), получим первую систему неравенств, задающих область E
определения регрессионной модели (3):
98 <
σ
< 392 кПа; 43 < W < 56%; 1050 <
γ
< 1810 кг/м
3
. (9)
Зададимся доверительной вероятностью (1 -
α
) = 95%. Рассчитаем «корреляционные»
границы области E по формулам (6) и (8). Для регрессии
σ
по lgW, согласно (6), получим
Wlg
ˆ
σ = 228 + (-1)
⋅
127
⋅
(lgW – 1,685)/0,03 = 7361 – 4233lgW;
согласно (8):
+
Wlg
ˆ
σ = 7361 – 4233lgW + 2,6
⋅
127(1 - 0,85
2
) = 7454 – 4233lgW;
−
Wlg
ˆ
σ = 7269 – 4233lgW.
Отсюда следует, что
7269 – 4233lgW <
σ
< 7454 – 4233lgW. (10)
Аналогично
1913 + 2,02
γ
<
σ
< 2329 + 2,02; 2,22 + 4,76
⋅
10
-4
γ
< lgW < 2,26 + 4,76
⋅
10
-4
. (11)
Область E, заключенная между границами (10), (11), не включает некоторые
экспериментальные точки (см. пунктир на рис. 2). Поэтому для ограничения области E решили
использовать соотношения (6) и (7):
7237 – 4233lgW <
σ
< 7489 – 4233lgW; 1953 + 2,02
γ
<
σ
< 2379 + 2,02;
2,06 + 4,76
⋅
10
-4
γ
< lgW < 2,26 + 4,76
⋅
10
-4
γ
. (12)
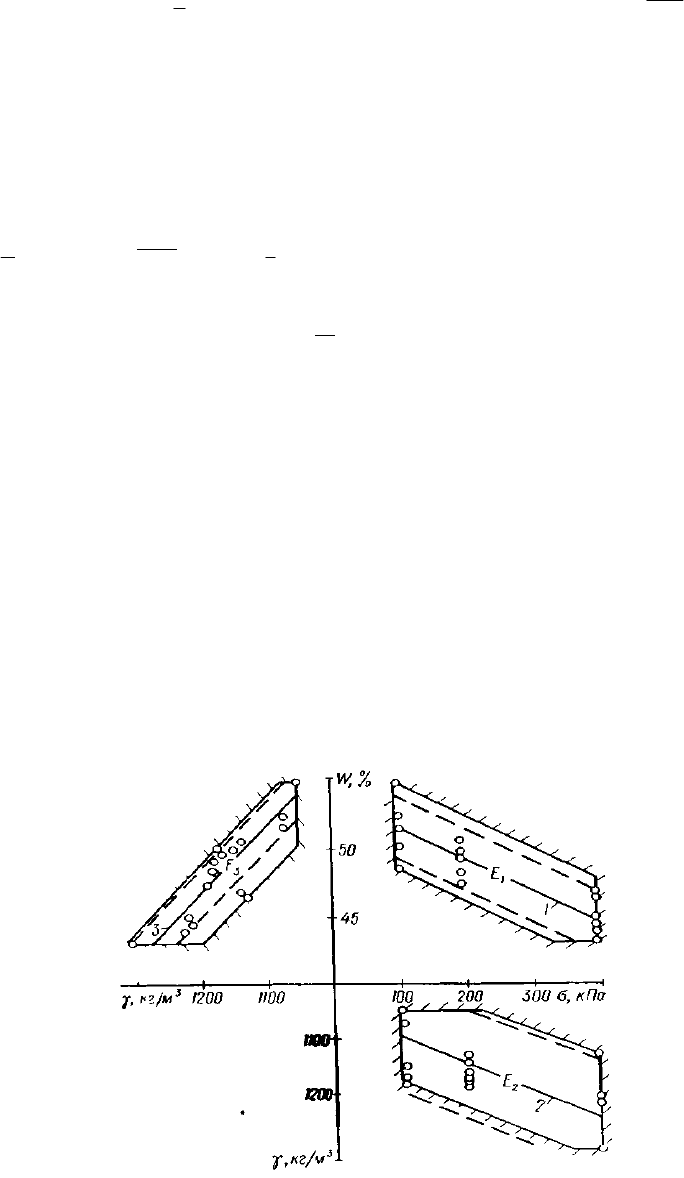
Рис. 2. Область E определения функции регрессии (3), описывающей зависимость сопротивления
шлама сдвигу, от различных факторов:
5
вертикальные и горизонтальные отштрихованные линии отображают систему неравенств (9), наклонные
штрих пунктирные - систему (10) (11), наклонные сплошные - (12) 1 – 3 - диагональные регрессии Фриша
(6).
Из выражений (9), (12) и рис. 2 видно, что область E определения модели (3), полученной по
данным «пассивного» эксперимента является довольно узкой.
Интерпретация модели (3) из-за мультиколлинеарности факторов не может быть
корректной. Модель (3) может быть использована лишь для аппроксимации экспериментальных
данных (см. табл. 1) на области E (см. рис. 2). Несмотря на ограниченное количество опытов и
неоптимальный план экспериментов, применение методов математической статистики при
исследовании механических свойств шлама дистилляции позволило выявить влияние влажности и
плотности сухого материала на основные расчетные характеристики - сопротивление материала
сдвигу, сцепление и угол внутреннего трения.
Замечание. Важно отметить, что область определения регрессионной модели
фиксируется на всём множестве факторов, характеризующих объект экспериментальных
исследований (см. введение): не варьируемых факторов (и, следовательно, не принятых в
расчёт) и варьируемых факторов, принятых в расчёт (а не только на подмножестве
значимых факторов, включённых в ЭФР)!
Литература
1. Маслов H. H. Основы механики грунтов и инженерной геологии.– M.: Высшая школа, 1968. - 630 с.
2. Гольдштейн M. H. Механические свойства грунтов. – M.: Стройиздат, 1973. - 376 с.
3. Девяткова Г. H. Программа пошаговой множественной регрессии с преобразованием исходной
матрицы. // В кн.: Регрессионные эксперименты (планирование и анализ). – M., 1977. – С. 212-230.
4. Колесникова С. В., Цейтлин H. A. α-метод проверки статистических гипотез в приложении к анализу
процесса приготовления суспензии гидроокиси кальция. -Хим. технология. -1982. -№ 6., С. 10-16.
5. Маленво Э. Статистические методы эконометрии. - M.: Статистика, 1975. - 424 с.
6. Заика А. М. Елисеев В. Н., Утешев B. М., Цейтлин Н. А. К вопросу о стабильности некоторых
показателей качества углекислотной белой сажи БС-120. В кн.: Минеральные наполнители. Труды
НИОХИМа, т. 54, Харьков, 1980, с.12-20.
7. Рудай А. Н., Цейтлин Н. А., Рудай В. И., Ицков Ф. Э. Разработка рациональных процедур программы
линейного регрессионного анализа. В кн.: Технология и автоматизация содового и смежных производств:
Труды, т. 61 / НИОХИМ. Харьков, 1985, с.72-84. [42]
8. Ицков Ф. Э., Рудай А. Н., Цейтлин Н. А. Алгоритмическое и программное обеспечение построения
регрессионных моделей химико-технологических процессов действующего производства. - Инф. бюлл. по
хим. пром. №1(122), 1989. - с.37-40. [56]
9. Цейтлин Н. А., Дружинина Т. Н., Юровский B. C., Чайка В. П. Решение основных проблем построения
регрессионных моделей экономических показателей химического производства. В кн.: применение
математических методов для интенсификации технологических процессов в производствах основной
химической промышленности: Тр. ХНПО "Карбонат". - Харьков, 1989.- т.68. -с.5-24. [55]
1
6.2.2. Оценка дисперсии воспроизводимости отклика в пассивном регрессионном
эксперименте и проверка гипотезы об адекватности регрессионной модели
Если воспроизвести эксперимент сложно, проведите его единожды. (Вредный совет)
В одноимённой работе [Цейтлин Н. А., Гордеев Д. С., Ицков Ф. Э., Рудай А. Н. - Теор.
основы хим. технологии, т. 21, №6, с. 830-835, 1987] предложена методика вычисления
смещённая (но вполне пригодной для практических нужд) оценки дисперсии ошибки
воспроизводимости отклика по данным пассивного регрессионного эксперимента. Эта оценка
позволяет приблизиться к решению задачи проверки гипотезы о не адекватности результатам
наблюдений эмпирической функции регрессии (ЭФР), построенной по данным пассивного
регрессионного эксперимента. Такая задача долгое время являлась камнем преткновения
статистической практики: любой исследователь, даже мало сведущий в тонкостях
регрессионного анализа, мог обоснованно усомниться в адекватности полученной регрессионной
модели.
Начнём с замечаний о некоторых терминах в регрессионном анализе. Одни авторы называют
остаточную дисперсию
2
ост
σ
«дисперсией адекватности» [1], другие – «дисперсией
неадекватности» [2], третьи, всё-таки по существу – «остаточной дисперсией» [9]. Мы
остановимся на этом термине. Величину дисперсии
2
в
σ
ошибки воспроизводимости отклика Y
одни авторы называют «ошибкой опыта» [1], другие – «ошибкой отклика» [2], третьи – «ошибкой
воспроизводимости случайной величины Y» [3]. Мы будем использовать более точный термин:
2
в
σ
- дисперсия ошибки воспроизводимости отклика, или кратко – дисперсия
воспроизводимости отклика (ДВО).
Одним из наиболее распространенных методов проверки адекватности ЭФР
экспериментальным данным [3, 4] является сравнение остаточной дисперсии
2
ост
σ с ДВО
2
в
σ
.
Проверяемая гипотеза имеет вид
2
в
2
ост0
: σσ =H ; (1)
альтернативная:
2
в
2
ост1
: σσ >H
(см. гипотезу № 17 [Т3Р1]). Если гипотеза (1) не отклоняется,
вычисляют средневзвешенную оценку дисперсии отклика [5; Ф(4)Р3.10], которую используют
затем для определения ряда статистических характеристик регрессионной модели.
Оценку
2
в
S дисперсии
2
в
σ принято получать с помощью параллельных опытов [1]. Однако в
пассивном эксперименте (например, при исследовании производственного процесса) возможность
проведения параллельных опытов, как правило, отсутствует. Поэтому в качестве оценки ДВО
принимают остаточную дисперсию ЭФР [2]. Очевидно, что такой подход корректен только в
случае, если структура ЭФР выбрана верно (например, из теоретических соображений). Таким
образом, не зная ДВО, нельзя проверить гипотезу (1) об адекватности ЭФР, не зная верной ЭФР,
нельзя оценить ДВО в пассивном эксперименте.
Чтобы разорвать этот «замкнутый круг», предлагается итерационная процедура построения
ЭФР с оцениванием ДВО. На первом этапе обычным пошаговым методом регрессионного анализа
[3] строится ЭФР
Y
ˆ
= f(b,x), (2)
где
Y
ˆ
- оценка отклика; b - оценка вектора
β
параметров ЭФР; х - n-мерный вектор факторов.
Вычисляется также оценка
2
ост
S остаточной дисперсии. Далее с помощью изложенной ниже
процедуры вычисляется оценка сверху
2
1
S
для ДВО. Сравнение оценок
2
ост
S
и
2
1
S
позволит
принять решение о неадекватности ЭФР либо об отсутствии оснований на данном этапе для
отклонения гипотезы об адекватности ЭФР.
Если первая ЭФР неадекватна, следует поменять структуру базисных функций и перейти ко
второму этапу - построить новую ЭФР и заново оценить ДВО. Процедуру следует продолжать,
пока не будет найдена структура ЭФР, обеспечивающая адекватную аппроксимацию данных.
Рассмотрим метод оценивания ДВО. Назовем опыты в точках х
i
и х
j
почти параллельными,
если выполняется условие
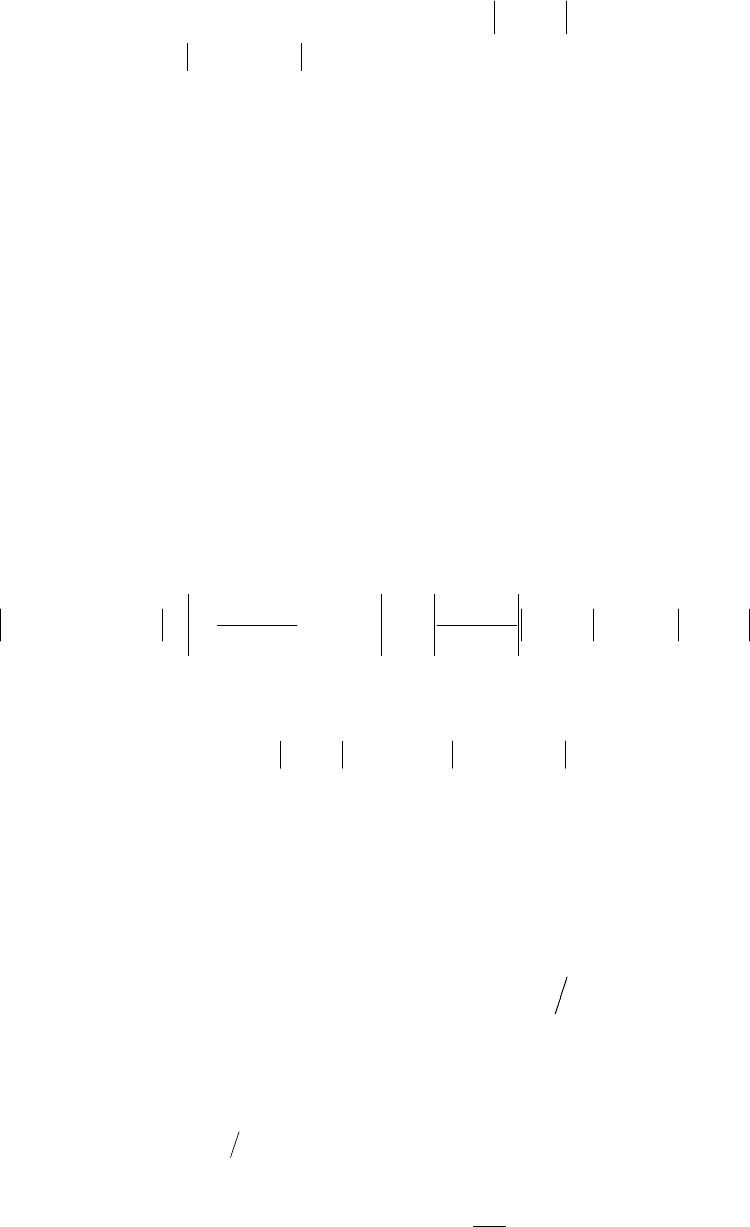
2
(
)
1
Фx,x
n
ijijrirjrK
r
DxxL
=
=−≤
∑
, (3)
где
[]
(
)
r
xx
ijr
xfD
ji
∂∂= /xb,max
;
; максимум берется по значениям х из отрезка с концами в
точках х
i
, x
j
∈
Ω
; x
r
- r-я координата вектора х;
Ω
- область действия. Величина L
K
выбирается
такой, чтобы условие (3) являлось достаточным для принятия гипотезы о равенстве значении
функции регрессии в точках х
i
и x
j
:
H
0
: f(
β
, x
i
) = f(
β
, x
j
) (4)
против альтернативы H
1
: f(β, x
i
) ≠ f(β, x
j
) (см. гипотезу № 1 [Т3Р1]).
При обычных предположениях регрессионного анализа [3] ЭФР f(b, х) имеет нормальное
распределение с математическим ожиданием f(β, х) и дисперсией
(
)
(
)
xfxf
T2
в
Cσ
, где
С - дисперсионная матрица; f(x) - вектор базисных функций (f(
β
, x) =
β
T
f(x)).
Для проверки гипотезы (4) воспользуемся статистикой
z = [f(b, х
i
) - f(b, х
j
)]/S
ij
, (5)
где S
ij
= S
в
[f
T
(х
i
)Cf(х
j
) + f
T
(х
j
)Сf(х
j
)]
0,5
, S
в
- оценка
σ
в
.
В нулевом приближении в качестве оценки σ
в
приходится принимать S
ост
- оценку, которая
может оказаться смещенной (завышенной); предпочтительной является гипотеза Н
0
(4) (см.
[Т2Р1]). Поэтому ужесточим критерий (5). Во-первых, заменим в (5) выражение f
T
(x
r
)Cf(x
r
) его
минимальным значением, равным N
-1
(N - количество наблюдений) [3]; во-вторых, полагая, что z ~
N(0; 1) и приняв критический уровень значимости α
к
= 0,05, получим критическое значение
верхнего (
α
к
/2)-предела: z
к
= l,96 [4]. Тогда гипотеза (4) не отклоняется в случае, если
|f(b,x
i
) – f(b,x
j
)| ≤ 1,96S
ост
(2/N)
0,5
= 2,8 S
ост
N
-0,5
= L
K
. (6)
Таким образом, достаточно показать, что |f(b,х
i
) - f(b,х
j
)|
≤
Ф(х
i
,х
j
).
Воспользовавшись формулой конечных приращений, имеем
()
()
(
)
()
(
)
()
∑∑∑
===
=−≤−
∂
∂
≤−
∂
∂
=−
n
r
n
r
jijririjrjrir
r
ij
n
r
jrir
r
ij
ji
xxDxx
x
f
xx
x
f
ff
111
x,xФ
xb,xb,
xb,xb, ,
где x
ij
- некоторая точка на отрезке [х
i
; х
j
]. На практике расчет всех nN(N - 1)/2 значений D
i,j,r
затруднителен, а использование размерной величины L
K
неудобно. Поэтому заменим функцию
Ф(а, с) безразмерной метрикой L(a, с):
()
1
1
a,c
n
Krrr
r
LLDac
−
=
=−
∑
;
(
)
r
x
r
xfD∂∂=
Ω∈
/xb,max
; a,c ∈ Ω. (7)
Неравенство Ф(х
i
, х
j
)
≤
L(х
i
, х
j
)L
K
, следующее из того, что D
ijr
≤
D
r
, еще более ужесточает
условие (3) «почти параллельности» опытов. Таким образом, на практике в качестве почти
параллельных опытов будем выбирать такие, чтобы
L(х
i
, х
j
)
≤
1. (8)
Заметим, что выполнение только одного условия (6) недостаточно для того, чтобы опыты в
точках х
i
и х
j
были почти параллельными, так как точки, удовлетворяющие этому условию, могут
лежать и на одной линии уровня ЭФР.
Искомую оценку ДВО находим но формуле
(
)
()
2
2
1
,
2
ij
ijI
SYYl
∈
=−
∑
, (9)
где I - множество пар индексов, соответствующих парам почти параллельных опытов; l -
количество элементов множества I; Y
i
, Y
j
- измеренные значения отклика в точках х
i
и х
j
.
Опишем некоторые свойства оценки
2
1
S
ДВО. Очевидно, что в случае, если пары значений
Y
i
и Y
j
соответствуют точно параллельным опытам (х
i
= х
j
) и встречаются в формуле (9) не более
одного раза, величина
2
в
2
1
σlS
имеет распределение «
χ
-квадрат» (
2
l
χ
) с l степенями свободы [6].
Оценим величину смещения оценки
2
1
S
в случае, когда справедлива гипотеза (4). Пусть для
принятой модели регрессии
Y
i
= f(β, x
i
) + ε
i
;
Ni ,1=
; ε
i
~ N(0;
2
в
σ
) (10)
выполняется условие cov(
ε
i
,
ε
j
) = 0 при i
≠
j. Тогда справедлива система равенств [7]:
{}
()
{
}
()
()
{
}
2
2
2
1
MM/2M,,/2
ijiijj
SYYlfxfxl
βεβε
=Σ−=Σ+−−=
