Цейтлин Н.А. Из опыта аналитического статистика

Подождите немного. Документ загружается.

()

{

}

{}{}

M,,MM/2

ijij

fxfxl

ββεε



=Σ−++=



(

)

(

)

222

вв

,,/2,

fxfxl

ββσσσ



=Σ−+=∆+



где М - оператор математического ожидания;

суммирование (

) ведется по парам индексов (i, j) ∈ I. Отсюда видно, что если х

– х

→ 0 для всех

(i, j)

∈

I, то M{

}

→

. Величина

∆σ

может быть оценена с помощью неравенства (6):

()

(

)

ост

b,xb,x/23,9

fflSN



∆=Σ−≤



. (11)

В соответствии с изложенным методом разработана программа «Дисперсия

воспроизводимости» (ДИВО), предназначенная для расчета на ЭВМ оценки ДВО отклика и

проверки гипотезы об адекватности ЭФР. В программе определяются пары опытов в порядке

возрастания расстояния L (7) между ними, оценки ДВО по накопленным парам опытов,

критерий [8, 9; Ф(51),(52)Р1] Фишера - Бонферрони (

) для проверки гипотезы об однородности

оценок усредняемых дисперсий,

-критерий Фишера (

) для проверки гипотез об

однородности оценок общей дисперсии отклика

общ

S и ДВО

, остаточной дисперсии

ост

S и

ДВО

S соответственно (см. гипотезу № 17 [Т3Р1]).

С помощью этих данных лицо, принимающее решение (ЛПР), оценивает ДВО и проверяет

гипотезу об адекватности ЭФР экспериментальным данным.

Лучшей смещенной оценкой ДВО

S является оценка, полученная на шаге с номером l,

если для всех r ≤ l выполнены условия

()

(

)

()()

1122

ˆˆ

x,x1;;,

ijKK

Lrrrαααα≤≥< (12)

где

1к

2к

- заданные критические уровни значимости (вообще говоря, разные) для

проверки соответствующих гипотез.

Гипотеза (1) об адекватности ЭФР не отклоняется, если для всех r

≤

Q, где Q – число пар

точек из N; Q = N(N-1)/2, выполняется наиболее важное условие

(

)

33,

αα

≥, или

(

)

{

}

33,

min,1,2,...,,

rrQ

αα≥∈

(13)

где α

3,к

- заданный критический уровень значимости.

Пример 1. Оценить ДВО по данным имитированного эксперимента. Задана модель

регрессии

()

(

)

0,5

2exp/2

Yxudu

πε

−

−∞

=+−+

∫

, (14)

где

~ N(0; 0,01). В качестве плана эксперимента (табл. 1) использована таблица равномерно

распределенных на отрезке [0; 1] случайных чисел x

и х

[4].

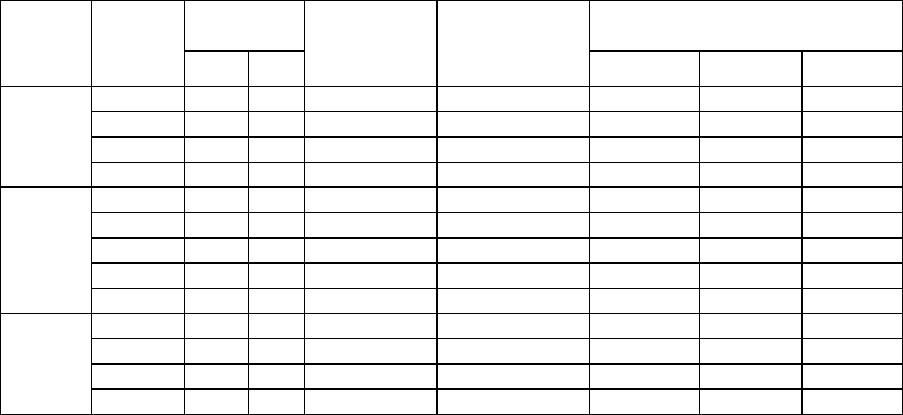
Таблица 1.

Имитация пассивного регрессионного эксперимента с помощью модели регрессии (14)

Факторы Факторы №

п/п

Ошиб-

ка ε

Функ.

М{Y}

От-

клик Y

№

п/п

Ошиб-

ка ε

Функ.

М{Y}

От-

клик Y

1 0,300

0,276

0,2455 0,6087 1,1543

11 0,916

0,361

0,1356 0,6410 1,6928

2 0,664

0,337

-0,0531

0,6319 1,2433

12 0,468

0,365

-0,0918 0,6424 1,0189

3 0,667

0,782

0,1279 0,7829 1,5775

13 0,904

0,937

0,0012 0,8257 1,7306

4 0,076

0,554

0,0046 0,7102 0,7904

14 0,923

0,431

-0,0911 0,6668 1,4991

5 0,111

0,352

-0,0525

0,6375 0,6957

15 0,538

0,110

0,1237 0,5442 1,2063

6 0,198

0,806

0,0007 0,7899 0,9887

16 0,038

0,917

-0,1384 0,8204 0,7202

7 0,194

0,049

-0,0162

0,5195 0,6969

17 0,331

0,161

-0,0959 0,5639 0,7994

8 0,193

0,544

-0,1618

0,7068 0,7382

18 0,889

0,434

0,0731 0,6678 1,6296

9 0,388

0,105

0,0378 0,5418 0,5796

19 0,995

0,981

0,072 0,9866 2,0526

10 0,449

0,174

-0,0057

0,5691 1,0124

20 0,967

0,362

-0,1633 0,6413 1,4449

Экспериментальные значения Y

отклика имитировали путем добавления значений ε

(i = l, ..., 20)

случайных нормально распределенных чисел [6] к значениям функции регрессии в точках x

Теперь «забудем» процедуру получения данных в табл. 1 и попытаемся получить

адекватную аппроксимацию этих данных. В основу структуры регрессионной функции возьмем

полином второго порядка двух переменных.

Обращение к программе пошагового регрессионного анализа [10] позволило выбрать

«наилучшее» уравнение регрессии без квадратичных членов

= 0,63 + 0,71x

+ 0,71x

(15)

со всеми значимыми коэффициентами и с минимальной остаточной дисперсией

ост

S = (0,15)

Оценим ДВО. С помощью программы ДИВО найдены две пары почти параллельных

опытов (табл. 2, расчет № 1).

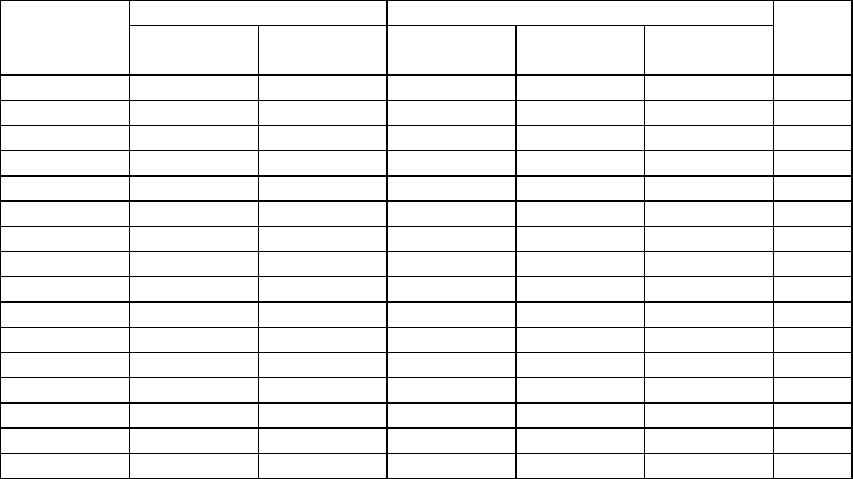
Таблица 2.

Результаты расчетов оценки дисперсии ошибки воспроизводимости отклика по программе ДИВО

Номера

строк

α-критерии однородности

дисперсий

№ ра-

счета

Номер

шага l

i j

Расстояние

L(l)(x

, x

)

СО ошибки

воспроизво-

димости S

(l)

(

)

(

)

(

)

1 14 18 0,54 0,090 - 0,2 0,45

2 11 20 0,76 0,140 0,55 0,1 0,60

3 4 8 1,85 0,120 0,36 0,03 0,44

4 10 17 1,96 0,130 0,76 0,02 0,46

1 5 13 0,41 0,145 - 0,02 0,16

2 1 9 0,72 0,114 0,43 <10

-3

0,03

3 4 12 0,74 0,093 0,25 <10

-4

0,003

4 3 11 0,78 0,157 0,23 <10

-5

0,005

5 2 10 1,52 0,410 0,02 <10

-4

0,10

1 5 13 1,20 0,145 - 0,02 0,37

2 4 12 2,10 0,103 0,31 <10

-3

0,10

3 1 9 2,20 0,093 0,25 <10

-4

0,04

4 3 11 2,30 0,157 0,23 <10

-5

0,10

Для увеличения мощности критерия адекватности, учитывая, что значения L(x

, х

) для

следующих двух пар незначительно превышают единицу, а также учитывая согласие α-критериев

Фишера и Фишера - Бонферрони с условиями (12), в качестве оценки ДВО возьмем оценку

(4) = (0,13)

«Правильность» расчета ДВО проверим с помощью нулевой гипотезы

: σσ =H (16)

против альтернативы

: σσ >H , где

{

}

MS=σ,

σ = 0,01 - заданная дисперсия случайной

величины

. Используем статистику Фишера

/σSF =

с числами степеней свободы f

= 4 и

= ∞. Получим оценку уровня значимости для проверки нулевой гипотезы (16):

= 0,14. Она

достаточно велика. Поэтому гипотезу (16) не отклонили.

Из данных расчета № 1 (табл. 2) видно, что условие (13) выполнено, значит, гипотеза об

адекватности ЭФР (15) не отклоняется.

Пример 2. Исследуется процесс очистки рассола (первая стадия), используемого в

производстве кальцинированной соды [11]. Одним из важных показателей процесса является

отношение массы жидкой фазы шлама к твердой. Требуется изучить зависимость этого показателя

от ряда факторов (табл. 3).

В предположении о линейности модели при планировании эксперимента был использован

дробный факторный план 2

5-2

с генерирующими соотношениями:

5413

xxxx

′

412

xxx

′

(где

′

кодированный фактор x

). Для оценивания ДВО и проверки адекватности ЭФР каждый опыт

предполагалось повторять дважды.

Таблица 3.

Экспериментальные данные по первой стадий очистки рассола

Расход реагентов, мл Концентрация эквивалента, НД*

Опыт

Сырой

рассол, х

Известковое

молоко, х

СаО в

молоке, х

рассоле, х

Ж/Т**,

1 750 65 106,8 5,03 5,20 11,16

2 650 68 66,40 5,00 5,10 8,490

3 745 42 67,00 2,94 4,90 5,070

4 660 41 107,0 3,10 4,95 9,820

5 755 40 65,80 4,92 2,98 2,880

6 650 41 105,3 5,05 3,05 10,99

7 760 66 106,6 3,00 2,90 21,75

8 640 63 68,10 2,92 2,88 20,10

9 753 65 107,3 5,10 5,18 11,26

10 647 68 66,80 4,93 5,14 9,720

11 742 42 67,60 2,88 4,87 5,450

12 663 41 106,4 3,15 4,98 9,800

13 757 40 65,40 4,90 3,00 3,090

14 652 43 105,9 5,02 3,08 12,13

15 757 65 106,1 3,50 2,78 20,66

16 645 62 67,60 2,94 2,91 19,35

*НД - нормальные деления. ** Ж/Т - отношение масс жидкой фазы шлама к твердой, кг/кг (Y).

При реализации плана эксперимента выдержать значения факторов в точности равными

планируемым не удалось (см. табл. 3). С помощью программы регрессионного анализа получили

ЭФР для отношения массы жидкой фазы шлама к твердой:

= 20,83 + 0,333x

- 2,69x

- 2,59x

+ 0,124x

– 0,024x

; (17)

все коэффициенты ЭФР значимы, оценка дисперсии остаточной ошибки

ост

S = (0,7)

Оценим ДВО. Строго говоря, в реализованном плане экспериментов параллельные опыты

отсутствуют. На практике исследователи иногда пренебрегают небольшим различием в значениях

факторов, связанным с отсутствием возможности в точности повторить условия эксперимента.

Результаты расчета по программе ДИВО помогут определить, в каких случаях это допустимо.

Зададимся критическими уровнями значимости (см. [Т2Р1])

3,к

= 0,01,

1к

2к

= 0,05. Из

расчета № 2 (табл. 2) видно, что почти параллельными оказались 4 пары опытов. На пятом шаге

первое и второе условия (12) не выполняются. В качестве оценки ДВО возьмем

(4) = (0,16)

Гипотеза об адекватности ЭФР (17) отклоняется, так как

(4) = 0,005 <

3к

. Поэтому перейдем к

следующему этапу.

Расширим список базисных функций, введя попарные произведения всех переменных,

включая новую базисную функцию x

/(х

+ x

), имеющую смысл соотношения объемов реагентов.

Повторное обращение к программе регрессионного анализа позволило получить ЭФР

= 254,13 – 238х

/(х

+ х

) - 2,74х

- 5,87х

/(х

+ х

) + 0,0333х

. (18)

Все коэффициенты ЭФР (18) имеют высокую статистическую значимость; оценка

остаточной дисперсии

ост

S = (0,31)

, что меньше соответствующей оценки для ЭФР (17) в 5 раз. В

предположении о том, что структура ЭФР (18) выбрана верно, почти параллельными нельзя

считать ни одну пару опытов (см. табл. 2, расчет № 3). Однако, поскольку в наибольшей степени

условиям (12) соответствует оценка ДВО

S (1) = (0,15)

(1) = 0,37 > α

3,к

, оснований для

отклонения гипотезы об адекватности ЭФР (18) данным эксперимента нет.

Литература

1. Новик Ф. С., Арсов Я. Б. Оптимизация процессов технологии металлов методами планирования

экспериментов. - M.: Машиностроение; София: Техника, 1980. - 304 с.

2. Вознесенский В. А. Статистические методы планирования эксперимента в технико-экономических

исследованиях. - 2-е изд. - M.: Финансы и статистика, 1981. - 263 с.

3. Себер Дж. Линейный регрессионный анализ. - М.: Мир, 1980 - 456 с.

4. Асатурян В. И. Теория планирования эксперимента. - М.: Радио и связь, 1983. - 296 с.

5. Химмельблау Д. Анализ процессов статистическими методами. -М.: Мир, 1973, 948 с.

6. Мюллер П., Нойман П., Шторм Р. Таблицы по математической статистике. - М.: Финансы и

статистика, 1982. - 272 с.

7. Закгейм А. Ю. Статистические оценки в некоторых химико-технологических задачах // Тр. МИТХТ

им. М. В. Ломоносова. – 1974. - Т. IV. - Вып. 2, - с. 3.

8. Колесникова С. В., Цейтлин Н. А. α-метод проверки статистических гипотез в приложении к анализу

процесса приготовления суспензии гидроокиси кальция // Хим. технология. - 1983. - № 1. - С. 47.

9. Афифи А., Эйзен С. Статистический анализ: Подход с применением ЭВМ. - М.: Мир, 1982. - 488с.

10. Петрович М. Л. Регрессионный анализ и его математическое обеспечение на ЕС ЭВМ. - М.:

Финансы и статистика, 1982. - 200 с.

11. Фурман А. А., Шрайбман С. С. Приготовление и очистка рассола. - М.: Химия, 1966.

6.2.3. Представление корреляционной матрицы в упрощённой записи.

Чтобы преодолевать препятствия, совсем не обязательно всегда их тщательно изучать,

иногда достаточно просто не обращать на них внимания. Стас Янковский

Однажды на консультацию к автору пришел молодой аспирант Александр Савчук с

толстой папкой выписок из историй болезней. Каждая такая «история» включала около 150-ти

численных значений медицинских параметров. Врач попросил рассчитать «по стандартной

программе ППП» «корреляционную матрицу» (КМ) |r

| размерностью 150*150. Кроме КМ

«стандартная программа» приводит соответствующие «матрицу уровней значимости» (МУЗ)

|α

| и «матрицу объёмов не пропущенных пар элементов исходной выборки» (МОН) |N

| такой

же размерности. Каждый элемент r

КМ и соответствующий элемент α

занимали по 9 позиций

(с пробелами!), причём последние цифры в этих не округлённых числах были явно незначащими.

Элементы N

МОН занимали по 4 позиции (например, r

75;124

= -0,16097; α

75;124

= 0,04928;

75;124

= 151). Распечатка этих матриц заняла несколько метров бумаги. Изучение и анализ КМ

заключались в поиске значимо отличных от нуля элементов КМ, их сравнении между собой и

правдоподобной содержательной интерпретации. Мало того, что такая КМ, занимающая

292500 позиций, была необозримой, трудоемкой при переписывании и представлении в научном

отчете, в ней порядка 80% коэффициентов корреляции оказались незначимыми, то есть

напрасно мелькали перед глазами! Для облегчения жизни молодых аспирантов пришлось

разработать очередную рациональную процедуру корреляционного анализа, позволяющую

редуцировать (сократить) эти матрицы до обозримых размеров без потери точности и

пригодности для изучения. Так появилась компьютерная подпрограмма «редукция

корреляционной матрицы» (см. раздел 6.2.6). Эту процедуру мы сделали с программистом

Анатолием Николаевичем Рудаём и описали в одноименной работе (Дубницкий В. Ю.,

Цейтлин Н. А. - В кн.: Системы обработки информации: Труды, вып. 1 (5), НАНУ, ПАНИ, ХВУ. -

Харьков, 1999, с. 6-9.).

Максимального сокращения записи КМ с сохранением достаточной для практики точности

ее элементов и возможности одновременной проверки их значимости можно добиться так.

Отрезок (-1, 1) области значений элементов r

КМ необходимо разделить на ряд интервалов

статистической неразличимости (СН). Значения r

, попадающие в соответствующий интервал,

считать равными «принятому значению» ρ

пi

и закодировать цифрой, буквой или другим символом,

используемым на АЦПУ ЭВМ. Коды значений r

расположить над главной диагональю КМ,

соответствующие знаки g

= sgn(r

) - под ней (здесь sgn(·) – знаковая функция; g

= sgn(r

) = «+»,

если r

> 0 и g

= sgn(r

) = «-», если r

< 0).

Для расчета границ указанных интервалов используются положения теории проверки

статистических гипотез [1]. Первый интервал СН (-ρ

, ρ

) в окрестности нуля рассчитывается на

основании статистического критерия проверки гипотезы о том, что коэффициент корреляции

= 0

против альтернативы ρ ≠ 0 на уровне значимости α

. Границы -ρ

и ρ

первого интервала СН

являются верхней и нижней границами второго и третьего интервалов (-ρ

,- ρ

] и [ρ

, ρ

характеризующих неразличимость оценок r

, попадающих в эти интервалы на уровне значимости

. Аналогично строятся следующие интервалы СН.

Учитывая симметрию относительно нуля распределений двух оценок коэффициентов

корреляции -r и r с математическими ожиданиями -ρ и ρ, равными по абсолютной величине,

будем рассматривать только половину (0, 1) области значений величины ρ. На области (0, 1)

строятся интервалы СН (0,

), [

), …, [

, 1).

Распределение выборочной оценки r коэффициента корреляции ρ, когда ρ ≠ 0 асимметрично

относительно математического ожидания так, что при одинаковых уровнях значимости α

каждый

следующий интервал СН [ρ

, ρ

i+1

) у'же предыдущего [ρ

i-1

,ρ

)

(

)

2,1

=−

. При большом числе N

опытов, по которым рассчитываются оценки r

из КМ, таких интервалов может оказаться слишком

много, что неудобно для анализа. Для уменьшения числа интервалов используются два приема.

1) Задается верхний предел

дробления отрезка (0, 1) интервалами так, что интервал [

п-1

), накрывающий значение

, является предпоследним; последним является интервал [

, 1).

Рекомендуется принимать величину ρ

= 0,999.

2) Первый интервал СН (0, ρ

) строится на «обычном» уровне значимости α

(например, α

0,05), а предпоследний интервал [

п-1

) – на очень малом уровне значимости

(например,

0,001). Промежуточные интервалы строятся на уровнях значимости α

∈ (α

, α

), которые

предлагается определять по формуле

()

; 2,

ρρ

αααα

−

. (1)

Интервалы СН строят с помощью следующих преобразований. Используются

аппроксимация Сливняка для верхнего α/2–предела u

нормированного нормального

распределения величины U ~ N(0, 1) (с центром в нуле и дисперсией 1) [1]:

= 1,94(-lg(α(2 - α)))

0,5

; u

∈ U (2)

и аппроксимация Рокицкого для верхнего

/2–предела t

f,α/2

(f = N – 1) распределения

Стьюдента t

с f степенями свободы [1]:

= u

(1 + u

/(N+ 1 – 1,5 u

)). (3)

При большом числе опытов (N > 9) используется преобразование из нормального

распределения [2]

(

)

(

)

iiii

ZZZZ

iii

thZeeeeZR

−−

==−+∈

, (4)

где

(

)

iiZ

νσ

с центром

и дисперсией

;

, причем

= (N -3)

-0,5

; (5)

при малом числе опытов (4 ≤ N ≤ 9) – из распределения Стьюдента [2]

(

)

0,5

iii

ttNρ=+− . (6)

Определим границы

(

=) интервалов СН для абсолютных величин коэффициентов

корреляции |r

| на области (0, 1). Пусть N > 9. Найдем верхнюю границу

первого интервала СН

(0, ρ

). Для проверки гипотезы ρ = 0 против альтернативы ρ ≠ 0 используется статистика [2, с. 395]

. Заменив статистику

критическим значением

и выразив

через N, получим

значение

()

0,5

1/2

3ZuN

−

=−, (7)

которое по формуле (4) приводит к границе ρ

Границы ρ

второго и следующих интервалов СН (ρ

i-1

,ρ

] (

) строим, исходя из

гипотезы ρ

= ρ

i-1

против альтернативы ρ

≠ ρ

i-1

. Определив по формуле (1) критическое значение

уровня значимости α

, используем выражение для критерия значимости [2, с. 396]

()

(

)

/21

iiZ

uZZ

−

=− , откуда

()

(

)

0,5

1/2

2/3;2,

ZZuNin

α−

=+−= (8)

и по формуле (5) - ρ

Для расчета принятых внутри интервалов СН (ρ

i-1

,ρ

] значений ρ

пi

(

) коэффициентов

корреляции берутся середины интервалов (Z

i-1

, Z

]: Z

пi

= (Z

i-1

+ Z

)/2, а затем по формуле (4)

определяют

пi

= thZ

пi

(значение

п1

= 0).

При малых N (4 ≤ N ≤ 9) для построения границ ρ

интервалов СН используется

распределение Стьюдента.

Значение ρ

вычисляется по формуле (6), где величина t

определяется при заданном α

по

формулам (2) и (3). Следующие границы ρ

определяются по формуле (6), где

1,/2

2;2,

iif

tttin

α−

=+=

; (9)

значение α

вычисляется по формуле (1);

,/2

- по формулам (2) и (3).

Принятые значения ρ

пi

(

) определяют по формуле (6), где вместо t

используется

полусумма (t

i-1

+ t

)/2, а ρ

п1

= 0.

Описанный алгоритм лег в основу подпрограммы РЕКОР (РЕдукция КОРреляционной

матрицы), которая была включена в пакет программ регрессионного анализа РЕГАН [3].

Возможности подпрограммы РЕКОР иллюстрируются распечаткой большой КМ

размерностью 44

44 (таблица).

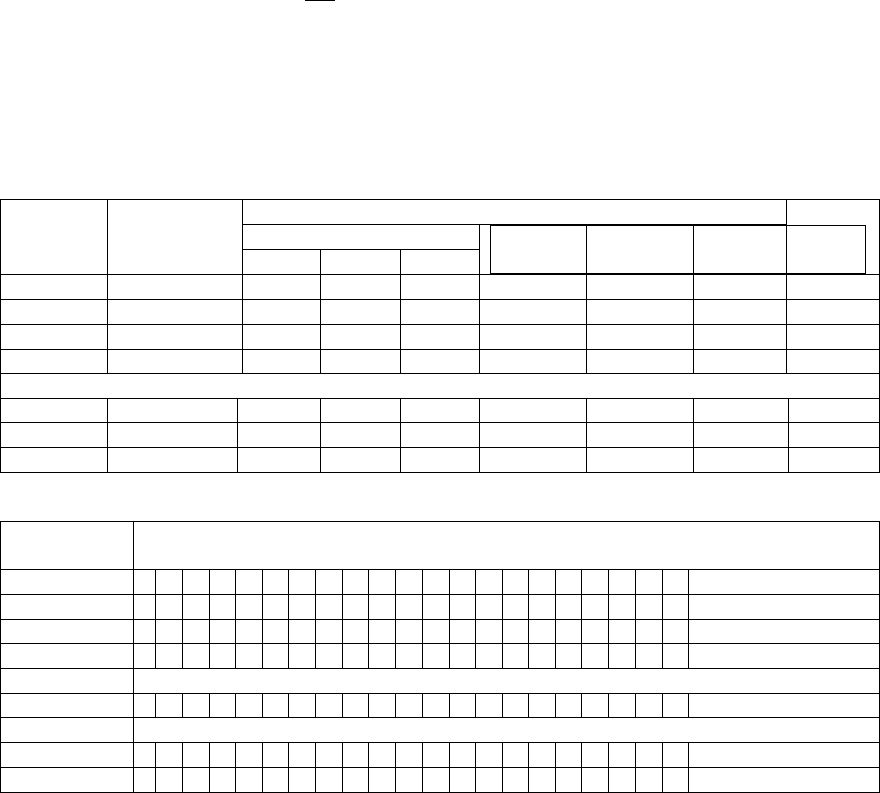
Таблица

Фрагменты изображения корреляционной матрицы на мониторе РС, или распечатки на АЦПУ.

Коэффициенты парных корреляций

Частота для g

∈

(-; 0; +)

Номер i

интер-

вала СН

Символ

кодирования

(-) (0) (+)

Нижний

уровень

Принятое

значение

Верхний

уровень

Уровень

значимо-

сти α

0 0 - 2 - 0 0 (точно) 0 -

1 1 - 136 - 0 0 0.20 0.05

2 2 167 - 84 0.20 0.33 0.45 0.023

3 3 60 - 135 0.45 0.58 0.69 0.0086

и так далее

10 а 3 - 3 0.9983 0.9989 0.99932 0.001003

11 в 0 - 7 0.99932 0.99957 1 0.001

12 с 1 - 45 1 1 (точно) 1 -

Корреляционная матрица в символах:

Переменная

над главной диагональю – символы принятых значений;

«*» - пропущенное значение; под главной диагональю – матрица знаков

Десятки →

Единицы → 12

1 с2

2 -

и так далее и так далее

27 +-

+ -

- +

- -

+ -

- +

- -

+ -

- +

с2

1с

в1

и так далее и так далее

43 - -

- +

- -

+ -

- +

+ -

- +

- -

+ -

- +

с4

44 -+

+ -

- +

- -

+ -

- +

+ -

- +

+ -

- +

+с

В нулевом интервале СН оказалось два значения r

, точно равных нулю и 136 значений,

статистически не отличающиеся от нуля; не значимые на уровне значимости 0,05 коэффициенты

корреляции r

и попадающие в интервал СН (-0,2; 0,2) закодированы единицами. Двойками

закодированы 167 отрицательных и 84 положительных значений r

, абсолютные значения которых

накрываются интервалом (0.20; 0,45] и статистически не различимы на уровне значимости 0,023 от

принятого значения 0.33; значений r

, равных -1 и 1 оказалось 1 и 45, соответственно.

Приведем расшифровку некоторых элементов r

КМ: r

1;1

= 1 (точно; символ «с»); r

1;2

= -0,33

(см. символы «-» и «2»); r

1;3

= 0 (точно; символ «0»); r

1;4

= 0,58 (символ «3»); r

1;44

пропущен

(символ «*»); r

27;30

= 1 (точно; символ «с»); r

27;33

= 0,99957 (символ «в»).

Литература

1. Цейтлин Н. А. Применение методов математической теории эксперимента в содовой промышленности.

Обзорная информация. Серия «Содовая промышленность». – М.: НИИТЭХИМ, 1984. – 36 с.

2. Закс Л. Статистическое оценивание. – М.: Статистика, 1976. – 598 с.

3. Рудай А. Н., Цейтлин Н. А., Рудай В. И., Ицков Ф. Э. Разработка рациональных процедур программы

линейного регрессионного анализа // В кн.: Статистические методы в основной химии: Труды. – Т. 63. –

Харьков: НИОХИМ, 1986. С. 72 – 84.

6.2.4. Построение интерпретируемой регрессионной модели технологического объекта

С тех пор как за теорию относительности принялись математики,

я ее уже сам больше не понимаю. (А. Эйнштейн)

Всякую интерпретацию можно рассматривать как процесс обработки данных

эксперимента с целью получения информации об интересующем объекте [1, с. 9]. В

регрессионном анализе под интерпретацией модели регрессии часто подразумевается анализ

зависимости отклика (точнее, его математического ожидания) от каждого из факторов в

отдельности [2, с. 191]. Такой анализ позволяет лучше понять физико-химические основы

процесса, найти способы управления им. Решение задач регрессионного анализа возможно

осуществить с помощью эмпирической функции регрессии, адекватной экспериментальным

данным [3, с. 86], корреляция оценок параметров в которой статистически незначима [4, с. 82].

В основе теории регрессионного анализа лежат предположения о нормальном распределении

независимых остатков функции регрессии с постоянной дисперсией [4, с. 138]. Для выполнения

этих предположений необходимо, чтобы структура фикции регрессии f(

, x) была выбрана

правильно, т. е.

MY = f(

, x), (1)

где MY - математическое ожидание отклика Y,

- вектор параметров функции рецессии f (

⋅

подлежащий оценке, х - вектор факторов.

При моделировании технологических показателей структура правильной функции

регрессии обычно неизвестна. При использовании эмпирических полиномиальных моделей

необходимое условие (1) выполнения основных предположений нарушается. Тем не менее, в

активном эксперименте, осуществленном по ортогональному плану [2, 3], получают

независимые оценки параметров

, и серьезные проблемы интерпретации не возникают [2].

Более сложной является задача обработки результатов пассивного эксперимента, когда нет

возможности получить независимые оценки параметров. Найденные модели можно

использовать только для аппроксимации данных на специальным образом окаймлённой

области определения регрессионной модели (см. раздел 6.2.1). В одноимённой работе

(Ицков Ф. Э., Рудай А. Н., Цейтлин Н. А. - В кн.: Применение математических методов для

интенсификации технологических процессов в производствах основной химической

промышленности: Тр. НХПО "Карбонат". - Харьков, 1989 - т.68. - с.40-47.) предлагается

эвристическая процедура построения линейных

регрессионных моделей со статистически

незначимой корреляцией оценок коэффициентов по данным пассивных наблюдений. В основе

процедуры лежит идея выбора из множества пассивных данных такого подмножества, которое

доставляло бы минимум максимальному по модулю коэффициенту корреляции оценок

коэффициентов регрессии.

В случае, если бы выполнялись основные предположения регрессионного анализа, удаление

элементов выборки неизбежно привело бы к увеличению дисперсии оценки функции отклика,

уменьшению мощности статистических критериев, потере части информации об объекте,

сужению области определения модели.

Эмпирическая же функция регрессии, построенная на меньшей области, может иметь

лучшие статистические характеристики. Это связано как с лучшими аппроксимирующими

свойствами функции регрессии выбранной структуры на меньшей области, так и лучшей

обусловленностью матрицы плана. Отброшенные точки определяют оставшуюся часть

области. Такая область может оказаться параллелепипедом или эллипсоидом, или шаром,

встроенном в изученную область.

В результате предложенного подхода могут быть получены как минимум – две

регрессионные модели: одна – для аппроксимации данных на всей изученной и специальным

образом окаймлённой области определения модели, и вторая модель, определённая на части

изученной области – для интерпретации.

Математическая постановка задачи. Пусть X - исходная матрица пассивных наблюдений

факторов размерности N

m, Y - вектор наблюдений отклика размерности N. (Будем считать, что Х

- расширенная матрица, то есть, содержащая не только столбцы факторов, но и столбцы

преобразований). Тогда, согласно методу наименьших квадратов,

вектор b оценок коэффициентов

регрессии определяется из уравнения [3]

X`Xb = XY. (2)

Матрица (Х'X)

-1

представляет собой ковариационную матрицу вектора b (

- дисперсия

воспроизводимости отклика).

Установим связь между матрицами корреляции коэффициентов и факторов.

В методе наименьших квадратов часто применяется центрирование и нормирование

факторов. Иными словами, формируется

матрица

, столбцами которой являются векторы [4]

()

iiii

XXXXX −−=/

, (3)

где X

- i-й столбец матрицы X;

X - столбец с компонентами, равными среднему значению

компонент вектора x

; норма евклидова. Затем решается система уравнений

YXaXX

ooo

′

(4)

относительно вектора a. Искомые коэффициенты регрессии определяются по формуле

(

)

mixxab

iiii

,...,1,/ =−=

. (5)

Заметим, что

′

- матрица выборочных корреляций факторов,

)(

−

′

- матрица

выборочных корреляций вектора коэффициентов a

. Так как коэффициенты b

отличаются от

коэффициентов a

постоянными множителями (cм. (5)), то корреляционные матрицы векторов a и

b совпадают.

Теперь установим связь между свойством «почти диагональности» для матриц корреляции

факторов и коэффициентов.

Пусть А - квадратная матрица с единицами на диагонали и с числами по модулю, меньшими

единицы, вне диагонали. Представим ее в виде А = I + B, где I - единичная матрица. В качестве

нормы матрицы примем [4]

mji

≤≤

max

. (6)

По условию, ||B|| < 1, значит, справедливо разложение в ряд Неймана [4]

-1

= (I + B)

-1

= I – B + B

- … = I + P (7)

и неравенство для норм

||P|| = ||(I + B)

-1

– I||

≤

||B||/(1 - ||B||). (8)

Из неравенства видно, что если ||B||

→

0, то ||P||

→

0. Отсюда следует важный вывод:

процедура диагонализации матрицы A влечет за собой диагонализацию матрицы А

-1

Применительно к нашей задаче, если положим A =

′

, ортогонализация столбцов

матрицы плана эксперимента влечет за собой ортогонализацию оценок коэффициентов регрессии.

Верно и обратное утверждение.

Таким образом, условия малости по модулю вне диагональных элементов для

корреляционных матриц факторов и оценок коэффициентов регрессии выполняются

одновременно.

Как видно из неравенства (8), для того, чтобы корреляции коэффициентов регрессии не

превышали некоторого критического значения (||P|| < r

), достаточно, чтобы выполнялось

неравенство для корреляций переменных

||B|| < r

/(1 + r

) = r

. (9)

На основании этих выводов можно проводить диагонализацию матрицы корреляции

коэффициентов регрессии с помощью ортогонализации столбцов матрицы плана Х. Это в

значительной степени сократит объем вычислений.

Рассмотрим

алгоритм поочередного исключения строк.

Пусть количество уже исключенных из матрицы X строк равно (L – 1) и в результате

получена матрица X(L - 1). Тогда нa L-м шаге в цикле по k от 1 до (N – L + 1) выполняют

следующие четыре операции.

1. Из матрицы X(L - 1) исключают k-ю строку. В результате получают матрицу X(L, k).

2. С использованием формулы (2) центрируют и нормируют матрицу X(L, k). В результате

получают матрицу

()

kLX

3. Вычисляют матрицу

()

kLX

′

()

kLX

и ее определитель D

4. Если D

≠

0, определяют

()()

1,, −⋅

′

= kLXkLXr

, т.е. максимальный по модулю

внедиагональный элемент корреляции факторов. Если D

= 0,то r

остается неопределенной

величиной.

По выходе из цикла производят дальнейшие операции.

5. Если D

= 0 (k = 1, …, N - L), то в качестве ответа представляют матрицу X(L – 1) и

значение r

L - 1

(см. п. 6 и 7).

6. Если не все определители нулевые, то устанавливают такое значение k, при котором

= min r

; причем j принимает такие значения, что D

≠

0; 1

≤

N – L.

7. Осуществляют присвоения: X(L) = X(L, k), r

= r

L, k

8. Проводят сравнение

< r

= r

/(1 + r

), (10)

где r

- критическое значение коэффициента корреляции, которое зависит от принятого

критического уровня значимости

для проверки гипотезы Н

: ||P|| = 0 против альтернативы H

||P|| > 0, от размерности задачи т, а также числа степеней свободы, равного L. Например, eсли

= 0,2, т = 3, L = 50, вычисляем [4, с. 223]

= 1 – (1 -

)

, (11)

где р =

C = 3;

= 0,08. Из таблицы [5, с. 248] определяем r

= 0,25.

Если условие (10) выполняется, то гипотеза H

не отклоняется. Расчет считается

выполненным успешно. В ответе распечатывают матрицу Х(L) и значение r

9. Если условие (10) не выполняется, то присваивают L = L + I и производят возврат к п. 1

для выполнения следующего шага.

Предложенный алгоритм имеет следующие недостатки: он требует большого числа

вычислений (на L -м шаге вычисляется N – L матриц корреляции); он не является алгоритмом

полного перебора (так как удалять строки можно по две, три и больше) и, значит, не обеспечивает

решения задачи в случае его существования.

Очевидно, что алгоритм полного перебора, требующий большого объема вычислений, тем

труднее применить на практике, чем больше объём выборки. Поэтому рассмотрим метод

исключения "далеких" точек, позволяющий изъять строки, которые содержат "большие"

координаты, приводящие к корреляции соответствующих столбцов.

Обозначим К-орт, соответствующий k-й строке матрицы X;

X ,

X - нормированные,

центрированные столбцы матрицы Х. Запишем неравенства треугольников для троек векторов

KXKXKXKXX

,,X- ;,,X- ;,,X ;,,

iii

−− :

;;

oooooooo

ijijijij

oooooooo

ijijijij

XKXKXXXKXKXX



−+−≥−−+−−≥+







−−+−≥−−−−+−−≥−+





(12)

выразим их через скалярные произведения

1,1,1,;1,1,1,;

1,1,1,;1,1,1,

oooooooo

ijijijij

oooooooo

ijijijij

XKXKXXXKXKXX





−+−≥−−++≥+















++−≥++++≥−









(13)

Из выражений (13) следует