Цейтлин Н.А. Из опыта аналитического статистика
Подождите немного. Документ загружается.

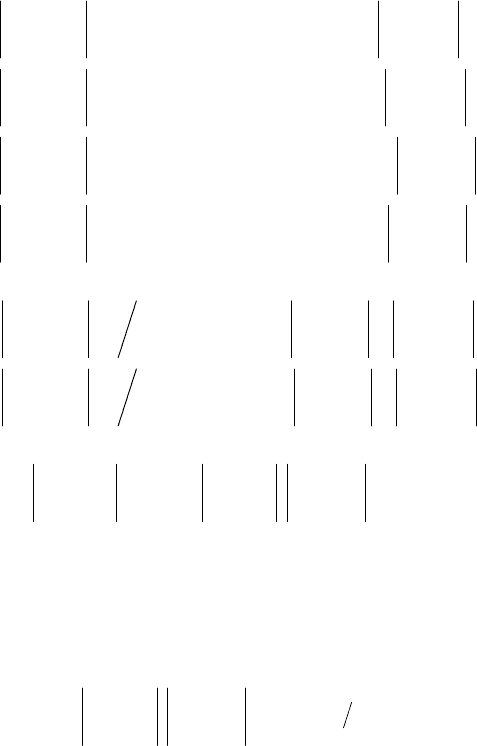
4
o
i
,4,3 npu X,,
oooo
ijij
XXXKKXK
≥−≤
; (14.1)
i
,4,3 npu X,,
ooooo
ijjj
XXXKKXK
≥−≥
; (14.2)
o
i
,4,3 npu X,,
oooo
ijij
XXXKKXK
−≥−≤−
; (14.3)
i
,4,3 npu X,,
ooooo
ijjj
XXXKKXK
−≥−−≥−
; (14.4)
i
,4,3 npu X,,
ooooo
ijjj
XXXKKXK
−≥−≤−
; (14.5)
i
,4,3 npu X,,
ooooo
ijij
XXXKKXK
−≥−−≥−
; (14.6)
i
,4,3 npu X,,
ooooo
ijjj
XXXKKXK
≥−−≤
; (14.7)
i
,4,3 npu X,,
ooooo
ijij
XXXKKXK
≥−−≥
. (14.8)
Объединив пары неравенств (14.1) и (14.3); (14.6) и (14.8); (14.2) и (14.5); (14.4) и (14.7), получим
i
i
j
,4,3 npu X,,;
,4,3 npu X,,;
,4,3 npu X,,;
,4,
ooooo
ijij
ooooo
ijij
ooooo
ijji
ooo
ijj
XXXKKXK
XXXKKXK
XXXKKXK
XXXK
≥−≤
≥−−≥
≥−≤−
≥−
o
j
3 npu X,,.
o
i
KXK
−≥
(15)
Объединим теперь первые и последние два неравенства (15):
i
i
,4,3 npu X,,;
,4,3 npu X,,.
ooooo
ijij
ooooo
ijjj
XXXKKXK
XXXKKXK
≥−≥
≥−≤
(16)
Из последних двух неравенств следует
3,,,min4, −
≥
KXKXXX
o
j
o
i
o
j
o
i
. (17)
Для того, чтобы выборочная корреляция
=
o
j
o
iij
XXr ,
векторов
o
i
X ,
o
j
X была по модулю
больше критического значения r
**
, достаточно, чтобы их k-е координаты
KX
o
i
,
,
KX
o
j
,
удовлетворяли условию
()
rrKXKX
o
j
o
i
′
=+≥
43,,,min
*
. (18)
Таким образом, из рассмотрения предлагается исключить такие строки, которые после
нормировки столбцов содержат хотя бы две компоненты, превышающие значение r'. Метод
исключения "далеких" точек используется перед включением алгоритма поочередного удаления

5
строк и позволяет изъять строки, которые заведомо приводят к мультиколлинеарности столбцов
матрицы Х.
По изложенным алгоритмам составлена программа INTER для ЭВМ ЕС.
Приведем результаты расчета контрольного примера. В качестве исходных данных была
взята матрица плана для двух переменных X
1
, Х
2
полного факторного эксперимента 2
2
и точек,
расположенных вдоль прямой X
1
= Х
2
. Критический уровень значимости для проверки гипотезы о
не значимости коэффициента корреляции принят равным 0,01. В результате расчета отброшено
девять точек (см. таблицу).
Таблица
Ортогонализация плана эксперимента по программе INTER в контрольном примере
Номер точки 1 2 3 4 5 6 7 8 9 10 11 12 13 14
Шаг* - - - - - 9 8 7 6 5 4 3 2 1
Переменные Х
1
1 1 -1 -1 2 -3 4 -5 6 10 -17 18 -19 40
Х
2
1 -1 1 -1 2 -3 4 -5 6 10 -17 18 -19 40
*Шаг, на котором была отброшена точка.
Выборочный коэффициент корреляции факторов Х
1
, X
2
, рассчитанный по оставшимся пяти
точкам, равен 0,444. Следовательно, значение выборочного коэффициента корреляции коэффи-
циентов регрессии меньше 0,8 (критическое значение коэффициента корреляции при
α
k
= 0,01 и
числе степеней свободы f = 4 равно 0,8). Пример фактического использования программы INTER
приведен в работе [6].
Литература
1. Гольцман Ф.М. Статистические модели
интерпретации. – М.: Наука, I971. - 328 с.
2. Адлер Ю. П., Маркова E. В., Грановский Ю. В. Планирование эксперимента при поиске оптимальных
условий. - M.: Наука, 1976. – 80 с.
3. Асатурян В. И. Теория планирования эксперимента: Учеб. пособие для вузов. - M.: Радио и связь, 1983.
- 248 с.
4. Себер Дж. Линейный регрессионный анализ. - M.: Мир, 1980. - 456 с.
5. Большев Л. H., Смирнов Н. В. Таблицы математической статистки. - M.: Наука, 1983. - 416 с.
6. Цейтлин H. А. и др. Решение основных проблем построения регрессионных моделей экономических
показателей химического производства // - В кн.: Применение математических методов для интенсификации
технологических процессов в производствах основной химической промышленности: Тр. НХПО
"Карбонат". - Харьков, 1989 - т.68. - с. 5 - 24.
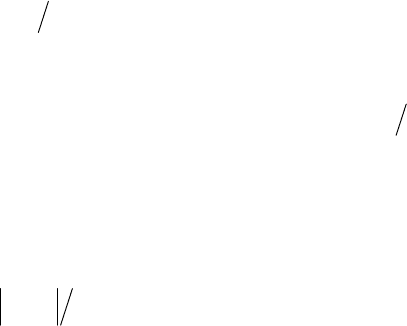
6.2.5. Округление численных оценок параметров регрессионной модели
Статистик, работающий с химиками или инженерами, может дискредитировать
себя необдуманным предложением доверительного интервала такого вида 7,32179 ± 0,05248
вместо 7,32 ± 0,05 или использованием углового коэффициента прямой с семью знаками,
когда сама прямая была подобрана по данным с тремя знаками. Г. Шеффе [1, с. 77]
Недостаток математического образования, прежде всего, сказывается в чрезмерной
точности вычислений (Хаген).
Большинство задач экспериментального исследования завершается построением
регрессионной модели (РМ) исследуемого объекта [2]. Обычно численные оценки параметров РМ
(коэффициенты b
i
→
β
i
и остаточная дисперсия S
2
→
σ
2
) записываются с чрезмерно большим
количеством (от четырех до девяти) цифр [2 с. 358], часть которых является незначащей. Это
приводит к иллюзорному представлению о большой точности оценок, повышает вероятность
совершения ошибки при переписывании чисел, увеличивает объем вычислительных работ с
незначащими (лишними) цифрами и выглядит неуместно.
Правило округления статистической оценки описано в литературе [3]. Однако
использование этого правила для округления коэффициентов РМ b
i
зачастую приводит к тому,
что нормальная остаточная ошибка Е ~ N(
ν
,
σ
2
) (с центром
ν
= 0 и дисперсией
σ
2
> 0) РМ с
неокругленными коэффициентами b
i
превращается в существенно худшую ошибку Е
0
~ N(
ν
0,
σ
0
2
)
РМ с округленными коэффициентами b
i0
: значимо возрастает остаточная дисперсия (
σ
0
2
>
σ
2
);
появляется значимая систематическая составляющая ошибки (
ν
0
≠
0).
Это объясняется тем, что упомянутое правило справедливо лишь для округления одной
единственной оценки. Отсюда следует, что в численных оценках коэффициентов РМ следует
оставлять большее количество цифр, чем это предписывается правилом [3].
Задачей настоящего исследования является определение зависимости количества
значащих цифр U, на которое надо увеличить оценки коэффициентов РМ по сравнению с числом
значащих цифр, которое предписывается правилом округления одной оценки, от статистических
характеристик РМ.
Приведем сначала обоснование правила округления одной оценки
ˆ
θ
параметра
θ
.
Допустим, что после округления оценки
ˆ
θ
параметра
θ
получится оценка
0
ˆ
θ
другого
параметра
0
θ
, не равного
θ
. Это позволяет сформулировать нулевую гипотезу H
0
о том, что
неокругленная оценка
ˆ
θθ
→
и округленная оценка
00
ˆ
θθ
→
однородны, т. е. H
0
:
0
0
θθλ
−==
против альтернативной гипотезы об их неоднородности H
1
: λ
≠
0 (здесь λ - разность параметров
θ
и
0
θ
). Проверочную статистику запишем в виде Z =
ˆ
ˆ
S
λ
λ где
ˆ
λ
- оценка разности параметров
θ
и
0
θ
,
0
ˆˆˆ
λθθ
=−
;
ˆ
S
λ
- среднеквадратичное отклонение (CO) ошибки разности.
Для построения правила округления оценки с некоторым запасом точности введем
следующие допущения. Положим, что
ˆ
S
λ
=
ˆ
S
θ
, где
ˆ
S
θ
- CО оценки
ˆ
θ
; величина Z =
ˆ
ˆ
S
θ
λ
подчинена нормальному закону распределения с центром в нуле и дисперсией, равной единице, то
есть Z ~ N(0, 1). Принимая "ответственность за вывод" - "предельно большую" [4] (см. также табл.
2 в разделе 1) и учитывая, что "предпочтительной" является гипотеза H
0
, зададим очень большое
критическое значение уровня значимости α
ко
= 0,6 (этому числу соответствует верхнее
критическое значение нормированного нормального распределения Z
0,6/2
≈
0,5 [1, 3]). Тогда
условие, при котором гипотеза H
0
не отклоняется, приобретёт вид [4]
Z
0,3
≈
0,5 >
ˆ
0
ˆˆ
ˆ
ZS
θ
θθ=−
. (1)
Легко показать, что этому условию удовлетворяет следующее правило [7, с. 251]. Для
округления абсолютного численного значения одной оценки
ˆ
θ
необходимо в числе
ˆ
θ
отбросить
цифры младшего разряда, начиная с цифры, соответствующей второй цифре наибольшего разряда
СО оценки
ˆ
S
θ
. Последнюю из оставшейся в округленной оценке
0
ˆ
θ
цифру увеличивают на
единицу, если первая из отбрасываемых цифр больше или равна 5.
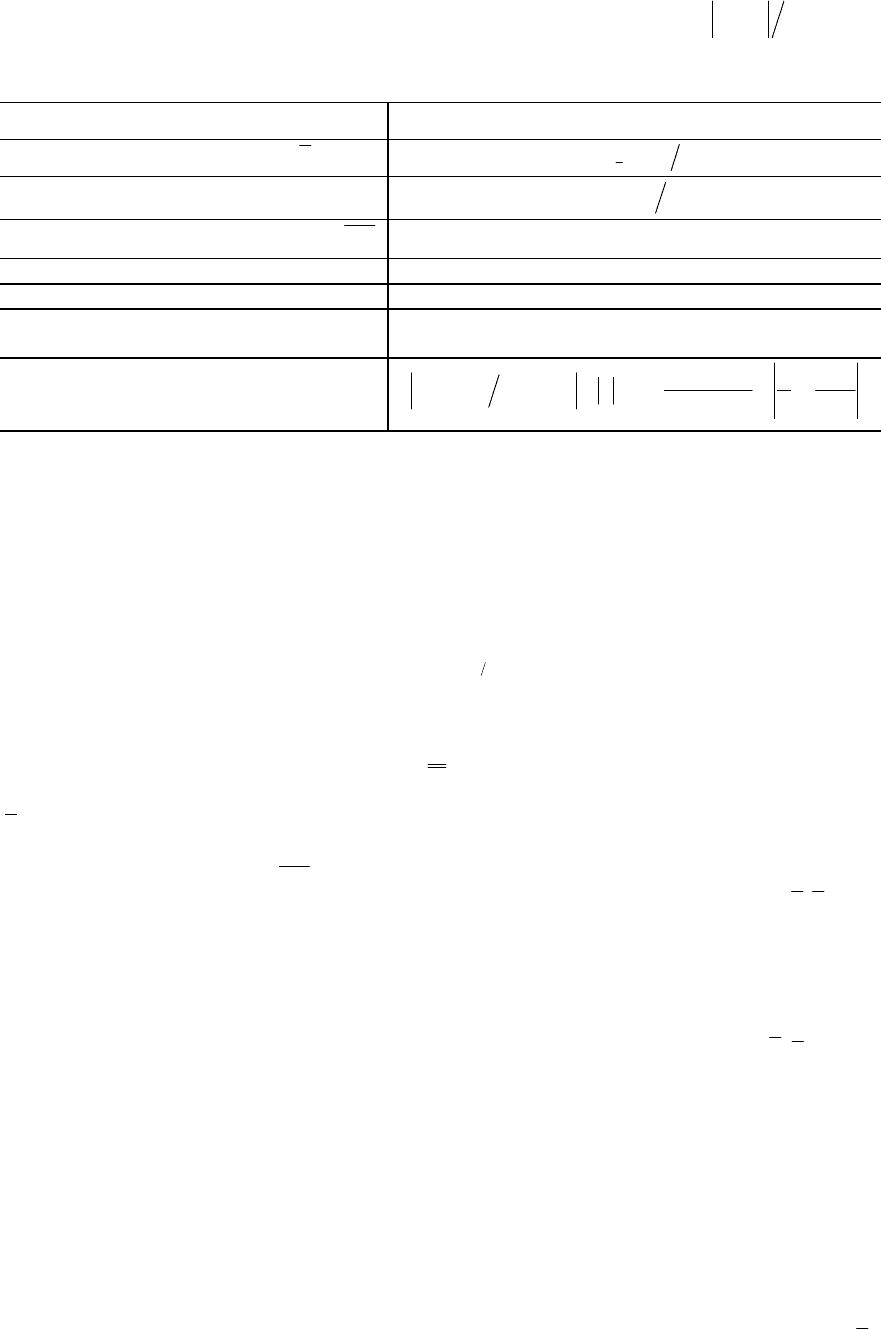
Действительно, согласно этому правилу, максимум числителя отношения
ˆ
0
ˆˆ
S
θ
θθ− равен
0,4(9)*10
к
, к
∈
N, минимум знаменателя
ˆ
S
θ
= 1, что и удовлетворяет неравенству (1).
Приведем некоторые статистические оценки, используемые в регрессионном анализе:
Точечная (однозначная) оценка
ˆ
θ
CO ошибки оценки,
ˆ
S
θ
Среднее значение,
x
0,5
xx
SSN
=
CO величины x, S
x
()
0,5
2
Sx
SSN=
Коэффициент регрессии,
,1,
i
bim
=
i
bii
SSC
=
Коэффициент асимметрии, А S
A
= (6/N)
0,5
; (N > 30)
Коэффициент эксцесса, Э S
Э
= (24/N)
0,5
; (N > 50)
Нормированное среднее абсолютное
отклонение, H
S
Н
= 0,4/N
0,5
; (N > 25)
Коэффициент корреляции r
(при N > 9)
()()
()
22
0,5
111
11;ln
21
3
VV
r
eerV
r
N
+
−+−=+
−
−
Здесь N - объем выборки; S - CO остаточной ошибки РМ; C
ii
- диагональный элемент
обратной матрицы [2, с. 118]; m - число коэффициентов. В связи асимметричной плотностью
распределения статистики r, в таблице вместо оценки S
r
приведено значение меньшего плеча 68%-
ного доверительного интервала.
Пример 1. Пусть CO
ˆ
S
θ
= 0,014. Тогда статистическую оценку
ˆ
θ
, равную 1,0648553 можно
округлить до значения
0
ˆ
θ
= 1,06, а оценку
ˆ
θ
= 1,995047 - до
0
ˆ
θ
= 2,00.
Здесь надо отметить, что в работе [3] для округления оценки
ˆ
θ
вместо числа
ˆ
S
θ
используется
число
ˆ
S
θ
/3; уменьшение критического значения
0
2
k
Z
α
в выражении (1) в три раза соответствует
чрезмерно завышенному критическому уровню значимости
0
k
α
= 0,87.
Теперь приведем обоснование правила округления оценок коэффициентов РМ.
Пусть по известным матрице плана
X
размерностью (
Nk
×
) и вектору откликов
12
,,...,
N
YYYY
=
&
методом наименьших квадратов получены неокругленные численные
оценки b
i
(в большинстве программ ЭВМ используется от шести до девяти якобы «значащих»
цифр) коэффициентов β
i
(
1,
im
=
) эмпирической функции регрессии (ЭФР)
(
)
ˆ
ˆ
,
Yfxb
= ; CO
ошибок этих коэффициентов -
i
b
S
; CO остаточной ошибки РМ S
→
σ
. Необходимо округлить
численные оценки b
i
коэффициентов РМ.
Допустим, что после округления оценок b
i
получены оценки b
i0
других параметров β
i0
,
приводящих к смещению центра распределения ошибки Е модели регрессии
(
)
,
YfxE
β
=+
на
величину ν
0
≠
0 и
дисперсии
σ
2
на величину
σ
α
2
> 0. Это позволяет сформулировать одну пару
гипотез относительно центра распределения ошибки Е
Н
10
: ν
0
= 0; Н
11
: ν
0
≠ 0. (2)
Для формулировки второй пары гипотез относительно дисперсии величины Е будем
считать, что приращение
σ
α
2
дисперсии
σ
2
пренебрежимо мало по сравнению с дисперсией
σ
2
,
если величина
σ
α
2
не превышает дисперсии
σ
S
2
CO S. Приходим к гипотезам
Н
20
:
σ
α
2
≤
σ
S
2
; Н
21
:
σ
α
2
>
σ
S
2
. (3)
Объединяя гипотезы (2) и (3), приходим к одной нулевой гипотезе H
0
, являющейся
конъюнкцией Н
10
и Н
20
, против альтернативы Н
1
, являющиеся дизъюнкцией Н
11
и Н
21
:
Н
0
: Н
10
∩
Н
20
; Н
1
: Н
11
∪
Н
21
. (4)
Как и прежде, для построения правила округления оценок с большим запасом точности,
возьмем в качестве статистической характеристики гипотезы H
10
отношение величины
0
e
-
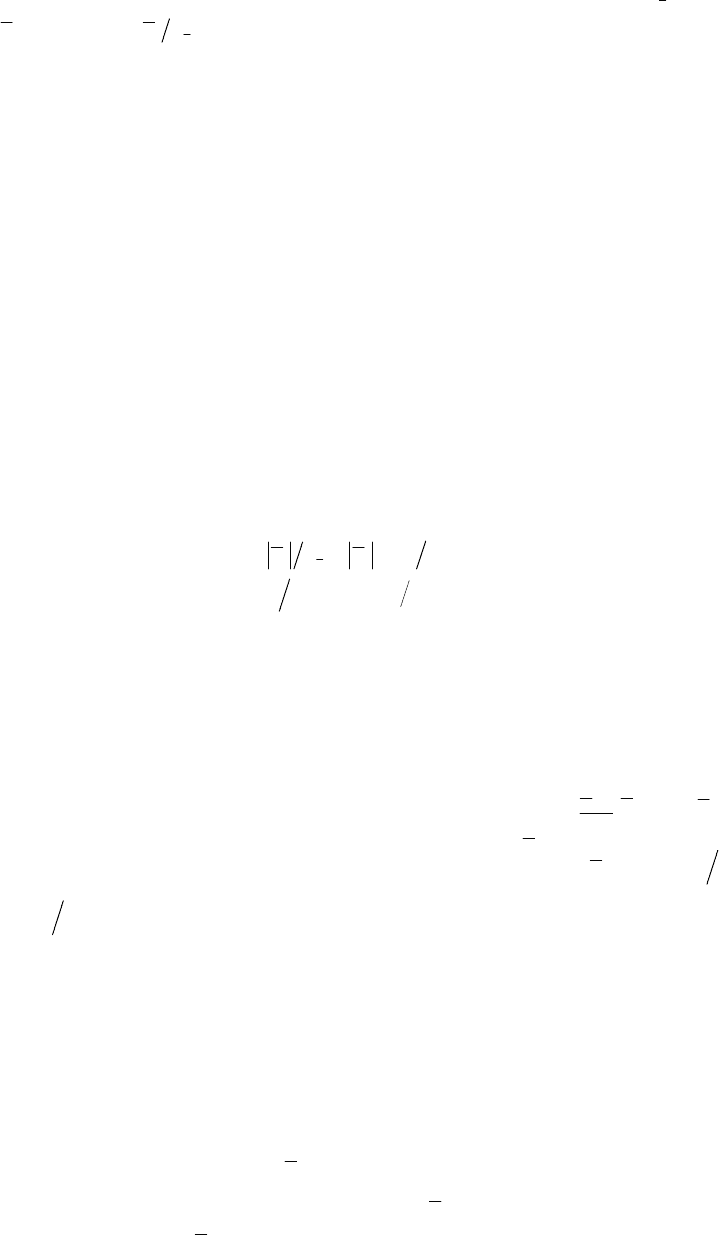
среднего значения остатков после округления коэффициентов PM к величине
e
S
- CO ошибки
среднего
e
остатков РМ:
0
e
eS
= Z, Z
∼
N(0, 1).
Статистика S
2
после округления коэффициентов примет значение S
0
2
с f
0
степенями свободы.
Оценку S
α
2
дисперсии
σ
α
2
находим по формуле S
α
2
= S
0
2
- S
2
. Оценку S
S
2
дисперсии
σ
S
2
находим по формуле [5, c. 207]: S
S
2
= S
2
/(2f) с числом степеней свободы f. Ввиду независимости
дисперсии S
S
2
и S
α
2
, в качестве статистической характеристики гипотезы H
20
можно выбрать
фишеровское отношение
ˆ
F
= S
α
2
/S
S
2
(5)
с f
α
и f степенями свободы.
Зададим очень большое значение критического уровня значимости α
ко
= 0,75. Всего имеется
две альтернативные гипотезы (4).
Можно показать [4], что условие, при котором гипотеза Н
0
не отклоняется, имеет вид
{}
(
)
2
ˆˆˆ
11min,
ZF
ααα=−− ≥ α
ко
, (6)
где
ˆˆ
,
ZF
αα
- оценки уровней значимости статистик
ˆ
Z
и
ˆ
F
.
Зададим
ˆˆ
ZF
ααα
==
%
и решим неравенство (6) относительно
α
%
. Получим
α
%
≥ 1 - (1 - α
ко
)
1/2
=
α
%
ко
. (7)
Подставив сюда α
ко
= 0,75, получим критическое значение уровня значимости для проверки
каждой из двух гипотез:
α
%
ко
= 0,5. Теперь видно, что число α
ко
= 0,75 было выбрано так, чтобы
критические значения критериев Z
к
и F
к
можно было задать достаточно малыми [3] Z
к
≈
0,7 и F
к
≈
1 для всех f и f
α
. Это позволяет записать условия, при которых гипотеза H
0
(4) не отклоняется:
0,5
00
ˆ
0,7;
ek
ZeSeNSZ==<≈ (8)
(
)
2222
0
ˆ
211
Sk
FSSfSSF
α
==−<≈
. (9)
Теперь опишем процедуру (или правило) округления коэффициентов PM.
Установить число значащих цифр в коэффициентах PM по сформулированному выше
правилу округления одной единственной оценки. (Для этого использовать значения
коэффициентов b
i
и CO их ошибок
i
b
S
).
Определить такое целое число U, на которое следует дополнительно увеличить число
значащих цифр в записи чисел всех коэффициентов РМ.
Начать с нулевого приближения (U = 0). Найти остатки
(
)
0
,
iuiui
eYfBX
=−
, где
0
u
B
- вектор
округленных значений коэффициентов РМ;
i
Y
- координата вектора
; 1,
YiN
=
.
Вычислить значения составляющих остаточной ошибки: среднее
0
1
N
uiu
i
eeN
=
=
∑
и СО
()
0,5
2
0
1
N
uiu
i
SeNm
=
=−
∑
.
Проверить справедливость условий (8) и (9). Если хотя бы одно из этих условий не
удовлетворено, увеличить число значащих цифр в округляемых коэффициентах РМ еще на одно
(заменить U на U + 1) и возвратиться к проверке условий (8) и (9). Если оба условия (8) и (9)
удовлетворены, то выбор числа U завершен.
Указанный алгоритм был опробован в программе регрессионного анализа REGAN (ЭВМ
ЕС-1045; язык PL/1; программа была написана супругами Рудаём А. Н. и Рудай В. И. [8].
Пример 2.
По результатам наблюдений (X
1i
X
2i
Y
i
) = (31 40 21), (76 73 70), (64 63 59), (70 52
73), (28 20 30) получены численные оценки параметров РМ Y = 1,51714X
1
- 0,606018X
2
- 0,963837 с
вектором CO ошибок коэффициентов
b
S
= (0,0585829; 0,0642270; 1,51260)
Т
и CO остаточной
ошибки S = 1,15762. Необходимо округлить полученные статистические оценки параметров.
Решение. Выразим условия (8) и (9) относительно
0
e
и S
0
(при N = 5 и f = N – m = 2):
|
0
e
| < 0,7S/N
0,5
= 0,362; S
0
< S (1 + 1/(2f))
0,5
= 1,29. (10)
Установим в нулевом приближении (U = 0) число значащих цифр в коэффициентах РМ по
правилу округления одной оценки. С помощью полученной РМ Y = 1,52
⋅
X
1
- 0,61
⋅
Х
2
- 1 найдем
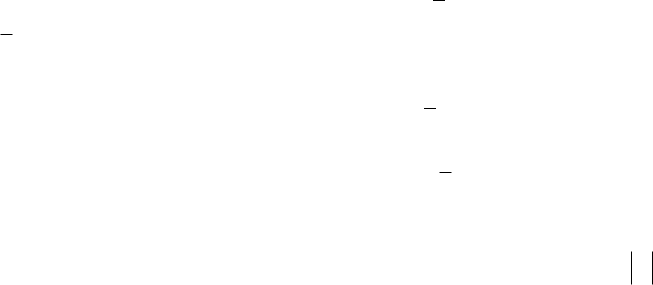
остатки e
i0
= (- 0,72; 0,01; 1,15; - 0,68; 0,64)
т
, а по ним - среднее
00
e
= 0,08 и CO S
00
= 1,16.
Полученные значения
00
e
и S
00
удовлетворяют условиям (10).
Ответ. Вектор округленных значений коэффициентов ЭФР
0
B
= (1,52 - 0,6I - 1 )
Т
; CO
остаточной ошибки S
0
= 1,2.
Для реализации описанного алгоритма на ЭВМ необходимо затратить определенные усилия,
а общее время расчета увеличивается за счет вычисления величин
0
u
e
и S
0u
. Можно достичь
экономии усилий и времени расчета, если воспользоваться эмпирической зависимостью величины
U от следующих характеристик РМ: K - числа базисных функций; f - числа степеней свободы;
F
и
= S
2
об
/ S
2
- информационного отношения, где S
2
об
- общая дисперсия отклика;
{
}
1
max
ij
ijK
rr
≤≤≤
=
-
максимального из абсолютных значений недиагональных элементов r
ij
корреляционной матрицы
базисных функций; ϕ = K
r
/M - отношения числа K
r
значимо отличающихся от нуля
коэффициентов корреляции из этой матрицы к общему числу M коэффициентов корреляции
(М = К(К - 1)/2); F
M
- критерия мультиколлинеарности базисных функций по Фишеру [6, с. 326].
Статистический материал, необходимый для получения этой зависимости, заимствован из
25-ти наших работ, список которых приведен в статьях [4] и [8].
При округлении коэффициентов в 92-х РМ нашли, что U = 0 в 60% случаев; U = 1 в 29%;
U = 2 в 12% случаев. Так что если принять U = 2, то это будет верно в 12% случаев, приведет к
завышению (к запасу) на один знак в 29%, на 2 - в 60% случаев. Точнее определить U можно с
помощью эмпирической формулы
ˆ
U
= E{1,6 - 0,24lgF
и
- 0,107(K - 1)lg(1 - r
m
)}, (11)
где E{⋅} - операция округления до целого числа.
Область определения формулы (11): 1
≤
K
≤
7; 1
≤
f
≤
1140; 1
≤
F
и
≤
4800; 0
≤
r
m
≤
0,999;
0
≤
ψ
≤
1; 1
≤
F
M
≤
1300.
Формула (11) получена методом регрессионного анализа [использовались базисные функции
lgf, lg F
и
, K - 1, (K - 1) lg F
и
, (K - 1) lg f, (K - 1) lg (1 - r
m
), (K - 1)ψ и (К - 1)lg(F
M
+ 1)].
Для того чтобы погрешность формулы (11) не превышала нуля, ее свободный член увеличен
на 0,94. Поэтому использование формулы (11) приводит к верному значению U в 33% случаев, к
завышенному (то есть с запасом) на один знак - в 55%, на 2 - в 12% случаев.
Литература
1. Шеффе Г. Дисперсионный анализ. - M.: Наука, 1980. - 517 с.
2. Дрейпер H.
,
Смит Г. Прикладной регрессионный анализ. Кн. 1, - M.: Финансы и
статистика
,
1986. - 366 с.
3. Урбах В. Ю. Биометрические методы. - M.: Наука, 1964. - 380 с.
4. Цейтлин Н. А. Применение методов математической теории эксперимента в содовой
промышленности. Обзорная информация. Серия "Содовая промышленность". - M.:
НИИТЭХИМ, 1984. - 48 с.
5. Смирнов H. B.
,
Дунин-Барковский И. В. Курс теории вероятностей и математической
статистики для технических приложений. -M.: Наука
,
1965, - 512 с.
6. Андерсон T. Введение в многомерный статистический анализ. - M.: Физмaтгиз
,
1963. -
500 с.
7. Демидович Б. П., Марон И. А. Основы вычислительной математики. - M.: Наука. 1970.
- 664 с.
8. Рудай А. Н., Цейтлин Н. А., Рудай В. И., Ицков Ф. Э. Разработка рациональных
процедур для программы линейного регрессионного анализа. Статистические методы в
основной химии: Труды. Т.63/НИОХИМ. - Харьков, 1986. - с.72-84.

6.2.6. Разработка рациональных процедур программы
линейного регрессионного анализа.
Иррациональность Бога в том, что он не три-един, как все думают, а пи-един! (Из интернета)
В давние времена, когда президент Рейган был еще простым «народным артистом» США,
нами (в соавторстве) был произведен на свет программный продукт под названием РЕГАН
(РЕГрессионный АНализ) [16.41, 16.52]. По нашему мнению, это была самая лучшая (для нас) из
известных (нам) программ! Почему? Мы воспользовались лучшей (в то время) программой
регрессионного анализа (а нынче это могут быть, например, - ППП STATISTICA [10.15, 10.16,
http://www.statsoft.ru], SPSS [10.19, http://www.SPSS-buch.de], SAS [www.sas.com] и др.) и дополнили
её сервисными процедурами пользователя, которые разработали сами. Программа РЕГАН (и ей
подобные) совершенствуется АСом самостоятельно. В нашей версии [16.52] в программе РЕГАН
комплексно и всего за один подход к ЭВМ «интегративно» [1.27.] решались многие часто
встречаемые задачи регрессионного анализа.
В настоящее время пользователю статистических программ не составит большого труда
дополнить стандартные процедуры пакета программ по регрессионному анализу
дополнительными рациональными процедурами, некоторые из которых описаны, например, в
одноименной статье (Рудай А. Н., Цейтлин Н. А., Рудай В. И., Ицков Ф. Э. - В кн.: Технология и
автоматизация содового и смежных производств: Труды, т. 61/НИОХИМ. Харьков, 1985, с.72 -
84).
Практика построения математических моделей химико-технологических систем вообще и в
содовой промышленности [1-9], в частности, свидетельствует о том, что наиболее мощным
методом статистической обработки данных является
регрессионный анализ (РА)
. Программы РА
непрерывно рационализируются [10-17] в зависимости от особенностей решаемых задач в
предметной области, достижений статистической теории и интересов авторов программ.
Для обработки данных методом РА авторы использовали вначале стандартные процедуры
МО ЭВМ по статистике [12]. Однако, при решении каждой задачи возникали трудности, для
преодоления которых приходилось разрабатывать новые рациональные процедуры. Собранные
воедино (с помощью головной программы), эти процедуры составили пакет программ РА
(названный «РЕГАН»).
В настоящей работе изложены основные идеи и приемы, использованные при составлении
упомянутых процедур.
Функциональное преобразование признаков (ФПП)
Методы структурной идентификации регрессионной модели - сложная наука, а иногда
даже – искусство! Сначала следует подобрать и обосновать исходную структуру регрессии,
включающую все подозреваемые факторы, создать соответствующие базисные функции, или
ФПП, а только потом программа выбирает наилучшее в каком-то смысле подмножество базисных
функций. Например, теория подобия даёт структуру мультипликативных функций регрессии при
описании процессов в движущейся среде, в частности, - гидродинамики процессов массопереноса
(см. [Р6.3.1.2]). Можно подобрать дифференциальные уравнения этих процессов, интегралы
которых и дают обоснованную теорией структуру регрессионной функции, известную лишь с
точностью до параметров, которые, в свою очередь, и определяются по экспериментальным
данным. В ряде случаев удобно использовать ортогональные полиномы Чебышева, сплайн -
функции, функции Фурье и многие другие [17].
Обычно ФПП в программах РА осуществляется с помощью небольшого количества
встроенных функций [11]; для более сложных ФПП пользователю рекомендуется писать
собственную процедуру на алгоритмическом языке.
Процедура ФПП успешно используется для построения регрессионных моделей в основной
химической технологии (табл. 1).
Таблица 1
Некоторые функциональные преобразования признака, использованные для построения
регрессионных моделей в основной химической технологии (примеры)
Источник Функциональное преобразование признака
[2] X
1
/X
2
; lgX
2
; (X
1
/X
2
)
2
lgX
2

[3]
|X
1
– 50|; 0 при Х
∈
(0,825; 1]; 1 при Х
∈
(0,825; 1]
[4, 5]
1
0 npu 0,4;
Х
≤
()
3
1
0,4 npu 0,4
ХХ−>
[5] sin(16,03X
1
); cos(16,03X
1
)
[6]
1,5423
1
0,59849/(43,252);
Xη =+
(lg(X
2
/η))/X
3
[7, 8]
1
2arcsin
X
; X
1
+ (24(30,14(X
2
– 1) + (X
3
– 1)) + X
4
)/8760
[9]
1 при Х
1
= 3; 0 при Х
1
≠ 3.
Для обобщения данных по газопарожидкостному равновесию используются рациональные
функции, логарифмы и т. п. [2]; для аппроксимации сложных физикохимических функций (кривых
ликвидуса и солидуса, удельной теплоты кристаллизации и т. п.) используются абсолютные
величины, ступенчатые [3], усеченные функции [4,5] (в составе сплайн-функции) и члены ряда
Фурье [5]; для расчета параметров физических свойств растворов электролитов используются
полуэмпирические функции, имеющие определенный физический смысл (например, зависимость
вязкости η воды от температуры Х
2
в табл. 1) [6]; при расчете к. п. д. процесса каталитического
окисления оксида углерода пришлось использовать нормализующее преобразование отклика [7];
поиск зависимости событий от времени года приводит к преобразованию переменных,
кодирующих год (Х
1
), месяц (Х
2
), день (Х
3
), час (Х
4
) к одной переменной, определяющей момент
времени с точностью до часа [8]; для перекодирования качественных переменных, измеряемых с
помощью шкалы наименований, из чисел натурального ряда в вектор – код, используются
единичные импульсные функции [9].
Процедура ФПП использована также в программах табулирования функций,
дискриминантного анализа и др.
Редукция корреляционной матрицы (РКМ)
Процедура РКМ позволяет компактно представить большую КМ так, чтобы значения
каждого коэффициента корреляции были представлены одним символом R
∈
{0, 1, 2 …, A, B, …}
в верхней треугольной матрице, а знаки – в нижней. Каждый символ R соответствует центру
своего интервала статистической не значимости.
Отбор существенных факторов (ОСФ)
Высокую оценку специалистов [13] получил метод ОСФ Эфроимсона [14]. В этом методе
используется пошаговая процедура включения факторов. Составляется множество
«подозреваемых» (в том, что они могут быть значимыми) факторов (точнее – базисных функций).
На каждом шаге в регрессию включается фактор, который имеет максимальный частный
коэффициент корреляции с откликом и проверяется значимость всех коэффициентов регрессии.
Если на некотором шаге какой-либо коэффициент оказался незначимым, соответствующий ему
фактор на следующем шаге исключается из регрессии; если же фактор при незначимом
коэффициенте был включен на данном шаге, процедура выходит на конец расчета.
В предлагаемой процедуре ОСФ используется
метод серий
, несколько отличающийся от
метода Эфроимсона. В методе серий используется возврат поиска не на 1, а на п > 1 шагов назад в
сочетании с варьированием уровня значимости.
ОСФ начинается также пошаговым включением факторов. Если на некотором шаге какой-
либо коэффициент, например, b
j
оказался незначимым, то возврат процедуры поиска
осуществляется на п шагов назад (п > 1) к тому шагу, на котором соответствующий коэффициенту
b
j
фактор Х
j
впервые попал в регрессию. Начинается новая серия включений факторов. В этой
серии фактор Х
j
исключается из поиска п раз; на шаге п + 1 фактор Х
j
включается в число
«подозреваемых» вновь. Если окажется, что п = 1 (то есть незначимым оказался последний из
включенных в регрессию факторов), процедура выходит на конец расчета. Метод серий позволяет
получить несколько большее, чем в методе Эфроимсона, число полезных [17, с. 361] (со всеми
значимыми коэффициентами и приблизительно равными минимальными остаточными
дисперсиями) функций регрессии, предъявляемых исследователю как множество решений задачи.
Варьирование уровня значимости
Согласно α-методу проверки гипотез [1] значимость коэффициента регрессии b
j
характеризуется уровнем значимости
ˆ
j
α
; чем меньше
ˆ
j
α
, тем значимее отличие абсолютной
величины коэффициента регрессии от нуля. Если
ˆ
j
α
меньше некоторого критического уровня
α
к1
(например,
α
к1
= 0,01), то соответствующий коэффициент b
j
считается значимым.
При ОСФ рекомендуется [13, с. 182] «временно» использовать высокое значение α
кв
критического уровня значимости α
к
(например, α
кв
= 0,9 [1]). Наш опыт показал, что в этом случае
программа на двух-трех шагах включения может включить не очень значимые коэффициенты b
j
(с
уровнем значимости
1
ˆ
0,9
ki
αα
<<
), зато на следующих шагах значимость всех коэффициентов
может резко возрасти (
1
ˆ
ik
αα
<
).
Таким образом, дополнительное число полезных эмпирических функций регрессии (ЭФР)
можно получить «краткосрочным» установлением повышенного уровня значимости
α
кв
. После
завершения расчетов программа выводит на печать полезные ЭФР с коэффициентами, значимыми
на «обычном» уровне значимости (
ˆ
i
α
<
α
к1
).
Экономия памяти ЭВМ
Для реализации метода Эфроимсона обычно используется расширенная матрица дисперсий-
ковариаций А [13, с. 18] размерностью (2к + 1)⋅(2к + 1), где к – общее число факторов.
Экономии памяти ЭВМ удается достичь путем использования всего двух матриц дисперсий-
ковариаций – основной, Д, размерностью (к + 1)⋅(к + 1) и вспомогательной альтернативной
матрицы Е, изменяющей свою размерность от шага к шагу при ОСФ от 2⋅2 до (к + 1)⋅(к + 1). Над
матрицей Е производятся преобразования по методу сокращения Дулиттла [12, с. 244].
Обработка массивов с пропущенными данными (ПД)
В процедуре ПД используется метод попарного вычеркивания [15, с. 192; 11, с. 37],
основанный на расчете ковариационной матрицы переменных (Д) и вектора средних значений.
Если пропущенные данные имеются среди значений отклика, то из массива данных исключаются
все строки, соответствующие пропускам в отклике. Можно показать, что в противном случае
оценка вектора коэффициентов окажется смещенной.
Элемент массива считается пропущенным данным, если он не является числом. В процессе
вычислений формируется (и распечатывается) матрица К, элементами которой являются
количества полностью заполненных строк для каждой пары столбцов (исходных и
преобразованных данных).
Для вычисления числа степеней свободы статистических характеристик функции регрессии,
полученных с помощью матрицы Е, используется среднее гармоническое подмножество
элементов матрицы К, соответствующих вошедшим в ЭФР переменным.
Когда проводится анализ остатков лучшей ЭФР, остатки и другие статистические
характеристики вычисляются по тем строкам, которые полностью заполнены для вошедших в
ЭФР переменных.
Лучшая функция регрессии (ЛФР)
Процедура ЛФР выбирает из множества полезных ЭФР одну с минимальной остаточной
дисперсией. Для ЛФР на АЦПУ распечатывается корреляционная матрица коэффициентов
регрессии [9], приводятся остатки и диаграмма их рассеивания [17], критерии согласия
распределения остатков с нормальным распределением [1], интервальные оценки функции
регрессии [13], критерий мультиколлиниарности факторов, включенных в регрессию [18, с. 326].
Исправление ошибочных значений отклика (ОЗО)
Большинство экспериментальных точек (от 90 до 99%) лежат в пределах области
допустимых значений отклика (с заданной вероятностью, например, 95%). Однако некоторые
точки «имеют право» выпрыгивать за границы этой области. И только 1 – 2 слишком далёких
«выброса» могут вызвать у нас подозрение в том, что они не принадлежат к изучаемой
совокупности. Их наличие проверяют по критериям «выброса». Принято считать (хотя это и не
обязательно), что выбросы являются ОЗО.
Обычно ОЗО обнаруживают с помощью критерия Смирнова-Груббса [19, с. 101] и
исключают из расчетов всю строку данных (опыт). Потеря целой строки невыгодна для анализа.
Поэтому рекомендуется использовать процедуру «исправления» ОЗО (аналогично винсоризации
средних значений [20, с. 177]). Для этого в первом цикле расчетов с помощью процедуры ОСФ
получают ЛФР. задают критический уровень значимости α
к0
[1] в предположении о наличии
одного (q = 1) ОЗО. Выявляют ОЗО по N остаткам ЛФР с помощью критерия Смирнова-Груббса.
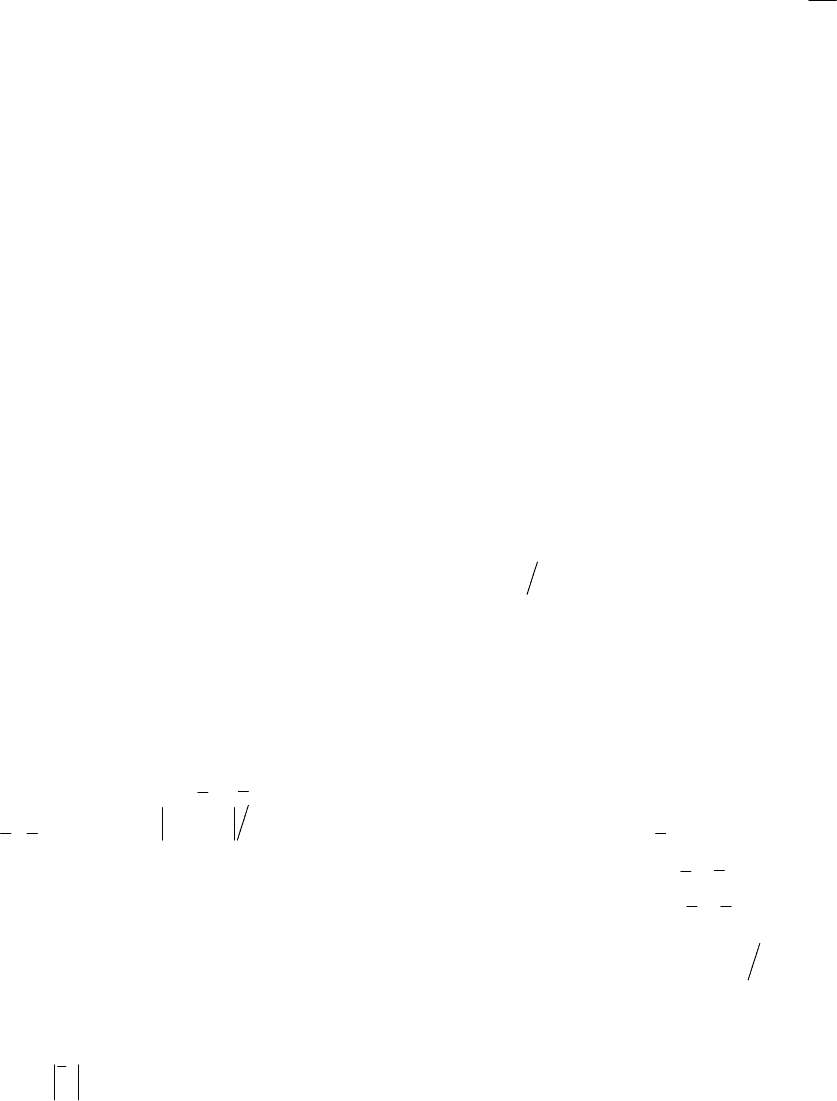
Если одно ОЗО выявлено, принимают q = 2 и корректируют критический уровень значимости
()1/
00
1(1),1
qq
kk
qαα
=−−≥
. (1)
После обнаружения вторичного ОЗО принимают q = 3 и т. д., пока не будут найдены все Т
ОЗО (0
≤
Т < N – f, где f – число параметров РМ.). Затем все Т выявленных ОЗО
i
Y
(i =
1,
T
)
заменяют значениями отклика
ˆ
i
Y
, вычисленными по ЛФР, и переходят к следующему циклу
расчетов. В следующем цикле с помощью процедуры ОСФ вновь получают ЛФР, выявляют ОЗО и
т. д. Расчеты продолжаются до тех пор, пока ОЗО не перестанут появляться. Полученные во всех
циклах расчетов «полезные» ЭФР выводятся на печать. Опыт показывает, что один-два ОЗО
появляются, в среднем, в каждом третьем расчете.
Замечание. Некоторые исследователи ошибочно полагают, что экспериментальные точки
«не имеют права» выходить за пределы доверительного интервала, построенного вокруг линии
регрессии. В связи с этим отметим, что доверительный интервал строится не для
экспериментальных точек, а для условного математического ожидания отклика. При
необходимости, и для заданной доли экспериментальных точек с заданной вероятностью может
быть построена область допустимых значений отклика [4.2.].
Проверка адекватности эмпирической функции регрессии
Адекватность ЭФР обычно проверяют путем сравнения остаточной дисперсии
2
0
Y
S
с
дисперсией воспроизводимости отклика
2
boc
S
[21, с. 151]. Если выборка объемом N элементов
включает М параллельных опытов, когда L < M < N, где L – число коэффициентов ЭФР,
остаточная дисперсия
2
0
YM
S
с N – L степенями свободы вычисляются по программе РА со
смещением. Пользуясь разложением накопленной суммы квадратов остатков [21, с. 181],
получили несмещенную оценку остаточной дисперсии с М – L степенями свободы:
(
)
(
)
(
)
222
00YYMboc
SSNLSNMML
=−−−−
. (2)
Когда в исходной выборке отсутствуют параллельные опыты (в случае пассивного
эксперимента), используют итерационную процедуру построения ЛФР и вычисления смещенной
оценки дисперсии воспроизводимости отклика по почти параллельным опытам [1, 22, 23].
Дисперсия воспроизводимости отклика (ДВО)
Процедура ДВО позволяет с помощью полученной ЛФР на множестве точек плана найти
почти параллельные опыты и по ним оценить ДВО. Почти параллельные опыты являются
опыты Y
i
, Y
j
в точках
i
x
,
j
x
факторного пространства, для которых справедливо условие
(
)
1
,1
k
ij
ijrirjr
r
xxDxxL
=
Φ=−<
∑
, где x
ir
– r-тая координата вектора
i
x
; D
ijr
- максимум
частной производной ЛФР по x
r
, взятый на отрезке прямой с концами в точках
i
x
,
j
x
; величина L
выбирается из условия принятия гипотезы о равенстве значений ЛФР в точках
i
x
,
j
x
: L = 2,8SN
-
0,5
, где S – среднеквадратическое отклонение (СО) остатков; N – объем выборки. Смещенная
оценка ДВО определяется по l парам почти параллельных опытов:
(
)
()
()
2
2
,
2
cij
ij
SYYl
=−
∑
.
Округления коэффициентов регрессии (ОКР)
Процедура ОКР [26] позволяет распечатывать значения округленных коэффициентов
регрессии в соответствии со следующими ограничениями погрешностей: систематическая ошибка
остатков
0,5
0
0,7eSN
−
< ; СО остаточной ошибки S
0
< S[1 + 0,5(N – q)
-1
]
0,5
, где q – число КР.
Область определения регрессионной модели (ООМ)
Пространство факторов при неоптимальном планировании экспериментов, как правило, не
образует прямоугольную фигуру (гиперпараллелепипед). Например, при корреляции двух
факторов ООМ может быть эллипсом, сильно вытянутым вдоль случайно ориентированной
главной оси. Задавая в таком случае ООМ в виде прямоугольника, мы ошибемся, включив
части области, на самом деле не принадлежащие ООМ. Если же рассматривать вектор
факторов как псевдослучайный нормально распределенный вектор, то ООМ как область
