Цейтлин Н.А. Из опыта аналитического статистика

Подождите немного. Документ загружается.

6.3.1.2. Процессы и аппараты химических производств. Исследование гидравлического

сопротивления сухих опорных решеток со взвешенной насадкой разного типа

В одноимённой работе (Тарат Э. Я., Моисеев В. Ф., Смоляк В. Д. Цейтлин Н. А. Журн.

прикл. химии №12, т. 58, 1980, с. 2710-2714.) описана первая (в подобном исследовании) попытка

подхода к решению задачи получения аппроксимирующих и корректно интерпретируемых

регрессионных моделей. Использовать в опытах ортогональный план не было возможности, ибо

априори у авторов не имелось представления о структуре регрессионной модели. Однако

полученная апостериори модель уже может быть использована для разработки статистически

оптимального плана будущих опытов, которые позволят получить корректно

интерпретируемую модель.

В результате настоящего исследования была установлена эмпирическая зависимость

коэффициента гидравлического сопротивления сухой опорной решетки со взвешенной

насадкой от основных конструктивных параметров контактного устройства и

конфигурации насадки; кроме того, предложена методика нелинейного оценивания параметров

кусочно-непрерывной аппроксимации функции отклика, сочетающая методы нелинейного

программирования и линейный регрессионный анализ.

Для увеличения производительности аппаратов со взвешенной насадкой, повышения

эффективности межфазного контактирования и расширения диапазона их устойчивой работы

применяют тяжелые насадочные тела различной конфигурации [1-3].

В некоторых исследованиях [4-9], посвященных изучению гидродинамики и кинетики

процессов, протекающих в аппаратах со взвешенной насадкой, рассматриваются насадки

небольшой плотности; в других работах [10-13] описаны результаты исследований насадки из

стеклянных шаров плотностью 2600 кг/м

и пластмассовых колец.

В дополнение к предыдущим работам нами исследована гидродинамика сухих опорных

решеток со взвешенной насадкой, изготовленной из резины плотностью 1200 кг/м

полипропилена плотностью 370 кг/м

; форма насадочных тел: шар, минообразная и цилиндр

рифленый. Коэффициент формы составлял: для шаров - 1.0, минообразной насадки - 0,592, для

цилиндров рифленых - 0.517. Эксперименты были проведены на лабораторной установке

(стенде), описанной ранее [1].

Гидравлическое сопротивление сухих опорных решеток со взвешенной насадкой обычно

рассматривается как сумма сопротивлений опорной решетки и слоя насадки [4, 8, 14]. Однако

методики для определения коэффициента сопротивления (

) сухих опорных решеток со

взвешенной насадкой (тем более, различной конфигурации) в литературе нет. Известные

формулы [15, 16] оказались непригодными для описания результатов, полученных нами в ходе

предварительных экспериментов. Поэтому наши данные аппроксимировали эмпирической

функцией регрессии (ЭФР)

()

(

)

312

0()0

Re//

HфHB статстат

SK НН

ββ

ζβρρ

∗

, (1)

где

- коэффициенты регрессии; S

- свободное сечение опорной решетки (м

/м

); K

коэффициент формы насадки;

- соответственно плотности насадки и воды (кг/м

); Н

стат

статическая высота слоя насадки (

);

∗

стат

- стандартное значение статической высоты слоя

насадки, принятое равным 0.04 м; Re

(H)

- число Рейнольдса в слое

насадки.

Графический анализ изображения экспериментальных точек в координатах lg

- lgRe

(H)

показал, что линейная зависимость lgζ от lgRe

(H)

может иметь изломы (разрывы непрерывности

производной). Причём координаты точек излома в основном зависят от значения величины

lg(

). Зависимости с разрывом непрерывности производной часто встречаются в

гидродинамике. Их аппроксимация кусочно-непрерывными функциями является сложной задачей

регрессионного анализа [17]. Обычно опыты на прямолинейных участках группируют в отдельные

выборки и аппроксимируют их отдельными уравнениями, объединяя затем эти уравнения

условиями стыковки. Для более простого решения задачи кусочно-непрерывной аппроксимации

может быть использована

функция

, включающая в качестве базисных функций абсолютные

величины разностей [18]. Так, для аппроксимации однофакторной кусочно-линейной зависимости

отклика Y от фактора X с п изломами применялась

функция

YxXX

ββγ

=++−

∑

(2)

где β

, γ

- коэффициенты регрессии;

x - абсциссы точек излома; параметры β

, β

, γ

оцениваются методом нелинейного регрессионного анализа [19].

Результаты графической обработки наших данных позволили предположить наличие двух

изломов линейной зависимости lg

от lgRe

(H)

, где абсциссы излома

H )(

Relg являются линейной

функцией lg (

).Предположили также, что зависимость lg

от

(

)

lg/

статстат

НН

∗

имеет вид

параболы второго порядка. Если выполнить замену переменных, то

функция регрессии

, которая

по предположению будет аппроксимировать наши данные, примет вид

01122334455657181

124344

;

YXXXXXXXXXX

XCCXXCCX

βββββββββ=+++++++−+−

=+=+

(3)

где Y = lgζ; X

= lgRe

(H)

; X

= lgS

= lgK

; Х

= lg(

); Х

(

)

lg/

статстат

НН

∗

;

XX = ;

1 u

XX − ; X

1 u

XX − ;

X ,

X - абсциссы точек излома.

Нелинейный регрессионный анализ модели (3) выполнен комбинированием методов

нелинейного программирования с использованием стандартной программы линейного

регрессионного анализа [18].

Если коэффициентам C

задать некоторые значения, то отклик Y в уравнении (3) станет

линейным по остальным параметрам и оценки этих параметров MOЖHO получить по стандартной

программе. Значения C

- C

можно изменять по определенному плану так, чтобы некоторая

комбинация этих коэффициентов обеспечила минимум остаточной дисперсии отклика Y

(ограничения:

). Эта типичная задача нелинейного программирования по параметрам C

- C

с ограничениями типа неравенств решалась симплексным методом [19]. Вычислялись также t-

критерии значимости всех коэффициентов; незначимые коэффициенты исключали по одному, а

оставшиеся коэффициенты оценивали после каждого исключения. В итоге получена ЭФР

1234551

5.560.8270.210.240.7310.280.830.557,

YXXXXXXXX=−−+++−−−

(4)

где

4.6

, а t-критерии значимости коэффициентов (по порядку, начиная с

коэффициента перед X

) равны t = {24, 2.3, 3.3, 15, 2.2, 3.6, 14, 7, 2.5}. Значения t-

критериев позволяют ранжировать соответствующие факторы по силе их влияния на

отклик. Естественно, что наиболее влияющим оказался фактор X

= lg Re

(Н)

. СО остаточной

ошибки ЭФР (4) S

= 0.17 получено с 440 степенями свободы по данным 450 опытов. Поскольку

оценка отношения Фишера

/1.1

oYBY

SS=, где

- дисперсия воспроизводимости отклика,

меньше критического значения, равного 1.2 [19] со степенями свободы 440 и 450 и уровнем

значимости

= 0.05, то гипотеза об адекватности ЭФР (4) не отклонена.

Для насадки, находящейся в стационарном состоянии, число Рейнольдса определяется по

формуле

()()

(

)

/4Re aw

GGHH

, (5)

где а

- удельная поверхность статического слоя сухой насадки (м

/м

- порозность

неподвижного слоя насадки (м

/м

), ρ

- плотность газа (кг/м

), µ

- вязкость газа (Па⋅с), w

(H)

скорость газа в стационарном слое насадки (м/с); число Рейнольдса для взвешенной насадки

()()

(

)

Re4/

DGGD

Hвзв H взв

ερµ= . (6)

Скорость газа в стационарном слое сухой насадки вычисляется по формуле

()

ГH

, (7)

где w

- скорость газа в полном сечении аппарата (м/с), во взвешенной сухой насадке - по

формуле

()

DГвзвH

ww ε/=

; (8)

порозность слоя сухой насадки

= 1 – (1 - ε

) H

стат

дин

, (9)

её удельная поверхность

= а

стат

/Н

дин

. (10)

Динамическая высота слоя сухой насадки определяется ЭФР, полученной путем

аппроксимации наших данных:

(

)

(

)

()

434.0

16.0

30.0

21.023.02

Re//101.3/

HстатстатBНфOстатдин

ННKSНН

−

∗

−

⋅= ρρ (11)

t = {2.97, 3.01, 9.04, 5.30, 19.51} со СО остаточной ошибки 0.208.

Для проверки предпосылки регрессионного анализа о нормальном распределении откликов

вычисляли критерий Мизеса [20] для остатков. Поскольку для остатков ЭФР (4) расчетное

значение критерия Мизеса 0.80 меньше критического (при уровне значимости

= 0.3), равного

1.12, проверяемая гипотеза о нормальности не отклоняется [найденные дополнительно

коэффициент асимметрии остатков 0.12 и аналог эксцесса (среднее относительное отклонение)

0.772 также не отклоняет гипотезу о нормальности с α > 0.01]. Аналогичные результаты

получены для ЭФР (11). Известно [19], что корректно интерпретировать влияние каждого

отдельного фактора на отклик можно только тогда, когда он не коррелирует с другими факторами

(точнее, когда соответствующие коэффициенты парной корреляции незначимы). Нa основании

корреляционной матрицы факторов установлено, что свободным от корреляционной связи

является только фактор X

= lgS

. Это дает основание для корректной интерпретации ЭФР (4)

только по фактору X

. Характерно, что графическая обработка показывает ощутимый излом в

точке

Relg

= 3.5, в то время как статистически этот излом оказался незначимым. Это можно

объяснить, например, тесной корреляцией фактора X

с факторами X

и X

. По остальным

факторам интерпретировать уравнение (4) можно лишь приближенно. Полученная ЭФР (3) может

быть использована для разработки статистически оптимального плана [19] будущих опытов,

которые позволят построить интерпретируемую модель.

ЛИTEPАTУPА

1. Э. Я. Тарат, В. Ф. Моисеев, Г. А. Ткач. Деп. ОНИИТЭХИМ (г.Черкассы) № 1756/78 (1978).

2. В. Ф. Моисеев, Г. А. Ткач, В. Д. Смоляк и др. Авт. свид. № 614806 (1978). 3. В. Ф. Моисеев. Автореф.

канд. дис. ЛТИ им. Ленсовета (1978). 4. И. Г. Бляхер, Л. Я. Живайкин, H. A. Юровская. Хим. и нефтян.

машиностр., 2,18 (1967). 5. О. С. Балабеков, Э. Я. Tарат, П. Г. Pоманков, M. Ф. Михалев, ЖПХ, XLII, 2266

(1969). 6. Л. С. Аксельрод, M. M. Яковенко, TOXT, 3, 148 (1969). 7. В. И. Маяк, В. И. Mатрозов, TOXT, 3, 79

(1969). 8. О. С. Балабеков, Э. Я. Tарат, П. Г. Pоманков, M. Ф. Mихалев, ЖПХ, XLIV, 1061 (1971). 9. H. И.

Гельперин, Б. С. Круглов. Хим. пром., 11, 866 (1977). 10. О. С. Балабеков, П. Г. Pоманков, Э. Я. Tарат,

M. Ф. Михалев, ЖПХ, XLII, 7, 1540 (1969). 11. А. Ю. Вальдберг, H. И. Гельперин, M. M. 3aйцев и др. Хим. и

нефт. машиностр., 4, 14 (1973). 12. И. П. Левш, M. И. Ниязов, А. Убайдуллаев. Tp. Ташкентск. политехн.

инст., 64, 102 (1970). 13. Н. И. Кушнер, E. П. Левш, M. T. Hиязов. Tp. Ташкентск. политехн. инст., 91, 140

(1973). 14. А. Ю. Вальдберг, H. И. Гельперин, В. M. Тарасов. Хим. и нефтян. машиностр., 4, 12 (1972).

15. И. E. Идельчик. Справочник по гидравлическим сопротивлениям. – М.: Изд. «Машиностроение», 1975.

16. А. Г. Касаткин, Ю. И. Дытнерский, С. У. Умаров. Хим. пром., 3, 166 (1958). 17. В. В. Федоров. В сб.

«Новые идеи в планировании эксперимента». – М.: Изд. «Наука», 264 (1969). 18. В. А. Телитченко,

H. А. Цейтлин, Э. К. Беляев. Деп. ОНИИТЭХИМ (г. Черкассы), № 1561/78 (1978).

6.3.1.3. Метеорология. Математическое описание параметров климата Северного

Крыма, влияющих на процесс выпаривания солевого раствора в открытом бассейне

Граждане! Вступайте в ряды Фурье! (Первомайский плакат студентов 1979 г.)

В 1979 году профессор ХГУ Ю. В. Гандель (тогда ещё - простой доцент) посоветовал

автору взять на работу одну из лучших студенток выпуска Ирину Едвабник. «Не пожалеете», -

убеждал он. Действительно, Ирина Юльевна быстро освоила профессию аналитического

статистика и защитила диссертацию по довольно сложной теме - «Математическая модель

процесса выпаривания многокомпонентного раствора в открытом бассейне». Одна из её

публикаций (И. Ю. Едвабник // Статистические методы в основной химии: Труды. T. 63 /

НИОХИМ. – Харьков, 1986. - C. 97 - 103.), иллюстрирующая применение методов регрессионного

анализа (с оценкой дисперсии воспроизводимости откликов по данным почти параллельных

опытов и проверкой гипотез

-методом), представлена ниже.

Интересно, что прежде, чем начать данное исследование, мы обратились к

профессионалам. Однако климатологи не смогли предоставить ничего, кроме статистических

данных, и заявили, что создать математическую модель климата территории для нас,

дилетантов, - задача непосильная. Тем не менее, Ирине Юльевне не только удалось решить

«непосильную» задачу, но дополнительно сформулировать и подтвердить гипотезу о том, что с

введением в действие Северо-крымского канала климат Северного Крыма становится мягче!

В данной работе обобщены многолетние наблюдения работников метеостанции Ишунь.

Эмпирические зависимости параметров климата от времени года аппроксимированы с помощью

первых членов ряда Фурье.

При построении математической модели процесса выпаривания дистиллерной жидкости

содового завода в открытом бассейне [1] возникла необходимость в разработке элемента этой

модели, описывающего случайные колебания параметров климата.

Рассмотрим множества среднемесячных значений температуры воздуха t, °С, относительной

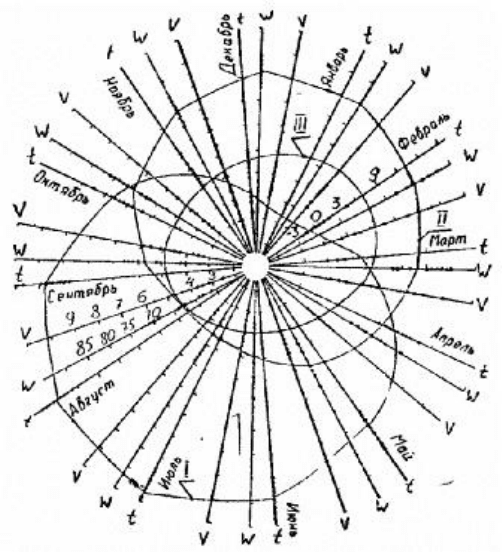
влажности воздуха W, %, средней скорости ветра V, м/с (рис. 1),

Рис. 1. Среднемесячные значения средней температуры воздуха t, °С; относительной

влажности воздуха W, %; средней скорости ветра V, м/с (в полярных координатах); I, II, III -

графики эмпирических функций регрессии (2), (3) и (4) соответственно.

а также суммарного количества осадков d, выпавших в течение месяца, мм (по данным

метеостанции, расположенной в поселке Ишунь Красноперекопского района; рис. 2).

Постулируем повторяемость метеоусловий, которая выражается в зависимости средних

значений параметров климата от времени в виде периодической функции

()

(

)

()

(

)

()

011011011

jjjj

MYcosujsinuj

ααταατββτ



=+++++



∑

, (1)

где M(·) - математическое ожидание случайной величины;

= (t, lgW, lgV, lgd)

- отклик

(вектор функций параметров климата);

- последние две цифры номера года (

∈

{78, 79, ..., 83});

u = 2π(τ

- 0,5)/12; τ

- номер месяца;

- векторы коэффициентов функций регрессии.

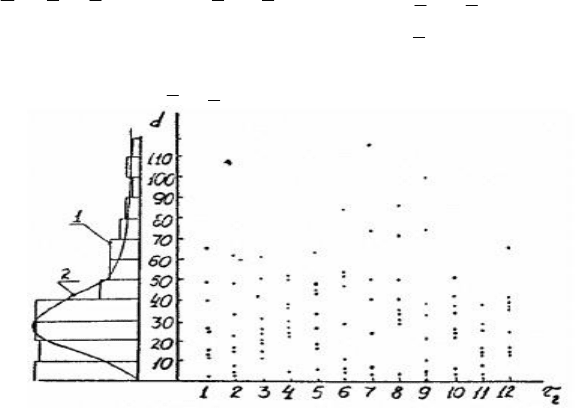
Рис. 2. Количество осадков, выпавших за каждый месяц в течение 1975 - 1983 гг.:

1 - эмпирическая плотность распределения количества осадков; 2 - ее аппроксимация

по формуле (10); d - количество осадков, мм/мес.; τ

- номер месяца.

Заданная структура аппроксимирующей функции отражает сезонные изменения значений

параметров климата с периодом Т = 12 мес., а также линейный тренд по годам (изменение

среднего значения и амплитуд сезонных колебаний в период 1975 - 1983 гг.).

Так как параметры климата W, V, d принимают только положительные значения, то можно

предположить, что распределение логарифмов этих величин ближе к нормальному, чем

распределение натуральных величин. По среднемесячным метеорологическим данным (см рис. 1,

2), полученным в период 1975 - 1983 гг., оценены параметры эмпирических функций регрессии

типа (1):

t = 10,55 – 11,14cosu - 0,046τ

sinu; (2)

lgW = 1,8679 + 0,011sinu + 0,069cosu; (3)

lgV = 1,483 - 0,01τ

+ 0,064соsu + 0,04058τ

sinи + 0,026sin2u; (4)

lgd = 1,32 + 0,0012

cos2u. (5)

Для проверки информационной способности регрессионных моделей в работе [2]

сформулирована гипотеза Н

общ oY

σσ

= (где

общ

- общая дисперсия отклика,

- дисперсия

случайной ошибки регрессионной модели) против альтернативной гипотезы Н

общ oY

σσ

> .

Распределение статистики

общ oY

IS/S

= , предложенной для проверки гипотезы Н

, не совпадает с

распределением Фишера, так как дисперсии

общ

взаимозависимы.

Сформулируем гипотезу об информационной способности иначе - как гипотезу Н'

равенстве нулю всех коэффициентов регрессии (против альтернативной гипотезы Н'

, о том, что не

все коэффициенты регрессии равны нулю) и используем для проверки Н'

статистику Фишера [3]:

(

)

(

)

(

)

(

)

222

10000

1111

g,f общ YY

FSNSf/gSJNf/g

−



=−−−=−−−







, (6)

где g - количество коэффициентов в уравнении регрессии; f

- число степеней свободы для

; f

= N - g; N - число наблюдений (N = 108);

общ oY

JS/S

= .

Следует отметить, что чем меньше оценка уровня значимости [3], тем с большей

ответственностью за выводы можно говорить об информационной способности соответствующей

функции регрессии.

С большой ответственностью за выводы [4] гипотеза H'

для уравнений (2) - (4) отклонена, а

для функции (5) не отклонена (см. таблицу), поэтому функция (5) для зависимости количества

осадков (мм), выпавших в течение месяца, от номера года и номера месяца аппроксимирована

средним арифметическим результатов наблюдений

d = 32,3 мм. (7)

Гипотезы о согласии распределения остатков эмпирических функций регрессии (2) - (4) и

нормального распределения не отклоняются по

-критерию [5] на уровнях значимости

> 0,1

(см. таблицу).

Таблица.

Статистические характеристики элементов математической модели климата Северного Крыма

Отклик Y

Показатель

t lgW lgV lgd

Среднее значение отклика

10,6 1,867 0,671 1,32

Среднеквадратичное отклонение (СО) отклика

8,5 0,055 0,108 0,53

СО остаточной ошибки модели

1,94 0,024 0,089 0,53

СО ошибки воспроизводимости отклика

1,94 0,026 0,024 0,52

Число степеней свободы

96 96 7 96

Коэффициент множественной детерминации R

0,96 0,79 0,35 0,02

Уровень

значимости

критерия

информационной способности

согласия по ω

-критерию

адекватности

0,0005

0,29

0,45

0,0005

0,12

0,7

0,0005

0,71

0,008

0,37

0,009

0,45

Генерирование случайной величины х, распределенной по нормальному закону с

параметрами N(0, 1), производят по формуле [6]

=−

∑

, (8)

где R

- независимые случайные величины, равномерно распределенные на интервале (0, 1).

Генерирование случайных величин t, lgW, lgV осуществляется по формуле

Y = S

x + M(Y). (9)

Гипотеза о согласии распределения случайной величины lgd и нормального распределения

отклонена на уровне значимости

= 0,009, поэтому для аппроксимации функции распределения

величины lgd можно воспользоваться распределением Пирсона [7].

Обозначим

- выборочный r-й центральный момент распределения случайной величины.

Поскольку коэффициент асимметрии

132

ˆˆ

βµµ

= = 4,218 > 0, коэффициент эксцесса

242

ˆˆ

βµµ

= 9,03 > 0, а определяющий параметр распределения Пирсона

(

)

(

)

(

)

122121

3423643

ˆˆˆˆˆˆ

ββββββ



=+−−−



= -10,92 < 0,

то эмпирическое распределение логарифма количества осадков соответствует

распределению Пирсона первого типа - бета-распределению.

Плотность распределения величины lgd имеет вид

f(x) = x

v-1

(1 - x)

w-1

/B(v, w), (10)

где B(v, w) - бета-функция, задаваемая формулой

()()

Bv,wuudu

−

=−

∫

Параметры бета-распределения v, w случайной величины Y оценивают по формуле [8]:

(

)

{

}

vYYY/µ



=−−



; (11)

(

)

(

)

{

}

111

wYYY/µ



=−−−



, (12)

где

- оценка математического ожидания случайной величины Y. Для величины Y = lgd

параметры бета-распределения v и w соответственно равны 1,1 и 0,46. Графический анализ (см.

рис. 2) показал, что эмпирическое распределение величины lgd хорошо согласуется с

распределением Пирсона первого типа. Генерирование случайной величины Y, имеющей бета-

распределение с параметрами v, w, осуществляется по формуле [6]

Y = S

/(S

+ S

), (13)

где S

; S

+ S

≤ 1; R

, R

- независимы и распределены равномерно на интервале

(0, 1).

Так как гипотезы о нормальности распределения величин t, lgW, lgV не отклонены, проверка

гипотез об адекватности моделей (2) - (4) осуществляется по критерию Фишера [3]. Ввиду

отсутствия параллельных опытов дисперсии воспроизводимости откликов оценивали по данным

почти параллельных опытов [8] (см. таблицу).

Гипотезы об адекватности моделей (2) и (3) не отклонены с обычной ответственностью за

выводы на уровнях значимости

()

= 0,45;

()

= 0,7.

Гипотеза об адекватности модели (4) не отклонена с малой ответственностью за выводы на

уровне значимости

()

= 0,008. Этот факт, а также структура формулы (4) (коэффициент α

≠ 0, то

есть имеется зависимость среднего значения скорости ветра от номера года) свидетельствует о

необходимости ежегодного уточнения формулы для расчета средней скорости ветра.

Для проверки качества прогнозирования значений параметров климата на 1984 г. по

формулам (2) и (3) сформулируем и проверим одновременно гипотезы о равенстве нулю

математического ожидания ошибки прогноза (Н

: v

= 0) и об однородности оценок дисперсии

прогноза

и остаточной дисперсии

(Н

σσ

= ) [9]. Гипотезы Н

и Н

для откликов t,

lgW не отклонены на уровнях значимости

= 0,1;

,lgW

= 0,055;

= 0,7;

,lgW

= 0,85 (первый

индекс оценки уровня значимости показывает номер проверяемой гипотезы, второй -

наименование отклика).

Построенная математическая модель параметров климата Северного Крыма, включающая в

себя формулы (2) - (4), (7) - (13), позволяет генерировать случайные изменения параметров

климата (то есть, параметры погоды) в имитационной модели процесса выпаривания

дистиллерной жидкости и других растворов в открытом бассейне, исследовать методом Монте-

Карло закон распределения параметров этого процесса, обеспечивает возможность выбора

оптимального режима выпаривания.

Литература

1. Едвабник И. Ю. Математическая модель процесса выпаривания многокомпонентного

раствора в открытом бассейне // Интенсификация технологических процессов и аппаратов

содового и смежных производств: Труды. - T. 60 / НИОХИМ. - Харьков, 1985. - С. 120 -

126.

2. Вознесенский В. А. Статистические методы планирования эксперимента в технико-

экономических исследованиях. - М.: Финансы и статистика, 1981. - 263 с.

3. Себер Дж. Линейный регрессионный анализ. – M.: Мир, 1980. - 456 с.

4. Самойленко В. И., Цейтлин H. А. Использование статистических методов при

исследовании процесса карбонизации гидроокиси магния, содержащейся в шламах

рассолоочистки // Технология соды и содопродуктов: Труды. - T. 52 / НИОХИМ. -

Харьков, 1980. - C. 9 - 17.

5. ГОСТ 11.006-74. Правила проверки согласия опытного распределения с

теоретическим. - M.: Изд-во стандартов, 1975. - 24 с.

6. Хастингс H., Пикок Дж. Справочник по статистическим распределениям. - M.:

Статистика, 1980. - 96 с.

7. Кендалл M. Дж., Стьюарт А. Теория распределений. - M.: Наука, 1966. - 588 с.

8. Цейтлин H. А., Гордеев Л. С., Ицков Ф. Э. и др. Адекватность эмпирической

функции регрессии данным пассивного эксперимента на промышленном о6ъекте // Тез.

докл. Всесоюз. науч. конф. "Повышение эффективности, совершенствование процессов и

аппаратов химических производств", Харьков, 11 - 13 июня 1985 г. - Харьков, 1985. - T. 7.

- С. 37 - 38.

9. Зайцев И. Д., Цейтлин H. А., Чайка В. П. Статистический анализ методов расчета

параметров физико-химических свойств многокомпонентных растворов электролитов

//Хим. пром-сть.- 1983.- № 8.- С. 500-503.

6.3.2. Исследование влияния одного важного фактора на отклик в пассивном

многофакторном регрессионном эксперименте

В практике регрессионного анализа результатов наблюдений неуправляемых объектов

иногда возникает

задача

определения влияния только одного важного фактора на отклик

Для решения этой задачи исследователи нередко наблюдают всего две выбранные для изучения

переменные и пытаются построить регрессию одной из них (отклика) на другую (фактор)

или даже просто рассматривают коэффициент парной корреляции между этими

переменными. На самом деле на отклик может влиять много других существенных факторов и

игнорирование их влияния приводит к грубым ошибкам. Необходимо учитывать влияние

существенных факторов путём их фиксации (для дальнейшего учёта в регрессионной модели). В

нашей практике встретились две подобные задачи. Одна - из области физиологии, вторая –

химико-технологическая. Опишем обе задачи полностью.

6.3.2.1. Биология. Регрессионный анализ связи инсулина в плазме крови с молочной

продуктивностью крупного рогатого скота

В споре не всегда побеждает истина, чаще это делают более тяжелые аргументы. (Софокл)

Одноимённая работа группы авторов (В. Н. Никитин, В. Е. Недава, Л. Л. Симиренко,

Н. А. Цейтлин, М. К. Асадова), выполненная на производственной базе Научно-

исследовательского Института Биологии Харьковского Государственного Университета в

семидесятых годах двадцатого века, после своего завершения была подготовлена к публикации,

но так и не увидела свет. Причина этого заключалась в многолетнем принципиальном

разногласии между авторами и рецензентом по вопросу определения направления влияния одного

из важных факторов (инсулина) на отклик (месячный удой) в ситуации, когда на тот же

отклик влияют другие значимые факторы.

В настоящем разделе описана попытка авторов обосновать свои взгляды путём

корректного использования многомерных статистических анализов (корреляционного и

регрессионного), а также содержательного анализа полученных формул.

К сожалению, оптимально планировать эксперименты в биологических исследованиях удаётся

редко и данная работа – не исключение. Однако при планировании сбора результатов

«пассивных» наблюдений всё же можно использовать принцип подбора существенно разных

объектов. Например, в данной работе при исследовании влияния инсулина, возраста, стадии

лактации и сезона года на месячный удой для наблюдений брали животных существенно разных

по возрасту, стадии лактации и сезону года (выбирать животных по различиям в содержании

инсулина не представлялось возможным).

Внимательный читатель сможет заметить различие ряда терминов и обозначений

переменных, принятых в практической биометрии и математической статистике. В биометрии

используется термин «достоверность» (вместо термина «значимость»); выборочные значения

средней величины, среднеквадратичного отклонения и уровень значимости обозначаются

буквами М, σ и Р, соответственно (без «крышечек», обозначающих статистические оценки,

индексов и прочих математических «тонкостей»).

С другой стороны, биологам (и медикам) надо отдать должное: они обычно любое

утверждение относительно проверяемых гипотез подкрепляют указанием уровней значимости

(правда, в приближённом виде – в форме неравенств).

Для научных основ племенного и продуктивного отбора животных в современной

зоотехнии наряду с показателями экстерьера при определении потенциальной продуктивности и

наследственных свойств животных все большее значение приобретают показатели интерьера и, в

первую очередь, эндокринные. Для прогнозирования молочной и мясной продуктивности

крупного рогатого скота особый интерес представляет выявление характерного для каждого из

них эндокринного спектра крови. Как для большого биохимизма лактации (биохимизма

приспособления к молочной продуктивности целого организма), так и для малого биохимизма

(собственно биохимизма молочной железы) наибольшее значение, по современным данным,

имеют инсулин, тироксин, кортикостероиды и пролактин [1 - 4]. Нами для исследования был

избран инсулин как почти универсальный гормон биосинтеза углеводов, жиров, белков и

нуклеиновых кислот. Инсулин, по последним данным, играет существенную роль в регуляции, по

крайней мере, 22 – х важнейших звеньев биосинтетических процессов [5, 6]. Необходимость

инсулина для регуляции развития и функциональной активности секреторного эпителия молочной

железы жвачных показана в условиях in vitro у коз [3] и коров [7]. Значительная зависимость

уровня секреции молочной железы жвачных от инсулина установлена при выключении функции

поджелудочной железы в условиях аллоксанового диабета. Дефицит эндогенного инсулина в

течение пятидневного диабета снижает у коз общий удой (с 987 до 55 мл), резко снижает

образование всех компонентов молока (суточной продукции лактозы - на 97, жира - на 80, казеина

- на 85%) [8].

У лактирующих жвачных выявлено рефлекторное влияние молочной железы на секрецию

инсулина. Стимулы сосания и доения повышают уровень инсулина в крови коз [9]. В некоторых

исследованиях найдено увеличение избирательной поглощаемости инсулина тканью молочной

железы в процессе лактации [10]. Такая стимуляция инсулярной функции поджелудочной железы

приводит к изменению направленности межсуточного углеводно-жирового обмена в организме

жвачных. При введении оптимальных доз инсулина лактирующим коровам и козам стимулируется

секреция молока и его основных компонентов [2, 10 - 12]. Определенную роль в этой стимуляции

может играть повышенное выделение пищеварительной системой в кровь сывороточных белков и

мочевины [12] и увеличение поглощения молочной железой из крови общих, связанных и

свободных углеводов [10], всех классов глобулинов и общего белка вцелом [11]. Перечисленные

исследования подтверждают представление о положительной связи инсулярной функции

поджелудочной железы с уровнем молочной продуктивности жвачных.

Следует, однако, учесть, что введение слишком высоких доз инсулина может отрицательно

сказаться на уровне молочной продуктивности коров [2]. Имеются также данные о том, что при

чрезмерно высоком содержании концентратов в рационе КРС молочная продуктивность несколько

снижается; было высказано предположение, что усиление выброса инсулина в кровоток

стимулирует в этих условиях преимущественное отложение липидов в жировой ткани [13]. В

одном из исследований [14] вообще не было установлено влияние инсулина на молочную

продуктивность жвачных животных (овец).

Ввиду неоднозначности имеющихся данных желательно исследование характера связи

между молочной продуктивностью и уровнем инсулина в крови в условиях физиологической

нормы, стандартных рационов, при взятии крови в оптимальные сроки и с учетом возрастных,

сезонных и породных особенностей.

В настоящей работе представлены результаты исследования количественной связи

концентрации иммунореактивного инсулина (ИРИ) в плазме крови коров разного возраста и

породы с уровнем их молочной продуктивности.

Методика

На протяжении 1976 - 1977 гг. обследовали 297 коров молочной черно-пестрой (n=141),

мясо-молочной симментальской (n = 102) пород и помеси джерсеи × симменталы (n = 54) стада

опытного хозяйства Терезино Украинского научно-исследовательского института разведения и

искусственного осеменения сельскохозяйственных животных.

Пробы крови отбирали у каждого животного дважды в течение часа, от 3 ч 00 мин до 4 ч 30

мин утра, до дойки и кормления. В этот период суток концентрация ИРИ в плазме крови

животных является наиболее стабильной [15, 16]. Образцы плазмы крови получали не позднее,

чем через 15 мин после взятия крови и сохраняли в жидком азоте. Концентрацию инсулина

определяли радиоиммунологическим методом с помощью наборов insir-1 фирмы CEA-IRE-

SORIN.

О молочной продуктивности коров судили по величине месячного удоя на 2-м и 8-м месяцах

лактации и по суммарному удою за первые три месяца лактации. Этот показатель коррелирует с

удоем за 305 дней лактации и рекомендован для оценки уровня молочной продуктивности [17, 18].

Математическая обработка результатов наблюдений

Целью математической обработки было определение связи показателей молочной

продуктивности коров с концентрацией инсулина в плазме крови, возрастом, породой и сезоном

года. Представление об этой связи можно получить с помощью многомерного регрессионного

анализа [19]. Этот довольно сложный анализ сводится в конце концов к построению

регрессионной модели явления. Регрессионная модель состоит из двух частей - регрессионной

функции (РФ) и случайной ошибки. Обработка наблюдений сводится к следующим действиям.

Выбирают зависимые переменные (отклики) и независимые переменные (факторы). Неформально

используя рациональные соображения, формируют структуру РФ с неизвестными

коэффициентами. Затем, по стандартной программе регрессионного анализа [20], на ЭВМ

обрабатывают весь многомерный массив наблюдений и получают эмпирическую функцию

регрессии (ЭФР). Программа позволяет проверить непротиворечивость экспериментальных

данных составленной регрессионной модели. В процессе регрессионного анализа факторы,

влияние которых на отклик не достоверно, исключаются из РФ (о достоверности влияния

факторов судят по достоверности отличия от нуля стоящих перед ними коэффициентов

регрессии). Таким образом, выполняется свертка РФ. Результатом расчета является ЭФР,

содержащая достоверные коэффициенты регрессии. Если парные коэффициенты корреляции

между оставшимися в модели факторами не достоверны, модель полностью пригодна для

интерпретации. В противном случае интерпретация модели является приближенной [21] (причём,

тем менее корректной, чем сильнее коррелируют между собой соответствующие факторы).

В нашем исследовании в качестве откликов приняты показатели молочной продуктивности -

удой за второй или восьмой месяцы лактации (D, кг) и удой за три первых месяца лактации (B, кг).

Независимыми переменными были: концентрация иммунореактивного инсулина в плазме крови

(И, мкед/мл), возраст животных (τ, годы), стадия лактации (x, месяцы) и сезон года (Θ, месяцы).

Последние три величины входили в регрессионную модель в виде аргументов нелинейных

базисных функций. Учитывая неравномерность изменений биологических показателей в

онтогенезе, использовали логарифм возраста (lgτ ). Из предварительных графических построений

было видно, что показатели молочной продуктивности коров в возрасте от двух до пяти лет резко

возрастают, а затем с возрастом плавно убывают. Эти изменения можно описать параболой

второго порядка и, значит, кроме функции lgτ, следует включить в РФ ее квадрат (lgτ)

Предполагая сезонную изменчивость (с периодом 12 месяцев) уровня молочной продуктивности и

концентрации ИРИ в плазме крови, ввели факторы, характеризующие эти колебания – члены ряда

Фурье: sin(2πΘ/12) и cos(2πΘ/12). Кроме того, учитывали эффекты взаимодействия [21] некоторых

факторов: Иlgτ, Иx, xlgτ. В качестве факторов, учитывающих «качественную» характеристику

животного - породу - использовали, согласно рекомендации [19, с. 143], кодовые переменные (Z

): черно-пестрая порода - Z

= 1; Z

= 0; симментальская порода Z

= 0; Z

= 1, помеси джерсеи ×

симменталы - Z

= 0; Z

= 0. Отметим, что этот прием позволил объединить экспериментальные

данные по трем разным породам в одну совокупность. Таким образом, для анализа постулирована

регрессионная модель следующего вида

= β

+ β

lgτ + β

(lgτ)

+ β

И + β

x + β

Иlgτ + β

Иx + β

xlgτ +

+ β

10i

sin(2πΘ/12) + β

11i

cos(2πΘ/12) + ε (1)

где Y

– отклики (Y

= D; Y

= В); β

– коэффициенты регрессии, ε – случайная нормальная

ошибка модели со средним значением, равным нулю и дисперсией

. На первом

предварительном этапе статистической обработки вычисляли средние (М), среднеквадратические

отклонения (σ) и корреляционную матрицу факторов (таблица).

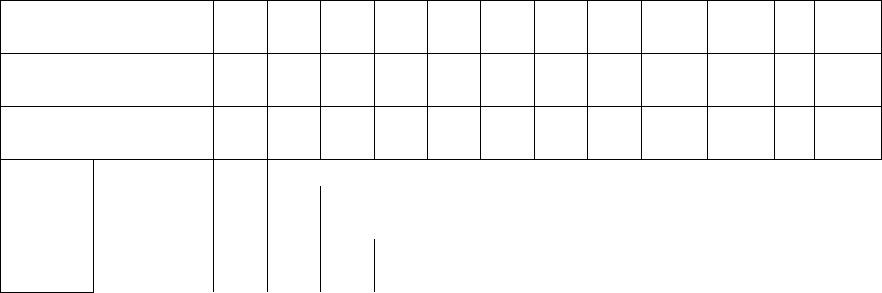
Таблица

Предварительная статистическая обработка показателей молочной продуктивности коров

Обозначения Z

Д τ В

(10

τ)

lg(10τ

)

(10τ

)

Иx

(10τ)

Среднее (М) 0,44

0,4

4,5

16,

5,3 1823

1,6

2,84 27,3 88

7,9

СО

(σ)

0,50

0,7

2,9 4,6 20

3,7 42

0,20

0,70 9,05

5,28

-0,48

T -0,02

0,0

Коэф

фици

енты

пар-

ной

корре

ляции

И -0,03

0,0

0,83