Черненко В.Д. Высшая математика в примерах и задачах (том 1)
Подождите немного. Документ загружается.


230 Г пава 6
2.
Ассоциативность (сочетательность)
АА{ВАС)
=
{ААВ)АС\
AV{BVC)
=
{AVB)VC.
3.
Дистрибутивность (распределительность)
AA{BVC)
= {AAB)V{AAC); AW{B AC) = {AV B)A{AVC).
2.1.
Используя логическую символику, записать утвержде-
ние:«число а есть точная верхняя грань множества X».
Решение. То, что число а есть точная верхняя грань множе-
ства X, записывается а
=
sup X и означает Ухе Х[х<а), при-
чем для сколь угодно малого £ справедливо условие
\/£>03хе X (х>а-'£).
63. Понятие о функции
р.
Если каждому значению одной переменной х по некото-
рому правилу ставится в соответствие определенное значение
другой переменной;;, то говорят, что между переменными суще-
ствует функциональная зависимость>^ =/(^)-
Переменную х называют независимой переменной или ар-
гументом,
г,
у — функцией. Функция может задаваться анали-
тически, графически и таблично.
Если функция задана уравнением, неразрешенным относи-
тельно
;;,
то говорят, что функция задана неявно, и записывают
f{x,y) =
Q.
Если соответствующие друг другу значения xviy выраже-
ны через третью переменную (например /), называемую пара-
метром, то говорят, что функция задана параметрически, и
записывают
'^
=
/(0'
y =
(p{t).

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ 2^
Функция может быть задана также различными аналити-
ческими выражениями на разных участках, например функция
Дирихле
\х (^) -1? ^С'^и
X
рационально,
\х (•^) =
0^
если
X
иррационально
или «сигнум
X»
|sgnjc = l, еслил:>0;
sgn
X
=
-1,
если
X
< 0;
[sgnO
= 0.
2^.
Если каждому значению у ставится в соответствие одно
или несколько значений
х,
то этим определяется однозначная или
многозначная функция
х-ц>{у)^
которая называется обрат-
ной функцией для функции у = /(х). Так для функции
у:=^а'
обратной фунукцией будет х = log^ у. В этом случае обратная
функция является однозначной. Для функции у
=
х^ обратная
функция будет двухзначной х = ±^у .
Для обратных функций справедливы соотношения:
?>(/W)=^' f{(p{y))=y-
Пусть каждому значению переменной х ставится в соответ-
ствие определенное значение переменной и
=
(р(х), а каждому
уже определенному знчению и ставится в соответствие опреде-
ленное значение y
=
f{u), тогда соответствие между значения-
ми х и
j;
имеет вид y
=
f{(p{x)) и определяет у как слолсную
функцию от
X,
т. е. функцию от функции.
3°.
Функция
>»
=/(х) называется четной, если при измене-
нии знака аргумента на противоположный значение функции не
меняется, т.
е./(х)
=/(-
х).
График четной функции симметри-
чен относительно оси ординат.

232 Гпава 6
Функция называется нечетной, если при изменении знака
аргумента на противоположный численное значение функции не
меняется, а знак функции меняется на противоположный, т. е.
f (-x)
=
-f (х). График нечетной функции симметричен относи-
тельно начала координат.
Функция называется периодической, если существует
такое число /, называемое периодом функции, что значе-
ние функции не меняется при прибавлении или вычитании
этого числа к любому значению аргумента, т. е.
/(jc) = /(x + /) = /(x + 2/) =
...
= /(jc +
A:/),
где к — любое
целое положительное или отрицательное число. График пери-
одической функции повторяется через равные интервалы.
4°.
Областью определения
функции является совокупность
всех значений аргумента, при которых данное аналитическое
выражение имеет смысл.
5^.
Преобразование графиков при некоторых простейших
изменениях функции;; =/(х):
а) график функции;; -f{x-d) получается из исходного пе-
реносом всех точек на а единиц по оси абсцисс вправо, если а
положительно, и влево, если а отрицательно;
б) график функции;; -f{x)-^b получается из исходного пе-
реносом всех точек на b единиц по оси ординат вверх, если Ь
положительно, и вниз, если
Ъ
отрицательно;
в) график функции ;; = Af{x) {А > 0) получается из исход-
ного растяжением его вдоль оси ординат в А раз, если А> 1,3,
1
при А <1 сжатием в— раз, если же
У4
<
О,
то ординаты меняют
еще и знак;
г) график функции ;; =f(kx) {к
>
0) получается из исходно-
го при к>1 уменьшением абсцисс в к
раз,
а при к <\ увеличени-
1
ем абсцисс в т" раз, если же
А:
<
О,
то абсциссы меняют знак и
к
график функции симметричен относительно оси Оу,

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ 233
Последовательно выполняя рассмотренные сдвиги
и
дефор-
мации графика исходной фунцции, можно получить график и
функции более сложного вида f{x)
=
Af[k{x -a)]
+
b.
x — l
3.1.
Дана функция f(x)
=
2х^ -х^ + 3
.
Найти част-
х
+ 4
ное значение функции при х = 1,
Решение. Чтобы найти частное значение функции при х = 1,
достаточно это значение аргумента подставить вместо х. По-
лучим
1
+ 4
3.2. Дана функция f(x)
=
х^
+
log^
х -f sin —. Найти значе-
а
ние функции при х =а.
Решение. Подставляем вместо х ее частное значение
f(a) =
а^
+
log^
а +
sin
— =
а^
+\
а
3.3.
Функция задана параметрически
{
jc
= acos/,
y-bsint.
Требуется записать эту функцию в неявном виде.
Решение. Чтобы записать функцию в неявном виде, следу-
ет исключить параметр /. Возводя в квадрат
г 2 1 2
\х =а cos t,
[y^=b^sm4
и преобразуя, получим —j+тт
"^ ^ •
а b
3.4.
Построить графики функций:

234 Гпава 6
[х при х>0\
\х^ при х<0;
б) /(x) = Jo при 0<jc<2;
-2х + 4 при х>2.
Решение, а) Строим график функции для
jc
<
О
и для
л:
>
О
(рис.
6.1.).
б) Строим график функции последовательно для участков:
х<0;
0<х<2; х>2 (рис. 6.2.).
Рис. 6.1 Рис. 6.2
3.5.
Найти область определения следующих функций:
а) y
=
yll-ylu^; б)
3;
= lg(2-Vb^); в)
>;
= arcsin—^; г)
___! 1_ _-
Решение. а)Выражения под знаком радикала должны быть
неотрицательны, т. е. l + jc>0 и
1-VTHTJC
>О• Отсюда д:>
—1
и
Vr+jc <
1;
1
+
JC<
1;
X
< 0. Следовательно, хе [-1,0].

ВВЕПЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАПИЗ 235
б) Выражение под знаком логарифма должно быть больше
нуля, т. е. 2-л/1-х>0; >/l-x<2;
1-х<4;
х>3 и выражение
под знаком квадратного корня
1
- х > 0; х < 1. Поскольку нера-
венства одновременно не могут быть выполнены, то
XG
0.
в) Выражение имеет смысл, когда -1 < <
1
и х
т^
3. От-
х-3
сюда
Г-х
+
3<1;
или
X
> 2;
X
> 4
.
Таким образом х
G
[4,
^о).
г) Выражение имеет смысл при х-1>0и5-х>0. Решая
эту систему неравенств, имеем х >1 и х < 5. Отсюда
XG
(1,5).
д) В силу свойств логарифмической и степенной функции
имеем следующую систему неравенств: sinx>0 и lgsinx>0.
Решением первого неравенства на периоде 2п является множе-
ство:
О
<
X
< л:, которое
с
учетом периодичности можно записать
в виде 2пк
<х<л{\
+
2к), ке z
,
Так как |sin
х|
< 1, то второму
неравенству удовлетворяет только равенство sin х =
1,
откуда
к
X
=
— +
2яА:.
Таким образом, область определения функции оп-
ределяется значениями х = —
(1
+
4А:),
ке z.
3.6. Путем деформации и сдвига графика исходной функ-
ции построить графики функций: а) j = 2sin(3x-2);
. 1 2 3 6х-1
Решение, а) За исходную функцию возьмем
j;
= sin х, а дан-
Г 9Л
ную функцию представим в виде
>;
=
2
sin 3
2
случае А =
2;
к = 3; а
=
—.
X— . В данном
3
236 Гпава 6
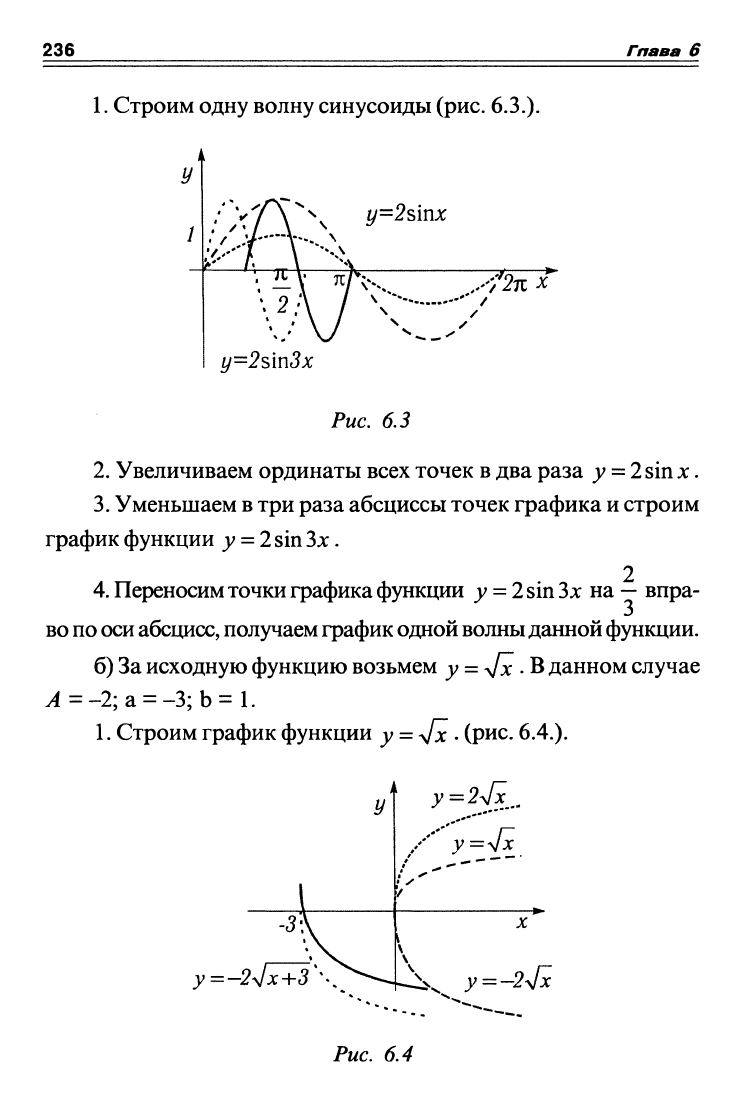
1.
Строим одну волну синусоиды
(рис.
6.3.).
i
у
1
^ r/=2sinA:
\*-*
» о Д / \ *- '' /
\ • \ / "^ /
,yf2n
X
* .^ _^
X
y-2sm3x
Рис. 6.3
2.
Увеличиваем ординаты всех точек в два раза
з^
=
2
sin jc.
3.
Уменьшаем в три раза абсциссы точек графика и строим
график функции
j;
=
2 sin
3JC.
2
4.
Переносим точки графика функции ;; =
2
sin Зх на
—
впра-
во по оси
абсцисс,
получаем график одной волны данной функции.
б) За исходную функцию возьмем у
= у[х . В
данном случае
У4 =-2; а =
-3;
b = 1.
1.
Строим график функции у =
у[х -
(рис. 6.4.).
у=-24х+3
Рис. 6.4

ВВЕПЕНИЕ В МАТЕМАТИЧЕСКИЙ АНАПИЗ
237
2.
Увеличивая ординаты в два раза, строим график функ-
ции у = 24х.
3.
Меняем знак на противоположный у = -2л/х
•
График этой
функции симметричен графику у =
2У[Х
относительно
оси
абсцисс.
4.
Переносим точки графика функции у = -2л/х на 3 еди-
ницы влево по оси абсцисс и строим график функции
7 = -2л/х7з .
5.
Поднимаем график функции
д;
= -2л/хТз на 1 вверх и
строим график данной функции.
в) Преобразуем данную функцию к виду
1
>;
= -(jc'-2jc
+
l)-2 = -(jc-ir-2.
За исходную функцию возьмем
j;
=
jc^.
В данном случае
^ = 2,^=1,6 = -2.
1.
Строим график исходной функции у^х^ (рнс. 6.5).
Рис. 6.5
2.
Уменьшаем ординаты графика функции
в
два раза
и
стро-
им график функции
j;
= — х^.

238
Гпава 6
3.
Сдвигаем по оси абсцисс на
1
единицу вправо точки гра-
1 \ 2
фика функции у=:—х^ и строим график функции
JV'
= — (^ -1) .
2 ^
4.
Опускаем точки графика функции на 2 единицы вниз и
строим график данной функции.
г) Преобразуем функцию к виду j =
3
-
10
2JC
+ 3
= 3-
х +
-
2
устанавливаем переход от функции j =
—
к заданной: —, —,
X XX
_^1
5_ 5_
х'
Ъ'^ 3-
JC
+
-
х + -
2 2
Выполняем следующие последовательные преобразования
(рис.
6.6): строим пока только одну ветвь гиперболы; растягива-
ем по оси Оу в пять раз; заменяем графиком, симметричным от-
носительно оси Ох\ строим вторую ветвь гиперболы; делаем
3
горизонтальный сдвиг координатной системы на
—
единицы
вправо и вертикальный сдвиг на
3
единицы вниз.
Рис. 6.6

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ 239
4х-9 9+2v
3.7. Показать, что функции у = и х = являют-
ся
взаимно обратными.
Решение. Подставим во вторую функцию вместо у его вы-
4х-9
ражение через х, тогда получим
(р
(/ (^)) = = х, Ана-
логично, подставляя в первую функцию вместо х его выражение
через у имеем /
((р
(j;)) = ^
=
у .
6.4. Вычисление пределов.
Раскрытие неопределенностей
1°.
Число b называется
пределом функции
f{x) при х
—>
а,
если для любого в >
О
найдется такое 5 > О, что |/(х)-б| < £
как только
|х —
а| < 5
.
Обозначают предел
lim/(x) =
Z>.
дг->а
Предел функции/(х), если он существует, при стремлении
X
к д справа обозначают lim f{x).
Аналогично, предел функции при стремлении х к а слева
обозначают
^^^^/{^).
2°.
Теоремы о пределах.
1.
Предел постоянной равен самой постоянной.
2.
Ит(м
+
v)
=
lim и
+
lim v.
3.
lim(w
v)
=
lim и
•
lim v,
,, и limu
4.
lim—= , если limi; 9^0.
V limu
