Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

250 Гпава

Решение этого примера можно найти

более простым

путем

а''-\

lim

3JC

= lim3

31п(3.

д) Делаем замену

tg^

= ^. При

д:

О ^

и предел при-

мет вид

lim(l +

2/V=Iim

/->0

2^)2/

е\

е) Делаем замену sin 2х =

При

л:

—> — ^

О. Пред-

ставим

tg^

2х =

sin'

2х

(1 +

Тогда

l-sin'2x

\-{\

lim

/->0

(1+0'

t{2

ж) Сделаем следующие преобразования

lim-

= lim

;г->0

in2jc

sinjc ^sinx

sin2jc-sinx

= lim

^sin. J^sin2.x-sin. ^

j (sin 2X - sin X)

jc(sin2x-sinjc)

,. sin2x--sinx

sin2x

sinx

= lim = lim

lim =

jc->0

X ^~^^ X ^^^ X

з) Воспользовавшись свойствами логарифмов, имеем

lim

x(]nx-ln(x + 2)) =

lim In

(

X ^

= lim

2) *^°°

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИИ АНАПИЗ

251

= In lim

+ - = In lim

+ - = lne-'=~2.

4.9. Найти пределы: a) lim

л:"'"'';

6) lim (In x)

x-^O

Решение, a) Неопределенность вида 0^. Обозначая функцию

под знаком предела за

и логарифмируя, будем иметь

sinx ,

= sm х

In JC

X In

Отсюда, на основании пункта

имеем

lim

= lim lim

x In

x = 0,

следовательно, limx"'""" =1.

6) Неопределеность вида

oo^.

Обозначая функцию под зна-

ком предела за

и логарифмируя, будем иметь

— In In

х .

Отсюда на основании пункта 4° имеем

,. , ,. In

In X In X

Iim

In ;;

= lim = 0,

следовательно, lim (Inx)^ =1.

(^'"'-l)sin3x

4.10. Найти пределы: a) lim—; -r-: r;

--^4n(l-3x')(l-cos2x)

6) lim

(Vl + sinx ~ 1 j arctg 3x

252 Гпава 6

Решение, а) Так как при х -->

О,

2х^

—>

О,

Зх

—>

О,

Зх

О,

и 2х ~>

О,

то имеем неопределенность -г. Заменяя

исходные бесконечно малые эквивалентными, получим

ie^""

-ljsin3x 2х^ -Зх

lim—7 7^"Т

li^

'л =

"~1

•

-oin(l-3x^)(l-cos2x) ^-'__^^г

li^2x)'

б) При х

—> О

имеем неопределенность вида --. Заменяем

исходные бесконечно малые эквивалентными и упрощаем

(VH-sinx~l)arctg3x -sinx-3x 3 3

lim-^--^ г = lim^^ = lim—cosx =—.

x^o

(e^sx-ljarcsin2x ^-^^ tgx-2x ^^M 4

6.5. Непрерывность и точки разрыва

функции

1°.

Если аргумент функции получает приращение

Ах

Х2

-Xj, то значение функции при новом значении аргумен-

та равно/(х +

Ах)

= 7 +

Ау.

Отсюда приращение функции

Ау = /(х +Ах)-/(х), т. е. приращение функции равно разно-

сти наращенного значения функции (при наращенном значении

аргумента) и начального значения функции.

Приращение аргумента может быть не только положитель-

ным, но и отрицательным числом.

2°.

Определение непрерывности функции:

Функция у

/(х) непрерывна в точке х

а, если пре-

делы слева и справа равны и равны значению функции в этой

точке, т. е.

lim f(x)= lim f(x) = f (а).

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ 253

Функция

y-f{x)

непрерывна в точке х

а, если она оп-

ределена в этой точке и если бесконечно малому приращению

аргумента соответствует бесконечно малое приращение функ-

ции, т. е. lim Ay =

вблизи точки а.

Ах->0

Сумма, разность

произведение конечного числа непрерыв-

ных функций есть функция непрерывная.

3°.

Непрерывная на отрезке

[а,Ь\

функция принимает любое

промежуточное значение между

ее

наименьшим т

наибольшим

М значением, то есть т

f{x)

М для всех jce {a,b]. Отсюда

следует, что если в граничных точках отрезка

[а,Ь]

функция име-

ет разные знаки, то внутри отрезка есть по крайней мере одно

такое значение х = с, при котором функция обращается в ноль.

Это свойство непрерывности функций позволяет находить при-

ближенно корни многочленов.

4^.

Значения аргумента, которые не удовлетворяют услови-

ям непрерывности, называются точками разрыва функции. При

этом различают два рода точек разрыва функции.

Если при х^> а слева функция имеет конечный предел к^,

а при

X —>

flf

справа функция имеет конечный предел ^2 и

А:,

=?^

А:2,

то говорят, что функция при X - а имеет разрыв

первого

рода.

Разность

\к^

к^

определяет скачок функции в точке х

а. Зна-

чение функции при X =а при этом может быть равно какому

угодно числу к^.

Если значение функции при х

а равно

к^,

то говорят, что

функция непрерывна слева; если же к^, то говорят, что функция

непрерывна справа.

Если

A:i

/^2

^3'

^^ говорят, что функция имеет в точке а

устранимый разрыв.

Если при Х'-^а справа или слева, предел функции не суще-

ствует или равен бесконечности, то есть liJTi/(x) =

«^,

то гово-

рят, что при X

а функция имеет разрыв

второго

рода.

254

Гпава

5.1.

Найти приращение функции у =

2х^

-3JC

если аргу-

мент

л:

изменился от х^ =

до ^2 = 2.

Решение. Найдем приращение аргумента

= X2-Xj =2-1 =

Вычислим исходное значение функции

j;(x,)

2-1^-3-1

= 0. Вычислим новое значение функции

XJCJ+AX)

= X1 +

2-2'-3-2

11.

Отсюда приращение функции Ау =

у{х^

Ах)

- у{х^) =

11.

5.2.

Найти приращение функции у

Ъх^

-2х + 4 и вычис-

лить его при

= 2 и Ах =

-0,1.

Решение. Новому значению аргумента х

+ Ах

соответству-

ет

новое значение функции

j;(x

Ax)

= 3(x

+ Ах)

(х +

Ах)

+ 4.

Приращение функции равно Ау =

j^(x

+ Ax)->'(x) =

= 3(х + Ах)^-2(х

+ Ах) +

4-Зх^-2х-4

(ЗАх +

6х-2)Ах.

Прих =2и

Ах

= -0,1 получим

Ау;

(-0,3+12-2)(-ОД)

= 0,97.

5.3.

Найти множество значений х, при которых функция

у =

х^

- 2х непрерывна.

Решение. Найдем приращение функции

Ау

= (х+Ах)^-2(х+Ах)-(х^-2х) = Ах(АхЧЗхАх

Зх^-2).

При любых значениях х приращение Ау

—>

О, если только

д^

О 5

поэтому функция непрерывна при всех действительных

значениях х.

5.4.

Доказать непрерывность функции у =

точке х = 3.

х-1

Решение. Для доказательства найдем приращение функции

у при переходе значения аргумента от х = 3 к х =

Ах

1 1 ^ 1

1^2-2-Ах_

-Ах

•^"'з +

Ах-1

3-1^2 +Ах 2"2(2 + Ах)"2(2 + Ах)'

Найдем предел приращения функции при Ах

—> О

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ

255

lim Ay = - lim

—

= 0.

Так как предел приращения функции при Ах ->

равен

нулю,

то функция при х-Ъ непрерывна.

5.5.

Найти

хотя бы один корень уравнения

Зх^

2х^

- х -1 = 0.

Решение. Найдем точку пресечения графика функции

у-Ъх'-\г

2х^ -

-1 =

с осью Ох, то есть точку, в которой у = 0.

Подберем две произвольные точки, в которых функция имеет

разные знаки. Пусть х =

О,

тогда у =

-1,

у < 0. При х = 1,

у =

+ 2-1-1 =

у>0. Значит корень находится между

л:

и х =

(в силу свойства непрерывности).

Определим знак функции в середине промежутка

[0,1],

т. е.

прих =0,5.

Находим

з;

= 30,5Ч20,5^-0,5-1 = -0,625; ;;<0. Зна-

чит корень находится между х = 0,5 и х = 1.

Определим знак функции в середине этого промежутка, т.

е. при

—.

Находим

—

Следовательно, корень находится внутри промежутка

1 1

2'4

. Находим знак функции в середине этого промежутка, т.

е.приД^--,

= 3 -

1 ^

2'8

Значит корень находится внутри промежутка

Можно уже считать, что ^ - -т

•

Если требуется большая точ-

ность, то указанный процесс приближений может быть про-

должен дальше.

256

Гпава

5.6. Определить характер разрыва

функций:

а) у

^Р^

х-1

X \2х при х^2

х = 1; б)

У =

1Г\

прих=0;в) у^\

\х\ [1 при х = 2\

г) у^а"" (а >

1);

д) у

arctg ~ и построить графики

Решение, а) При х = 1 функция не определена:

lim

кция имеет разрыв второго рода (рис. 6.7)

+«^.

Следовательно, при х =

фун-

Рис, 6.7

б) При

д:

предел равен lim — = -1 =

/:^..

При х >

пре-

дс-^1-0 \х\

дел равен lim т-г =

^2-

•

Следовательно, при х =

функция

имеет разрыв первого рода и скачок функции равен

к-^2|

= И-1| = 2(рис.6.8).

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ 257

у'

-1

Рис. 6.8

в) Функция определена на всей числовой оси, неэлементар-

ная,

так как в точке

л:

= 2 аналитическое выражение функции

меняется.

Исследуем непрерывность функции в точке х = 2:

lim 2х = 4, lim 2х = 4, у(2) =

t=L:AL.

Очевидно, что

точке х =

функция имеет устранимый раз-

рыв (рис. 6.9).

Рис. 6.9

г) Найдем пределы:

д;(+0)= lima^ =-н«,

>'(-0)=

lima^ =0.

JC-4+0

jr->-0

258

Гпава 6

В точке

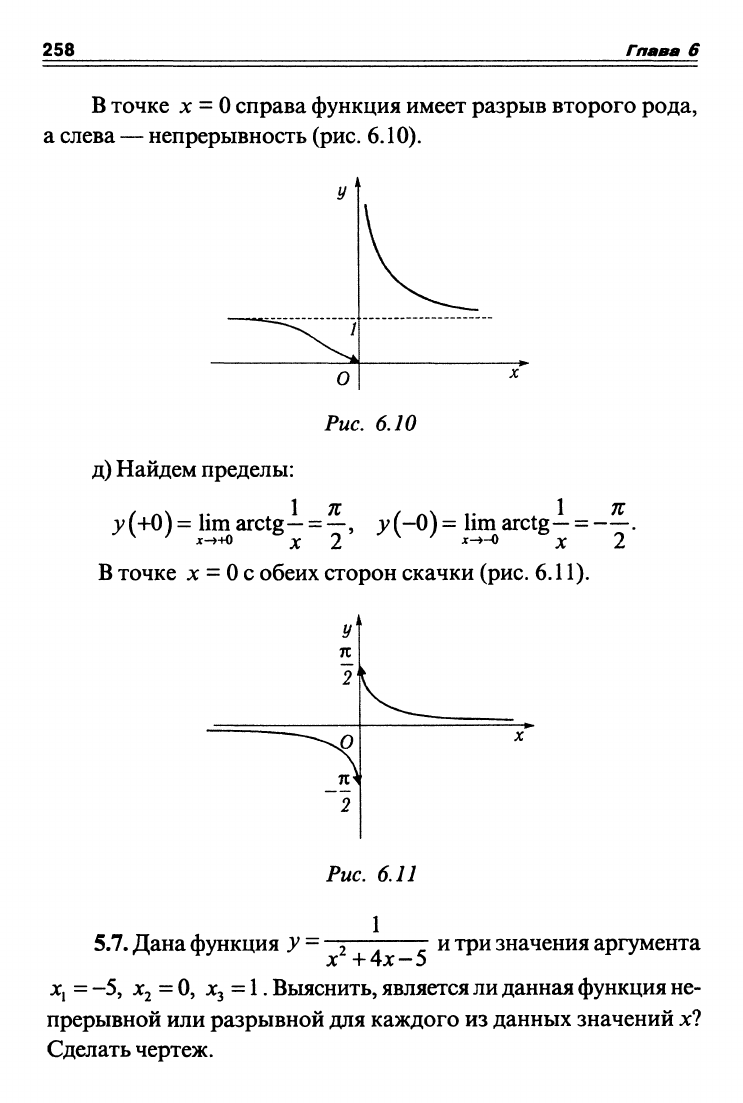
справа функция имеет разрыв второго рода,

а слева — непрерывность (рис. 6.10).

"^~~--х^^

Рис . 6.10

д) Найдем пределы:

>'H) = Ji^^^tg- = f'

>^(-0)

= ]imarctg-- = -|.

В точке

с обеих сторон скачки (рис. 6.11).

5.7.

Дана функция

Рис. 6,11

и три значения аргумента

jCj

-5,

^2 =

О,

лгз

Выяснить, является ли данная функция не-

прерывной или разрывной для каждого из данных значений х?

Сделать чертеж.

ВВЕПЕНИЕ

MA ТЕМА ТИЧЕСКИЙ АНАПИЗ

259

Решение. Исследуем непрерывность функции

точке

X = -5:

lim

-1,

lim

x-^-s-dx^

Л-Лх-Ъ

^-^-^^^х^

Л-Ах-5

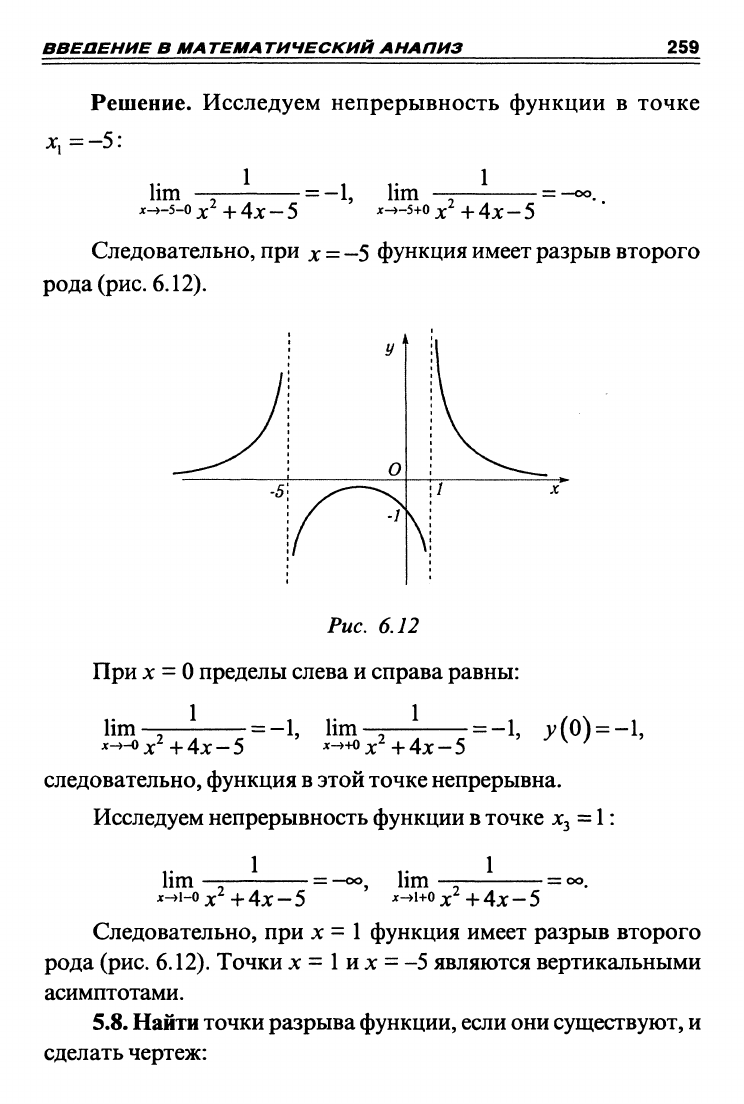
Следовательно, при

= -5 функция имеет разрыв второго

рода

(рис.

6.12).

Рис.

6.12

При

пределы слева и справа равны:

lim

-1,

lim

—1,

>;(0)=:-1,

^-^-ох^+4х--5

^-*-^х^+4х-5

следовательно, функция в этой точке непрерывна.

Исследуем непрерывность функции в точке

Хз

.. 1

lim

^-*»-ох +4х-5

lim

дс^1+0д;^+4х~5

Следовательно,

при х =

1 функция имеет разрыв второго

рода (рис. 6.12). Точки

х =

и х = -5

являются вертикальными

асимптотами.

5.8. Найти точки разрыва функции, если они существуют,

сделать чертеж: