Черненко В.Д. Высшая математика в примерах и задачах (том 1)

Подождите немного. Документ загружается.

260

Гпава 6

а) у=

jc^,

jc<l;

l<jc<3;

-х+5,

x>3;

б)

>^=]jcH

-i<jc<a,

jc>0.

Icosjc,

в) y =

3, jc = 0 w jc = ±3;

9-x\ 0<|x|<3; T) y^

9, IJCI > 3,

2x-l,

x<0;

^ x>0.

Х-Г

Решение, a) Функция неэлементарная, так как задана тре-

мя аналитическими выражениями на различных промежутках

изменения аргумента, определена на всем множестве действи-

тельных чисел.

Исследуем непрерывность функции в точках х =

и х = 3

j;(l)=

limx'=l; v(3) = l; lim (~х + 5) = 2 =

А:.

Таким образом, в точке х =

функция непрерывна, а в точ-

ке х =

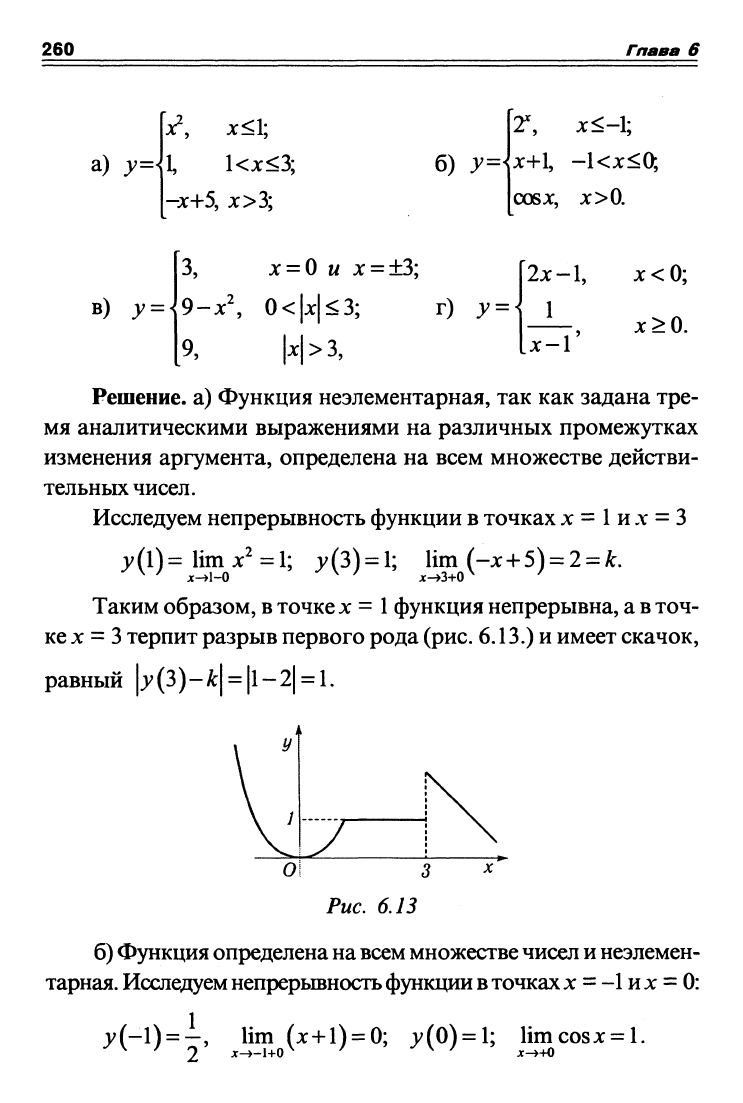
терпит разрыв первого рода

(рис.

6.13.)

и имеет скачок,

равный |j^(3)-A:| = |l~2| = l.

б)

Функция определена на

всем

множестве чисел и неэлемен-

тарная. Исследуем непрерьшность функции в точках х = -1 и х = 0:

v(-l) = -, lim (х

+ 1)

= 0: v(0) = l; limcosx = l.

ВВЕДЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ

261

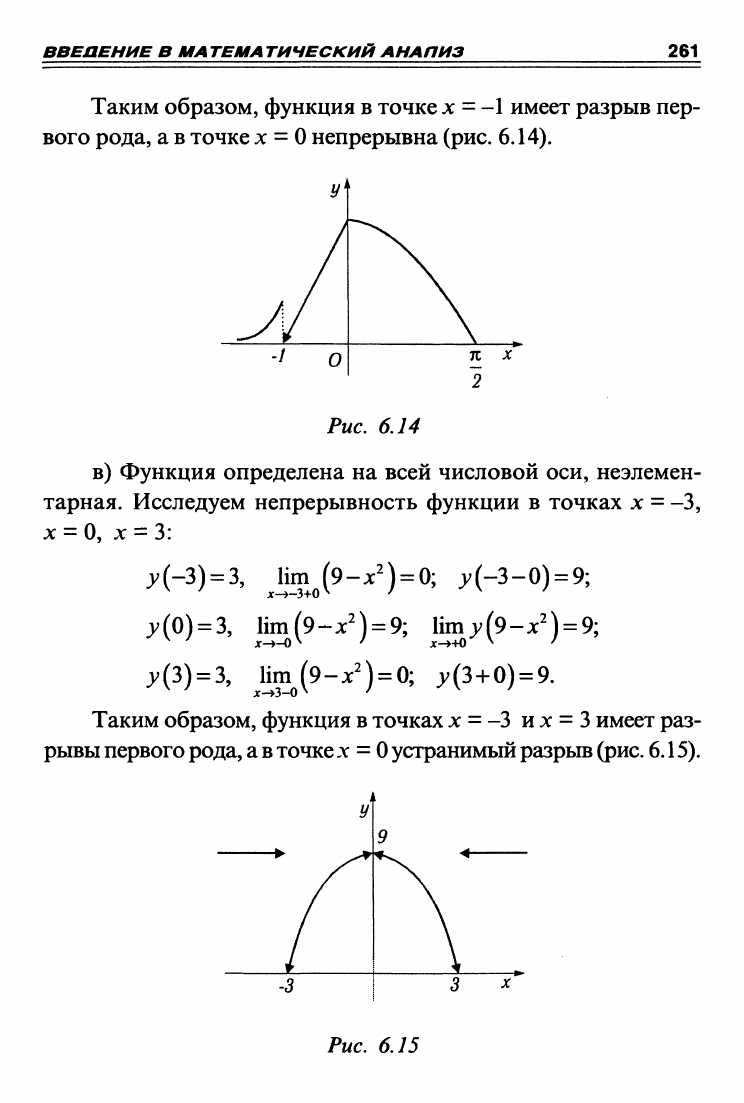
Таким образом, функция в точке

= -1 имеет разрыв пер-

вого рода, а в точке х =

непрерывна (рис. 6.14).

Fuc. 6.14

в) Функция определена на всей числовой оси, неэлемен-

тарная. Исследуем непрерывность функции в точках х - -3,

л:

= О,

= 3:

3;(-3)

lim (9-х^) =

j(-3-0) = 9;

>'(0) =

lim(9-xM =

Х\ту{<)-х^\

= %

>;(3) =

lim(9-jc') =

0; ;;(3

+ 0) = 9.

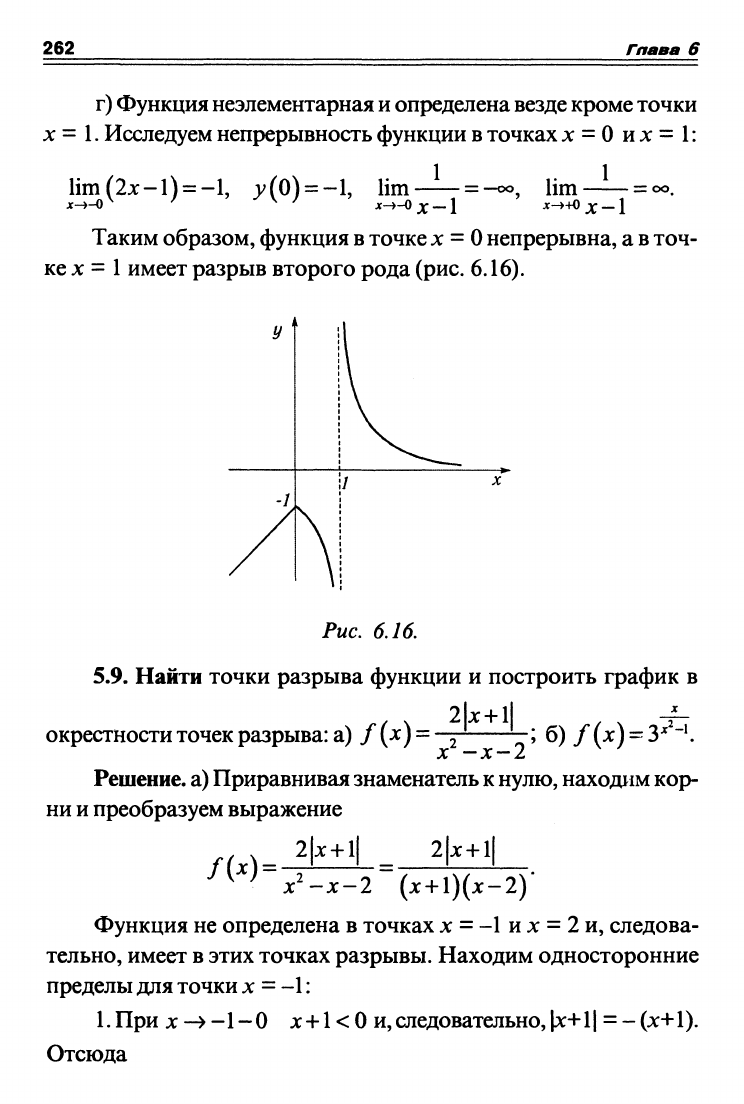
Таким образом, функция в точках х = -3 и х = 3 имеет раз-

рывы первого рода, а

точке х = О устранимый разрыв

(рис.

6.15).

-5

i 3 ^

Рис. 6.15

262

Г пава 6

г) Функция

неэлементарная

определена

везде кроме

точки

Исследуем непрерывность функции

точках х =

О и

х = 1:

1 .. 1

lim(2x-l)

-l, >'(0)

-1,

lim

Таким образом, функция

точке х =

непрерывна, а

точ-

ке

х =

имеет разрыв второго рода

(рис.

6.16).

Рис. 6,16.

5.9. Найти точки разрыва функции и построить график в

окрестности точек

разрыва:

а) / (х) =

2х

+ 1

х'-х-2

;б)/(х) = З^Ч

Решение,

а)

Приравнивая знаменатель

нулю,

находим

кор-

ни и

преобразуем выражение

2U+1I

/С

. 2|x-fl| 2|x

х^-х-2

(х +

1)(х-2)

Функция не определена в точках х = -1

х = 2 и, следова-

тельно, имеет

этих точках разрывы. Находим односторонние

пределы

для

точки

-1:

1.При

х-^-1-0

1<0 и,следовательно,|х+1| = ~(х+1).

Отсюда

ВВЕПЕНИЕ В MA ТЕМА ТИЧЕСКИЙ АНАПИЗ

263

/(-1-0)= lim —fei^

= ~2

lim -^

•^

/ ^-^-i-o(jc

l)(jc~2) x->-i-ojc~2 3

2.При

х->-1

+ 0

l>О,значит|х+1|

х+1

/(-l

0)=lim-ii^l^ = 2

lim

^-^-i+o(jc-f-l)(jc-2) д^->-1+од:-2 3

Поскольку оба предела конечны

не

равны,

то

точка х = -1

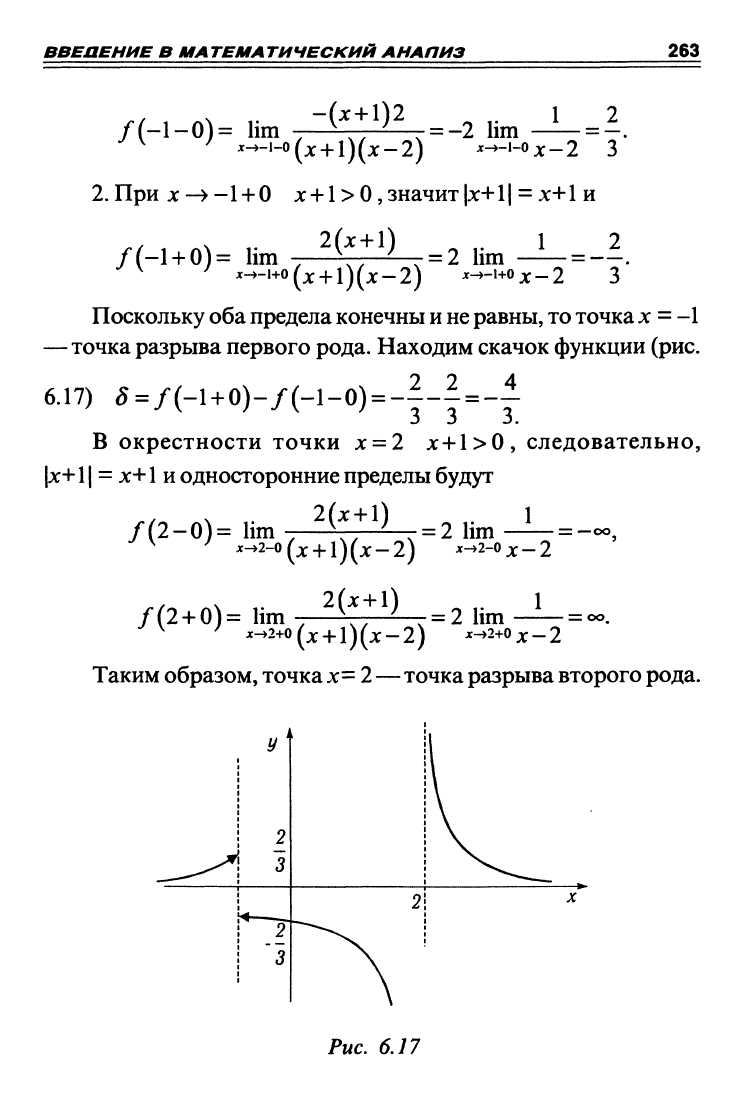
— точка разрыва первого рода. Находим скачок функции (рис.

6.17) 5

/(-1 + 0)-/(-1-0) = -|-|

В окрестности точки х-2 д:+1>0, следовательно,

|х+1|

х+1 и

односторонние пределы будут

/(2-0)= lim

^(^

0 2 lim J-

-oo,

V f

-^2-о(д:

+ 1)(д:_2)

х^2-од:_2

/(2

0)= lim —Ifclll—=

lim -i-

oo.

*-*2+0(x + l)(x-2)

x-*2+0x-2

Таким образом, точка х-2—точка разрыва второго рода.

Рис. 6.17

264

Гпава 6

б) Данная показательная функция не определена в точках

= -1 и

л:

и, следовательно, имеет в этих точках разрывы.

Найдем односторонние пределы, учитывая, что а > 1, то есть

а! ^

ч-оо

при t ->=-н» и д'

—> О

при / -^ —^.

Для точких = -1 при jc^-l-O, ^ -1>0,

х^-\

<0 и

«^^-оо

Отсюда/М~0)= lim 3^-^=0.

Прих->~1 + 0, х'-1<0, -Д—>0и ^

х^-1

•^=00.

Следовательно, /(-1 + 0)= lim 3^'"^ =+оо.

jc-)-l+0

Таким образом, точках = -1 —точка разрыва второго рода.

Рассмотрим точку х = 1. Находим пределы

/(1-0)= lim 3^'-^ =0, /(1 + 0)= lim 3^

=+со.

функция в точке х =

имеет также разрыв второго рода.

Найдем теперь пределы при х -^ ±^

/(-оо)= lim

3^'-^

=1, /(«>)= lim

3^'-^

=1.

График функ-

ции показан на

рис.

6.18.

Рис. 6,18.

Глава 7

ДИФФЕРЕНЦИАЛЬНОЕ ИСЧИСЛЕНИЕ

ФУНКЦИИ ОДНОЙ ПЕРЕМЕННОЙ

7*1*

Вычисление производных

1°.

Производной

от функции у

f(x) в точке

называется

предел отношения приращения функции

приращению аргумента

Д^->о

Дх

^-^^

Ах

Если этот предел конечный, то функция называется диф-

ференцируемой в точке

Производная обычно обозначается

или

у'^,

или f\x), или

-7~.

Нахождение производной называется дифференцировани-

ах

ем

функции.

Частное значение производной при

=д обозначается f\ci)

или у\ .

Геометрически производная У(^о) функции j =/(х) пред-

ставляет угловой коэфициент k

X,ga

\XQ)

касательной к гра-

фику этой функции в точке х^ (рис. 7.1).

266

Гпава

Рис, 7,1

Числа /.Uo)= 1^^ —^— и /+(^о)= li^ —Г— назы-

ваются соответственно левой и правой производными функции

f[x) в точке

JCQ

Для существования производной функции

/(х) в точке

необходимо и достаточно, чтобы ее левая и

правая производные в этой точке существовали и были равны

между

собой:

/_' {х^) = // (х^).

Если существует (конечный или нет) предел lim /(х) = Л/,

ТО

такова же будет и производная в точке

JCQ

справа (слева).

Если

точке х^ производная

не

определена, но функция име-

АУ(^О)

ет различные односторонние пределы lim — и

lim

АУ(^О)

, то в этой точке графика функции существуют две

различные с соответствующими угловыми коэффициентами

к^.к^,

односторонние касательные, составляющие угол

(рис,

7.2.),

а точка называется угловой.

Если lim

Дх-^О Дх

±оо

то есть функция имеет бесконечную

производную, то она не дифференцируема в этой точке. В этом

аИффЕРЕНиИАПЬНОЕ ИСЧИСПЕНИЕ ФУНКЦИИ

267

случае график функции имеет вертикальную касательную

(точ-

ка

перегиба).

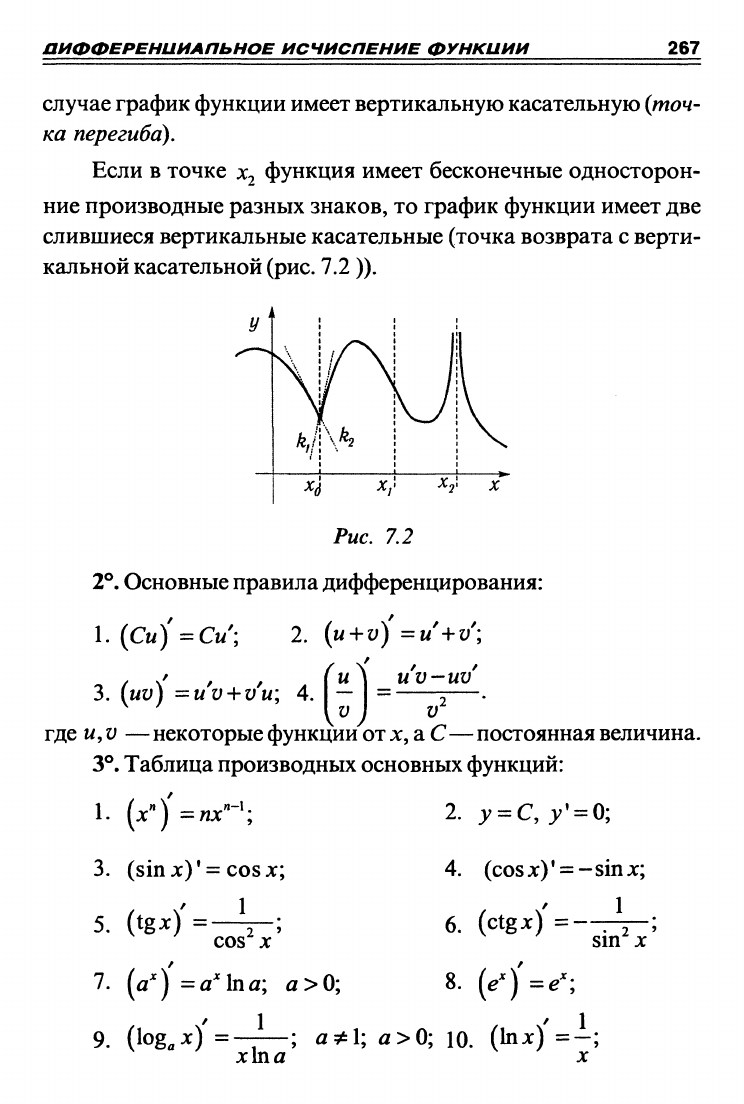
Если в точке ^2 функция имеет бесконечные односторон-

ние производные разных знаков, то график функции имеет две

слившиеся вертикальные касательные (точка возврата

верти-

кальной касательной

(рис.

7.2)).

х/> x^l X

Рис, 7,2

2°.

Основные правила дифференцирования:

{uv) =u'v

v'u;

uv-uv

где u,v — некоторые функции от

С—постоянная

величина.

3°.

Таблица производных основных функций:

(х"")

=^"-'1

у = С,у' =

3. (sinjc)* = cosx;

^ /"tirrV- ^ •

5. \ЩХ) - ,

cos JC

(cosjc)* = ~sinjc;

/1 {nicr V

—

6. vcigxj - . 2 '

Sin JC

(а')'=аЧпа; a>0;

8. (e')'=e^;

9. (log,x)'=——; a^l; a>0; 10. (1пх)'=-;

jclna д:

268

Гпава

И. (arcsinjc) = . ; 12. (arccosjc) =-

13.

(arctgx) =- -\ 14. (arcctgx) =-

+ x^' ^- ^ ^ ^ l + jc^'

15.

(shjc)' = chjc; 16.

(chA:)*

= shx;

17.

(thx/=-^; 18. (cthx/=--^

ch jc ' sh X

4^.

Гиперболический

синус,

косинус, тангенс и котангенс

определяются выражениями

e''-ё'''

e''+е'''

, shx , chx

shjc = ;

спл:

= ; thjc = ; cthjc =

2 2 chx shx

и обладают свойствами:

ch^x-sh^jc = l; 2. ch^x + sh^x = ch2x;

sh2jc = 2shjcchx; 4. shO = 0; chO = l.

5^.

Производная от сложной функции

j;=/(w),

где

(х),

равна произведению производной от этой функции по промежу-

точному аргументу

на производную от промежуточного аргу-

мента

по независимой переменной х, т. е.

1Л.

Пользуясь только определением производной, найти

производные от функций:

а) у=:х^-Зх +

6) у = 4х\ в)

= tg2x.

Решение, а) Находим приращение функции

Ay = ^(x

Ax)-;; = (jcH-Ax)^-3(x +

Ax) +

5-jc^+3x-5

X^+2XAX

AX^-3JC~3AA:4-5-X^+3JC-5

2JCAX

AX^-3AX.

По определению производной имеем

У= lim —= lim > = lim(2x--34-Ax) = 2x-3.

аИффЕРЕНиИАПЬНОЕ ИСЧИСЛЕНИЕ ФУНКЦИИ 269

б) Приращение функции

равно:

Ду =

VJC

- л/х.

По определению производной имеем:

у = lim -^ = lim =

д^->о

Дх

д«->о Дх

(л/л:+Ах-л/х)(л/х+Ас + л/х)

= lim

j-===L—-=гт

^-^^ Ax(Vx+Ax + Vx)

__ х +Ах-х _ 1 _ 1

^-^«Ах(л/х + Ах + >/^) ^-^^(л/х + Ах + л/]^) 2л/^'

в)

Находим приращение функции

A>;

= tg(2x + 2Ax)-tg2x =

sin

(2х+2Ах) cos 2х - sin 2х cos (2х+2Ах) sin (2Ах)

cos (2х+2Ас) cos 2х cos (2х+2Ах) cos 2х

По определению производной

, ,. sin (2 Ах)

у = lim ^

= lim

Д«-*о

Axcos (2х + 2 Ах) cos 2х

2 2

Д^-^о

cos (2х + 2Ax)cos2х cos^ 2х

1.2. Найти производные функций: а) >^= |х|, (х^^О);

б) >;=|2х-3|; в)

= e'W г) з;=и +

+ к-1|.

Решение, а) Представим функцию в виде

{

> 0;

-X,

х<0,

тогда

,^Г1,

х>0;

^ 1-1, х<0.