Черненко В.Д. Высшая математика в примерах и задачах (том 3)

Подождите немного. Документ загружается.

60 Гпава 22

22.6.

Вычисление определенных

интегралов

Пусть требуется найти приближенное значение определен-

ного интеграла

[

f(x)dx

Для этого разобьем интервал интегри-

рования [ci,b] точками XpX2,...,x^_i на п равных частей

h = ,

JCQ

= а, x^=b я вычислим значения подынтегральной

функции в точках деления

Уо

= !(^)>

Ух

= !(^хh Уг = 1(^1

-..

Уп-х

и^п^х

Уп

= f(b)^

Представляя определенный интеграл в виде площади кри-

волинейной трапеции, используют одну из следующих прибли-

женных формул.

1°.

Формула прямоугольников

/=0

или

/г'

где

R^=:

—

(b-

u)f^'^

(t,) — предельная абсолютная погрешность

формулы прямоугольников; /^^ (^) - наибольшее значение про-

изводной в интервале

[а,

6].

Геометрическая площадь криволинейной трапеции аАВЬ

(рис.

22.6), которая соответствует определенному интегралу, за-

писывается суммой площадей заштрихованных прямоугольни-

ков.

Формула (1) соответствует схеме деления рис. 22.6, а и слу-

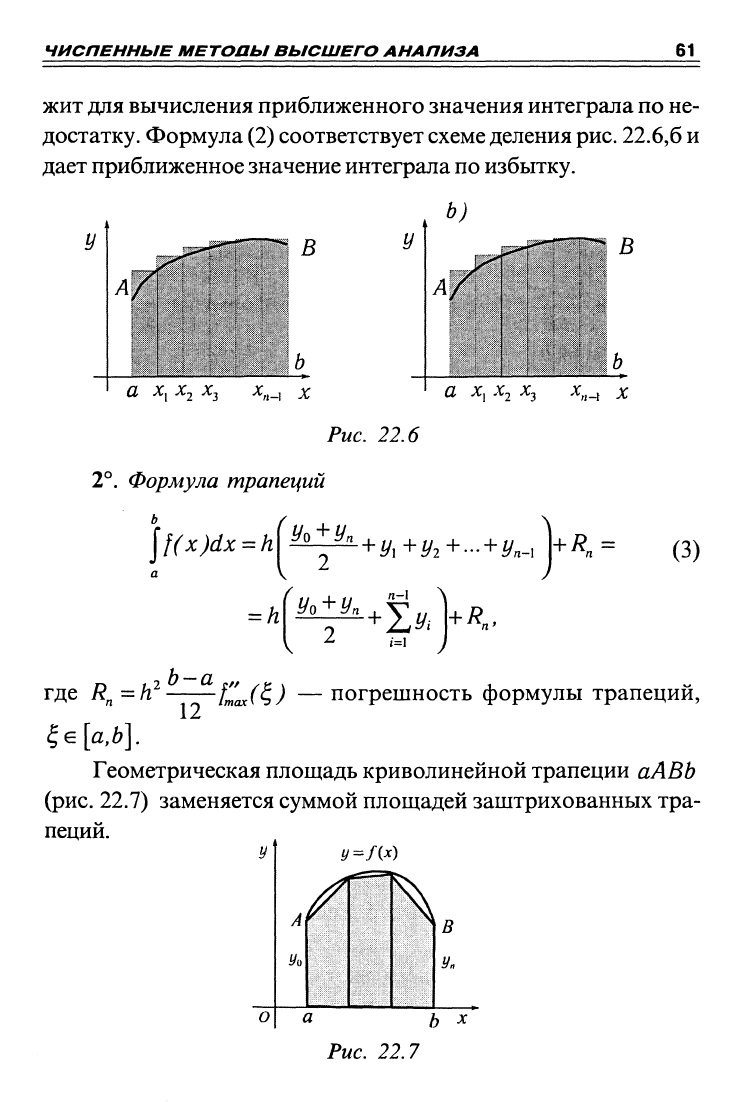
ЧИСПЕННЫЕ МЕТОаЫ ВЫСШЕГО АНАПИЗА

ЖИТ

для вычисления приближенного значения интеграла по не-

достатку. Формула (2) соответствует схеме деления

рис.

22.6,6 и

дает приближенное значение интеграла по избытку.

rj В

Г^.

CL Xj Xj Х^ X^,_j X

и Xj Х2 х^

x^^_j^

Рис. 22.6

2°.

Формула трапеций

\f(x)dx

= h

Уо+У.

+ У1+У2+-

+ У

п-\

\+к =

(3)

^^+1,У1

1=1

+к.

гЬ-а

где R„=h [тах(^) — погрешность формулы трапеций,

^е[а,Ь].

Геометрическая площадь криволинейной трапеции аАВЬ

(рис.

22.7) заменяется суммой площадей заштрихованных тра-

пеций.

Уо

)

У„

Рис. 22.7

62 Гпава 22

3°.

Формула

Симпсона

(параболических трапеций)

jf(x)dx

-[y,+y^+4(y,+y,+...

y„_,)+2(y^+y,+

Уп-2)]

^п=^(Ус+Уп+'^^.У2^-1+^1,У2к)

+ К'

k=l k=\

где R^

fma^^(^) —погрешность формулы;

—число

1 oO

четное;с^Е[а,6].

Геометрическая площадь каждой пары вертикальных кри-

волинейных трапеций является площадью параболической тра-

пеции (рис. 22.8), т. е. каждый участок кривой

у = f(x)

заменя-

ется дугой параболы

x^-{-px

проходящей через три точ-

ки кривой с абсциссами

х.,х.^^,х.^2

•

у ^х"

-{-

px+q

Рис.

22.8

Очевидно, что чем больше

п,

тем приближенное значение

определенного интеграла

точнее.

При одном и том же

форму-

ла трапеций точнее формулы прямоугольников, формула Симп-

сона точнее формулы трапеций. Если предельная абсолютная

погрешность задана

> О, то параметр

или число разбиений

п могут быть найдены из неравенства

|/?„ |

г .

При вычислении значений определенных интегралов на ЭВМ

погрешность целесообразно оценивать методом удвоения шага

вы-

ЧИСПЕННЫЕ МЕТОаЫ ВЫСШЕГО АНАПИЗА 63

числений. Полагая n

kii k =

вычисляем значение искомо-

го интеграла J^, k — четное. Затем удваивая число разбиений

2ки h2=

находим значение интеграла

J^.

Если l^ -^i

| <

то расчет заканчивается. Иначе снова удваиваем разбиение.

6,1.

Вычислить интеграл

i^JS

x^dx, разбивая интервал

интегрирования на 10 равных частей, по формулам:

а) прямоугольников; б) трапеций; в) Симпсона. Оценить по-

грешности результатов.

Решение, а) Делим интервал интегрирования [0,1] на 10

равных частей, находим точки деления х и значения подынтег-

ральной функции в этих точках у

= л]5 +

х^ :

г/о =75=2,2361,

г/, =^/5,001=2.2363,

г/2 =л/5,008 =2,2378,

г/з =75,027=2,2421

i/4 = 75.064 = 2,2503,

(/5=75,125=2,2638,

г/б =75,216 =2.2839,

^7=75,343=2,3115,

1/8=75,512=2,3478,

г/9 =75,729 =2,3935,

г/,о=7б

=2,4494.

X, :

Хб

Xg •

Хд •

-^10

= 0,

0,1,

= 0,2,

= 0,3,

= 0,4,

= 0,5,

= 0.6.

= 0,7.

= 0.8.

= 0,9,

64 Гпава 22

Длина одной

части

h = =

0,1.

По формуле

прямоуголь-

НИКОВ

(1) имеем /^

0,1^^^

2,2803

Для нахождения абсолютной погрешности формулы прямо-

угольников вычислим наибольшее значение производной в ин-

тервалеГОД] f(x)^ , /Vi; = 0,6124.

2V5

+ x'

Абсолютная ошибка приближенного значения по недостат-

ку равна R,

=—1,0716

= 0,0004.

По формуле прямоугольников (2) находим приближенное

значение по избытку /^ = 0,1Y

г/^

= 2,3016.

Абсолютная ошибка этого приближения равна /?„ = 0,0004.

б) По формуле трапеций (3) имеем

/ = 0,1

4,6855

^ "1

^ 1=1

2,291.

Абсолютная ошибка результата равна

Р= Mi

1,0716

0,0009

" 12

в) По формуле Симпсона получим

/ =

—(^2,2361

+ 2,4494+411,4472 + 2-9,1198; = 2,2905.

Для нахождения абсолютной погрешности вычисляем

/^,^ =1,6244. Абсолютная ошибка равна всего лишь

^ 00001 ^ 0000009.

" 180

ЧИСПЕННЫЕ МЕТОаЫ ВЫСШЕГО АНАПИЗА 65^

6.2. По формуле Симпсона вычислить приближенное значе-

\smxdx

ЛЛЛЛ1

ние интеграла с точностью до 0,0001.

{ х

+ 1

Решение. Сначала определим, на какое число частей п сле-

дует разбить интервал интегрирования

[О,

л:].

Поскольку требу-

ется точность

10"^,

то имеем

180п' """

Так

как/j^

=0,039; а = 0, Ь=к

Ъ,\А\59,

то окончатель-

4 л:'•0,039 10'' „^^,

но получим п > или п > 5,1.

Ближайшее четное число п

Находим точки деления х,.

sinx

ще им значение

Хо=0,

-у.

х^=к.

[

функции у =

х +

г/о=0.

г/, =0,3283

г/, =0,4235

f/з =0,3891

г/4

=0,2803

г/5

=0,1382

г/б=0-

Подставляя в формулу Симпсона

(4),

находим значение ин-

теграла с точностью 10"^

Г^^^^^ =

0.1744(^4

•

о,

8556 + 2 •

о,

7038;

= о,

84235.

66 Гпава 22

Современная вычислительная техника позволяет вычислять

интегралы

любой точностью, необходимой для практического

использования результатов расчета.

22Л.

Численное интегрирование

обыкновенных дифференциальных

уравнений

V. Метод

Эйлера.

Рассмотрим уравнение первого порядка

у'

- f(x, у). Требуется на отрезке

[XQ

х^

]

составить таблицу при-

ближенных значений частного интеграла, удовлетворяющего на-

чальному условию у^

у(х^).

Для этого разбиваем данный от-

резок точками ХрХ2,...,х^_1 на п частичных отрезков и находим

касательную

интегральной кривой на каждом участке.

Уравнение касательной на первом частичном отрезке

[XQ

х^

]

к искомой интегральной кривой в точке (х^,у^) имеет вид

у-Уо=У(Ч>Уо)(^-Ч)'

откуда при

находим приближенное значение искомого

интеграла у^ в точке х^

Ух

=Уо+(^1-^о)У(^о^Уо)' (1)

Аналогично, для отрезка

[х^,

^2 ]

в точке ^2 будем иметь

У2=Ух+(^2-^х)У(^Х>Ух) (2)

или для любого / -го отрезка

М-

Уы

+ (^i -

^i-x

)y(h-x'

У1-х) = У1-х

+ hy(x._,, //._,; (3)

где в случае частичных отрезков одинаковой длины длина од-

—

ного отрезка h = -^

Таким образом, процесс интегрирова-

ния сводится к замене интегральной кривой ломаной, состоящей

из отрезков касательных.

ЧИСПЕННЫЕ МЕТОПЫ ВЫСШЕГО АНАПИЗА

67^

При увеличении

длина частичных отрезков уменьшается

и точность решения возрастает.

2°.

Метод Рунге-Кутта, Пусть требуется на отрезке

[х^,

х„

]

найти

заданной степенью точности

решение уравнения

у'

f(x,y),

удовлетворяющее начальному условию

у^ =

у(х^).

Сначала делим отрезок

[^о^^п] ^^ ^

равных частей

—

= -^ так,

чтобы

h"^

<£

Тогда метод Рунге-Кутта имеет

погрешность h

"*.

Точки деления

х. (i

0,\,...,n)

находим по фор-

муле

=XQ+ ih

Соответствующие значения искомой функции

у.

= у(х.)

ПО

методу Рунге-Кутта находятся

по

формуле

где

А^. = -(а. +

26.

2с.

d.);

a,=hf(x,,y,);

zy h b. .

hf(x,-^-,

у-Л-^);

d.=h[(x.

y^+c-).

Точность метода Рунге-Кутта приближенно может быть

определена

из

принципа Рунге

—1//2^-^^|,

где

У2т>Ут

—

результаты вычислений

шагом

h и 2/г, п

2т .

Метод Рунге-Кутта легко обобщается

и на

решение систе-

мы

дифференциальных уравнений

у'

= [(х,

у,

t); X =

(р(х,

уЛ), (5)

удовлетворяющий начальным

условиям:

—

х^,

У — Уо

при t^t^.

пава

3°.

Метод Милна. Требуется найти на отрезке

[^с-^л]

Р^"

шение уравнения if =

f(x,y),

удовлетворяющее начальному ус-

ловию у^

y(xQ). Для этого находим каким-либо способом три

последовательные значения

Ух=У(^х)> У2=У(^2)> Уз=У(^з)

искомой функции (например, методом Эйлера или Рунге-Кутта)

и т. д.

Последующие значения у. (i

4,5,.,.,n)

вычисляем по фор-

мулам

4/г

У1

= У1-4+yf'^ts - L2+L

Л*

(6)

"^^^

fi=f(Xi>yi) = yl' Ji=ff(^i^yi)'

Контроль расчета определяется величиной £.

—

- ^ .

Если £.

10""",

где т — последний десятичный разряд, сохра-

няемого в ответе знака, то за

у^

принимаем ^. и вычисляем сле-

дующее значение функции //.^,. Если же

£^

Ю"'", то следует,

уменьшив шаг разбиения, расчет провести сначала. Для опреде-

ления величины начального шага можно воспользоваться нера-

венством /г^ <10""'.

Метод Милна может быть использован и для решения сис-

темы уравнений (5). В этом случае формулы Милна пишутся

отдельно для функций x(t) и

[/("^^.

Дальнейший порядок вычис-

лений остается без изменений.

4°.

Метод Адамса. Требуется найти на отрезке

[А:О,Х„]

ре-

шение уравнения у'

f(x, у), удовлетворяющее начальному ус-

ЧИСПЕННЫЕ МЕТОДЫ ВЫСШЕГО АНАПИЗА

ЛОВИЮ у^

у(х^).

Найдем сначала каким-либо способом (ме-

тодом Эйлера или Рунге-Кутта и т. д.) три последовательные

значения искомой функции

yi=y(^il У2=У(^21 Уз=У(^)'

Введем обозначения

Яо

%о

hf(x^,yj,

q, = hy\ =

hf(x,,yj;

Ri = hy[ = hf(x^,

y^;,

hy^

= hf(x^,

y^)

(7)

и составим диагональную таблицу конечных разностей ве-

личины q (вычисленные величины расположены выше пунк-

тирной линии).

\ч

Хз

\х.

Уо

Ух

Уг

Уз

УА

Уь

Уб

АУ =

Уп^^-Уп

Аг/о

Аг/,

^Уг

^Ул

Аг/5

У =

f(x.y)

!(Хо,Уо)

f(Xi,yJ

К^г.Уг)

!(^'Уъ)

fi^A'yJ

f(x„ys)

= y'h

Яо

<?i

Ъ .

ЯА

Aq =

А<7о

А^,

А^2 ,

.-'А^7з

А?4

^\.'

.-г\

А%

А'^о.-'

''А^'7.

А\

Продолжение диагональной таблицы разностей вычисляет-

ся по формуле Адамса

15 3

(8)