Черненко В.Д. Высшая математика в примерах и задачах (том 3)

Подождите немного. Документ загружается.

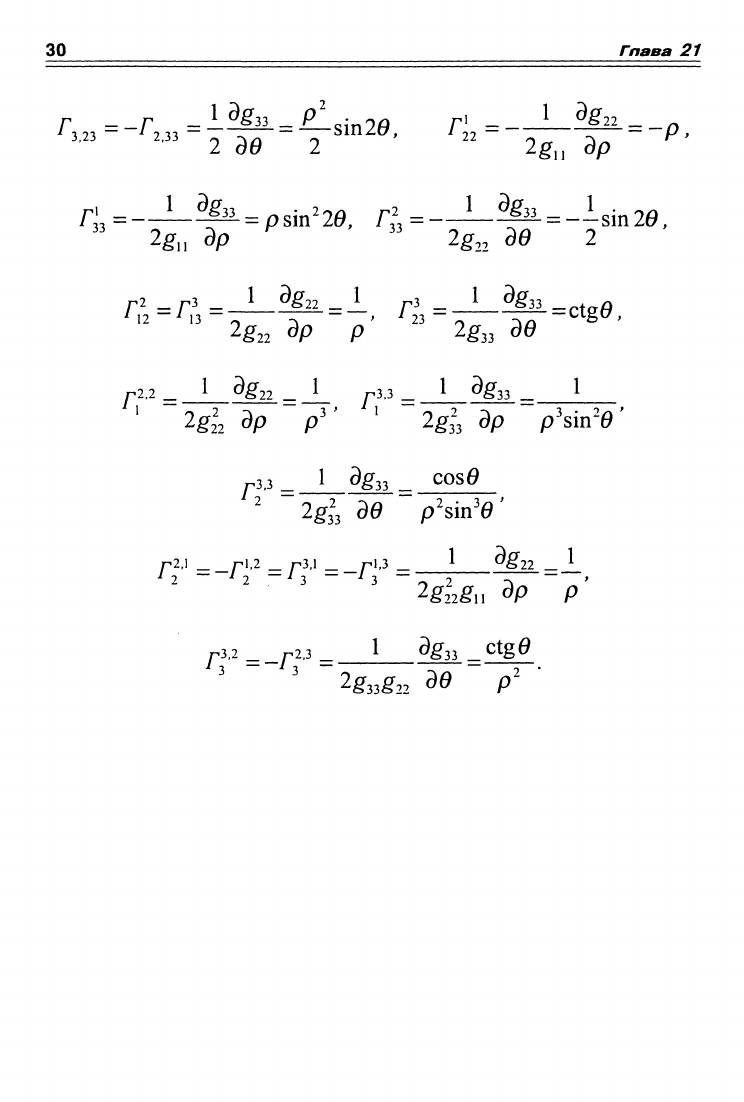
30 Гпава 21

3,23

2,33 2 Э0 2 '' 2g„ dp ^

2g„ Эр ^ " 2g,, de 2

Чгг Эр P '' 2^33 de

^2,2 ^ ^ ^g;2 ^

_1_

3.3

^ 1 3g33 1

2|Г22 Эр p' 2^3-3 Эр phm-e

3,3 _ 1^Э§з^_^О80^

2^33 Э0 p^sin^e'

1г -1г -^ -/з

-2^2^^^_

Зр -р'

Г"

=-Г" 1 9g33^ctg0

' 2^33^22 Эв р'

Глава 22

ЧИСЛЕННЫЕ МЕТОДЫ ВЫСШЕГО

АНАЛИЗА

22.1.

Действия с приближенными числами

1°.

Абсолютная

погрешность.

Пусть а есть приближенное

значение числа А, т. е. А- а. Абсолютной погрешностью при-

ближенного числа а, заменяющего точное значение числа А,

называется абсолютная величина разности между ними

\А-а\<А,

где Д — предельная абсолютная погрешность, т. е. наименьшая

из верхних граней абсолютной погрешности. Точное число А на-

ходится в пределах А

а±А или

а-А<Л<а

А.

На практике

предельная абсолютная погрешность может быть представлена,

например, лЯ =

14141

0,0001.

2°.

Относительной погрешностью S приближенного числа

а называется отношение абсолютной погрешности числа

к точ-

ному числу А

32 Гпава 22

где 5 — предельная относительная погрешность. На практике

предельную относительную погрешность иногда вычисляют по

формуле 5=—, так для A

yj2 и а =

1,4142

= —

= 0,00007. Относительная погрешность выражается

отвлеченным числом. Если приближенное число а принять за

100%,

то относительная погрешность 5 будет выражаться в

процентах.

3°.

Округление приближенного числа заключается в замене

его числом

меньшим количеством значащих цифр:

а) если отбрасываемые цифры начинаются с цифры мень-

шей 5, то остающиеся цифры не меняют;

б)

если отбрасываемые цифры начинаются

цифры большей

то последнюю из оставшихся цифр увеличивают на единицу;

в) если первая отбрасываемая цифра равна

и среди следу-

ющих за ней цифр есть отличные от нуля, то последнюю из ос-

тавшихся цифр увеличивают на единицу;

г) если первая отбрасываемая цифра равна 5, а все следую-'

щие нули, то последняя из оставшихся цифр увеличивается на

единицу, когда та нечетная, и остается без изменения, когда чет-

ная.

4°.

Запись приближенных чисел и верные цифры. Правило

записи приближенных чисел

любой системе счисления состоит

в том, что последняя значащая цифра должна быть верной. Ог-

раничимся десятичной системой счисления. Значащей цифрой

приближенного значения числа называется всякая отличная от

нуля цифра его десятичной записи и нуль, если он приходится

между значащими цифрами или является представителем сохра-

ненного десятичного разряда. Так, приближенное значение

0,03040

содержит четыре значащие цифры. Приближенное чис-

ло а >

имеет п верных десятичных знаков в узком смысле.

ЧИСПЕННЫЕ МЕТОаЫ ВЫСШЕГО АНАПИЗА 33

если абсолютная погрешность этого числа не превышает

—

еди-

ницы п

-го

разряда значащей

цифры.

Например, для числа 212,64

число 213,00 является приближенным значением

тремя верны-

ми цифрами, так как |212,64-213,00| = 0,34<—10°. Запредель-

ную относительную погрешность в этом случае можно принять

число о = —

. . 1 Г 1 Y

первая значащая цифра числа а.

В частности, если 5 <

—

, то число заведомо имеет п вер-

ных знаков в узком

смысле.

Если абсолютная погрешность при-

ближенного числа не превышает единицы последнего порядка,

то все десятичные знаки п этого приближенного числа а явля-

ются верными в широком смысле ^ =

—

процессе промежуточньгс вычислений приближенные

чис-

ла могут содержать одну-две запасные цифры. При наличии в

приближенном числе большего количества значащих цифр окон-

чательный результат, как правило, округляется до числа цифр

верных в узком или широком смысле.

5°.

Арифметические действия с приближенными числами.

Предельная абсолютная погрешность алгебраической суммы рав-

на сумме предельных абсолютных погрешностей складываемых

чисел. Если суммируются приближенные числа с разными чис-

лами верных знаков, то следует подравнять все слагаемые по

образцу числа, десятичная запись которого обрывается ранее

других, сохраняя в каждом из других слагаемых запасной знак.

Полученные числа складываются как точные и сумму округля-

ют на один

знак.

Если складываются неокругленные приближен-

ные числа, то лишние знаки удерживаются до конца вычисле-

ний. Относительная погрешность суммы положительных чисел

34 Гпава 22

не превышает наибольшей из относительных погрешностей сла-

гаемых.

случае разности двух близких приближенных чисел отно-

сительная погрешность может не содержать достоверных зна-

ков.

Поэтому следует избегать этой нежелательной операции.

Относительная погрешность произведения и частного при-

ближенных чисел равна сумме предельных относительных по-

грешностей этих

чисел.

Отсюда, как следствие — предельная от-

носительная погрешность k -й степени приближенного числа а

равна k -кратной предельной относительной погрешности этого

числа, а предельная относительная погрешность корня k -й сте-

пени составляет

—

-ю часть предельной относительной погреш-

ности приближенного числа а,

6°.

Пусть Afl^,..., Аа^ — предельные абсолютные погрешно-

сти приближенных чисел

ар...,

а^. Тогда абсолютная погреш-

ность результата различных действий S

S(a^,a^,...,a^) над

приближенными числами приближенно оцениваются формулой

AS =

Э5

дсц

Aai+...+

Э5

Эа.

Аа.

Предельная относительная погрешность, соответственно,

равна

\S\

Если суммарные погрешности AS и 8S заданы, то полагая

все частные производные в предыдущих формулах равными,

можно найти необходимые для вычислений допустимые абсолют-

ные погрешности приближенных чисел.

1.1. Вычислить абсолютные и относительные погрешнос-

ти приближенных чисел, верных в узком и широком смысле в

написанных знаках: а)

427,3;

б) 0,072; в) 37,81 кг;

ЧИСПЕННЫЕ МЕТОаЫ ВЫСШЕГО АНАПИЗА 35^

г) 25°0Г53"; д) 15,1 см.

Решение, а) Абсолютная погрешность приближенного чис-

ла, имеющего п верных знаков в узком смысле, не превышает

половины единицы разряда, выраженного п -й значащей циф-

рой

десятичной записи. Следовательно,

= 0,05. Относитель-

ная погрешность в этом случае

а 427,3

Абсолютная погрешность приближенного числа, имеюще-

го п верных знаков в широком смысле, не превышает единицы

разряда, выраженного п -й значащей цифрой. Следовательно,

д =

0,1.

Относительная погрешность

а М1,Ъ

б)

Абсолютная

относительная погрешности чисел, верных

в узком смысле

0,0005,

^^55^i55^

0,694%.

0,072

Для чисел, верных в широком смысле в написанных знаках

д =

0,001;

^^0.00М00%^,ззо^,

0,072

в) Для чисел, верных в узком смысле:

0,005

кг; д= = 0,0132%.

37,81

В широком смысле:

л ПЛ1 9i о>оыоо%

^^^.о/

Д = 0,01/сг; д= = 0,026%.

37,81

г) Для чисел, верных в узком смысле:

д=0,5";

5=^^^-^^=0,00055%

90113

36 Гпава 22

Вшироком: А = Г; 8 =

^'^^^^=0.0011%.

90113

д) Для чисел, верных в узком смысле

л лп^ ^ 0,05100% ^„.0/

= 0,05

еж;

о- =

0,331%.

широком: А =

0,1

см; S = ^^^'^^^^ = 0,662%.

1.2. Определить число верных в узком смысле знаков и дать

соответствующую запись приближенных чисел: а) 425627 при

точности в 1%; б) 11,2930 при точности 2%.

Решение, а) Принимая приближенное число за

100%

и учи-

тывая, что относительная погрешность составляет

1%,

находим

абсолютную погрешность

4256.

Приближенное

число

430000

имеет два верных знака в узком смысле, поскольку абсолютная

погрешность

не

превышает -- единицы четвертого разряда зна-

чащей цифры |425627 -

430000|

= 4673 < 0,5

•

10^

Окончательно получим 430000 ±

4000.

б) Поскольку относительная погрешность составляет

2%,

то

принимая приближенное число за 100%, находим абсолютную

погрешность

= 0,22586. Приближенное число 11,3000 имеет

три верных знака, так как |l

1,2930-11,3000|

= 0,007<0,5-10'\

Таким образом,

11,3

+ 0,2.

1.3. Выполнить арифметические действия

приближенными

числами, верными в написанных знаках: а) 172,36+23,7+0,413;

б) 161,4-43,217; в) 6,3-1,147; г) 0,421:1,6; д) 32,4^; е) ТтДб .

Решение, а) Поскольку десятичная запись среднего сла-

гаемого заканчивается ранее других, то подравняем два дру-

гих по образцу среднего слагаемого, сохраняя в каждом из

них запасной знак, и сложим полученные числа, округляя сум-

ЧИСПЕННЫЕ МЕТОаЫ ВЫСШЕГО АНАПИЗА 37

му на

ОДИН

знак 172,3(6) + 23,7 +

0,4(1)

= 196,5.

б) Аналогично 161,4-43,2 (1) = 118,2.

в) Поскольку предельная относительная погрешность про-

изведения приближенных чисел равна сумме предельных отно-

сительных погрешностей этих чисел, то, предполагая, что все

знаки сомножителей верные, получим

=-^0,1

+ — 0,001-0,0088.

2-6 21

Отсюда следует, что число верных знаков равно трем и ре-

зультат примет вид

6,3-1,147

= 7,23 или

6,3-1,147

= 7,22±0,06.

г) Находим предельную относительную погрешность

5= —-0,001 + — 0,1-0,050125.

2-4 21

Так как число верных знаков равно одному, то результат

примет вид

0,421:1,6

= 0,26 или

0,421:1,6

= 0,3

±0,1.

д) Находим предельную относительную погрешность

5=1.0,1 = 0,03.

Число верных знаков квадрата 32,4^ = 1049,76 равно трем,

а абсолютная погрешность

31.

Тогда значение числа нахо-

дится в пределах

1040

±31.

е) Относительная погрешность приближенного числа

V7,16 =

—

•—10"^

=0,0007; абсолютная погрешность равна

2,676

0,0007

= 0,002. Таким образом, ^ТДб =

2,676±

0,002.

1.4. Вычислить 1п(а

^[Ь), если а = 15,7; Ь = 21,4 — при-

ближенные числа, верные в написанных знаках.

Решение. Найдем сначала предельную абсолютную погреш-

ность AS в общем виде. Обозначим S

ln(a

\/b), тогда

38 Гпава 22

AS =

1 1 А6

Аа + —r=

24b

. Абсолютная погрешность чисел:

a-\-4b\

Аа

0,05;

АЬ

0,05.

Относительная погрешность приближенно-

1 1

го числа ^/21~4 = 4,6 равна S- 10 '

погрешность будет

= 4,63

•

0,025

= 0,1 •

Следовательно,

0,025;

абсолютная

AS:

15.7

+ 4,6

V05+' "-"^^

0,05

20,3

2 4,6

Учитывая, что сотые доли верны, получим

(l5,7+ 7214)== 3,01.

+ 0,11) = 0,003.

26*2*

Методы решения алгебраических

и трансцендентных уравнений

1°.

Кубическое уравнение:

х^

ах^ +Ьх

+ с =

(1)

Кубическое уравнение с помощью подстановки x

z —

приводится к уравнению вида г^ + рг + ^ =

О,

которое по форму-

ле Кардано имеет решение

Ll+A^^^+J-l-A^^^=u

(2)

гдеА = -+-.

Если А >

О,

то Zi=Ui

D,;

ы, +и,

±гл/з

^1-^1

ЧИСПЕННЫЕ МЕТОПЫ ВЫСШЕГО АНАПИЗА 39

где

W,,

и,

— вещественные значения корней « и

Если А =

О,

то 2, = —, Z, = 2, = —2..

р 2

Если 2<0,то z,=2J-—cos—,

3=2.1-—cos

~ 3

где cos(p

--^\——.

1 Ш

2°.

Отделение вещественного корня

уравнения.

Пусть дано

уравнение f(x)

= 0.

Между аи b содержится единственный ко-

рень уравнения ^ е

(а,Ь),

сеян [(а)и f(b) имеют разные знаки,

т. е. f(a)'[(b)<0, и функция f(x) в промежутке [ci,b] непре-

рывна вместе со своими производными f(x) и

f''(x),

причем

обе производные на всем промежутке сохраняют знак. Отрезок

[а,

6] н?iзывгieтcя

отрезком изоляции корня.

Действительные корни уравнения [(х) =

можно найти и

графически, поскольку корни являются абсциссами точек пере-

сечения кривой у

f(x)

осью Ох. Иногда бывает удобнее урав-

нение f(x) -

представить в виде ср(х)

\ff(x).

Тогда действи-

тельными корнями будут абсциссы точек пересечения кривых

(р(х) и у

\1/(х).

3°.

Метод хорд. Требуется определить действительный ко-

рень уравнения f(x)

= 0.

Рассмотрим график функции у

f(x)

(рис.

22.1) на отрезке

[а,

6].

Пусть f(a) <

и f(b)

на — тот из концов отрезка изо-

ляции корня, на котором f(a)

•

f(b)

О.

Соединим точки А и В

хордой. Тогда приближенным значением корня ^ будет точка

Xj пересечения хорды АВ с осью Ох

(b-a)f(a)

f(b)-f(a)'

(3^

X, =а~-