Чейз, Ричард, Б., Эквилайн, Николас, Дж., Якобе, Роберт, Ф. Производственный и операционный менеджмент
Подождите немного. Документ загружается.

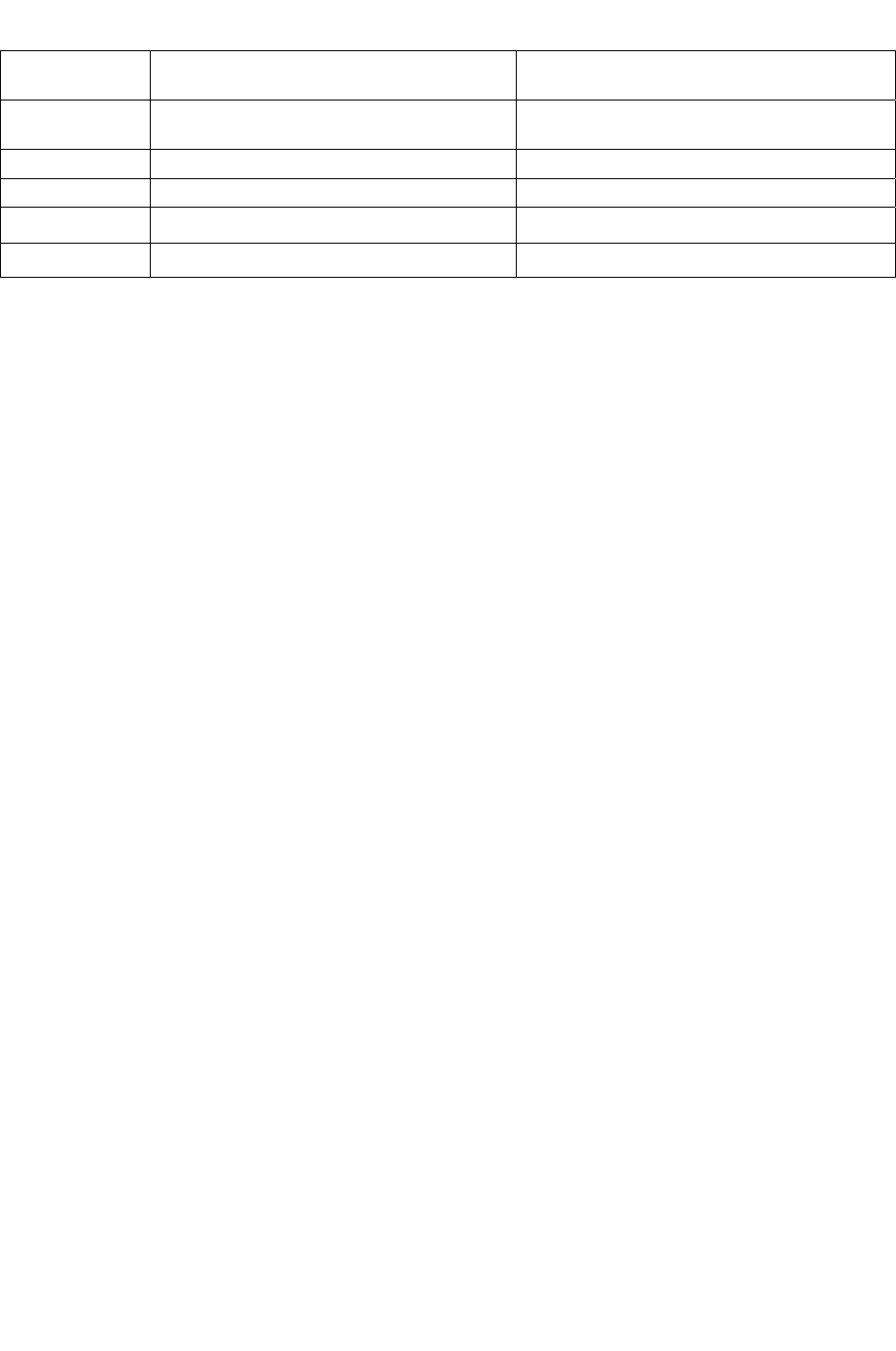
561
Таблица 13.5. Процент точек, попадающих в контрольные границы для MAD в диапазоне от 1 до 4
Контрольные
границы
Отклонение
MAD
Относительное число стандартных
отклонений
Процент точек, лежащих в
контрольных границах
+1 0,798 57,048
+2 1,596 88,946
+3 2,394 98,334
±4 3,192 99,856
Линейный регрессионный анализ
Регрессию можно определить как функциональную зависимость между двумя или
несколькими коррелированными переменными. Ее используют для предсказания значения
одной переменной на основе значения другой. Взаимосвязь обычно устанавливают на
основе наблюдаемых данных. Вначале по этим данным полезно построить график, чтобы
посмотреть, является ли зависимость линейной или частично линейной.
График линейной регрессии выражается уравнением Y = a + bХ, где Y— значение
зависимой переменной, относительно которой решается уравнение; a — отрезок,
отсекаемый на координатной оси Y; b — угол наклона прямой; X — независимая
переменная (в анализе временных рядов X обозначает текущее время).
Линейная регрессия эффективна при долгосрочном прогнозировании и совокупном
планировании. Например, линейная регрессия незаменима при прогнозировании спроса на
семейства изделий. Часто спрос на отдельные изделия в пределах семейства может
довольно широко варьировать во времени, хотя общий спрос на семейство изделий на
удивление сглаженный.
Главным ограничением прогнозирования с использованием линейной регрессии
является то, что, как подразумевает само название метода, заранее допускают, что
значения данных на прошлых и будущих интервалах попадают на прямую линию. Такое
допущение в целом ограничивает применение метода, поэтому к линейному
регрессионному анализу часто прибегают при исследованиях на небольших интервалах
времени. Однако продолжительный период можно представить в виде суммы коротких
отрезков времени; в которых наблюдается относительная линейность, что позволяет
обойти это ограничение.
Линейную регрессию используют для прогнозирования как в моделях временных
рядов, так и в причинных моделях. Когда зависимая переменная (на графике обычно
откладывается по вертикальной оси) изменяется в зависимости от времени
(откладываемого на графике по горизонтальной оси), имеют дело с анализом временных
рядов. Если одна переменная изменяется при изменении другой переменной, это
называется причинной связью (например, число умерших от рака легких зависит от числа
курящих).
На примере 13.2 сравним модели прогнозирования и виды анализа. Мы покажем
построение графика вручную, метод наименьших квадратов и декомпозицию.
Пример 13.2. Ручная аппроксимация трендовой линии
Данные о продажах изделий фирмы в течение 12 кварталов за последних 3 года
приведены в таблице.

562
Квартал Продажи Квартал Продажи
1 600
7
2600
2 1550 8 2900
3 1500 9 3800
4 1500 10 4500
5 2400 11 4000
6 3100 12 4900
Фирма хочет получить прогноз на каждый квартал четвертого года, т.е. на 13-,14-,
15- и 16-й кварталы. При ручной аппроксимации кривой на координатную сетку наносят
данные и либо оценивают их визуально, либо методом визуальной эвристической
аппроксимации (Ocular Heuristic Approximation — ОНА).
Решение
Процедура довольно проста: положите линейку (подойдет обычная пластмассовая
линейка) на точки нанесенных данных, таким образом, чтобы на прямую попало как
можно больше точек, и проведите линию. Это и есть линия регрессии. Следующим шагом
является определение отрезка а, отсекаемого на координатной оси У, и о — коэффициента
наклона прямой.
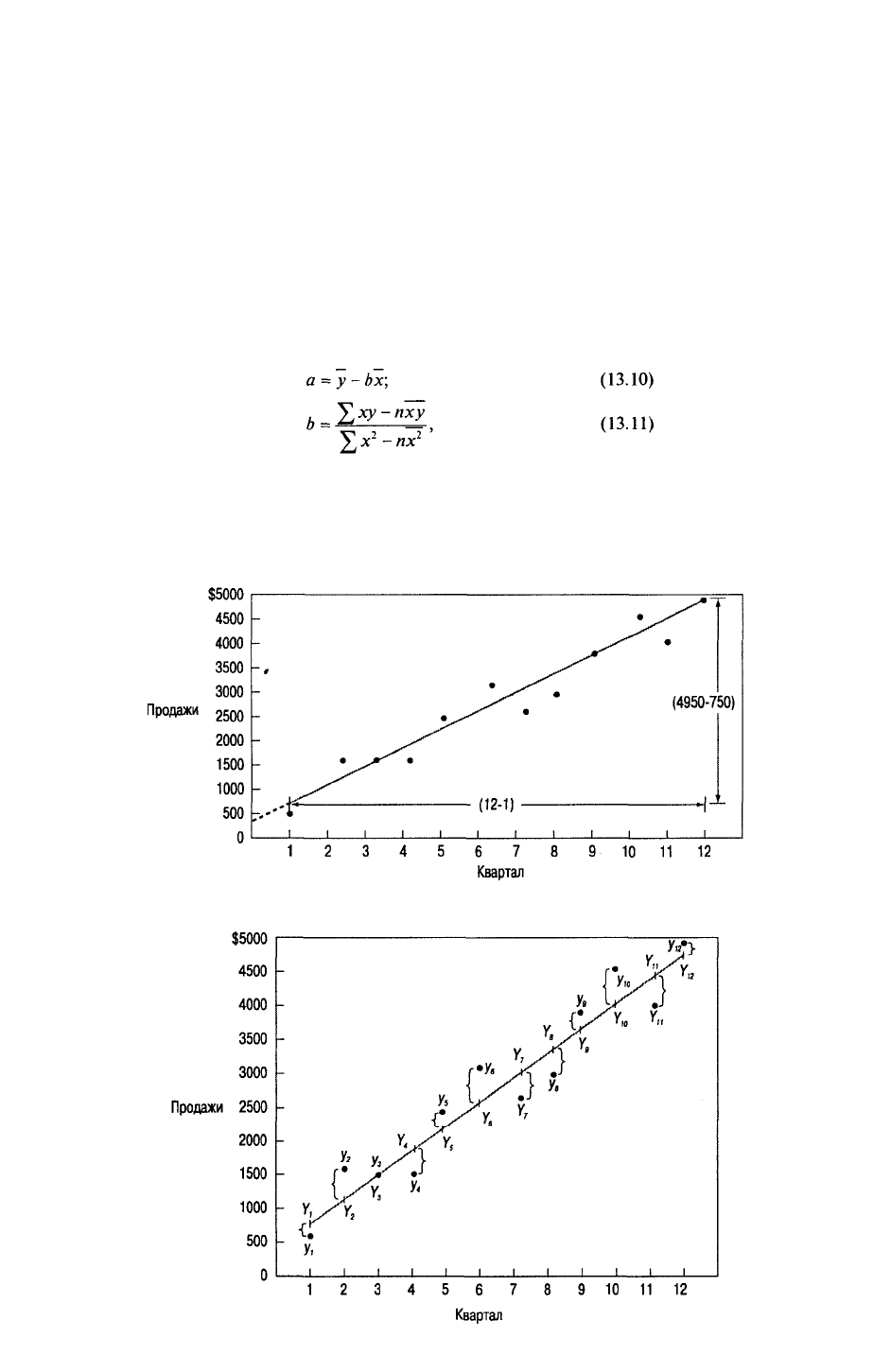
На рис. 13.7 показан график с нанесенными на него данными и вычерченная прямая,
проходящая через эти точки. Длина отрезка, отсекаемого на координатной оси У, равно
приблизительно 400. Коэффициент наклона прямой — это проекция некоторого отрезка
прямой линии на ось У, деленная на его проекцию на горизонтальную ось. Можно
использовать любые две точки, но две точки, взятые на большем расстоянии, дают более
высокую точность. В данном примере использовали значения 1-го и 12-го кварталов.
По графику на рис. 13.7 находим, что значение продаж для 1-го квартала равняется
примерно 750, а для 12-го — 4950. Поэтому: b = (4950 - 750)/(12 - 1) = 382.
Тогда уравнение регрессии, получаемое методом ручной аппроксимации, будет:
Y=400 + 382х.
Прогнозы на кварталы 13-16 будут следующими:
Квартал Прогноз
13 400 + 382x13=5366
14 400 +382 х 14 = 5748
15 400 + 382x15 = 6130
16 400 + 382x16 = 6512
Эти прогнозы, полученные графическим способом, не учитывают сезонные или
циклические колебания.
Метод наименьших квадратов. Уравнение наименьших квадратов для линейной
регрессии аналогично использованному в примере ручной аппроксимации и имеет такой
вид:
Y=a + bx, (13.9)
где Y — зависимая переменная, вычисляемая с помощью
данного уравнения;
у — текущее значение зависимой переменной;
а — отрезок, отсекаемый на координатной оси У;
b — коэффициент наклона прямой;
х — период времени.
563
С помощью метода наименьших квадратов можно построить линию регрессии по
значениям данных таким образом, чтобы минимизировать сумму квадратов
вертикального расстояния между значением каждой точки данных и значением
соответствующей ей точки на линии регрессии. На рис. 13.7 показаны 12 точек. Если
прямая линия проведена через общую область точек, то разность значений (отклонение)
между точкой и линией, измеренная по вертикали, будет равна у — Y. На рис. 13.8
показаны эти разности (отклонения).
Сумма квадратов отклонений фактических значений, нанесенных на график, от
соответствующих значений линии регрессии будет равна:
(y
1
-y
1
)
2
+ (y
2
-y
2)
2
+... + (У
12
-У
12
)
г
.
Наилучшей линией регрессии будет линия, которая минимизирует эту сумму.
Как и раньше, уравнение прямой линии имеет такой вид: Y = а + bх.
Для этого уравнения нужно определить а и b. При методе наименьших квадратов
формулы для определения а и b будут следующими:
где а — отрезок, отсекаемый на координатной оси Y; b — величина наклона прямой;
у — среднее всех значений у;
х — среднее значение всех х;
х — значение х для каждой точки данных (текущее значение);
Рис. 13.7. Линия регрессии, построенная ручной аппроксимацией
Рис. 13.8. Линия регрессии, построенная методом наименьших квадратов

564
у — значение у для каждой точки данных (текущее значение);
п — число точек данных;
Y — значение зависимой переменной, вычисляемое по уравнению регрессии.
В табл. 13.6 для примера 13.2 приведены вычисления для 12 точек данных,
показанных на рис. 13.7. Следует отметить, что окончательное уравнение для Y дает
длину отсекаемого отрезка, равную 441,6, и коэффициент наклона прямой — 359,6.
Наклон показывает, что изменение X на единицу приводит к изменению Y на 359,6
единиц.
Теперь по уравнению регрессии рассчитаем прогнозы для периодов 13—16, которые
будут следующими: Y
13
=441,6 + 359,6x13 = 5116,4;
Y
14
=441,6 + 359,6x14 = 5476,0; Y
15
=441,6 + 359,6x15 = 5835,6; Y
16
=441,6 + 359,6x16
= 6195,2. Стандартную ошибку оценки (аппроксимации) определяют по формуле
4
:
4
Формула упрощенного вычисления стандартной ошибки имеет такой вид:
В нашем примере стандартную ошибку прогноза вычислим по данным второй и
последней колонок табл. 13.6:
Возможное существование сезонных компонентов будет обсуждаться при
разложении временных рядов в следующем разделе.
Разложение (декомпозиция) временных рядов
Временные ряды можно определить как данные, расположенные в хронологическом
порядке, которые могут содержать один или несколько компонентов спроса: трендо-вый,
сезонный, циклический, автокорреляционный и случайный. Разложение (декомпозиция)
временного ряда означает идентификацию и разделение данных временного ряда на эти
компоненты. На практике относительно несложно идентифицировать тренд (даже без
математического анализа можно построить график и определить направление движения) и
сезонный компонент (путем сравнения с аналогичным периодом другого года).
Значительно сложнее идентифицировать циклы (выраженные количеством месяцев или
лет), автокорреляцию и случайные компоненты. Составители прогнозов обычно называют
случайностью все, что вне границ их понимания, и все, что не поддается идентификации
подобно другим компонентам.
Таблица 13.6. Метод наименьших квадратов: расчетные данные
X y ху x
2
y
2
Y
1 600 600 1 360 000 801,3
2 1550 3100 4 2 402 500 1160,9
3 1500 4500 9 2 250 000 1520,5
4 1500 6000 16 2 250 000 1880,1
5 2400 12 000 25 5 760 000 2239,7
6 3100 18 600 36 9 610 000 2599,4
7 2600 18 200 49 6 760 000 2959,0
565
8 2900 23 200 64 8 410 000 3318,6
9 3800 34 200 81 14 440 000 3678,2
10 4500 45 000 100 20 250 000 4037,8
11 4000 44 000 121 16 000 000 4397,4
12 4900 58 800 144 24 010 000 4757,1
78 33 350 268 200 650 112 502 500
х = 6,5; b = 359,6153;
у = 2779,17; а = 441,6666;
Y = 441,66 + 359,6х;
5
yx
=363,9.
Когда в спросе одновременно действуют сезонные и трендовые компоненты,
возникает вопрос их влияния друг на друга. В этом разделе будет рассмотрено два типа
сезонных колебаний: аддитивный и мультипликативный.
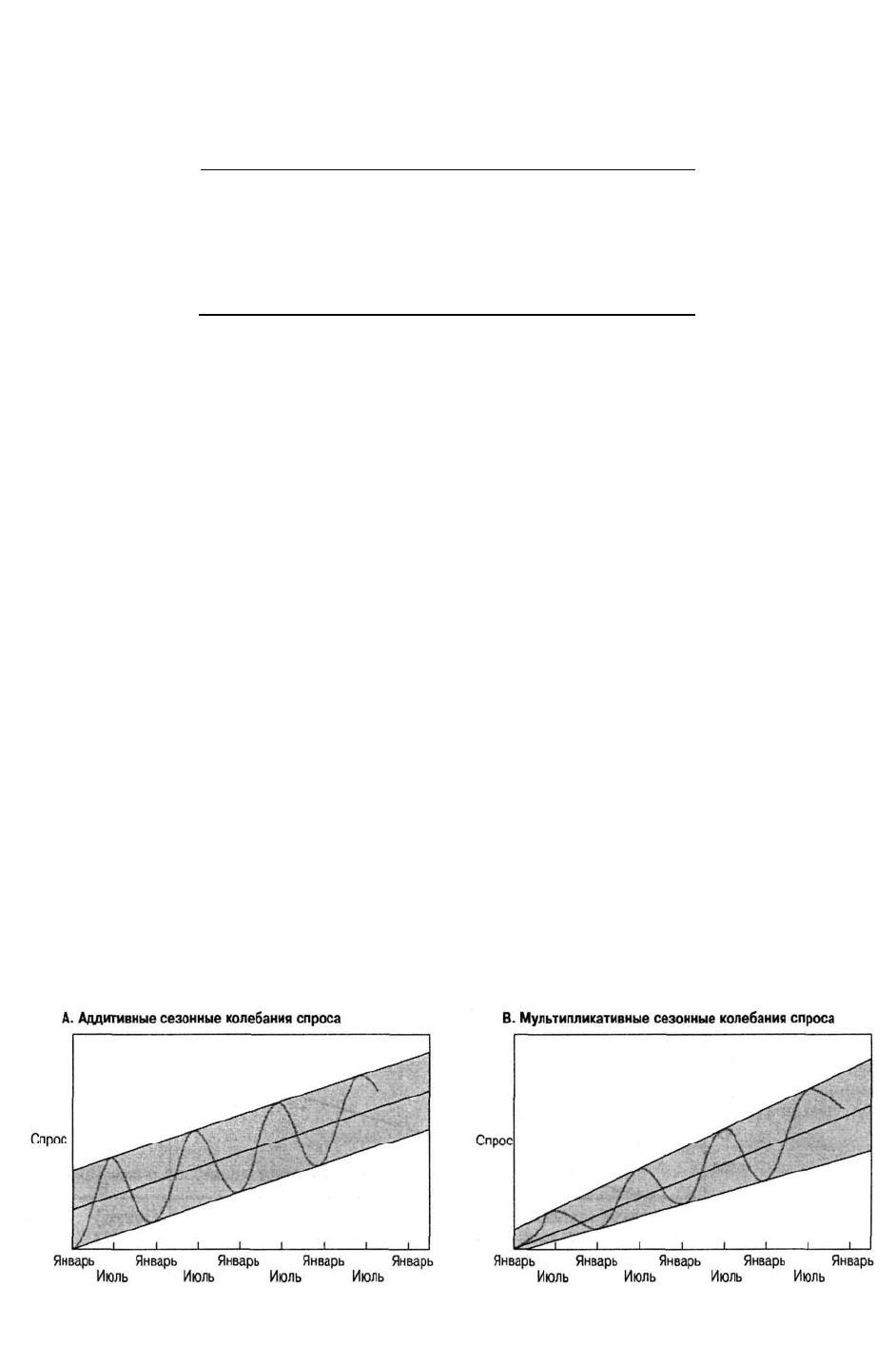
Аддитивные сезонные колебания. К аддитивным сезонным колебаниям относят те
колебания спроса, которые не зависят от тренда и среднего спроса.
Прогноз, включающий тренд и аддитивный сезонный компонент, равен тренду,
плюс сезонный компонент.
На рис. 13.9 (часть А) показан пример возрастающего тренда с аддитивными
сезонными колебаниями спроса.
Мультипликативные сезонные колебания В случае мультипликативных сезонных
колебаний при определении прогноза значения тренда умножают на значения сезонного
компонента.
Прогноз, включающий тренд и мультипликативный сезонный компонент, равен
тренду, умноженному на сезонный компонент.
На рис. 13.9 (часть В) показано увеличение сезонных колебаний по мере роста
тренда, в случае существования зависимости сезонных колебаний от тренда.
Мультипликативные сезонные колебания лучше, чем аддитивные, описывают
реальные процессы, так как из практики хорошо известно, что, чем больше продажи, тем
большими будут их колебания.
Сезонный индекс — это корректирующий коэффициент, который необходимо
ввести во временной ряд для учета колебаний спроса по сезонам года.
Обычно термин сезонный ассоциируется со временем года, в то время как термин
циклический используют для определения не годовых, а любых других повторяющихся
процессов.
Рис. 13.9. Совместное с трендом действие аддитивных и мультипликативных сезонных колебаний
566
Примеры ниже показывают, как определяют и используют сезонные индексы для
прогнозирования с помощью:
• простого расчета, основанного на данных прошлого сезона;
• использования тренда.
Мы выполним эти расчеты, следуя довольно формальной процедуре разложения
данных и прогнозирования с помощью регрессионного анализа методом наименьших
квадратов.
Пример 13.3. Простая пропорция
Примем, что за прошедшие годы фирма продавала товар в среднем по 1000 единиц
ежегодно. В среднем 200 единиц продавалось весной, 350 — летом, 300— осенью и 150—
зимой. Сезонный индекс — это отношение количества товара, проданного в каждом
сезоне, к среднему за год сезонному количеству.
Решение
В этом примере, если разделить годовое значение продаж на число сезонов, то
среднее за год сезонное количество будет равно: 1000/4 = 250. Поэтому сезонные индексы
будут следующими.
Прошлые
продажи
Средний уровень продаж за каждый
сезон (1000/4)
Сезонный индекс
Весна 200 250 200/250 = 0,8
Лето 350 250 350/250 = 1,4
Осень 300 250 300/250 = 1,2
Зима 150 250 150/250 = 0,6
Сумма 1000 1000
Используем эти индексы при ожидаемом на следующий год спросе в 1100 единиц.
Тогда прогнозируемый спрос будет таким.
Ожидаемый
спрос на
следующий год
Средний уро- вень продаж
за каждый сезон (1100/4)
Сезонный
индекс
Сезонный прогноз
на следующий год
Весна 275
X
0,8 = 220
Лето 275
X
1,4 = 385
Осень 275
X
1,2 = 330
Зима 275
X
0,6 =
165
Сумма 1100
Сезонный фактор может периодически обновляться по мере получения новой
информации. В следующем примере определяются сезонные индексы и
мультипликативные сезонные колебания.
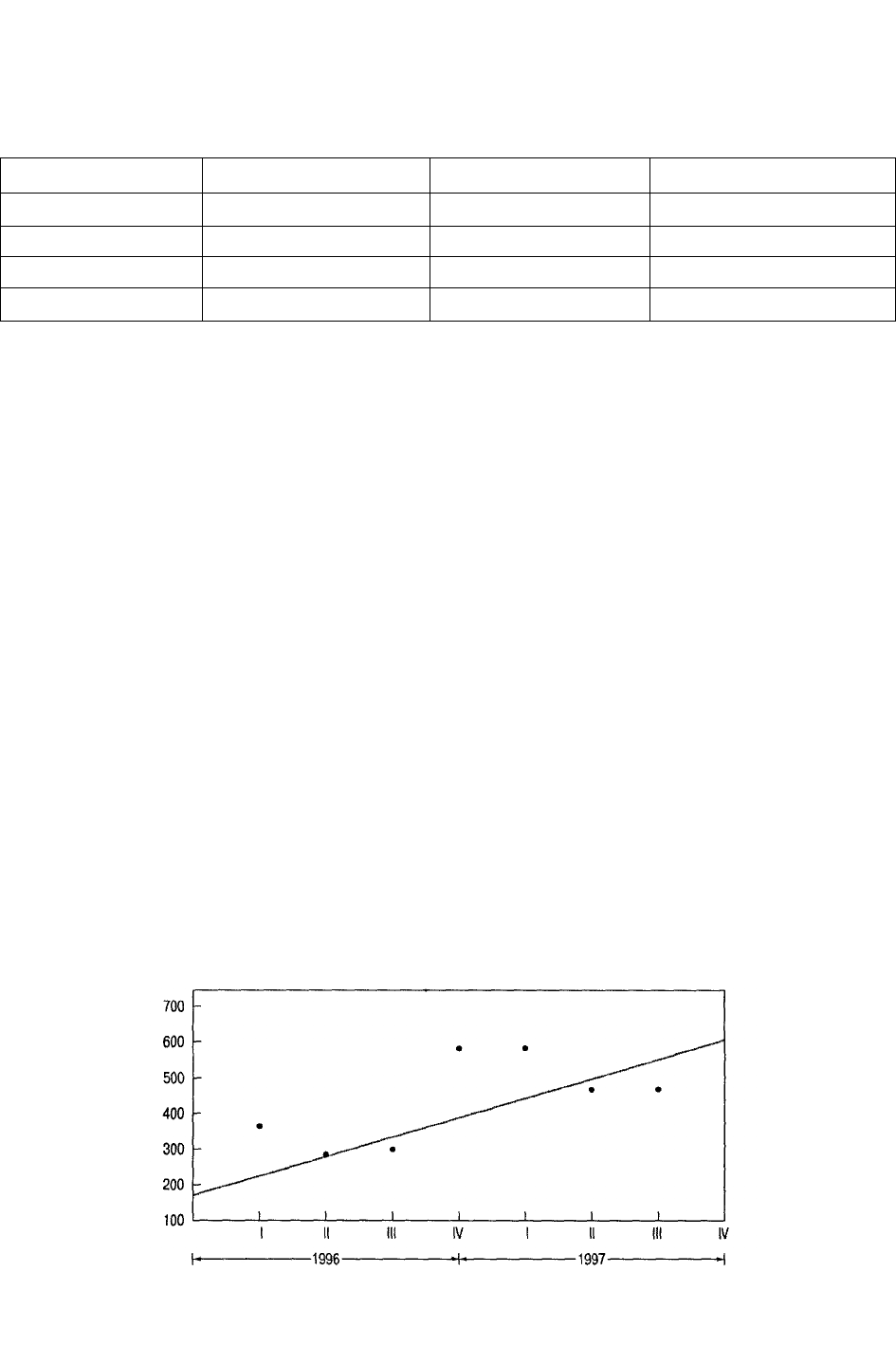
Пример 13.4. Вычисление тренда и сезонного индекса по графику, построенному
ручной аппроксимацией
В этом примере определим тренд и сезонные индексы.
567
Решение
Решим эту задачу, построив прямую линию способом ручной аппроксимации точек
данных. После этого найдем по графику тренд и величину отсекаемого отрезка прямой.
Предположим, что данные предыдущего периода были такими.
Квартал Количество Квартал Количество
1 — 1996 300 I — 1997 520
II — 1996 200 II— 1997 420
III — 1996 220 III —1997 400
IV—1996 530 IV—1997 700
Нанесем точки на координатную сетку, как показано на рис. 13.10, а затем проведем
прямую линию. (Эта линия и вытекающее из нее уравнение необходимы для определения
отклонений.) Уравнение этой линии будет иметь такой вид:
Тренд
t
= 170 + 55t.
Это уравнение получено при величине отсекаемого отрезка, равного 170, плюс
прирост на (670— 170)/8 периодов. Дальше можно определить сезонный индекс,
сравнивая текущие данные с трендовой линией, что приведено на рис. 13.11. При этом
сезонный индекс определяется усреднением сезонных индексов одинаковых кварталов
каждого года.
Теперь можно вычислить прогноз на 1998 год с учетом тренда и сезонных факторов
(Forecast Including Trend and Seasonal factor — FITS ):
FITS
t
= Тренд x Сезонный фактор.
I квартал 1998: FITS
9
= (170 + 55 x 9) x 1,25 = 831;
II квартал 1998: F/TS
10
= (170 + 55 x 10) x 0,78 = 562;
III квартал 1998: F/TS
11
= (170 + 55 x 11) x 0,69 = 535; IV квартал 1998: FITS
12
= (170
+ 55 x 12) x 1,25= 1038.
Разложение с использованием регрессионного анализа методом наименьших
квадратов. Разложение временного ряда означает нахождение основных компонентов
ряда: трендовых, сезонных и циклических. В процессе разложения определяют индексы
сезонности и цикличности. Затем процедура прогнозирования предусматривает
определение параметров тренда, продолжение его в будущие периоды и его
корректировку с помощью сезонных и циклических индексов, которые были определены в
процессе разложения.
Рис. 13.10. График поквартального спроса
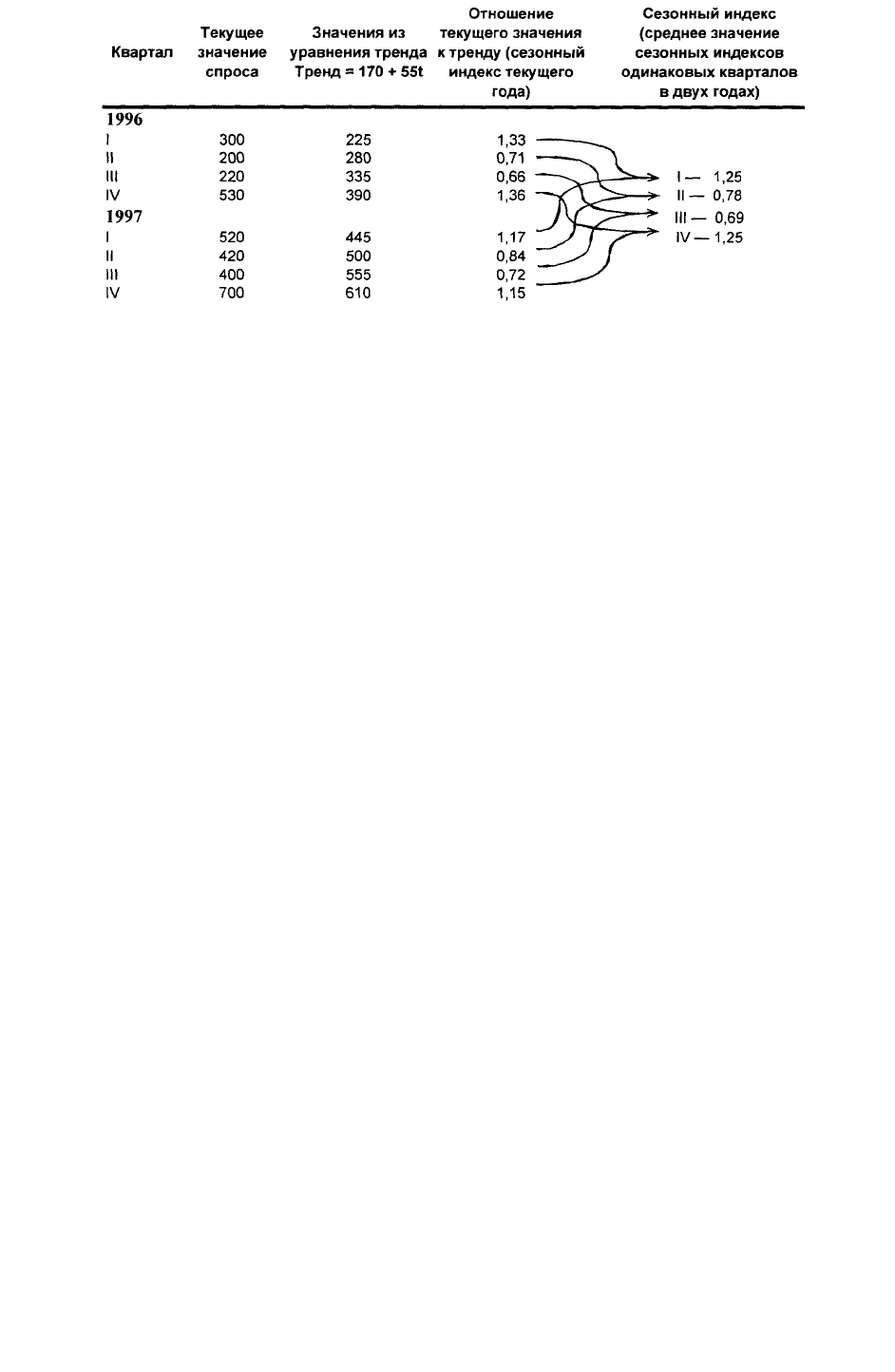
568
Рис. 13.11. Определение сезонного индекса по текущим данным и тренду
Последовательность процесса декомпозиции
1. Разложение временного ряда на компоненты:
a) определение сезонного компонента;
b) устранение сезонного влияния на спрос;
c) определение трендовой компоненты.
2. Составление прогноза будущих значений по каждому компоненту.
a) распространение трендового компонента на будущие периоды;
b) умножение трендового компонента на сезонный.
Следует отметить, что в этот перечень этапов не включен случайный компонент,
который неявно удаляется из временного ряда при усреднении на первом этапе.
Бессмысленно пытаться планировать случайный компонент на втором этапе, не имея
информации о непредвиденных событиях, например, о серьезном трудовом конфликте
между рабочими и предпринимателями, который может неблагоприятно повлиять на
спрос товара.
В табл. 13.7 показано разложение временного ряда с использованием регрессионного
анализа на основе метода наименьших квадратов и исходных данных ранее
рассмотренных примеров. Каждая точка данных соответствует одному кварталу в
трехгодичном периоде (12 кварталов). Задача заключается в прогнозировании спроса на
четыре квартала четвертого года.
Этап 1. Определение сезонного индекса. В табл. 13.7 приведены все необходимые
вычисления. В колонку 4 включены средние значения данного квартала за трехлетний
период, т.е. данные каждого квартала каждого из трех лет просуммировали и разделили на
три. Сезонный индекс получают делением этого среднего значения на общее среднее
значение для всех 12 кварталов (33 350/12 = = 2779,2). Сезонные индексы включены в
колонку 5. Следует отметить, что сезонные индексы имеют одинаковое значение для
одноименных кварталов каждого года.
Этап 2. Устранение сезонного влияния на исходные данные. Его результаты
показаны в колонке 6 табл. 13.7 (y
d
— спрос без учета сезонного влияния).
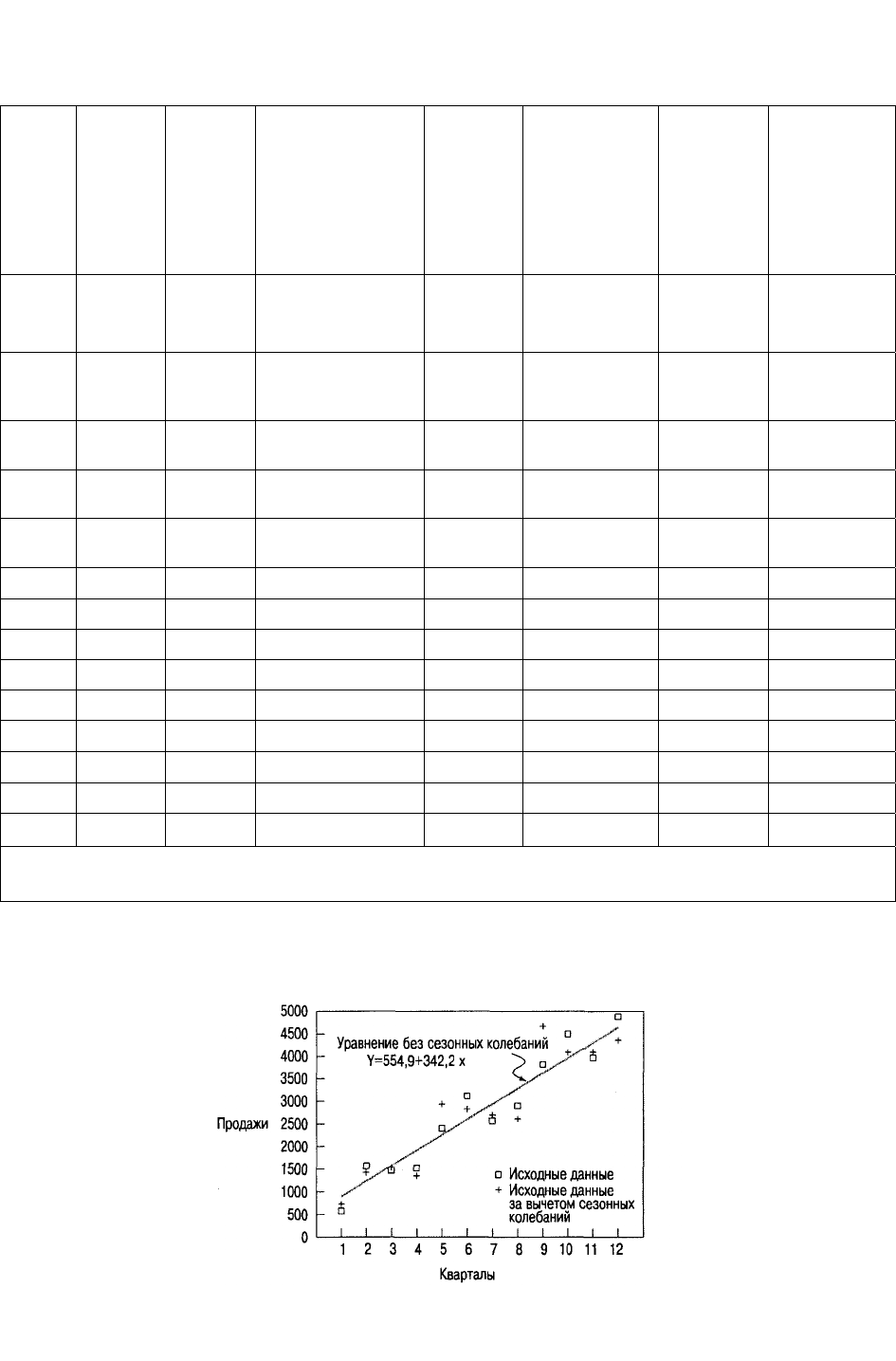
Этап 3. Построение линии регрессии методом наименьших квадратов для
устранения сезонного влияния на исходные данные. Целью данного этапа является
получение уравнения для трендовой линии Y:
Y =а + bх,
где х — квартал;
Y — спрос, вычисленный с использованием уравнения регрессии Y = а + bх;
а — величина отрезка, отсекаемого на оси Y; b — коэффициент наклона прямой.
569
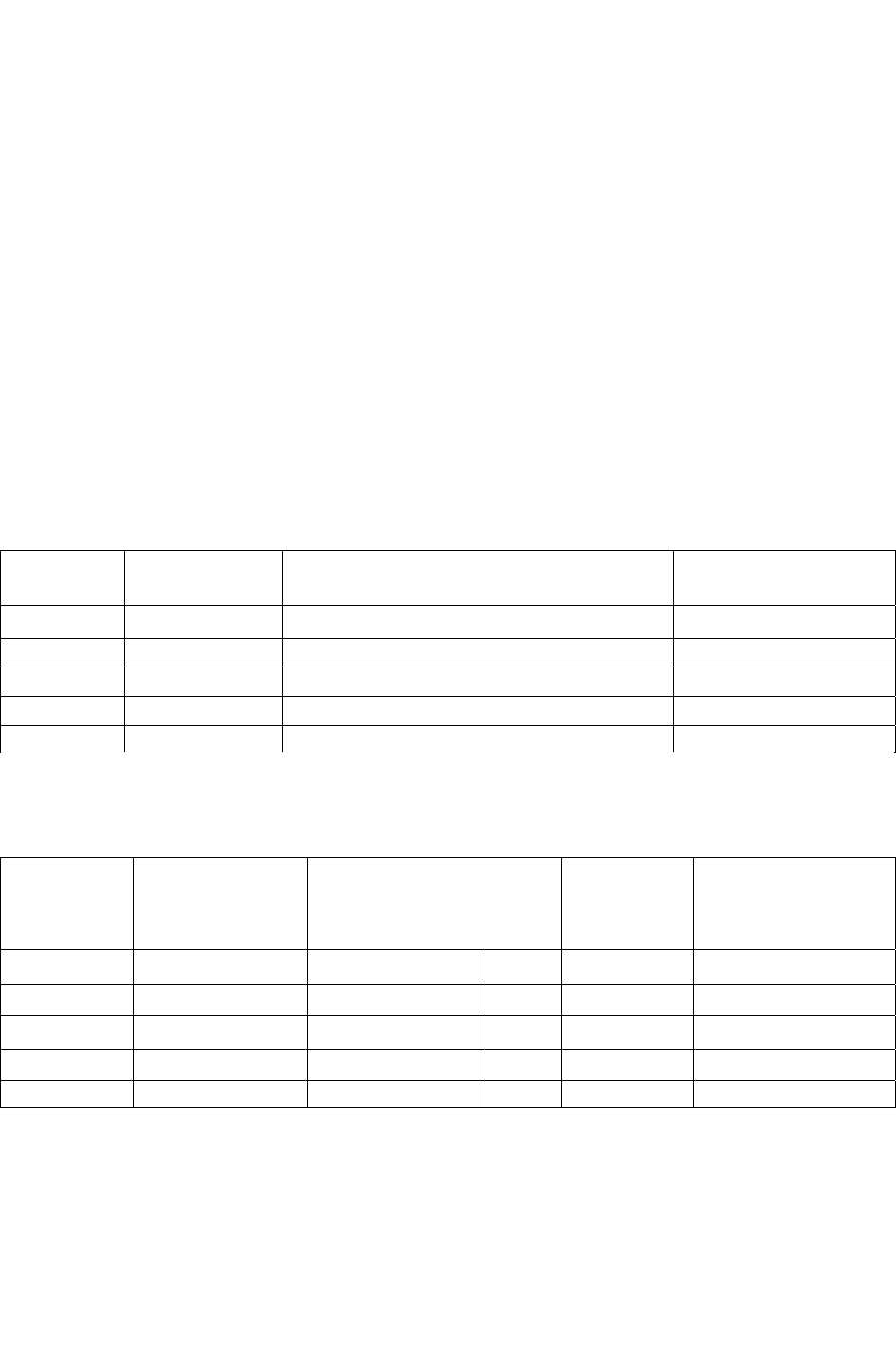
Таблица 13.7. Устранение сезонного влияния на спрос
Период
(x)
Квартал
Текущий
спрос (у)
Средний спрос
данного
квартала за все
три года
Сезонный
индекс
Спрос без
учета
сезонного
влияния (у
d
(Колонка 3,
деленная на
колонку 5)
х
2
(Колонка
1)
2
х х у
d
(Колонка 1,
умноженная
на колонку
6)
1 2 3 4 5 6 7 8
1 I 600
(600 + 2400
+3800)/3 = 2266,7
0,82 735,7 1 735,7
2 II 1550
(1550 + 3100 +
4500)/3 = 3050
1,10 1412,4 4 2824,7
3 III 1500
(1500 + 2600 +
4000)/3 = 2700
0,97 1544,0 9 4631,9
4 IV 1500
(1500 + 2900 +
4900)/3 = 3100
1,12 1344,8 16 5379,0
5 2400 0,82 2942,6 25 14 713,2
6 II 3100 1,10 2824,7 36 16 948,4
7 III 2600 0,97 2676,2 49 18 733,6
8 IV 2900 1,12 2599,9 64 20 798,9
9 3800 0,82 4659,2 81 41 932,7
10 II 4500 1,10 4100,4 100 41 004,1
11 III 4000 0,97 4117,3 121 45 290,1
12 IV 4900 1,12 4392,9 144 52 714,5
78 33 350 12,03 33 350,1* 650 265 706,9
Y-
78
-
65
- ь-^хУч-ПхУ" _265706,9-(1'2х6,5х2779,2)_
31ОО
. 12 ' ' Х*
2
-"*
2
650-(12х6,5
2
) ' '
y
d
= 33350/12 = 2779,2 ; a = ~y
d
-bx = 2779,2-342,2x6,5 = 554,9 ; Y = a + bx = 554,9 + 342,2х.
*Суммы в колонках 3 и 6 должны быть одинаковыми и равными 33 350. Разница возникла из-за
округления чисел, которое в колонке 5 выполнено с точностью до сотых.
Рис. 13.12. Тренд с исключенным влиянием сезонных колебаний спроса
570
Вычисление значений наименьших квадратов с использованием данных колонок 1, 7
и 8 показано в нижней части табл. 13.7. Окончательное уравнение, с устраненным
влиянием сезонного фактора, принимает такой вид: Y =а + bх = 554,9 + 342,2х . Эта
прямая показана на рис. 13.12.
Этап 4. Распространение линии регрессии на прогнозируемый период. Целью
данного этапа является составление прогнозов на кварталы 13—16. Задачу начинают с
решения уравнения относительно Y для каждого из этих периодов. Результаты показаны в
третьей колонке таблицы расчетов пятого этапа.
Этап 5. Разработка окончательного прогноза корректировкой линии регрессии
сезонными индексами. Следует вспомнить, что в уравнении Y = а + bх был исключен
сезонный фактор. А теперь следует проделать обратную процедуру, умножив значения
квартальных данных на значение сезонного индекса данного квартала.
Период Квартал
Y, полученный из
линии регрессии
Сезонный индекс
Прогноз (Yx
Сезонный
индекс)
13 I 5003,5 0,82 4102,87
14 II 5345,7 1,10 5880,27
15 III 5687,9 0,97 5517,26
16 IV 6030,1 1,12 6753,71
Составление прогноза завершено. Процедура, в основном, аналогична
использованной в предыдущем примере ручной аппроксимации. Однако в последнем
примере мы следовали более формализованной процедуре и вычислили линию регрессии
методом наименьших квадратов.
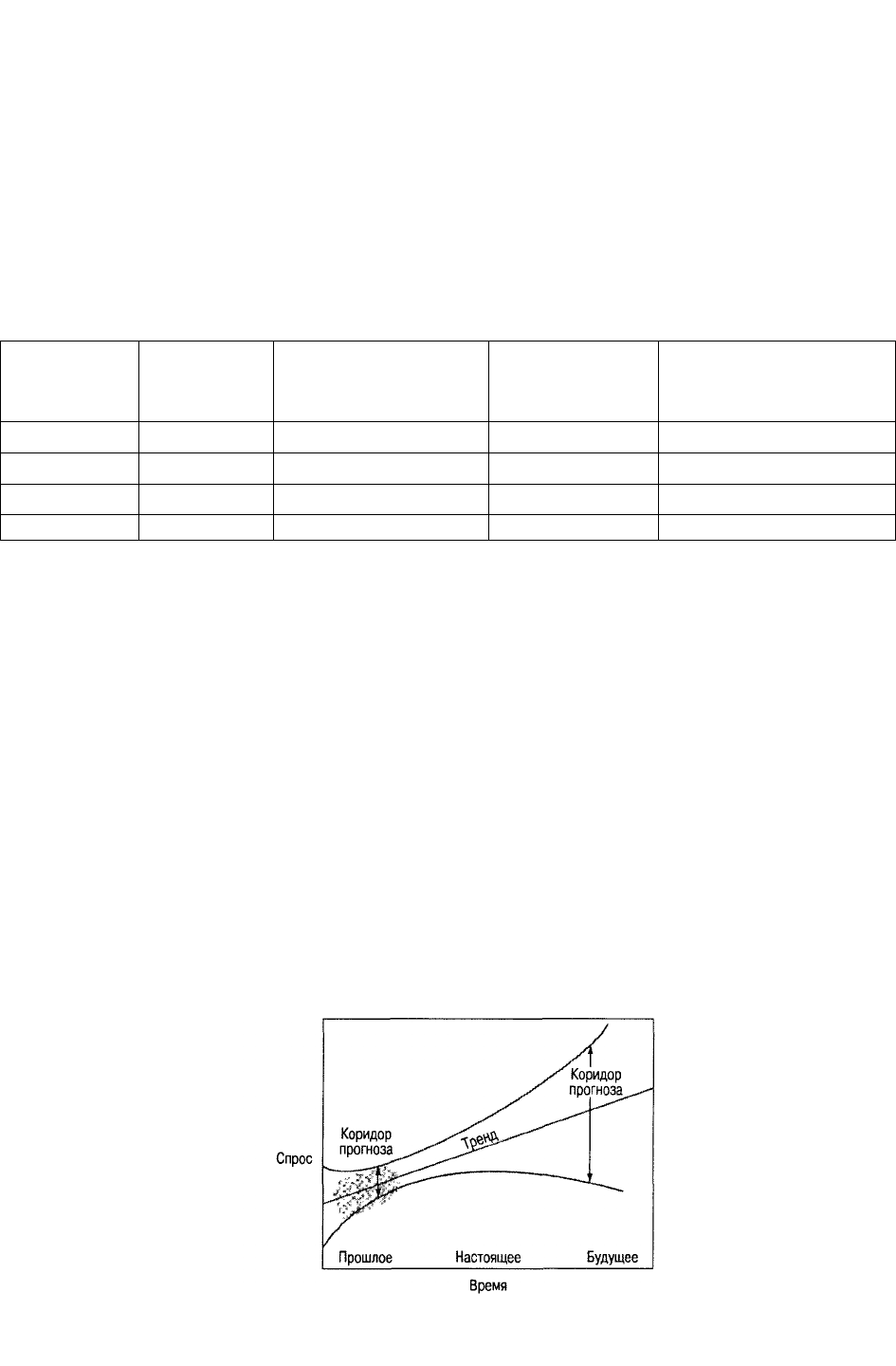
Диапазон ошибки. В процессе подгонки прямой линии под исходные данных и
использовании ее для прогнозирования возможны два источника появления ошибок. Во-
первых, существуют обычные ошибки, описываемые стандартным отклонением любого
набора данных. Во-вторых, возможны ошибки построения линии. На рис. 13.13 показан
коридор возможных ошибок прогнозирования.
Не приводя статистику, кратко поясним причины расширения коридора ошибок.
Сначала мысленно представьте себе, что верхняя граница коридора содержит ошибку,
увеличивающую крутизну линии, а затем предположите, что другая граница имеет
противоположную ошибку, т.е. линия загибается вниз. Общий интервал ошибки в таком
случае будет включать ошибки построения обеих граничных линий, впрочем, как и
ошибки построения самого тренда. В результате действия противоположно направленных
ошибок коридор прогноза расширяется в будущем.
Рис. 13.13. Коридор прогноза для линейного тренда
