Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.


and, with p q, a 1 v, this can be written
ÿp q1 v
ÿpÿq
Z
1
0
e
ÿ1vt
t
pqÿ1
dt:
Multiplying by v
pÿ1
and integrating with respect to v between 0 and 1 ,
ÿp q
Z
1
0
v
pÿ1
1 v
ÿpÿq
dv
Z
1
0
v
pÿ1
dv
Z
1
0
e
ÿ1vt
t
pq1
dt:
Then interchanging the order of integration in the double integral on the right and
using Eq. (2.42),
ÿp qBp; q
Z
1
0
e
ÿt
t
pqÿ1
dt
Z
1
0
e
ÿvt
v
pÿ1
dv
Z
1
0
e
ÿt
t
pqÿ1
ÿp
t
p
dt; using Eq: 2:44
ÿp
Z
1
0
e
ÿt
t
qÿ1
dt ÿpÿq:
Example 2.15
Evaluate the integral
Z
1
0
3
ÿ4x
2
dx:
Solution: We ®rst notice that 3 e
ln 3
, so we can rewrite the integral as
Z
1
0
3
ÿ4x
2
dx
Z
1
0
e
ln 3
ÿ4x
2
dx
Z
1
0
e
ÿ4ln3x
2
dx:
Now let (4 ln 3)x
2
z, then the integral becomes
Z
1
0
e
ÿz
d
z
1=2
4ln3
p
ý!
1
2
4ln3
p
Z
1
0
z
ÿ1=2
e
ÿz
dz
ÿ
1
2
2
4ln3
p
p
2
4ln3
p
:
Problems
2.1 Solve the following equations:
(a) xdy=dx y
2
1;
(b) dy=dx x y
2
.
2.2 Melting of a sphere of ice: Assume that a sphere of ice melts at a rate
proportional to its surface area. Find an expression for the volume at any
time t.
2.3 Show that 3x
2
y cos xdx sin x ÿ 4y
3
dy 0 is an exact diÿerential
equation and ®nd its general solution.
96
ORDINARY DIFFERENTIAL EQUATIONS

2.4 RC circuits: A typical RC circuit is shown in Fig. 2.3. Find current ¯ow It
in the circuit, assuming EtE
0
.
Hint: the voltage drop across the capacitor is given Q/C, with Q(t) the
charge on the capacitor at time t.
2.5 Find a constant such that x y
is an integrati ng factor of the equation
4x
2
2xy 6ydx 2x
2
9y 3xdy 0:
What is the solution of this equation?
2.6 Solve dy=dx y y
3
x:
2.7 Solve:
(a) the equation D
2
ÿ D ÿ 12y 0 with the boundary conditions y 0,
Dy 3 when t 0;
(b) the equation D
2
2D 3y 0 with the boundary conditions y 2,
Dy 0 when t 0;
(c) the equation D
2
ÿ 2D 1y 0 with the boundary conditions y 5,
Dy 3 when t 0.
2.8 Find the particular integral of D
2
2D ÿ 1y 3 t
3
.
2.9 Find the particular integral of 2D
2
5D 73e
2t
.
2.10 Find the particular integral of 3D
2
D ÿ 5y cos 3t:
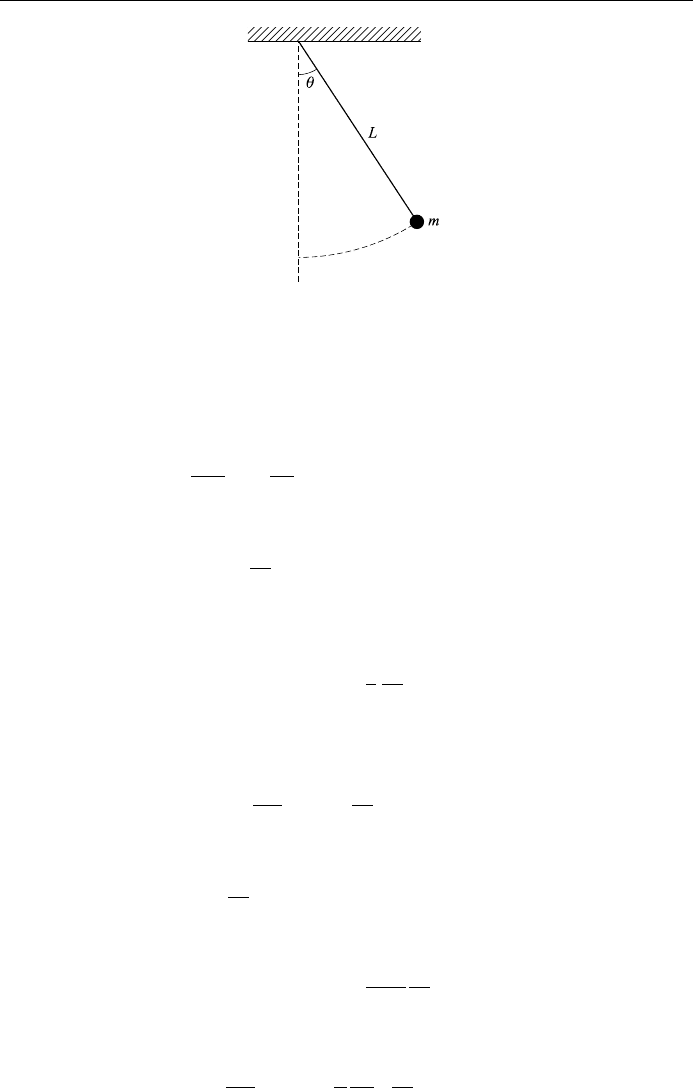
2.11 Simple harmonic motion of a pendulum (Fig. 2.4): Suspend a ball of mass m
at the end of a massless rod of length L and set it in motion swinging back
and forth in a vertical plane. Show that the equation of motion of the ball is
d
2
dt
2
g
L
sin 0;
where g is the local gravitational acceleration. Solve this pendulum equation
for small displacements by replacing sin by .
2.12 Forced oscillations with damping: If we allow an external driving force Ft
in addition to damping (Example 2.12), the motion of the oscillator is
governed by
y
00
b
m
y
0
k
m
y F t;
97
PROBLEMS
Figure 2.3. RC circuit.
a constant coecient non-homogeneous equation. Solve this equation for
FtA cos!t:
2.13 Solve the equation
r
2
d
2
R
dr
2
2r
dR
dr
ÿ nn 1R 0 n constant:
2.14 The ®rst-order non-linear equation
dy
dx
y
2
Qxy Rx0
is known as Riccati's equation. Show that, by use of a change of dependent
variable
y
1
z
dz
dx
;
Riccati's equation transforms into a second-order linear diÿerential equa-
tion
d
2
z
dx
2
Qx
dz
dx
Rxz 0:
Sometimes Riccati's equ ation is written as
dy
dx
Pxy
2
Qxy Rx0:
Then the transformation becomes
y ÿ
1
Px
dz
dx
and the second-order equation takes the form
d
2
z
dx
2
Q
1
P
dP
dx
dz
dx
PRz 0:
98
ORDINARY DIFFERENTIAL EQUATIONS
Figure 2.4. Simple pendulum.

2.15 Solve the equation 4x
2
y
00
4xy
0
x
2
ÿ 1y 0 by using Frobenius'
method, wher e y
0
dy=dx,andy
00
d
2
y=dx
2
.
2.16 Find a series solution, valid for large values of x, of the equation
1 ÿ x
2
y
00
ÿ 2xy
0
2y 0:
2.17 Show that a series solution of Airy's equation y
00
ÿ xy 0is
y a
0
1
x
3
2 3
x
6
2 3 5 6
ý!
b
0
x
x
4
3 4
x
7
3 4 6 7
ý!
:
2.18 Show that Weber's equation y
00
n
1
2
ÿ
1
4
x
2
y 0 is reduced by the sub-
stitution y e
ÿx
2
=4
v to the equation d
2
v=dx
2
ÿ xdv=dxnv 0. Show
that two solutions of this latter equation are
v
1
1 ÿ
n
2!
x
2
nn ÿ 2
4!
x
4
ÿ
nn ÿ 2n ÿ 4
6!
x
6
ÿ;
v
2
x ÿ
n ÿ 1
3!
x
3
n ÿ 1n ÿ 3
5!
x
5
ÿ
n ÿ 1n ÿ 3n ÿ 5
7!
x
7
ÿ:
2.19 Solve the following simultaneous equations
Dx y t
3
Dy ÿ x t
)
D d=dt:
2.20 Evaluate the integrals:
(a)
Z
1
0
x
3
e
ÿx
dx:
(b)
Z
1
0
x
6
e
ÿ2x
dx hint: let y 2x:
(c)
Z
1
0
y
p
e
ÿy
2
dy hint: let y
2
x:
(d)
Z
1
0
dx
ÿln x
p
hint : let ÿ ln x u:
2.21 (a) Pr ove that Bp; q2
Z
=2
0
sin
2pÿ1
cos
2qÿ1
d.
(b) Evaluate the integral
Z
1
0
x
4
1 ÿ x
3
dx:
2.22 Show that n!
2n
p
n
n
e
ÿn
. This is known as Stirling's factorial approxima-
tion or asymptotic formula for n!.
99
PROBLEMS

3
Matrix algebra
As vector methods have become standard tools for physicists, so too matrix
methods are becoming very useful tools in sciences and engineering. Matrices
occur in physics in at least two ways: in handling the eigenvalue problems in
classical and quantum mechanics, and in the solutions of systems of linear equa-
tions. In this chapter, we introduce matrices and related concepts, and de®ne some
basic matrix algebra. In Chapter 5 we will discuss various operations with
matrices in dealing with transformations of vectors in vector spaces and the
operation of linear operators on vector spaces.
De®nition of a matrix
A matrix consists of a rectangular block or ordered array of numbers that obeys
prescribed rules of addition and multiplication. The numbers may be real or
complex. The array is usually enclosed within curved brackets. Thus
124
2 ÿ17
is a matrix consisting of 2 rows and 3 columns, and it is called a 2 3(2by3)
matrix. An m n matrix consists of m rows and n columns, which is usually
expressed in a double sux notation:
~
A
a
11
a
12
a
13
a
1n
a
21
a
22
a
23
... a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
m3
... a
mn
0
B
B
B
B
@
1
C
C
C
C
A
: 3:1
Each number a
ij
is called an element of the matrix, where the ®rst subscript i
denotes the row, while the second subscript j indicates the column. Thus, a
23
100

refers to the element in the second row and third column. The element a
ij
should
be distinguished from the element a
ji
.
It should be pointed out that a matrix has no single numerical value; therefore it
must be carefully distinguished from a determinant.
We will denote a matrix by a letter with a tilde over it, such as
~
A in (3.1).
Sometimes we write (a
ij
)or(a
ij
mn
, if we wish to express explicitly the particular
form of element contained in
~
A.
Although we hav e de®ned a matrix here with reference to numbers, it is easy to
extend the de®nition to a matrix whose elements are functions f
i
x; for a 2 3
matrix, for example, we have
f
1
x f
2
x f
3
x
f
4
x f
5
x f
6
x
:
A matrix having only one row is called a row matrix or a row vector, while a
matrix having only one column is called a column matrix or a column vector. An
ordinary vector A A
1
^
e
1
A
2
^
e
2
A
3
^
e
3
can be represented either by a row
matrix or by a column matrix.
If the numbers of rows m and columns n are equal, the matrix is called a square
matrix of order n.
In a square matrix of order n, the elements a
11
; a
22
; ...; a
nn
form what is called
the principal (or leading) diagonal, that is, the diagonal from the top left hand
corner to the bottom right hand corner. The diagonal from the top right hand
corner to the bottom left hand corner is sometimes termed the trailin g diagonal.
Only a square matrix possesses a principal diagonal and a trailing diagonal.
The sum of all elements down the principal diagonal is called the trace, or spur,
of the matrix. We write
Tr
~
A
X
n
i1
a
ii
:
If all elements of the principal diagonal of a square matrix are unity while all
other elements are zero, then it is called a unit matrix (for a reason to be explained
later) and is denoted by
~
I. Thus the unit matrix of order 3 is
~
I
100
010
001
0
B
@
1
C
A
:
A square matrix in which all elements other than those along the principal
diagonal are zero is called a diagonal matrix.
A matrix with all elements zero is known as the null (or zero) matrix and is
denoted by the symbol
~
0, since it is not an ordinary number, but an array of zeros.
101
DEFINITION OF A MATRIX

Four basic algebra operations for matrices
Equality of matrices
Two matrices
~
A a
jk
and
~
B b
jk
are equal if and only if
~
A and
~
B have the
same order (equal numbers of rows and columns) and corresponding elements are
equal, that is
a
jk
b
jk
for all j and k:
Then we write
~
A
~
B:
Addition of matrices
Addition of matrices is de®ned only for matrices of the same order. If
~
A a
jk
and
~
B b
jk
have the same order, the sum of
~
A and
~
B is a matrix of the same
order
~
C
~
A
~
B
with elements
c
jk
a
jk
b
jk
: 3:2
We see that
~
C is obtained by adding corresponding elements of
~
A and
~
B.
Example 3.1
If
~
A
214
302
;
~
B
35 1
21ÿ3
hen
~
C
~
A
~
B
214
302
ý!
35 1
21ÿ3
ý!
2 31 54 1
3 20 12ÿ 3
ý!
56 5
51ÿ1
ý!
:
From the de®nitions we see that matrix addition obeys the commutative and
associative laws, that is, for any matrices
~
A,
~
B,
~
C of the same order
~
A
~
B
~
B
~
A;
~
A
~
B
~
C
~
A
~
B
~
C: 3:3
Similarly, if
~
A a
jk
and
~
B b
jk
) have the same order, we de®ne the diÿer-
ence of
~
A and
~
B as
~
D
~
A ÿ
~
B
102
MATRIX ALGEBRA

with elements
d
jk
a
jk
ÿ b
jk
: 3:4
Multiplication of a matrix by a number
If
~
A a
jk
and c is a number (or scalar), then we de®ne the product of
~
A and c as
c
~
A
~
Ac ca
jk
; 3:5
we see that c
~
A is the matrix obtained by multiplying each elemen t of
~
A by c.
We see from the de®nition that for any matrices and any numbers,
c
~
A
~
Bc
~
A c
~
B; c k
~
A c
~
A k
~
A; ck
~
Ack
~
A: 3:6
Example 3.2
7
abc
def
7a 7b 7c
7d 7e 7f
:
Formulas (3.3) and (3.6) express the properties which are characteristic for a
vector space. This gives vector spaces of matrices. We will discus s this further in
Chapter 5.
Matrix multiplication
The matrix product
~
A
~
B of the matrices
~
A and
~
B is de®ned if and only if the
number of columns in
~
A is equal to the number of rows in
~
B. Such matrices
are sometimes called `conformable'. If
~
A a
jk
is an n s matrix and
~
B b
jk
is an s m matrix, then
~
A and
~
B are conformable and their matrix
product, written
~
C
~
A
~
B,isann m matrix formed according to the rule
c
ik
X
s
j1
a
ij
b
jk
; i 1; 2; ...; nk 1; 2; ...; m: 3:7
Consequently, to determine the ijth element of matrix
~
C, the corresponding terms
of the ith row of
~
A and jth column of
~
B are multiplied and the resulting products
added to form c
ij
.
Example 3.3
Let
~
A
214
ÿ302
;
~
B
35
2 ÿ1
42
0
B
@
1
C
A
103
FOUR BASIC ALGEBRA OPERATIONS FOR MATRICES

then
~
A
~
B
2 3 1 2 4 42 5 1 ÿ14 2
ÿ33 0 2 2 4 ÿ35 0 ÿ12 2
ý!
24 17
ÿ1 ÿ11
ý!
:
The reader should master matrix multiplication, since it is used throughout the
rest of the book.
In general, matrix multiplication is not commutative:
~
A
~
B 6
~
B
~
A. In fact,
~
B
~
A is
often not de®ned for non-square matrices, as shown in the following example.
Example 3.4
If
~
A
12
34
ý!
;
~
B
3
7
ý!
then
~
A
~
B
12
34
3
7
1 3 2 7
3 3 4 7
17
37
:
But
~
B
~
A
3
7
12
34
is not de®ned.
Matrix multiplication is associative and distributive:
~
A
~
B
~
C
~
A
~
B
~
C;
~
A
~
B
~
C
~
A
~
C
~
B
~
C:
To prove the associative law, we start with the matrix product
~
A
~
B, then multi-
ply this product from the right by
~
C:
~
A
~
B
X
k
a
ik
b
kj
;
~
A
~
B
~
C
X
j
X
k
a
ik
b
kj
ý!
c
js
"#
X
k
a
ik
X
j
b
kj
c
js
ý!
~
A
~
B
~
C:
Products of matrices diÿer from products of ordinary numbers in many
remarkable ways. For example,
~
A
~
B 0 does not imply
~
A 0or
~
B 0. Even
more bizarre is the case where
~
A
2
0,
~
A 6 0; an example of which is
~
A
01
00
:
104
MATRIX ALGEBRA

When you ®rst run into Eq. (3.7), the rule for matrix multiplication, you might
ask how anyone would arrive at it. It is suggested by the use of matrices in
connection with linear transformations. For simplicity, we consider a very simple
case: three coordinates systems in the plane denoted by the x
1
x
2
-system, the y
1
y
2
-
system, and the z
1
z
2
-system. We assume that these systems are related by the
following linear transformations
x
1
a
11
y
1
a
12
y
2
; x
2
a
21
y
1
a
22
y
2
; 3:8
y
1
b
11
z
1
b
12
z
2
; y
2
b
21
z
1
b
22
z
2
: 3:9
Clearly, the x
1
x
2
-coordinates can be obtained directly from the z
1
z
2
-coordinates
by a single linear transformation
x
1
c
11
z
1
c
12
z
2
; x
2
c
21
z
1
c
22
z
2
; 3:10
whose coecients can be found by inserting (3.9) into (3.8),
x
1
a
11
b
11
z
1
b
12
z
2
a
12
b
21
z
1
b
22
z
2
;
x
2
a
21
b
11
z
1
b
12
z
2
a
22
b
21
z
1
b
22
z
2
:
Comparing this with (3.10), we ®nd
c
11
a
11
b
11
a
12
b
21
; c
12
a
11
b
12
a
12
b
22
;
c
21
a
21
b
11
a
22
b
21
; c
22
a
21
b
12
a
22
b
22
;
or brie¯y
c
jk
X
2
i1
a
ji
b
ik
; j; k 1; 2; 3:11
which is in the form of (3.7).
Now we rewrite the transformations (3.8), (3.9) and (3.10) in matrix form:
~
X
~
A
~
Y;
~
Y
~
B
~
Z; and
~
X
~
C
~
Z;
where
~
X
x
1
x
2
ý!
;
~
Y
y
1
y
2
ý!
;
~
Z
z
1
z
2
ý!
;
~
A
a
11
a
12
a
21
a
22
ý!
;
~
B
b
11
b
12
b
21
b
22
ý!
; C
:::
c
11
c
12
c
21
c
22
ý!
:
We then see that
~
C
~
A
~
B, and the elements of
~
C are given by (3.11).
Example 3.5
Rotations in three-dimensional space: An example of the use of matrix multi-
plication is provided by the representation of rotations in three-dimensional
105
FOUR BASIC ALGEBRA OPERATIONS FOR MATRICES
