Chow T.L. Mathematical Methods for Physicists: A Concise Introduction
Подождите немного. Документ загружается.

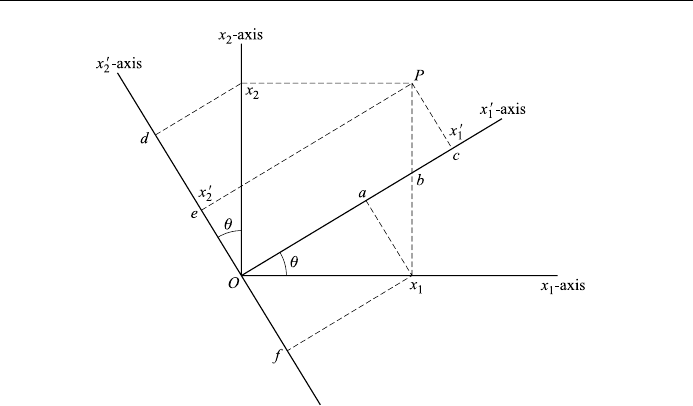
space. In Fig. 3.1, the primed coordinates are obtained from the unprimed coor-
dinates by a rotation through an angle about the x
3
-axis. We see that x
0
1
is the
sum of the projection of x
1
onto the x
0
1
-axis and the projection of x
2
onto the x
0
1
-
axis:
x
0
1
x
1
cos x
2
cos=2 ÿ x
1
cos x
2
sin ;
similarly
x
0
2
x
1
cos=2 x
2
cos ÿx
1
sin x
2
cos
and
x
0
3
x
3
:
We can put these in matrix form
X
0
R
X;
where
X
0
x
0
1
x
0
2
x
0
3
0
B
@
1
C
A
; X
x
1
x
2
x
3
0
B
@
1
C
A
; R
cos sin 0
ÿsin cos 0
001
0
B
@
1
C
A
:
106
MATRIX ALGEBRA
Figure 3.1. Coordinate changes by rotation.

The commutator
Even if matrices
~
A and
~
B are both square matrices of order n, the products
~
A
~
B
and
~
B
~
A, although both square matrices of order n, are in general quite diÿerent,
since their individual elements are formed diÿerently. For example,
12
13
10
12
34
46
but
10
12
12
13
12
38
:
The diÿerence between the two products
~
A
~
B and
~
B
~
A is known as the commu-
tator of
~
A and
~
B and is denoted by
~
A;
~
B
~
A
~
B ÿ
~
B
~
A: 3:12
It is obvious that
~
B;
~
Aÿ
~
A;
~
B: 3:13
If two square matrices
~
A and
~
B are very carefully chosen, it is possible to make the
product identical. That is
~
A
~
B
~
B
~
A. Two such matrices are said to commute with
each other. Commuting matrices play an important role in quantum mechanics.
If
~
A commutes with
~
B and
~
B commutes with
~
C, it does not necessarily follow
that
~
A commutes with
~
C.
Powers of a matrix
If n is a positive integer and
~
A is a square matrix, then
~
A
2
~
A
~
A,
~
A
3
~
A
~
A
~
A, and
in general ,
~
A
n
~
A
~
A
~
A (n times). In particular,
~
A
0
~
I.
Functions of matrices
As we de®ne and study various functions of a variable in algebra, it is possible to
de®ne and evaluate functions of matrices. We shall brie¯y discuss the following
functions of matrices in this section: integral powers and exponentia l.
A simple example of integral powers of a matrix is polynomials such as
f
~
A
~
A
2
3
~
A
5
:
Note that a matrix can be multiplied by itself if and only if it is a square matrix.
Thus
~
A here is a square matrix and we denote the product
~
A
~
A as
~
A
2
. More fancy
examples can be obtained by taking series, such as
~
S
X
1
k0
a
k
~
A
k
;
where a
k
are scalar coecients. Of course, the sum has no meaning if it does not
converge. The convergence of the matrix series means every matrix element of the
107
THE COMMUTATOR

in®nite sum of matrices converges to a limit. We will not discuss the general
theory of convergence of matr ix functions. Another very common series is de®ned
by
e
~
A
X
1
n0
~
A
n
n!
:
Transpose of a matrix
Consider an m n matrix
~
A, if the rows and columns are systematically changed
to columns to rows, without changing the order in which they occur, the new
matrix is called the transpose of matrix
~
A. It is denoted by
~
A
T
:
~
A
a
11
a
12
a
13
... a
1n
a
21
a
22
a
23
... a
2n
.
.
.
.
.
.
.
.
.
.
.
.
a
m1
a
m2
a
m3
... a
mn
0
B
B
B
B
@
1
C
C
C
C
A
;
~
A
T
a
11
a
21
a
31
... a
m1
a
12
a
22
a
32
... a
m2
.
.
.
.
.
.
.
.
.
.
.
.
a
n1
a
2n
a
3n
... a
mn
0
B
B
B
B
@
1
C
C
C
C
A
:
Thus the transpose matrix has n rows and m columns. If
~
A is written as (a
jk
), then
~
A
T
may be written as a
kj
).
~
A a
jk
;
~
A
T
a
kj
: 3:14
The transpose of a row matrix is a column matrix, and vice versa.
Example 3.6
~
A
123
456
;
~
A
T
14
25
36
0
B
@
1
C
A
;
~
B 123;
~
B
T
1
2
3
0
B
@
1
C
A
:
It is obvious that
~
A
T
T
~
A,and
~
A
~
B
T
~
A
T
~
B
T
. It is also easy to prove
that the transpose of the product is the product of the transposes in reverse:
~
A
~
B
T
~
B
T
~
A
T
: 3:15
Proof:
~
A
~
B
T
ij
~
A
~
B
ji
by definition
X
k
A
jk
B
ki
X
k
B
T
ik
A
T
kj
~
B
T
~
A
T
ij
108
MATRIX ALGEBRA

so that
AB
T
B
T
A
T
q:e:d:
Because of (3.15), even if
~
A
~
A
T
and
~
B
~
B
T
,
~
A
~
B
T
6
~
A
~
B unless the matrices
commute.
Symmetric and skew-symmetric matrices
A square matrix
~
A a
jk
is said to be symmetric if all its elements satisfy the
equations
a
kj
a
jk
; 3:16
that is,
~
A and its transpose are equal
~
A
~
A
T
. For example,
~
A
157
53ÿ4
7 ÿ40
0
B
@
1
C
A
is a third-order symmetric matrix: the elements of the ith row equal the elements
of ith column, for all i.
On the other hand, if the elements of
~
A satisfy the equations
a
kj
ÿa
jk
; 3:17
then
~
A is said to be skew-symmetric, or antisymmetric. Thus, for a skew-sym-
metric
~
A, its transpose equ als minus ÿ
~
A:
~
A
T
ÿ
~
A.
Since the elements a
jj
along the principal diagonal sati sfy the equations
a
jj
ÿa
jj
, it is evident that they must all vanish. For example,
~
A
0 ÿ25
201
ÿ5 ÿ10
0
B
@
1
C
A
is a skew-symmetric matrix.
Any real square matrix
~
A may be expressed as the sum of a symmetric matrix
~
R
and a skew-symmetric matrix
~
S, where
~
R
1
2
~
A
~
A
T
and
~
S
1
2
~
A ÿ
~
A
T
: 3:18
Example 3.7
The matrix
~
A
23
5 ÿ1
may be written in the form
~
A
~
R
~
S, where
~
R
1
2
~
A
~
A
T
24
4 ÿ1
~
S
1
2
~
A ÿ
~
A
T
0 ÿ1
10
:
109
SYMMETRIC AND SKEW-SYMMETRIC MATRICES

The product of two symmetric matrices need not be symmetric. This is
because of (3.15): even if
~
A
~
A
T
and
~
B
~
B
T
,
~
A
~
B
T
6
~
A
~
B unless the matrices
commute.
A square matrix whose elements above or below the principal diagonal are all
zero is called a triangular matrix. The following two matrices are triangu lar
matrices:
100
230
502
0
B
@
1
C
A
;
16ÿ1
02 3
00 4
0
B
@
1
C
A
:
A sq uare matrix
~
A is said to be singular if det
~
A 0, and non-singular if
det
~
A 6 0, where det
~
A is the determinant of the matrix
~
A.
The matrix representation of a vector product
The scalar product de®ned in ordinary vector theory has its counterpart in matrix
theory. Consider two vectors A A
1
; A
2
; A
3
and B B
1
; B
2
; B
3
the counter-
part of the scalar product is given by
~
A
~
B
T
A
1
A
2
A
3
B
1
B
2
B
3
0
B
@
1
C
A
A
1
B
1
A
2
B
2
A
3
B
3
:
Note that
~
B
~
A
T
is the transpose of
~
A
~
B
T
,and,beinga1 1 matrix, the transpose
equals itself. Thus a scalar product may be written in these two equivalent forms.
Similarly, the vector product used in ordinary vector theory must be replaced
by something more in keeping with the de®nition of matrix multiplication . Note
that the vector product
A B A
2
B
3
ÿ A
3
B
2
^
e
1
A
3
B
1
ÿ A
1
B
3
^
e
2
A
1
B
2
ÿ A
2
B
1
^
e
3
can be represented by the column matrix
A
2
B
3
ÿ A
3
B
2
A
3
B
1
ÿ A
1
B
3
A
1
B
2
ÿ A
2
B
1
0
B
@
1
C
A
:
This can be split into the product of two matr ices
A
2
B
3
ÿ A
3
B
2
A
3
B
1
ÿ A
1
B
3
A
1
B
2
ÿ A
2
B
1
0
B
@
1
C
A
0 ÿA
2
A
2
A
3
0 ÿA
1
ÿA
2
A
1
0
0
B
@
1
C
A
B
1
B
2
B
3
0
B
@
1
C
A
110
MATRIX ALGEBRA

or
A
2
B
3
ÿ A
3
B
2
A
3
B
1
ÿ A
1
B
3
A
1
B
2
ÿ A
2
B
1
0
B
@
1
C
A
0 ÿB
2
B
2
B
3
0 ÿB
1
ÿB
2
B
1
0
0
B
@
1
C
A
A
1
A
2
A
3
0
B
@
1
C
A
:
Thus the vector product may be represented as the product of a skew-symmetric
matrix and a column matrix. However, this de®nition only holds for 3 3
matrices.
Similarly, curl A may be represented in terms of a skew-symmetric matrix
operator, given in Cartesian coordinates by
rA
0 ÿ @=@x
3
@=@x
2
@=@x
3
0 ÿ@=@x
1
ÿ@=@x
2
@=@x
1
0
0
B
@
1
C
A
A
1
A
2
A
3
0
B
@
1
C
A
:
In a similar way, we can investigate the triple scalar product and the triple vector
product.
The inverse of a matrix
If for a given square matrix
~
A there exists a matrix
~
B such that
~
A
~
B
~
B
~
A
~
I,
where
~
I is a unit matrix, then
~
B is called an inverse of matrix
~
A.
Example 3.8
The matrix
~
B
35
12
is an inverse of
~
A
2 ÿ5
ÿ13
;
since
~
A
~
B
2 ÿ5
ÿ13
35
12
10
01
~
I
and
~
B
~
A
35
12
2 ÿ5
ÿ13
10
01
~
I:
An invertible matrix has a unique inverse. That is, if
~
B and
~
C are both inverses
of the matrix
~
A, then
~
B
~
C. The proof is simple. Since
~
B is an inverse of
~
A,
111
THE INVERSE OF A MATRIX

~
B
~
A
~
I. Multiplying both sides on the right by
~
C gives
~
B
~
A
~
C
~
I
~
C
~
C. On the
other hand, (
~
B
~
A
~
C
~
B
~
A
~
C
~
B
~
I
~
B, so that
~
B
~
C. As a consequence of this
result, we can now speak of the inverse of an invertible matrix. If
~
A is invertible,
then its inverse will be denoted by
~
A
ÿ1
. Thus
~
A
~
A
ÿ1
~
A
ÿ1
~
A
~
I: 3 :19
It is obvious that the inverse of the inverse is the given matrix, that is,
~
A
ÿ1
ÿ1
~
A: 3:20
It is easy to prove that the inverse of the product is the product of the inverse in
reverse ord er, that is,
~
A
~
B
ÿ1
~
B
ÿ1
~
A
ÿ1
: 3:21
To prove (3.21), we start with
~
A
~
A
ÿ1
~
I, with
~
A replaced by
~
A
~
B, that is,
~
A
~
B
~
A
~
B
ÿ1
~
I:
By premultiplying this by
~
A
ÿ1
we get
~
B
~
A
~
B
ÿ1
~
A
ÿ1
:
If we premultiply this by
~
B
ÿ1
, the result follows.
A method for ®nding
~
A
ÿ1
The positive power for a square matrix
~
A is de®ned as
~
A
n
~
A
~
A
~
A (n factors)
and
~
A
0
~
I, where n is a positive integer. If, in addition,
~
A is invertible, we de®ne
~
A
ÿn
~
A
ÿ1
n
~
A
ÿ1
~
A
ÿ1
~
A
ÿ1
n factors:
We are now in position to construct the inverse of an invertible matrix
~
A:
~
A
a
11
a
12
... a
1n
a
21
a
22
... a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
... a
nn
0
B
B
B
B
@
1
C
C
C
C
A
:
The a
jk
are known. Now let
~
A
ÿ1
a
0
11
a
0
12
... a
0
1n
a
0
21
a
0
22
... a
0
2n
.
.
.
.
.
.
.
.
.
a
0
n1
a
0
n2
... a
0
nn
0
B
B
B
B
@
1
C
C
C
C
A
:
112
MATRIX ALGEBRA

The a
0
jk
are required to construct
~
A
ÿ1
. Since
~
A
~
A
ÿ1
~
I, we have
a
11
a
0
11
a
12
a
0
12
a
1n
a
0
1n
1;
a
21
a
0
21
a
22
a
0
22
a
2n
a
0
2n
0;
.
.
.
a
n1
a
0
n1
a
n2
a
0
n2
a
nn
a
0
nn
0:
3:22
The solut ion to the above set of linear algebr aic equations (3.22) may be facili-
tated by applying Cramer's rule. Thus
a
0
jk
cofactor a
kj
det
~
A
: 3:23
From (3.23) it is clear that
~
A
ÿ1
exists if and only if matrix
~
A is non-singular (that
is, det
~
A 6 0).
Systems of linear equations and the inverse of a matrix
As an immediate application, let us apply the concept of an inverse matrix to a
system of n linear equations in n unknowns x
1
; ...; x
n
:
a
11
x
1
a
12
x
2
a
1n
x
n
b
1
;
a
21
x
2
a
22
x
2
a
2n
x
n
b
2
;
.
.
.
a
n1
x
n
a
n2
x
n
a
nn
x
n
b
n
;
in matrix form we have
~
A
~
X
~
B; 3:24
where
~
A
a
11
a
12
... a
1n
a
21
a
22
... a
2n
.
.
.
.
.
.
.
.
.
a
n1
a
n2
... a
nn
0
B
B
B
B
@
1
C
C
C
C
A
;
~
X
x
1
x
2
.
.
.
x
n
0
B
B
B
B
@
1
C
C
C
C
A
;
~
B
b
1
b
2
.
.
.
b
n
0
B
B
B
B
@
1
C
C
C
C
A
:
We can prove that the above linear system possesses a unique solution given by
~
X
~
A
ÿ1
~
B: 3:25
The proof is simple. If
~
A is non-singular it has a unique inverse
~
A
ÿ1
. Now pre-
multiplying (3.24) by
~
A
ÿ1
we obtain
~
A
ÿ1
~
A
~
X
~
A
ÿ1
~
B;
113
SYSTEMS OF LINEAR EQUATIONS

but
~
A
ÿ1
~
A
~
X
~
A
ÿ1
~
A
~
X
~
X
so that
~
X
~
A
ÿ1
~
B is a solution to 3:24;
~
A
~
X
~
B:
Complex conjugate of a matrix
If
~
A a
jk
is an arbitrary matrix whose elements may be complex numbers, the
complex conjugate matrix, denoted by
~
A*, is also a matrix of the same order,
every element of which is the complex conjugate of the co rresponding element of
~
A, that is,
A*
jk
a
*
jk
: 3:26
Hermitian conjugation
If
~
A a
jk
is an arbitrary matrix whose elements may be complex numbers, when
the two operations of transpo sition and complex conjugation are carried out on
~
A, the resulting matrix is called the hermitian conjugate (or hermitian adjoint) of
the original matrix
~
A and will be denoted by
~
A
y
. We frequently call
~
A
y
A-dagger.
The order of the two operations is immaterial:
~
A
y
~
A
T
*
~
A*
T
: 3:27
In terms of the elements, we have
~
A
y
jk
a
*
kj
: 3 :27a
It is clear that if
~
A is a matrix of order m n, then
~
A
y
is a matrix of order n m.
We can prove that, as in the case of the transpose of a product, the adjoint of the
product is the product of the adjoints in reverse:
~
A
~
B
y
~
B
y
~
A
y
: 3:28
Hermitian/anti-hermitian matrix
A matrix
~
A that obeys
~
A
y
~
A 3:29
is called a hermitian matr ix. It is very clear the following matrices are hermitian:
1 ÿi
i 2
;
45 2i 6 3i
5 ÿ 2i 5 ÿ1 ÿ 2i
6 ÿ 3i ÿ1 2i 6
0
B
@
1
C
A
; where i
ÿ1
p
:
114
MATRIX ALGEBRA
Evidently all the elements along the principal diagonal of a hermitian matrix must
be real.
A hermitian matrix is also de®n ed as a matrix whose transpose equals its
complex conjugate:
~
A
T
~
A* that is; a
kj
a
*
jk
: 3:29a
These two de®nitions are the same. First note that the elements in the principal
diagonal of a hermitian matrix are always real. Furthermore, any real symmetric
matrix is hermitian, so a real hermitian matrix is a symmetric matrix.
The pro duct of two hermitian matrices is not generally hermi tian unless they
commute. This is because of property (3.28): even if
~
A
y
~
A and
~
B
y
~
B,
~
A
~
B
y
6
~
A
~
B unless the matr ices commute.
A matrix
~
A that obeys
~
A
y
ÿ
~
A 3:30
is called an anti-hermitian (or skew-hermitian) matrix. All the elements along the
principal diagonal must be pure imaginary. An example is
6i 5 2i 6 3i
ÿ5 2i ÿ8i ÿ1 ÿ 2i
ÿ6 3i 1 ÿ 2i 0
0
B
@
1
C
A
:
We summarize the three operations on matrices discussed above in Table 3.1.
Orthogonal matrix (real)
A matrix
~
A a
jk
mn
satisfying the relations
~
A
~
A
T
~
I
n
; 3:31a
~
A
T
~
A
~
I
m
3:31b
is called an orthogonal matrix. It can be shown that if
~
A is a ®nite matrix satisfy-
ing both relations (3.31a) and (3.31b), then
~
A must be square, and we have
~
A
~
A
T
~
A
T
~
A
~
I: 3:32
115
ORTHOGONAL MATRIX (REAL)
Table 3.1. Operations on matrices
Operation Matrix element
~
A
~
B If
~
B
~
A
Transposition
~
B
~
A
T
b
ij
a
ji
m nn m Symmetric
a
Complex conjugation
~
B
~
A* b
ij
a*
ij
m nm n Real
Hermitian conjugation
~
B
~
A
T
* b
ij
a*
ji
m nn m Hermitian
a
For square matrices only.
