Crank J. Free and Moving Boundary Problems
Подождите немного. Документ загружается.


362
Numerical solution
of
free-boundary problems
TABLE
8.7
Comparison
of
boundary ordinates
x
0.50000
0.5333
0.5667
0.6000
0.6333
0.6667
(a)
0.7333
0.7000
0.6667
0.6304
0.5876
0.5302
(b)
0.7250
0.7000
0.6667
0.6300
0.5868
0.5289
(c)
0.7282
0.6980
0.6651
0.6286
0.5866
0.5300
(a),
(b)
minimization method with mesh sizes
1/60, 1/20 respectively (Aitchison 1977).
(c)
trial free-boundary iterative method with
mesh size 1/60 (Aitchison 1972).
Aitchison (1977) quoted preliminary numerical values of free-boundary
ordinates before smoothing and illustrated
the
stepwise nature of the
whole boundary. Then a least-squares straight line was fitted through
points
Yi>
where Y
==
Y -
(xhr
)In(
-x).
Table 8.6 shows the effect of the
number of points included in the fitting on
Yn
the ordinate of the
separation point.
The
best straight line
is
also used
to
improve internal
free-boundary ordinate values within the range of the fitting.
Table
8.7
compares boundary ordinates for
0.5000:0;;;;
x
:0;;;;0.6667
ob-
tained by Aitchison's minimization method
(1977) and
her
iterative
method
(1972) coupled with the singular solution in each case.
The
earlier computations were revised and extended
to
include a smaller grid
size.
Tables
8.8-17,19,20
contain numerical results extracted from tables
TABLE
8.8
Ordinates fz(x)
of
the sea-
water boundary for a coastal
aquifer (§2.5). Length
of
aquifer = a = 1000; height
of
aqUifer above sea level =
Yl
=
2, P =
(Pc
P.)/Pt.
=
-0.03,
fZ{O)
= Yl/P =
-66.66.
Mesh
points
80
x 60
x
-fix)
x
-fix)
0 66.66
700 36.91
100
63.23
750 33.47
200
59.80 800
30.04
300 56.36 850
25.46
400 51.78
900
20.88
500 47.21
950 15.16
600
42.63 987
8.30

Variational inequality and complementarity methods
363
TABLE
8.9
TABLE
8.10
Ordinates
of
free boundary for
Ordinates
of
free boundary
vertically stratified dam:
Yl
=
for
vertically stratified dam:
1.33,
Y2=0.
Permeability
Yl
= 1.33,
Y2
=
O.
Permea-
coefficients
k'=0.197
in
0".;;
bility coefficients
k'
= 1.46
x<l,
k"=
1.46
in
1<x".;;2
in O".;;x<l,
k"=0.197
in
(§2.8.1); mesh points
60x
100
1<x".;;2 (§2.8.1);
mesh
in each
half
points 20 x 40 in each
half
x
y
x
y x
y
x
y
0.00 1.330
1.00
0.611 0 1.333 1.0 1.230
0.10 1.263
1.10 0.452
0.1 1.296
1.1
1.197
0.20
1.230
1.20 0.412 0.2 1.296 1.2
1.163
0.30
1.197
1.30 0.385 0.3 1.263 1.3
1.130
0.40 1.130
1.40 0.332 0.4 1.263
1.4
1.064
0.50
1.097
1.50
0.299 0.5 1.263 1.5 0.997
0.60
1.030 1.60
0.268 0.6 1.263 1.6 0.931
0.70 0.984
1.70 0.232
0.7
1.263 1.7 0.864
0.80 0.904
1.80 0.199 0.8 1.230 1.8
0.764
0.90
0.811
1.90 0.133 0.9 1.230 1.9
0.665
1.00
0.611
1.95 0.099 1.0
1.230
1.95 0.598
TABLE
8.11
TABLE
8.12
Ordinates
of
free boundary for Ordinates
of
free boundary for
hOrizontally stratified dam:
Yl
= horizontally stratified dam:
Yl
=
0.721,
Y2
= 0.253 95,
a = 1.0.
0.814,
Y2
= 0.128 88, a = 1.0.
Permeability
coefficients
k'=
Permeability coefficients
k'=
0.0296
in O".;;y<0.496,
k"=
0.737 in
O".;;y
<0.323,
k"=
0.737 in
0.496<y"';;0.721
0.0296
in 0.323 < Y
:E;;0.814
(§2.8.1); Mesh points 40 x 20 in (§2.8.1); mesh points 4Ox20 in
each part lower part;
40 x 40
in
upper part
x
y
x
y
x
y
x
y
0
0.721 0.55
0.631 0.00
0.814
0.55
0.531
0.050
0.709
0.60
0.619
0.05
0.789 0.60 0.494
0.10
0.698
0.65 0.608 0.10
0.777
0.65
0.458
0.15 0.687 0.70 0.597 0.15
0.752
0.70 0.421
0.20
0.687
0.75 0.586 0.20
0.728 0.75 0.372
0.25
0.676
0.80 0.574 0.25
0.703 0.80 0.323
0.30
0.664
0.85 0.563 0.30 0.678
0.85
0.290
0.35 0.664 0.90 0.541 0.35
0.654 0.90 0.274
0.40 0.653 0.95 0.529 0.40
0.629 0.95
0.226
0.45 0.642
0.975 0.518
0.45 0.593
0.975 0.209
0.50 0.631
0.50
0.568

364
Numerical solution
of
free-boundary problems
presented by Baiocchi et
al.
(1973a) and obtained by using
the
Cryer
algorithm (8.90).
(ii) Three dimensional. Caffrey and Bruch (1979) extended
the
finite-
difference version
of
the
Cryer algorithm (8.90) to three dimensions using
7-point formulae for the Laplacian operator. Denoting by
wi,i.k
the
value
of
w(x,
y,
z)
at
the
grid point
(i
llx,
illy,
k llz) the
SOR
scheme with
projection becomes
W~'!+~)
=.!.
{_1_
[w~n)
. +
w~n+~),J+_1_
[W~,!+I)
+
w~'!)
]
•.
I.k
2ll
llx
2
.-I.I,k
.+1.1.
lly2 ',I-l.k
',I+l,k
+
~[
(n) +
(n+l)
]-1}
llz2
Wi,i,k-l
Wi.i.k+1
,
W~'!+
1)
=
max[O
W~'!)
+
W(W~'!+~)
-
W~'!)
\]
•.
I.k
,
•.
I,k
'.I,k
',I.1cJ
,
where
II
= l/llX2+
l/lly2+
1/llz2.
(8.92)
The
finite-element discretization can be applied to
the
minimum for-
mulation
of
the
variational inequality (2.86) for example.
It
is
required
to
find w such that
J(
w)
..;
J(
v)
for all v where
J(v)=~
J J
J{
(!:r
+
G;r
+
(!:r
+v}
dx dy dz.
D
(8.93)
In
an element of
the
mesh, w
is
defined as usual by
w = w(x,
y,
z)
= [N]{w}e=[N;,
Nj,
...
,
Np]{w}e
(8.94)
where
N;,
Nj,
,
..
,
Np
are piecewise linear shape functions, which can
be
expressed in terms
of
the
nodal values
of
w.
Insertion of the approxima-
tion (8.94) for v and minimizing gives typically
JJJ(
oN
1
aw
aN10w
aN1oW)
)
--+--+--
+N
1
dxdydz=O.
ax
oX
oy oy
oZ
oZ
D
(8.95)
A typical finite-element used by Caffrey and Bruch (1979) in
the
form
of
a rectangular prism is shown in Fig. 8.14.
It
includes
26
neighbouring
nodes
to
approximate w at any node.
For
convenience
the
following
nomenclature
is
introduced:
a=2/llx,
b=2/lly,
c=2/llz,
18abc=1/V,
El
=-(a
2
+b
2
+c
2
)V, E
8
=-32E
l
;
E2 =
(-4a
2
-4b
2
+2c
2
)V,
E3 =
(-4a
2
+ 2b
2
-4c
2
) V,
E4 = (2a
2
-4b
2
-
4c
2
)
V;
Es
=
(-16a
2
+ 8b
2
+ 8c
2
)
V,
E6=(8a
2
-16b
2
+8c
2
)V,
E7= (8a
2
+8b
2
-16c
2
)V.

Variational inequality and complementarity methods
365
W8~
______
W~~~
______
~.
x
FIG. 8.14. Three-dimensional finite element molecule
In
Fig.
8.14
we identify
Wi,i,k
=
WI.
Wi-l,i,k
=
W2,
Wi-l,i-l,k-l =
Wg,
etc. so
that
the
SOR
with projection can
be
written
wln+~
= - Eg{El[
w~n)
+
w~n)
+
wl'({
+
wl'i.+
1
) +
wl~
+
w\'3+
1
) + wl'2
+wl'S+1)]
+ Ez[
wlr:{
+
w~'7+1)
+
wl~+1)
+ wl'¥]
+ E
3
[
w&'({
+
w&'i.+
1
) +
w~
+
w&'3+
1
)]
+ E
4
[
w&'2
+
w&'S+1)
+
wg:;
+
W&'7+
1
)]+
Es[
w&n)
-
w~n+l)]
+
E6[W~n)
+
w~n+l)]+
E7[W~n)
+
w~n+l)]+
8/(abc)},
w('!+l)=max[O
w('!)
+w(w('!+!)-w('!»)]
1,I,k
'",I,k
1,I,k
1,I,k'
(8.96)
With regard
to
the
boundary conditions, since
the
w-values
on.
the
impervious
bottom
of
the
dams considered by Caffrey and Bruch (1979)
are
known
to
satisfy Laplace's equation,
the
bottom boundary
is
approxi-
mated by an appropriate two-dimensional finite-difference
or
finite-
element discretization.
The
values
of
w along
the
intersections
of
the
bottom and
the
inlet and exit faces
are
known Dirichlet data,
but
along
the
intersections with
the
impervious sides a zero normal derivative exists.
The
fictitious .points outside
the
region
are
eliminated in
the
usual way,
i.e. they
are
equated
to
the
corresponding node just inside
the
boundary.
The
w-values
allover
the
dam
bottom
are
then used as Dirichlet data for

366
Numerical solution
of
free-boundary problems
x
FIG. 8.15.
Free
surface location for first dam configuration
the internal computations throughout the dam. These start at one imper-
vious side, with similar treatment of all fictitious nodes; and similarly on
the opposite side at the end of the computation.
The
free surface computed in the first dam studied by Caffrey and
Bruch (1979)
is
shown in Fig. 8.15.
The
details of the dam are shown in
Fig. 8.16a. Calculations by finite differences and finite elements showed
only minor differences. A mesh size of
ax
=
ay
=
az
= 1 m gave a total of
2541 nodes and
to
satisfy a convergence criterion
max
IW~,!+l)_W~'!)
\<0.001
1,1,k
1,1,k
,
ijk
45 iterations and a computer time of 7.74 seconds were needed with finite
differences compared with 46 iterations in 15.62 seconds using finite
elements; in both cases compilation and linkage editing time were ex-
cluded. In both cases the relaxation factor
w was 1.75. Convergence and
accuracy were examined numerically.
The second dam (Fig. 8.16b) was studied only by finite differences
with grid spacings
ax
= 20
m,
ay
= 3 m,
az
= 60 m, and 15 708 nodes.
To
satisfy a convergence criterion of 1.00 required 131 iterations in 83.99
seconds with a relaxation factor of 1.75 again. Caffrey and Bruch (1979)
made comparisons with results for a similar but not identical dam
obtained by France (1974) using finite elements.

T
20m
T
10m
____
1
Top
view
j--1Om-l
'il
Side
view
lOin
1
'il
:2m
.
......
1.
---2Om---I,1
FIG. 8.16(a}. Three-dimensional dam, first numerical example
It--o
--
440m
'I
Top
view
600m
FIG. 8. 16(b). Three-dimensional dam, second numerical example

368
Numerical solution
of
free-boundary problems
(iii) Compatability condition. In some free-boundary problems
the
boundary conditions contain an unknown parameter which has to
be
determined as
part
ot' the process of solution such that some additional
criterion
is
satisfied.
An
example is
the
problem of
the
rectangular
dam
with a sheetpile
on
the
inlet face (see §2.3.2).
Here
the flow rate q
is
not
known a
priori,
but
is
to
be
determined so that
the
condition (2.57) is
satisfied by
the
solution.
An
outer iteration
on
q
to
find
the
root of (2.57)
can
be
based
on
the
secant method so that
(r)
(r-1)
(r+1)
-
(r)
q - q
I'
(
(r))
(8 97)
q
-q
!h(q(r))-fh(q(r-1))
Jh
q . .
Baiocchi et
al.
(1973a) and Bruch (1980) described a method
of
combin-
ing (8.97) with
the
complementarity projection algorithms (8.90)
or
(8.91).
An
initial guess for W q'Ol.iJ
is
made, usually zero, together with a guess
at
q =
q(O).
In
fact, two initial guesses,
q(O)
and
q(l),
will
be
needed.
Successive steps
are
as follows:
(i) Solve (8.90)
or
(8.91) using
q(O)
and starting
the
innt<r
iteration
with
W~9~'.i.i
to
obtain successively
w~~~>'i,i>
W~~~).iJ'
etc.
till
some
prescribed convergence criterion
is
satisfied. Then
fh(q(O))
is
evaluated from (2.57) by using W
q
'O).1.G and wq'O).o.G and its con-
vergence criterion examined. As in
the
derivation of (2.57), these
are values of W
at
x =
~x
and x = 0
on
the
horizontal mesh line
through G in Fig. 2.3 obtained with estimate
g(O).
(ii) Using Wq(Ol,iJ as
the
initial guess for
W~%.iJ
solve (8.90)
or
(8.91)
again but using
the
second guessed value
q(1)
which
is
to
be
larger
than
q(O).
The
solution Wq(l).i.i is used now
to
evaluate
fh(q(1))
from
(2.57) and insertion of
q(O),
q(1),
fh(q(O))
and
fh(q(1))
into (8.97)
yields a further estimate,
q(2).
(iii)
The
scheme
is
repeated starting with
q(2)
and W
q'".i.i
to
obtain
Wq(Z).iJ and fh(q(2)) and so
on
till
the
convergence criteria for both
inner and outer iterations are satisfied.
Baiocchi et al. (1973a) used this double-iterative scheme with
the
finite-difference algorithm (8.90)
to
obtain the'boundary ordinates for a
dam with a sheetpile having
the
specifications set
out
in Table 8.13.
The
iteration details are given in Table 8.14. Similar information
is
presented
by Baiocchi et
al.
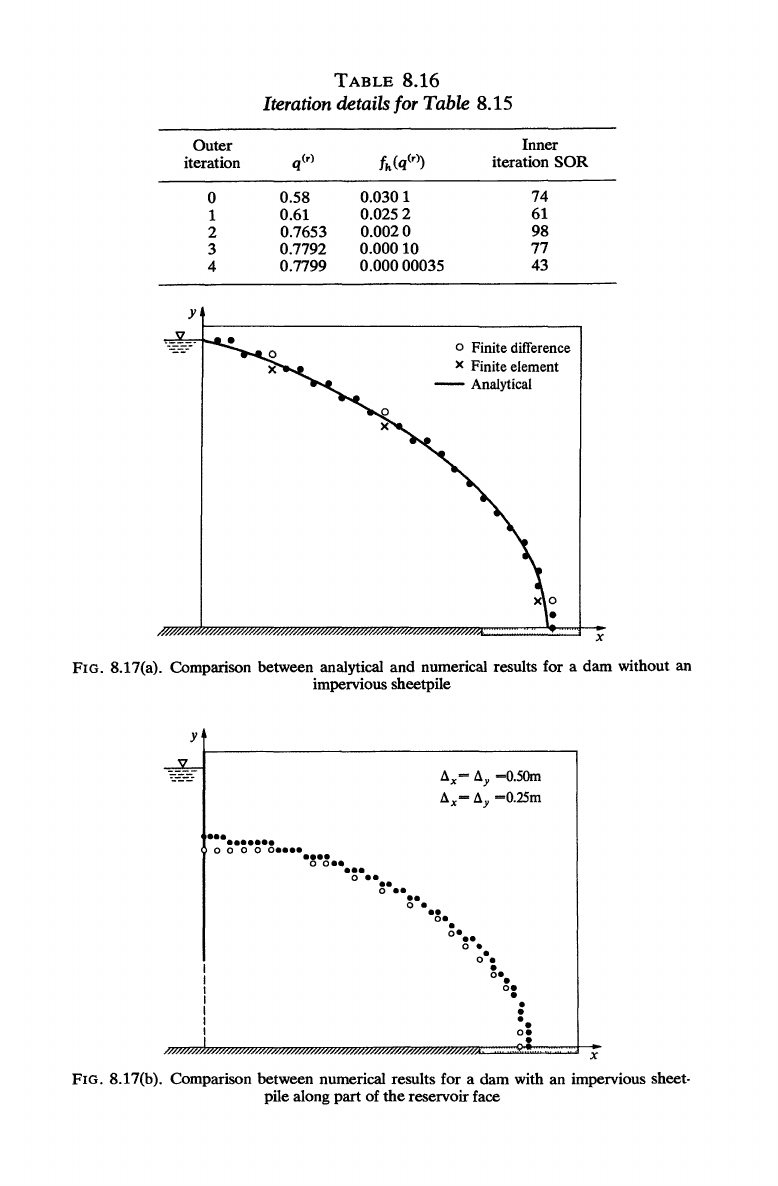
(1973a) for two different dams. Tables 8.15 and 8.16
give extracted results for
the
case
of
relatively smallest sheetpile. Solu-
tions for both dams were also obtained by a trial free-boundary method
which took a longer computing time
to
achieve
the
same accuracy.
Bruch and Caffrey (1979) used
the
compatability condition and an
SOR
iteration
to
obtain both finite-difference and finite-element solutions

TABLE
8.13
Ordinates
of
the
free
sur-
face
for
a dam with a
sheetpile on the inlet face:
Yl
= 4,
Yz
= 1.5, a = 10, c =
0.1 (§2.3.2); mesh points
x
0.0
0.5
1.0
1.5
2.0
2.5
3.0
3.5
4.0
4.5
5.0
60x60
y
2.666
2.666
2.600
2.600
2.533
2.533
2.466
2.400
2.333
2.266
2.200
x
5.0
5.5
6.0
6.5
7.0
7.5
8.0
8.5
9.0
9.5
9.833
y
2.200
2.133
2.066
2.000
1.933
1.866
1.800
1.733
1.666
1.533
1.466
TABLE
8.14
Iteration details
for
Table 8.13
Outer iteration
qt
r
)
Mq(r»
Inner iteration SOR
0 0.025 0.13443 68
1
0.0384 0.12677
51
2 0.2597 0.01501 89
3
0.2894
0.00124
88
4
0.2921"
0.000009
62
"The
authors quote 1 per cent agreement with earlier values
obtained by Maione and Franzeiti (1969)
using
experimental and
approximate analytic methods.
TABLE
8.15
Ordinates
of
the
free
surface
for
a
dam with a sheetpile on the inlet
face:
Yl
= 1.5,
Yz
= 0.3, a = 1, c =
05
(§2.3.2); mesh points
40x60
x
y
x
y
0.00 1.050 0.50
0.950
0.05 1.050 0.55 0.925
0.10
1.050 0.60 0.900
0.15 1.025
0.65
0.875
0.20 1.025 0.70 0.850
0.25 1.025
0.75
0.825
0.30 1.000
0.80
0.775
0.35 1.000
0.85
0.725
0.40
0.975 0.90 0.700
0.45
0.975 0.95 0.625
0.50
0.950 0.975 0.600
TABLE
8.16
Iteration
details
for
Table 8.15
Inner
Outer
iteration
q(rl
Mq(rl)
iteration
SOR
y
o
1
2
3
4
0.58
0.61
0.7653
0.7792
0.7799
0.0301
74
0.0252
61
0.0020
98
0.00010
77
0.00000035 43
~------------------------------~
=~-'-L'·
--
o Finite
difference
x Finite element
--
Analytical
o
•
x
FIG.
8.17(a). Comparison between analytical and numerical results for a dam without an
impervious sheetpile
y
...
.......
o 0 0 0 0
••••
....
00
••
...
o
••
..
o
••
..
I1x=
l1y
-O.5Om
I1x-l1y
-O.25m
o •
..
o •
.
0
•••
o •
.
o.
o
o.
o
00
o
.
o
·0
00
x
FIG.
8.17(b). Comparison between numerical results for a dam with an impervious sheet·
pile along part of
the
reservoir face

Variational inequality and complementarity methods
371
TABLE
8.17
Ordinates
of
the
free
surface
for
a dam
with sloping inlet face (§2.3.4):
Yl
= 1,
Y2
= 0,
al
= 1, a = 3; square mesh size
0.05
X
ya y*a
X
y
y*
0.0
1.00 1.00
1.0 0.65
0.67
0.1
0.95 0.95
1.1 0.60
0.64
0.2
0.90
0.92 1.2 0.60
0.60
0.3
0.85
0.88 1.3
0.55 0.57
0.4
0.85
0.85 1.4 0.50
0.53
0.5
0.80
0.82 1.5 0.45
0.48
0.6
0.80
0.80 1.6
0.40
0.43
0.7
0.75
0.77
1.7
0.35
0.38
0.8
0.70 0.74
1.8 0.30
0.32
0.9
0.70
0.70 1.9 0.25
0.23
1.0 0.65
0.67 1.95
0.20 0.17
a
y*
computed by a trial free-boundary method;
y by complementarity with compatibility itera-
tion.
for a dam with a sheetpile and a toe drain (see §2.3.3). Where there is a
toe
drain
but
no sheetpile
the
compatability condition is not required and
there is an analytical solution (Harr, 1962,
p.
223).
In
Fig. 8.17a Bruch
and Caffrey compared their three solutions for
the toe
drain without a
sheetpile and Fig. 8.17b shows
the
effect of introducing a sheetpile.
Problems in dams of some other important geometric shapes involve
the
compatability condition.
The
dam with a slanting inlet face (Fig. 2.5)
is such a case solved by Baiocchi et al. (1973a) using a suitably modified
form of the double-iteration cycle and finite differences. An extract of
their results is compared in Table 8.17, with values computed by a trial
free-boundary method.
The
latter do not exhibit
the
stepwise behaviour
TABLE
8.18
Iteration details
for
dam with sloping inlet face and toe
drain (§2.3.5): allYl = 1.0, alYl = 3.16; square mesh
size
tiX/Yl
= tiy/Yl = 0.05
Outer Inner
iteration
q(r)
fh(q(r))
iteration
SOR
0
0.23000
0.01679
77
1
0.25000
0.02898
54
2
0.20247
0.00079
63
3
0.20115
0.00012
24
