Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.

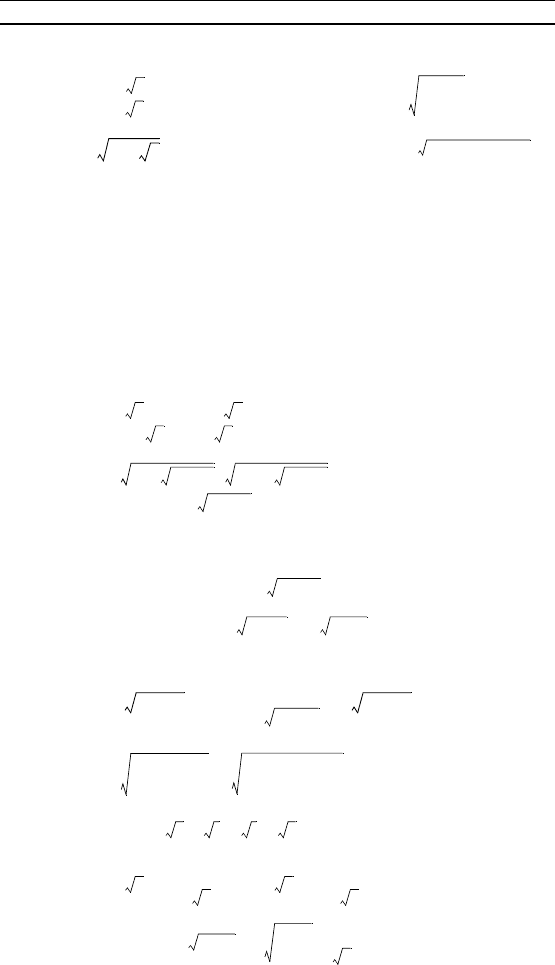
220 Г л а в а 9. Производная и ее применения
Найдите производную сложной фунции:
12. y = . 13. y = .
14. y = . 15. y = .
16. y = arctg . 17. y = .
18. y = cos
3
x (3 cos
2
x – 5). 19. y = ln cos .
20. y = .
Предварительно упростив выражение, найдите производ-
ную фунции:
21. f(x) = .
22. f(x) = .
23. f(x) = .
24. f(x) =
25. f(x) = ( + 1) : + .
26. f(x) = .
27. f(x) = .
2 x+
2 x–
------------------
1 x
2
–
1 x
2
+
---------------- -
sin x e
ln ax
2
bx c++()
1 x+
1 x–
------------- -
abx
n
+()
m
abx
n
–()
m
-----------------------------
1
15
------
x 1–
x
-------------
tg
2
x 1–()tg
4
x 10 tg
2
x 1++()
3tg
3
x
----------------------------------------------------------------------------------------
x 1+()x
2
x–()
xx x x++
-------------------------------------------------
x 2 x
2
–+
3
1 x 2 x
2
––
6
1 x
2
–
3
------------------------------------------------------------------------------ -
1 x
2
–()
1/2–
1
1
1 x
2
–()
1/2–
1–
------------------------------------------
++
2–
2 x
2
–21x
2
––
-------------------------------------------------------------------------------------------------------- -
(x
2/ m
9x
2/ n
)( x
1 m–
n
–3x
1 n–
n
)–
(x
1/m
3x
1/n
)
2
12x
(mn)/(mn)+
–+
------------------------------------------------------------------------------------------------ .
1 x
4
–
1
1 x
2
+
---------------------
1 x
2
–
1
2
---
3–
t
3
–
3
t
5
2t
4
4t
3
++
44t– t
2
+
------------------------------------- -
3
+
1
2 t–
-------------------- -
1
t 2+
---------------------
+
------------------------------------------------------------------------------------ -
x 2+()
2
x
-------
1–
x 2–()
2
x
-------
1+
–
2 x 2+–():
2
x
---
1+
2
x
-------
–
---------------------------------------------------------------------------------------------------------
§ 46. Нахождение производных 221
28. f(x) = .
29. f(x) = .
30. f(x) = .
31. f(x) = + · .
Если фунция f(x) определена на неотором промежуте
[a; b], то в ачестве значений ее производных на онцах этоо
промежута принимают значения левой производной на пра-
вом онце и правой — на левом онце.
Пример4. Найти производную фунции f(x)=
= на промежуте [0; 2].
Р е ш е н и е. Выражение под знаом радиала представля-
ет собой полный вадрат, поэтому, соласно определению мо-
дуля, представим данную фунцию в следующем виде:
f(x) = |x – 1| = (*)
Дифференцируя f(x) по отдельности на промежутах [0; 1) и
(1; 2], получаем
(x) =
Та а левая и правая производные в точе x = 1 не совпада-
ют, то в этой точе производная не существует; в ачестве зна-
чений (x) на онцах промежута [0; 2] принимаем значения
левой производной фунции (*) в точе x = 2 в правой произ-
водной фунции (*) в точе x = 0.
Ответ.(x) =
2x 2 x
2
1–+
3
x 1–
x 1+
------------------
x 1+
x 1–
------------------
2++
1/3
---------------------------------------------------------------------
x 1–
x 1+
--------------
x 1+
x 1–
------------- -
2–+2xx
2
1–+()
(x 1)
3
+(x 1)
3
––
-----------------------------------------------------------------------------------------------------
11x
2
–+1x+()
3
1 x–()
3
–()
21x
2
–+
---------------------------------------------------------------------------------------------------
ax
3
4
a
3
x
4
–
ax–
-------------------------------------
1 ax+
ax
4
----------------------
2–
12
a
x
---
a
x
---
++
x
2
2x–1+
1 – x, x Ý [0; 1),
x – 1, x Ý [1; 2].
f
′
–1, x Ý [0; 1),
–1, x Ý (1; 2].
f
′
f
′
–1, x Ý [0; 1),
–1, x Ý (1; 2].

220 Г л а в а 9. Производная и ее применения
Найдите производную сложной фунции:
12. y = . 13. y = .
14. y = . 15. y = .
16. y = arctg . 17. y = .
18. y = cos
3
x (3 cos
2
x – 5). 19. y = ln cos .
20. y = .
Предварительно упростив выражение, найдите производ-
ную фунции:
21. f(x) = .
22. f(x) = .
23. f(x) = .
24. f(x) =
25. f(x) = ( + 1) : + .
26. f(x) = .
27. f(x) = .
2 x+
2 x–
------------------
1 x
2
–
1 x
2
+
---------------- -
sin x e
ln ax
2
bx c++()
1 x+
1 x–
------------- -
abx
n
+()
m
abx
n
–()
m
-----------------------------
1
15
------
x 1–
x
-------------
tg
2
x 1–()tg
4
x 10 tg
2
x 1++()
3tg
3
x
----------------------------------------------------------------------------------------
x 1+()x
2
x–()
xx x x++
-------------------------------------------------
x 2 x
2
–+
3
1 x 2 x
2
––
6
1 x
2
–
3
------------------------------------------------------------------------------ -
1 x
2
–()
1/2–
1
1
1 x
2
–()
1/2–
1–
------------------------------------------
++
2–
2 x
2
–21x
2
––
-------------------------------------------------------------------------------------------------------- -
(x
2/ m
9x
2/ n
)( x
1 m–
n
–3x
1 n–
n
)–
(x
1/m
3x
1/n
)
2
12x
(mn)/(mn)+
–+
------------------------------------------------------------------------------------------------ .
1 x
4
–
1
1 x
2
+
---------------------
1 x
2
–
1
2
---
3–
t
3
–
3
t
5
2t
4
4t
3
++
44t– t
2
+
------------------------------------- -
3
+
1
2 t–
-------------------- -
1
t 2+
---------------------
+
------------------------------------------------------------------------------------ -
x 2+()
2
x
-------
1–
x 2–()
2
x
-------
1+
–
2 x 2+–():
2
x
---
1+
2
x
-------
–
---------------------------------------------------------------------------------------------------------
§ 46. Нахождение производных 221
28. f(x) = .
29. f(x) = .
30. f(x) = .
31. f(x) = + · .
Если фунция f(x) определена на неотором промежуте
[a; b], то в ачестве значений ее производных на онцах этоо
промежута принимают значения левой производной на пра-
вом онце и правой — на левом онце.
Пример4. Найти производную фунции f(x)=
= на промежуте [0; 2].
Р е ш е н и е. Выражение под знаом радиала представля-
ет собой полный вадрат, поэтому, соласно определению мо-
дуля, представим данную фунцию в следующем виде:
f(x) = |x – 1| = (*)
Дифференцируя f(x) по отдельности на промежутах [0; 1) и
(1; 2], получаем
(x) =
Та а левая и правая производные в точе x = 1 не совпада-
ют, то в этой точе производная не существует; в ачестве зна-
чений (x) на онцах промежута [0; 2] принимаем значения
левой производной фунции (*) в точе x = 2 в правой произ-
водной фунции (*) в точе x = 0.
Ответ.(x) =
2x 2 x
2
1–+
3
x 1–
x 1+
------------------
x 1+
x 1–
------------------
2++
1/3
---------------------------------------------------------------------
x 1–
x 1+
--------------
x 1+
x 1–
------------- -
2–+2xx
2
1–+()
(x 1)
3
+(x 1)
3
––
-----------------------------------------------------------------------------------------------------
11x
2
–+1x+()
3
1 x–()
3
–()
21x
2
–+
---------------------------------------------------------------------------------------------------
ax
3
4
a
3
x
4
–
ax–
-------------------------------------
1 ax+
ax
4
----------------------
2–
12
a
x
---
a
x
---
++
x
2
2x–1+
1 – x, x Ý [0; 1),
x – 1, x Ý [1; 2].
f
′
–1, x Ý [0; 1),
–1, x Ý (1; 2].
f
′
f
′
–1, x Ý [0; 1),
–1, x Ý (1; 2].
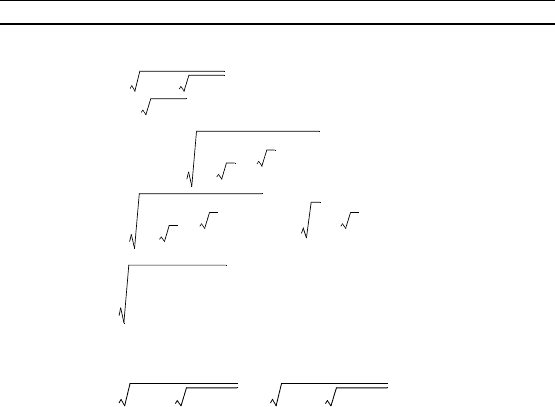
222 Г л а в а 9. Производная и ее применения
Найдите производную фунции:
32. f(x) = x .
33. f(x) = .
34. f(x) = .
35. f(x) = + .
§ 47. Промежутки монотонности
и экстремумы функции
Исследование фнции на монотонность. Говорят, что
фунция y = f(x) возрастает на промежте (a; b), если для
любых x
1
и x
2
, принадлежащих (a; b), из неравенства x
1
< x
2
следует неравенство f(x
1
) < f(x
2
). Говорят, что фунция y = f(x)
бывает на промежте (a; b), если для любых x
1
и x
2
, при-
надлежащих (a; b), из неравенства x
1
< x
2
следует неравенство
f(x
1
) > f(x
2
). Фунции, возрастающие (убывающие) на проме-
жуте (a; b), называют монотонными на этом промежте.
Достаточные словия монотонности фнции. Пусть
фунция y = f(x) определена и дифференцируема на промежут-
е (a; b). Для тоо чтобы фунция была возрастающей на
промежуте (a; b), достаточно, чтобы выполнялось условие
(x) > 0 при любом x Ý (a; b).
Для тоо чтобы фунция была убывающей на промежут-
е (a; b), достаточно, чтобы выполнялось условие (x) < 0
при любом x Ý (a; b).
Точи, принадлежащие промежуту (a; b), в оторых про-
изводная равна нулю или не существует, называют ритиче-
x 2 x 1––
x 1–1–
------------------------------------
2x
1
4
---
1
x
-------
x+
2
1–
2
1
4
---
1
x
-------
x+
2
1–
1
2
---
1
x
---
x–
–
---------------------------------------------------------------------------------------------
1
x
2
1–
2x
----------------
2
+
x
2
1+()
1
x
2
------
---------------------------------------- -
x 22x 4–+ x 22x 4––
f
′
f
′
§ 47. Промежутки монотонности и экстремумы функции 223
сими точами фунции y = f(x). Из определения ритиче-
сой точи следует, что если производная фунции меняет
зна, то это может произойти тольо при переходе через ри-
тичесую точу. Таим образом, промежути убывания и воз-
растания (промежути монотонности) фунции f(x) ораниче-
ны ритичесими точами. Поэтому для нахождения проме-
жутов монотонности фунции необходимо:
1) найти ритичесие точи фунции f(x);
2) определить зна производной (x) внутри промежутов,
ораниченных ритичесими точами.
П р и м е р 1. Исследовать на возрастание и убывание
фунцию f(x) = xe
–3x
.
Р е ш е н и е. Находим производную
(x) = e
–3x
– 3xe
–3x
= e
–3x
(1 – 3x).
Производная (x) существует всюду и обращается в нуль в точ-
е x = . Эта точа делит числовую прямую на два промежута:
–×; и ; +× . Та а фунция e
–3x
вседа положи-
тельна, то зна производной определяется вторым сомножите-
лем. На промежуте –×; выполняется неравенство (x) > 0,
а на промежуте ; +× — неравенство (x) < 0.
Ответ.Фунция f(x) возрастает на промежуте –×;
и убывает на промежуте ; +× .
Исследуйте на возрастание и убывание фунцию:
1. f(x) = . 2. f(x) = .
3. f(x) = x – sin
2
x. 4. f(x) = 2 ln (x – 2) – x
2
+ 4x + 1.
5. f(x) = . 6. f(x) = .
f
′
f
′
f
′
1
3
---
1
3
---
1
3
---
1
3
---
f
′
1
3
---
f
′
1
3
---
1
3
---
x
2
2–
2x 3+
----------------- -
x
ln x
----------
3
2
---
2x 1–
x 1–()
2
---------------------
3 x
2
–
x
----------------

222 Г л а в а 9. Производная и ее применения
Найдите производную фунции:
32. f(x) = x .
33. f(x) = .
34. f(x) = .
35. f(x) = + .
§ 47. Промежутки монотонности
и экстремумы функции
Исследование фнции на монотонность. Говорят, что
фунция y = f(x) возрастает на промежте (a; b), если для
любых x
1
и x
2
, принадлежащих (a; b), из неравенства x
1
< x
2
следует неравенство f(x
1
) < f(x
2
). Говорят, что фунция y = f(x)
бывает на промежте (a; b), если для любых x
1
и x
2
, при-
надлежащих (a; b), из неравенства x
1
< x
2
следует неравенство
f(x
1
) > f(x
2
). Фунции, возрастающие (убывающие) на проме-
жуте (a; b), называют монотонными на этом промежте.
Достаточные словия монотонности фнции. Пусть
фунция y = f(x) определена и дифференцируема на промежут-
е (a; b). Для тоо чтобы фунция была возрастающей на
промежуте (a; b), достаточно, чтобы выполнялось условие
(x) > 0 при любом x Ý (a; b).
Для тоо чтобы фунция была убывающей на промежут-
е (a; b), достаточно, чтобы выполнялось условие (x) < 0
при любом x Ý (a; b).
Точи, принадлежащие промежуту (a; b), в оторых про-
изводная равна нулю или не существует, называют ритиче-
x 2 x 1––
x 1–1–
------------------------------------
2x
1
4
---
1
x
-------
x+
2
1–
2
1
4
---
1
x
-------
x+
2
1–
1
2
---
1
x
---
x–
–
---------------------------------------------------------------------------------------------
1
x
2
1–
2x
----------------
2
+
x
2
1+()
1
x
2
------
---------------------------------------- -
x 22x 4–+ x 22x 4––
f
′
f
′
§ 47. Промежутки монотонности и экстремумы функции 223
сими точами фунции y = f(x). Из определения ритиче-
сой точи следует, что если производная фунции меняет
зна, то это может произойти тольо при переходе через ри-
тичесую точу. Таим образом, промежути убывания и воз-
растания (промежути монотонности) фунции f(x) ораниче-
ны ритичесими точами. Поэтому для нахождения проме-
жутов монотонности фунции необходимо:
1) найти ритичесие точи фунции f(x);
2) определить зна производной (x) внутри промежутов,
ораниченных ритичесими точами.
П р и м е р 1. Исследовать на возрастание и убывание
фунцию f(x) = xe
–3x
.
Р е ш е н и е. Находим производную
(x) = e
–3x
– 3xe
–3x
= e
–3x
(1 – 3x).
Производная (x) существует всюду и обращается в нуль в точ-
е x = . Эта точа делит числовую прямую на два промежута:
–×; и ; +× . Та а фунция e
–3x
вседа положи-
тельна, то зна производной определяется вторым сомножите-
лем. На промежуте –×; выполняется неравенство (x) > 0,
а на промежуте ; +× — неравенство (x) < 0.
Ответ.Фунция f(x) возрастает на промежуте –×;
и убывает на промежуте ; +× .
Исследуйте на возрастание и убывание фунцию:
1. f(x) = . 2. f(x) = .
3. f(x) = x – sin
2
x. 4. f(x) = 2 ln (x – 2) – x
2
+ 4x + 1.
5. f(x) = . 6. f(x) = .
f
′
f
′
f
′
1
3
---
1
3
---
1
3
---
1
3
---
f
′
1
3
---
f
′
1
3
---
1
3
---
x
2
2–
2x 3+
----------------- -
x
ln x
----------
3
2
---
2x 1–
x 1–()
2
---------------------
3 x
2
–
x
----------------

224 Г л а в а 9. Производная и ее применения
7. Найдите множество всех значений параметра a, при ото-
рых фунция
f(x) = sin 2x – 8(a – 1) sin x + (4a
2
+ 8a – 14)x
является возрастающей и не имеет ритичесих точе для всех
x Ý R.
8. Найдите всех значения параметра a, при оторых фунция
y(x) = 8ax – a sin 6x – 7x – sin 5x
возрастает и не имеет ритичесих точе для всех x Ý R.
Исследование фнции на эстремм. Говорят, что фун-
ция y = f(x) имеет в точе x
0
масимм (или минимм), если
найдется таая δ-орестность точи x
0
, принадлежащая облас-
ти определения фунции, что для всех x − x
0
, принадлежащих
промежуту (x
0
– δ; x
0
+ δ), выполняется неравенство f(x) < f(x
0
)
(соответственно f(x) > f(x
0
)).
Точи масимума и минимума называют точами эстре-
мма, а значения фунции в этих точах — эстремальными
значениями.
Необходимое словие сществования эстремма фн-
ции. Пусть фунция f(x) дифференцируема на промежуте
(a; b). Тода если в неоторой точе x
0
Ý (a; b) фунция f(x)
достиает эстремума, то (x
0
) = 0.
Достаточное словие сществования эстремма фн-
ции. Пусть фунция определена и непрерывна на промежут-
е (a; b) и на всем промежуте (за ислючением, быть мо-
жет, онечноо числа точе) дифференцируема. Тода если при
переходе через ритичесую точу производная фунции ме-
няет зна, то таая ритичесая точа является точой
эстремума фунции: точой масимума, если зна меняет-
ся с плюса на минус, и точой минимума, если зна меняется
с минуса на плюс.
П р и м е р 2. Найти эстремум фунции
f(x) = .
Р е ш е н и е. Находим производную
(x) = . (*)
f
′
2x
2
x–2+
f
′
1
2
---
4x 1–
2x
2
x–2+
-----------------------------------
§ 47. Промежутки монотонности и экстремумы функции 225
Приравниваем производную (x) нулю:
= 0.
Отсюда получаем ритичесую точу x
0
= . Из выражения (*)
видно, что если x > , то (x) > 0, а если x < , то (x) < 0,
т. е. при переходе через точу x
0
= производная меняет зна
с минуса на плюс. Следовательно, x
0
= — точа минимума,
причем f(x
0
) = . Знаменатель выражения (*) положителен
при x Ý R. Ита, друих ритичесих точе, роме x = ,
фунция f(x) не имеет.
Ответ. f(x) = f = .
Найдите эстремумы данной фунции:
19. f(x) = . 10. f(x) = x + sin 2x.
11. f(x) = . 12. f(x) = .
13. f(x) = 2x
3
+ 3x
2
– 12x + 5. 14. f(x) = .
15. f(x) = 2x
3
– 6x
2
– 18x + 7. 16. f(x) = .
С помощью исследования фунций на эстремум можно ус-
танавливать справедливость неоторых трансцендентных нера-
венств.
Пример 3. Доазать, что при x − 0 справедливо нера-
венство
e
x
– x > 1.
Р е ш е н и е. Рассмотрим фунцию
f(x) = e
x
– 1 – x
и найдем ее эстремум. Решив уравнение f′(x) = 0, т. е. уравне-
ние e
x
– 1 = 0, получаем x = 0.
f
′
1
2
---
4x 1–
2x
2
x–2+
-----------------------------------
1
4
---
1
4
---
f
′
1
4
---
f
′
1
4
---
1
4
---
15
8
------
1
4
---
min
x Ý R
1
4
---
15
8
------
x 2–()
2
x 4+()
4
---------------------------------------- -
xe
xx
2
–
2x
x
2
9+
---------------- -
x
ln x
----------
x
2
2x–2+
x 1–
-------------------------------

224 Г л а в а 9. Производная и ее применения
7. Найдите множество всех значений параметра a, при ото-
рых фунция
f(x) = sin 2x – 8(a – 1) sin x + (4a
2
+ 8a – 14)x
является возрастающей и не имеет ритичесих точе для всех
x Ý R.
8. Найдите всех значения параметра a, при оторых фунция
y(x) = 8ax – a sin 6x – 7x – sin 5x
возрастает и не имеет ритичесих точе для всех x Ý R.
Исследование фнции на эстремм. Говорят, что фун-
ция y = f(x) имеет в точе x
0
масимм (или минимм), если
найдется таая δ-орестность точи x
0
, принадлежащая облас-
ти определения фунции, что для всех x − x
0
, принадлежащих
промежуту (x
0
– δ; x
0
+ δ), выполняется неравенство f(x) < f(x
0
)
(соответственно f(x) > f(x
0
)).
Точи масимума и минимума называют точами эстре-
мма, а значения фунции в этих точах — эстремальными
значениями.
Необходимое словие сществования эстремма фн-
ции. Пусть фунция f(x) дифференцируема на промежуте
(a; b). Тода если в неоторой точе x
0
Ý (a; b) фунция f(x)
достиает эстремума, то (x
0
) = 0.
Достаточное словие сществования эстремма фн-
ции. Пусть фунция определена и непрерывна на промежут-
е (a; b) и на всем промежуте (за ислючением, быть мо-
жет, онечноо числа точе) дифференцируема. Тода если при
переходе через ритичесую точу производная фунции ме-
няет зна, то таая ритичесая точа является точой
эстремума фунции: точой масимума, если зна меняет-
ся с плюса на минус, и точой минимума, если зна меняется
с минуса на плюс.
П р и м е р 2. Найти эстремум фунции
f(x) = .
Р е ш е н и е. Находим производную
(x) = . (*)
f
′
2x
2
x–2+
f
′
1
2
---
4x 1–
2x
2
x–2+
-----------------------------------
§ 47. Промежутки монотонности и экстремумы функции 225
Приравниваем производную (x) нулю:
= 0.
Отсюда получаем ритичесую точу x
0
= . Из выражения (*)
видно, что если x > , то (x) > 0, а если x < , то (x) < 0,
т. е. при переходе через точу x
0
= производная меняет зна
с минуса на плюс. Следовательно, x
0
= — точа минимума,
причем f(x
0
) = . Знаменатель выражения (*) положителен
при x Ý R. Ита, друих ритичесих точе, роме x = ,
фунция f(x) не имеет.
Ответ. f(x) = f = .
Найдите эстремумы данной фунции:
19. f(x) = . 10. f(x) = x + sin 2x.
11. f(x) = . 12. f(x) = .
13. f(x) = 2x
3
+ 3x
2
– 12x + 5. 14. f(x) = .
15. f(x) = 2x
3
– 6x
2
– 18x + 7. 16. f(x) = .
С помощью исследования фунций на эстремум можно ус-
танавливать справедливость неоторых трансцендентных нера-
венств.
Пример 3. Доазать, что при x − 0 справедливо нера-
венство
e
x
– x > 1.
Р е ш е н и е. Рассмотрим фунцию
f(x) = e
x
– 1 – x
и найдем ее эстремум. Решив уравнение f′(x) = 0, т. е. уравне-
ние e
x
– 1 = 0, получаем x = 0.
f
′
1
2
---
4x 1–
2x
2
x–2+
-----------------------------------
1
4
---
1
4
---
f
′
1
4
---
f
′
1
4
---
1
4
---
15
8
------
1
4
---
min
x Ý R
1
4
---
15
8
------
x 2–()
2
x 4+()
4
---------------------------------------- -
xe
xx
2
–
2x
x
2
9+
---------------- -
x
ln x
----------
x
2
2x–2+
x 1–
-------------------------------

226 Г л а в а 9. Производная и ее применения
При x = 0 фунция f(x) достиает своео единственноо ми-
нимума, посольу производная (x) при переходе через точу
x = 0 меняет зна с минуса на плюс. Та а f(0) = 0, то при
всех x − 0 справедливо неравенство f(x) > 0, т. е. e
x
– 1 – x > 0,
или e
x
– x > 1, что и требовалось доазать.
Доажите неравенство:
17. x – < sin x < x при x > 0.
18. cos x > 1 – при x − 0.
19. ln (1 + x) < x при x > 0.
§ 48. Наибольшее и наименьшее
значения функции
Пусть фунция f(x) определена и непрерывна на онечном
промежуте [a; b]. Для отысания наибольшео (наименьшео)
значения фунции необходимо найти все масимумы (миниму-
мы) фунции на промежуте (a; b), выбрать из них наиболь-
ший (наименьший) и сравнить ео со значениями фунции
вточах a и b. Наибольшее (наименьшее) из этих чисел и явля-
ется наибольшим (наименьшим) значением фунции f(x) на про-
межуте [a; b]; оно обозначается f(x) (соответственно
f(x)). При отысании наибольшео или наименьшео
значения фунции может оазаться, что внутри промежута
[a; b] производная существует во всех точах этоо промежута
и ни в одной ео точе не обращается в нуль (т. е. ритичесие
точи фунции отсутствуют). Это означает, что в рассматри-
ваемом промежуте фунция возрастает или убывает и, следо-
вательно, достиает наибольшео и наименьшео значений на
онцах промежута.
П р и м е р 1. Найти наибольшее и наименьшее значения
фунции f(x) = + на промежуте [1; 6].
Решение. Та а
(x) = – ,
f
′
x
3
6
------
x
2
2
------
max
x Ý [a; b]
min
x Ý [a; b]
x
8
---
2
x
---
f
′
1
8
---
2
x
2
------
§ 48. Наибольшее и наименьшее значения функции 227
то единственной ритичесой точой, принадлежащей задан-
ному промежуту, является точа x = 4. Сравнивая значения
фунции в этой точе со значениями фунции на онцах про-
межута, получаем
f(4) = 1, f(1) = 2 , f(6) = 1 ,
т. е. наименьшее значение f(x) достиается в точе x = 4, а
наибольшее — на левом онце промежута (при x = 1).
Ответ. f(x) = f(1) = 2 ; f(x) = f(4) = 1.
Найдите наибольшее и наименьшее значения фунции на
уазанном промежуте:
1. f(x) = x
5
– x
3
+ x + 2, x Ý [–1; 1].
2. f(x) = 3x
4
+ 4x
3
+ 1, x Ý [–2; 1].
3. f(x) = cos
2
sin x, x Ý [0; π].
4. f(x) = cos 2x + sin x, x Ý 0; .
5. f(x) = – sin 2x + cos
3
x – cos x, x Ý –; .
Инода при отысании наибольшео (наименьшео) значе-
ния фунции удобно использовать следующее свойство.
Если непрерывную фунцию F(x) на промежуте [a; b] мож-
но представить в виде F(x) = f(g(x)), де g(x) и f(y)— непрерыв-
ные фунции на промежутах x Ý [a; b] и y Ý [c; d] соответ-
ственно, c = g(x), d = g(x), то
F(x) = f(y)и F(x) = f(y).
П р и м е р 2. Найти наибольшее и наименьшее значения
фунции
F(x) =
на промежуте 0; .
1
8
---
1
12
------
max
x Ý [1; 6]
1
8
---
min
x Ý [1; 6]
x
2
---
1
2
---
π
2
---
x
2
---
1
4
---
1
3
---
π
2
---
π
2
---
min
x Ý [a; b]
max
x Ý [c; d]
max
x Ý [a; b]
max
x Ý [c; d]
min
x Ý [a; b]
min
x Ý [c; d]
sin 2x
sin
π
4
---
x+
-----------------------------
π
2
---
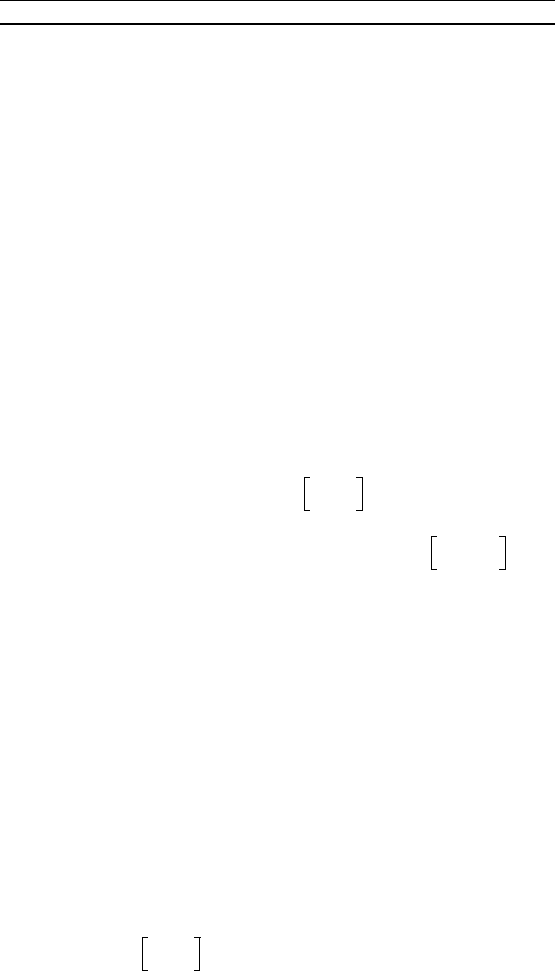
226 Г л а в а 9. Производная и ее применения
При x = 0 фунция f(x) достиает своео единственноо ми-
нимума, посольу производная (x) при переходе через точу
x = 0 меняет зна с минуса на плюс. Та а f(0) = 0, то при
всех x − 0 справедливо неравенство f(x) > 0, т. е. e
x
– 1 – x > 0,
или e
x
– x > 1, что и требовалось доазать.
Доажите неравенство:
17. x – < sin x < x при x > 0.
18. cos x > 1 – при x − 0.
19. ln (1 + x) < x при x > 0.
§ 48. Наибольшее и наименьшее
значения функции
Пусть фунция f(x) определена и непрерывна на онечном
промежуте [a; b]. Для отысания наибольшео (наименьшео)
значения фунции необходимо найти все масимумы (миниму-
мы) фунции на промежуте (a; b), выбрать из них наиболь-
ший (наименьший) и сравнить ео со значениями фунции
вточах a и b. Наибольшее (наименьшее) из этих чисел и явля-
ется наибольшим (наименьшим) значением фунции f(x) на про-
межуте [a; b]; оно обозначается f(x) (соответственно
f(x)). При отысании наибольшео или наименьшео
значения фунции может оазаться, что внутри промежута
[a; b] производная существует во всех точах этоо промежута
и ни в одной ео точе не обращается в нуль (т. е. ритичесие
точи фунции отсутствуют). Это означает, что в рассматри-
ваемом промежуте фунция возрастает или убывает и, следо-
вательно, достиает наибольшео и наименьшео значений на
онцах промежута.
П р и м е р 1. Найти наибольшее и наименьшее значения
фунции f(x) = + на промежуте [1; 6].
Решение. Та а
(x) = – ,
f
′
x
3
6
------
x
2
2
------
max
x Ý [a; b]
min
x Ý [a; b]
x
8
---
2
x
---
f
′
1
8
---
2
x
2
------
§ 48. Наибольшее и наименьшее значения функции 227
то единственной ритичесой точой, принадлежащей задан-
ному промежуту, является точа x = 4. Сравнивая значения
фунции в этой точе со значениями фунции на онцах про-
межута, получаем
f(4) = 1, f(1) = 2 , f(6) = 1 ,
т. е. наименьшее значение f(x) достиается в точе x = 4, а
наибольшее — на левом онце промежута (при x = 1).
Ответ. f(x) = f(1) = 2 ; f(x) = f(4) = 1.
Найдите наибольшее и наименьшее значения фунции на
уазанном промежуте:
1. f(x) = x
5
– x
3
+ x + 2, x Ý [–1; 1].
2. f(x) = 3x
4
+ 4x
3
+ 1, x Ý [–2; 1].
3. f(x) = cos
2
sin x, x Ý [0; π].
4. f(x) = cos 2x + sin x, x Ý 0; .
5. f(x) = – sin 2x + cos
3
x – cos x, x Ý –; .
Инода при отысании наибольшео (наименьшео) значе-
ния фунции удобно использовать следующее свойство.
Если непрерывную фунцию F(x) на промежуте [a; b] мож-
но представить в виде F(x) = f(g(x)), де g(x) и f(y)— непрерыв-
ные фунции на промежутах x Ý [a; b] и y Ý [c; d] соответ-
ственно, c = g(x), d = g(x), то
F(x) = f(y)и F(x) = f(y).
П р и м е р 2. Найти наибольшее и наименьшее значения
фунции
F(x) =
на промежуте 0; .
1
8
---
1
12
------
max
x Ý [1; 6]
1
8
---
min
x Ý [1; 6]
x
2
---
1
2
---
π
2
---
x
2
---
1
4
---
1
3
---
π
2
---
π
2
---
min
x Ý [a; b]
max
x Ý [c; d]
max
x Ý [a; b]
max
x Ý [c; d]
min
x Ý [a; b]
min
x Ý [c; d]
sin 2x
sin
π
4
---
x+
-----------------------------
π
2
---

228 Г л а в а 9. Производная и ее применения
Р е ш е н и е. Используя формулы
sin + x = (sin x + cos x), sin 2x = (sin x + cos x)
2
– 1,
представим данную фунцию в виде сложной фунции
F(x)=f(g(x)), де
f(y) = , g(x) = sin x + cos x.
Будем исать наибольшее и наименьшее значения фунции
g(x). Критичесими точами этой фунции являются орни
уравнения
cos x – sin x = 0,
из оторых промежуту 0; принадлежит тольо x = .
Сравнивая значения g(0), g и g , залючаем, что об-
ласть изменения фунции g(x) есть промежуто [1; ]. Диф-
ференцируя, имеем
(y) = 1 + > 0
на всей области определения фунции f(y), в том числе и при
y Ý [1; ]. Следовательно, фунция f(y) возрастает на проме-
жуте [1; ] и достиает наибольшео и наименьшео значе-
ния соответственно на правом и левом онце промежута:
f(y) = f( ) = 1, f(y) = f(1) = 0.
Эти же значения являются наибольшим и наименьшим и для
исходной фунции F(x).
Ответ. F(x) = 1, F(x) = 0.
Найдите наибольшее и наименьшее значения фунции:
6. f(x) = , x Ý π; .
7. f(x) = – , x Ý R.
π
4
---
2
2
-------
y
2
1–
y
----------------
2
π
2
---
π
4
---
π
4
---
π
2
---
2
f
′
2
1
y
2
----- -
2
2
y Ý [1; 2]
max 2
g Ý [1; 2]
min
max
x Ý [0; π/2]
min
x Ý [0; π/2]
sin 2x
sin
π
4
---
x+
-------------------------------
3π
2
------ -
1
sin x 4+
----------------------- -
1
cos x 4–
-----------------------
§ 48. Наибольшее и наименьшее значения функции 229
8. f(x) = tg x + ctg x, x Ý ; .
9. Найдите наименьшее значение фунции
f(x) =
на промежуте [0; π].
Перейдем отысанию наибольшео и наименьшео значе-
ний фунций, содержащих зна модуля.
П р и м е р 3. Найти наибольшее и наименьшее значения
фунции
f(x) = | x
2
– 5x + 6 | (*)
на промежуте [0; 2,4].
Р е ш е н и е. Чтобы расрыть модуль в выражении (*), най-
дем орни уравнения f(x) = 0. Решив уравнение x
2
– 5x + 6 = 0,
получаем x = 2, x = 3. Таим образом,
f(x) = (**)
Из формул (**) видно, что на исследуемом промежуте [0; 2,4]
фунция f(x) допусает два представления в зависимости от
значений арумента:
f(x) =
Найдем производную фунции f(x):
(x) =
Если x Ý [0; 2), то (x) < 0 и, следовательно, f(x) убывает, а
если x Ý (2; 2,4], то (x) > 0 и, значит, f(x) возрастает; точа
x = 2 — ритичесая, та а производная (x) в этой точе
не существует. Сравнивая значения фунции на онцах про-
межута [0; 2,4] с ее значением в ритичесой точе, залюча-
ем, что
f(x) = f(0) = 6, f(x) = f(2) = 0.
Ответ. f(x) = f(0) = 6, f(x) = f(2) = 0.
π
6
---
π
3
---
2cosx+
sin x
------------------------
2
–(x
2
– 5x + 6, x Ý (–×; 2) Ÿ (3; +×);
–(x
2
– 5x + 6), x Ý [2; 3].
–(x
2
– 5x + 6, x Ý [0; 2],
–(x
2
– 5x + 6), x Ý (2; 2,4].
f
′
–(2x – 5, x Ý [0; 2),
–(2x – 5), x Ý (2; 2,4].
f
′
f
′
f
′
max
x Ý [0; 2,4]
min
x Ý [0; 2,4]
max
x Ý [0; 2,4]
min
x Ý [0; 2,4]

228 Г л а в а 9. Производная и ее применения
Р е ш е н и е. Используя формулы
sin + x = (sin x + cos x), sin 2x = (sin x + cos x)
2
– 1,
представим данную фунцию в виде сложной фунции
F(x)=f(g(x)), де
f(y) = , g(x) = sin x + cos x.
Будем исать наибольшее и наименьшее значения фунции
g(x). Критичесими точами этой фунции являются орни
уравнения
cos x – sin x = 0,
из оторых промежуту 0; принадлежит тольо x = .
Сравнивая значения g(0), g и g , залючаем, что об-
ласть изменения фунции g(x) есть промежуто [1; ]. Диф-
ференцируя, имеем
(y) = 1 + > 0
на всей области определения фунции f(y), в том числе и при
y Ý [1; ]. Следовательно, фунция f(y) возрастает на проме-
жуте [1; ] и достиает наибольшео и наименьшео значе-
ния соответственно на правом и левом онце промежута:
f(y) = f( ) = 1, f(y) = f(1) = 0.
Эти же значения являются наибольшим и наименьшим и для
исходной фунции F(x).
Ответ. F(x) = 1, F(x) = 0.
Найдите наибольшее и наименьшее значения фунции:
6. f(x) = , x Ý π; .
7. f(x) = – , x Ý R.
π
4
---
2
2
-------
y
2
1–
y
----------------
2
π
2
---
π
4
---
π
4
---
π
2
---
2
f
′
2
1
y
2
----- -
2
2
y Ý [1; 2]
max 2
g Ý [1; 2]
min
max
x Ý [0; π/2]
min
x Ý [0; π/2]
sin 2x
sin
π
4
---
x+
-------------------------------
3π
2
------ -
1
sin x 4+
----------------------- -
1
cos x 4–
-----------------------
§ 48. Наибольшее и наименьшее значения функции 229
8. f(x) = tg x + ctg x, x Ý ; .
9. Найдите наименьшее значение фунции
f(x) =
на промежуте [0; π].
Перейдем отысанию наибольшео и наименьшео значе-
ний фунций, содержащих зна модуля.
П р и м е р 3. Найти наибольшее и наименьшее значения
фунции
f(x) = | x
2
– 5x + 6 | (*)
на промежуте [0; 2,4].
Р е ш е н и е. Чтобы расрыть модуль в выражении (*), най-
дем орни уравнения f(x) = 0. Решив уравнение x
2
– 5x + 6 = 0,
получаем x = 2, x = 3. Таим образом,
f(x) = (**)
Из формул (**) видно, что на исследуемом промежуте [0; 2,4]
фунция f(x) допусает два представления в зависимости от
значений арумента:
f(x) =
Найдем производную фунции f(x):
(x) =
Если x Ý [0; 2), то (x) < 0 и, следовательно, f(x) убывает, а
если x Ý (2; 2,4], то (x) > 0 и, значит, f(x) возрастает; точа
x = 2 — ритичесая, та а производная (x) в этой точе
не существует. Сравнивая значения фунции на онцах про-
межута [0; 2,4] с ее значением в ритичесой точе, залюча-
ем, что
f(x) = f(0) = 6, f(x) = f(2) = 0.
Ответ. f(x) = f(0) = 6, f(x) = f(2) = 0.
π
6
---
π
3
---
2cosx+
sin x
------------------------
2
–(x
2
– 5x + 6, x Ý (–×; 2) Ÿ (3; +×);
–(x
2
– 5x + 6), x Ý [2; 3].
–(x
2
– 5x + 6, x Ý [0; 2],
–(x
2
– 5x + 6), x Ý (2; 2,4].
f
′
–(2x – 5, x Ý [0; 2),
–(2x – 5), x Ý (2; 2,4].
f
′
f
′
f
′
max
x Ý [0; 2,4]
min
x Ý [0; 2,4]
max
x Ý [0; 2,4]
min
x Ý [0; 2,4]
