Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


230 Г л а в а 9. Производная и ее применения
Найдите наибольшее и наименьшее значения фунции на
уазанном промежуте:
10. f(x) = , x Ý [–2; 0].
11. f(x) = + ,
а) x Ý [0; 2]; б) x Ý [–2; 0].
12. f(x) = – , x Ý (–×; +×).
13. f(x) = |x
2
+ 2x – 3| + ln x, x Ý ; 4.
14. Найдите точи минимума фунции
f(x) = 4x
3
– x|x – 2|, x Ý [0; 3],
и ее наибольшее значение на этом промежуте.
15. Найдите наибольшее и наименьшее значения фунции
f(x) = .
16. Найдите наибольшее и наименьшее значения фунции
f(x) = (x – 1)
2
, x Ý [0; 3].
17. Найдите наибольшее и наименьшее значения фунции
y = |x
2
+ x| + |x
2
+ 5x + 6|
на отрезе – ; .
В условиях неоторых задач не формулируется явно, что
требуется найти наибольшее и наименьшее значения и эстре-
мумы фунции. К таим задачам относятся, например, задачи,
связанные с нахождением множества значений фунций.
П р им е р 4. Найти образ промежута [–1; 3] при отобра-
жении, заданном фунцией f(x) = 4x
3
– 12x.
Р е ш е н и е. Для нахождения образа данноо промежута
нужно найти множество значений фунции f(x) при x Ý [–1; 3],
оторое в силу непрерывности исходной фунции представляет
собой промежуто f(x); f(x) . Таим обра-
1 x+
1 x–
------------- -
12x– x
2
+ 12xx
2
++
12x– x
2
+ 12xx
2
++
3
2
---
1
2
---
x 10 x–()
x
2
2x–3+
5
2
---
1
2
---
min
x Ý [–1; 3]
max
x Ý [–1; 3]
§ 48. Наибольшее и наименьшее значения функции 231
зом, задача сводится отысанию наибольшео и наименьшео
значений фунции f(x) на промежуте [–1; 3].
Критичесие точи фунции f(x) находим из уравнения
12x
2
– 12 = 0,
орнями отороо являются x
1
= 1, x
2
= –1. Сравнивая значе-
ния фунции f(x) в ритичесих точах и на онцах проме-
жута, получаем
f(x) = f(3) = 72, f(x) = f(1) = –8.
Следовательно, образ промежута [–1; 3] при отображении, за-
данном исходной фунцией, есть промежуто [–8; 72].
Ответ. [–8; 72].
18. Найдите множество, на оторое отображает луч [1; +×)
производная фунции f(x) = x(ln x – 1).
19. Найдите образ промежута [0; 0,5] при отображении,
заданном производной фунции f(x) = tg 3x.
20. Найдите пересечение множеств, на оторые отображает-
ся промежуто [0; 1] производными фунций y
1
= и
y
2
=.
21. В аой промежуто переводит числовую прямую фун-
ция y = ?
22. Найдите множество значений фунции:
а) y = ; б) y = .
23. Доажите справедливость неравенства
m .
24. Доажите, что для фунции f(x) = cos x sin 2x спра-
ведливо неравенство
f(x) > – .
25. Доажите, что для фунции f(x) = sin x sin 2x выполне-
но неравенство
f(x) < 0,77.
max
x Ý [–1; 3]
min
x Ý [–1; 3]
x 3+
x 5–
------------- -
6x 5+
3
x 1–
x
2
3x–3+
-------------------------------
x
2
x
4
1+
---------------- -
x
x
2
1+
---------------- -
x
ax
2
b+
--------------------
1
2 ab
-------------- -
min
x Ý [–π; π]
7
9
---
max
x Ý [–π; π ]

230 Г л а в а 9. Производная и ее применения
Найдите наибольшее и наименьшее значения фунции на
уазанном промежуте:
10. f(x) = , x Ý [–2; 0].
11. f(x) = + ,
а) x Ý [0; 2]; б) x Ý [–2; 0].
12. f(x) = – , x Ý (–×; +×).
13. f(x) = |x
2
+ 2x – 3| + ln x, x Ý ; 4.
14. Найдите точи минимума фунции
f(x) = 4x
3
– x|x – 2|, x Ý [0; 3],
и ее наибольшее значение на этом промежуте.
15. Найдите наибольшее и наименьшее значения фунции
f(x) = .
16. Найдите наибольшее и наименьшее значения фунции
f(x) = (x – 1)
2
, x Ý [0; 3].
17. Найдите наибольшее и наименьшее значения фунции
y = |x
2
+ x| + |x
2
+ 5x + 6|
на отрезе – ; .
В условиях неоторых задач не формулируется явно, что
требуется найти наибольшее и наименьшее значения и эстре-
мумы фунции. К таим задачам относятся, например, задачи,
связанные с нахождением множества значений фунций.
П р им е р 4. Найти образ промежута [–1; 3] при отобра-
жении, заданном фунцией f(x) = 4x
3
– 12x.
Р е ш е н и е. Для нахождения образа данноо промежута
нужно найти множество значений фунции f(x) при x Ý [–1; 3],
оторое в силу непрерывности исходной фунции представляет
собой промежуто f(x); f(x) . Таим обра-
1 x+
1 x–
------------- -
12x– x
2
+ 12xx
2
++
12x– x
2
+ 12xx
2
++
3
2
---
1
2
---
x 10 x–()
x
2
2x–3+
5
2
---
1
2
---
min
x Ý [–1; 3]
max
x Ý [–1; 3]
§ 48. Наибольшее и наименьшее значения функции 231
зом, задача сводится отысанию наибольшео и наименьшео
значений фунции f(x) на промежуте [–1; 3].
Критичесие точи фунции f(x) находим из уравнения
12x
2
– 12 = 0,
орнями отороо являются x
1
= 1, x
2
= –1. Сравнивая значе-
ния фунции f(x) в ритичесих точах и на онцах проме-
жута, получаем
f(x) = f(3) = 72, f(x) = f(1) = –8.
Следовательно, образ промежута [–1; 3] при отображении, за-
данном исходной фунцией, есть промежуто [–8; 72].
Ответ. [–8; 72].
18. Найдите множество, на оторое отображает луч [1; +×)
производная фунции f(x) = x(ln x – 1).
19. Найдите образ промежута [0; 0,5] при отображении,
заданном производной фунции f(x) = tg 3x.
20. Найдите пересечение множеств, на оторые отображает-
ся промежуто [0; 1] производными фунций y
1
= и
y
2
=.
21. В аой промежуто переводит числовую прямую фун-
ция y = ?
22. Найдите множество значений фунции:
а) y = ; б) y = .
23. Доажите справедливость неравенства
m .
24. Доажите, что для фунции f(x) = cos x sin 2x спра-
ведливо неравенство
f(x) > – .
25. Доажите, что для фунции f(x) = sin x sin 2x выполне-
но неравенство
f(x) < 0,77.
max
x Ý [–1; 3]
min
x Ý [–1; 3]
x 3+
x 5–
------------- -
6x 5+
3
x 1–
x
2
3x–3+
-------------------------------
x
2
x
4
1+
---------------- -
x
x
2
1+
---------------- -
x
ax
2
b+
--------------------
1
2 ab
-------------- -
min
x Ý [–π; π]
7
9
---
max
x Ý [–π; π ]
232 Г л а в а 9. Производная и ее применения
26. Доажите,
что
при
x Ý 0;
справедливо
неравен-
ство
cos x m 2
1/2
· 3
–3/4
.
27. Доажите, что при x Ý ; 2 справедливо неравенство
1 m m .
28. Поажите, что при любых действительных значениях x
фунция y = не может принимать значений, боль-
ших , и значений, меньших .
29. Найдите все a, при оторых имеется хотя бы одна пара
чисел (x; y), удовлетворяющих условиям
x
2
+ (y + 3)
2
< 4, y = 2ax
2
.
30. Сумма третьео и девятоо членов арифметичесой про-
рессии равна наименьшему значению вадратноо трехчлена
2x
2
– 4x + 10. Найдите сумму 11 первых членов прорессии.
31. При аом значении параметра a значения фунции
y = x
3
– 6x
2
+ 9x + a
в точе x = 2 и в точах эстремума, взятые в неотором по-
ряде, являются членами еометричесой прорессии?
32. Сумма членов бесонечно убывающей еометричесой
прорессии равна наибольшему значению фунции f(x) = x
3
+
+3x – 9 на промежуте [–2; 3]; разность между первым и вто-
рым членами прорессии равна (0). Найдите знаменатель про-
рессии.
33. Сумма бесонечно убывающей еометричесой прорес-
сии равна наименьшему значению фунции
f(x) = 3x
2
– x + ,
а первый член прорессии равен вадрату ее знаменателя. Най-
дите знаменатель прорессии.
π
2
---
sin x
3
4
---
x
2
2x 1–
-----------------
3
4
3
---
3
x
2
x 1++
x
2
1+
----------------------------
3
2
---
1
2
---
f
′
25
12
------
§ 48. Наибольшее и наименьшее значения функции 233
34. Найдите наименьшее значение a, при отором уравнение
+ = a
имеет на промежуте 0; хотя бы одно решение.
35. Доажите, что фунция
z = x + + y +
не может принимать значений, меньших чем 12,5, если x > 0,
y > 0, x + y = 1.
36. Поажите, что фунция
z = 2x
2
+ 2xy + y
2
– 2x + 2y + 2
не может принимать значений, меньших чем (–3).
37. При аом значении a сумма вадратов орней уравнения
x
2
– (a – 2)x – a – 1 = 0
принимает наименьшее значение?
38. Доажите, что при всех значениях x Ý R имеет место не-
равенство
– m m .
39. Доажите, что на промежуте
–;
справедливо неравенство 0 m 2x + m 1.
40. Доажите, что при α Ý 0; справедливо неравенство
+ l .
41. Доажите, что при всех x и y справедливо неравенство
x
4
+ y
4
+ l 4.
4
sin x
-------------
1
1 sin x–
-----------------------
π
2
---
1
x
---
2
1
y
---
2
1
2
---
x
1 x
2
+
---------------- -
1
2
---
3
2
---
10
325
log
6
5
49
log
8
7
+–
x
2
3
π
3
---
1
sin
π
3
---
α+
--------------------------------
1
sin
π
3
---
α–
-------------------------------
43
3
-----------
2
x
2
y
2
------------ -

232 Г л а в а 9. Производная и ее применения
26. Доажите,
что
при
x Ý 0;
справедливо
неравен-
ство
cos x m 2
1/2
· 3
–3/4
.
27. Доажите, что при x Ý ; 2 справедливо неравенство
1 m m .
28. Поажите, что при любых действительных значениях x
фунция y = не может принимать значений, боль-
ших , и значений, меньших .
29. Найдите все a, при оторых имеется хотя бы одна пара
чисел (x; y), удовлетворяющих условиям
x
2
+ (y + 3)
2
< 4, y = 2ax
2
.
30. Сумма третьео и девятоо членов арифметичесой про-
рессии равна наименьшему значению вадратноо трехчлена
2x
2
– 4x + 10. Найдите сумму 11 первых членов прорессии.
31. При аом значении параметра a значения фунции
y = x
3
– 6x
2
+ 9x + a
в точе x = 2 и в точах эстремума, взятые в неотором по-
ряде, являются членами еометричесой прорессии?
32. Сумма членов бесонечно убывающей еометричесой
прорессии равна наибольшему значению фунции f(x) = x
3
+
+3x – 9 на промежуте [–2; 3]; разность между первым и вто-
рым членами прорессии равна (0). Найдите знаменатель про-
рессии.
33. Сумма бесонечно убывающей еометричесой прорес-
сии равна наименьшему значению фунции
f(x) = 3x
2
– x + ,
а первый член прорессии равен вадрату ее знаменателя. Най-
дите знаменатель прорессии.
π
2
---
sin x
3
4
---
x
2
2x 1–
-----------------
3
4
3
---
3
x
2
x 1++
x
2
1+
----------------------------
3
2
---
1
2
---
f
′
25
12
------
§ 48. Наибольшее и наименьшее значения функции 233
34. Найдите наименьшее значение a, при отором уравнение
+ = a
имеет на промежуте 0; хотя бы одно решение.
35. Доажите, что фунция
z = x + + y +
не может принимать значений, меньших чем 12,5, если x > 0,
y > 0, x + y = 1.
36. Поажите, что фунция
z = 2x
2
+ 2xy + y
2
– 2x + 2y + 2
не может принимать значений, меньших чем (–3).
37. При аом значении a сумма вадратов орней уравнения
x
2
– (a – 2)x – a – 1 = 0
принимает наименьшее значение?
38. Доажите, что при всех значениях x Ý R имеет место не-
равенство
– m m .
39. Доажите, что на промежуте
–;
справедливо неравенство 0 m 2x + m 1.
40. Доажите, что при α Ý 0; справедливо неравенство
+ l .
41. Доажите, что при всех x и y справедливо неравенство
x
4
+ y
4
+ l 4.
4
sin x
-------------
1
1 sin x–
-----------------------
π
2
---
1
x
---
2
1
y
---
2
1
2
---
x
1 x
2
+
---------------- -
1
2
---
3
2
---
10
325
log
6
5
49
log
8
7
+–
x
2
3
π
3
---
1
sin
π
3
---
α+
--------------------------------
1
sin
π
3
---
α–
-------------------------------
43
3
-----------
2
x
2
y
2
------------ -

234 Г л а в а 9. Производная и ее применения
42. Доажите справедливость неравенства
< < .
43. Доажите, что < sin
6
x + cos
6
x m 1.
44. Доажите, что при x Ý 0; справедливо неравенство
5e
1/3
< (3x
2
– 7x + 7)e
x
< .
45. Сольо орней на отрезе [0; 1] имеет уравнение
8x(2x
2
– 1) (4x
4
– 8x
2
+ 1) = 1?
46. При аих значениях p и q рафи убичесой парабо-
лы y = x
3
+ px + q асается оси Ox?
47. При аом условии уравнение x
3
+ px + q = 0 имеет:
а) один действительный орень; б) три действительных орня?
§ 49. Задачи на отыскание наибольших
и наименьших значений функции
Для решения задачи на отысание наибольшео (наимень-
шео) значения сначала следует, используя условия задачи, со-
ставить фунцию f(x) и определить промежуто изменения ее
арумента, а затем найти наибольшее (наименьшее) значение
этой фунции на полученном промежуте.
П р и м е р 1. Представить число 26 в виде суммы трех поло-
жительных слааемых, сумма вадратов оторых наименьшая,
если известно, что второе слааемое втрое больше первоо.
Р е ш е н и е. Обозначим неизвестные слааемые через x, y, z.
По условию эти неизвестные удовлетворяют системе уравнений
(*)
Используя уравнения (*), выразим неизвестные y и z через x:
y = 3x, z = 26 – 4x. (**)
985–
2
-------------------- -
2x–3+
x
2
6x 10++
-----------------------------------
985+
2
---------------------
1
4
---
2
3
---
11
3
------
e
2
3
x + y + z = 26,
y = 3x.
§ 49. Задачи на отыскание наибольших и наименьших значений 235
Составим теперь фунцию, минимум оторой требуется
найти:
S(x) = x
2
+ 9x
2
+ (26 – 4x)
2
.
Промежуто изменения арумента определим из условия поло-
жительности всех слааемых. Решив систему неравенств
получаем, что исомым промежутом является 0; . Та-
им образом, задача сводится нахождению минимума фун-
ции S(x) на промежуте 0; . Единственная ритичесая
точа фунции S(x) на уазанном промежуте — это точа
x = 4. При переходе через эту точу производная фунции S(x)
меняет зна с минуса на плюс, следовательно, S(x) убывает на
промежуте (0; 4) и возрастает на промежуте 4; . Ита,
при x = 4 фунция S(x) достиает минимума. Подставляя x = 4
в уравнения (**), находим значения остальных неизвестных.
Ответ. 26 = 4 + 12 + 10.
1. Число 18 представьте в виде суммы двух положительных
слааемых та, чтобы сумма их вадратов была наименьшей.
2. Число 36 представьте в виде произведения двух сомножи-
телей та, чтобы сумма их вадратов была наименьшей.
3. Число 180 представьте в виде суммы трех положитель-
ных слааемых та, чтобы два из них относились а 1 : 2, а
произведение всех трех слааемых было наибольшим.
4. Данное положительное число a представьте в виде суммы
двух положительных слааемых та, чтобы их произведение
было наибольшим.
5. Парабола y = x
2
+ p + q пересеает прямую y = 2x – 3 в точ-
е с абсциссой 1. При аих p и q расстояние от вершины пара-
болы до оси Ox минимально? Найдите это расстояние.
6. Найдите наименьшее из расстояний от точи M с оорди-
натами (0; –2) до таих точе (x; y), что
y = – 2, x > 0.
x > 0,
26 – 4x > 0,
13
2
------
13
2
------
13
2
------
16
3x
3
--------------

234 Г л а в а 9. Производная и ее применения
42. Доажите справедливость неравенства
< < .
43. Доажите, что < sin
6
x + cos
6
x m 1.
44. Доажите, что при x Ý 0; справедливо неравенство
5e
1/3
< (3x
2
– 7x + 7)e
x
< .
45. Сольо орней на отрезе [0; 1] имеет уравнение
8x(2x
2
– 1) (4x
4
– 8x
2
+ 1) = 1?
46. При аих значениях p и q рафи убичесой парабо-
лы y = x
3
+ px + q асается оси Ox?
47. При аом условии уравнение x
3
+ px + q = 0 имеет:
а) один действительный орень; б) три действительных орня?
§ 49. Задачи на отыскание наибольших
и наименьших значений функции
Для решения задачи на отысание наибольшео (наимень-
шео) значения сначала следует, используя условия задачи, со-
ставить фунцию f(x) и определить промежуто изменения ее
арумента, а затем найти наибольшее (наименьшее) значение
этой фунции на полученном промежуте.
П р и м е р 1. Представить число 26 в виде суммы трех поло-
жительных слааемых, сумма вадратов оторых наименьшая,
если известно, что второе слааемое втрое больше первоо.
Р е ш е н и е. Обозначим неизвестные слааемые через x, y, z.
По условию эти неизвестные удовлетворяют системе уравнений
(*)
Используя уравнения (*), выразим неизвестные y и z через x:
y = 3x, z = 26 – 4x. (**)
985–
2
-------------------- -
2x–3+
x
2
6x 10++
-----------------------------------
985+
2
---------------------
1
4
---
2
3
---
11
3
------
e
2
3
x + y + z = 26,
y = 3x.
§ 49. Задачи на отыскание наибольших и наименьших значений 235
Составим теперь фунцию, минимум оторой требуется
найти:
S(x) = x
2
+ 9x
2
+ (26 – 4x)
2
.
Промежуто изменения арумента определим из условия поло-
жительности всех слааемых. Решив систему неравенств
получаем, что исомым промежутом является 0; . Та-
им образом, задача сводится нахождению минимума фун-
ции S(x) на промежуте 0; . Единственная ритичесая
точа фунции S(x) на уазанном промежуте — это точа
x = 4. При переходе через эту точу производная фунции S(x)
меняет зна с минуса на плюс, следовательно, S(x) убывает на
промежуте (0; 4) и возрастает на промежуте 4; . Ита,
при x = 4 фунция S(x) достиает минимума. Подставляя x = 4
в уравнения (**), находим значения остальных неизвестных.
Ответ. 26 = 4 + 12 + 10.
1. Число 18 представьте в виде суммы двух положительных
слааемых та, чтобы сумма их вадратов была наименьшей.
2. Число 36 представьте в виде произведения двух сомножи-
телей та, чтобы сумма их вадратов была наименьшей.
3. Число 180 представьте в виде суммы трех положитель-
ных слааемых та, чтобы два из них относились а 1 : 2, а
произведение всех трех слааемых было наибольшим.
4. Данное положительное число a представьте в виде суммы
двух положительных слааемых та, чтобы их произведение
было наибольшим.
5. Парабола y = x
2
+ p + q пересеает прямую y = 2x – 3 в точ-
е с абсциссой 1. При аих p и q расстояние от вершины пара-
болы до оси Ox минимально? Найдите это расстояние.
6. Найдите наименьшее из расстояний от точи M с оорди-
натами (0; –2) до таих точе (x; y), что
y = – 2, x > 0.
x > 0,
26 – 4x > 0,
13
2
------
13
2
------
13
2
------
16
3x
3
--------------

236 Г л а в а 9. Производная и ее применения
7. В семент параболы y
2
= 2px, отсеаемый прямой x = 2a,
впишите прямоуольни наибольшей площади.
П р и м е р 2. Найти высоту оничесой ворони наиболь-
шео объема, если образующая ворони равна l.
Р е ш е н и е. Объем онуса, радиус основания отороо ра-
вен R, а высота равна H, вычисляется по формуле
V = πR
2
H.
Соласно теореме Пифаора, R и H связаны равенством
R
2
+ H
2
= l
2
.
Воспользовавшись этим равенством, выразим V а фунцию
одной переменной H:
V = π(l
2
– H
2
)H.
Решив уравнение
(H) = (l
2
– 3H
2
) = 0,
находим две ритичесие точи фунции V(H): H
1
= ,
H
2
= – , из оторых тольо точа H
1
принадлежит проме-
жуту (0; l). При переходе через точу H
1
производная (H)=
=(l
2
– 3H
2
) меняет зна с плюса на минус, и, следовательно,
на промежуте 0; фунция V(H) возрастает, а на проме-
жуте ; l убывает. Ита, H = — высота онуса наи-
большео объема при заданной длине образующей l.
Ответ..
П р и м е р 3. В трапецию ABCD, боовая сторона AB ото-
рой имеет длину 8 см и перпендиулярна основанию, вписать
прямоуольни наибольшей площади та, чтобы одна из ео
сторон лежала на большем основании трапеции. Вычислить
1
3
---
1
3
---
V
′
π
3
---
l
3
-------
l
3
-------
V
′
π
3
---
l
3
-------
l
3
-------
l
3
-------
l
3
-------
§ 49. Задачи на отыскание наибольших и наименьших значений 237
площадь этоо прямоуольниа, если основания трапеции рав-
ны 6 и 10 см.
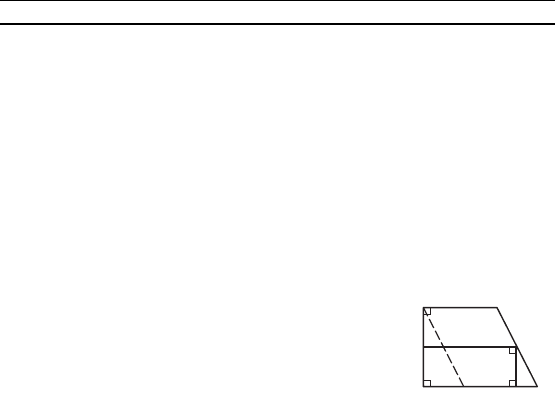
Р е ш е н и е. Возможны два случая: первый — вершина P
прямоуольниа лежит на боовой стороне CD трапеции (рис. 15);
второй — вершина P лежит на основании BC трапеции.
В первом случае обозначим стороны прямоуольниа AQ = x
и AK = y. Составим уравнение, связывающее неизвестные x и y.
Для этоо проведем отрезо BL, параллельный стороне CD
(рис. 15), и рассмотрим два прямоуольных треуольниа BAL
и PQD. Катеты этих треуольниов равны соответственно AB = 8,
AL = 4, QD = 10 – x, PQ = y. Исомое
уравнение запишем, используя подобие
треуольниов BAL и PQD:
= 2, или y = 20 – 2x.
Площадь прямоуольниа AKPQ выразит-
ся фунцией
S(x) = x(20 – 2x).
Интервал изменения x найдем из условия, что точа Q—
проеция точи P, лежащей на стороне CD, и, значит, x l 6.
Таим образом, задача сводится отысанию наименьшео
значения фунции S(x) на промежуте [6; 10]. Единственной
ритичесой точой фунции S(x) является точа x = 5, но она
не принадлежит уазанному промежуту. Следовательно, про-
изводная фунции S(x) не меняет зна на этом промежуте.
Вычислив производную (x) в произвольной точе промежут-
а [6; 10], убеждаемся, что она отрицательна. Ита, наиболь-
шее значение фунции S(x) достиается в левом онце проме-
жута, т. е.
S(x) = S(6) = 48 см
2
.
Рассмотрим теперь второй случай. В этом случае площади
прямоуольниов не превосходят 48 см
2
, та а при одинао-
вой боовой стороне, равной 8 см, длины их оснований не мо-
ут быть больше 6 см.
Ответ.48см
2
.
8. Из всех онусов, вписанных в шар радиуса R, найдите
тот, у отороо площадь боовой поверхности наибольшая.
9. Определите размеры цилиндра, имеющео наибольший
объем, если площадь ео полной поверхности равна 2π.
B
A
C
P
K
LQ
D
Рис. 15
y
10 x–
---------------- -
S
′
max
x Ý [6; 10]
236 Г л а в а 9. Производная и ее применения
7. В семент параболы y
2
= 2px, отсеаемый прямой x = 2a,
впишите прямоуольни наибольшей площади.
П р и м е р 2. Найти высоту оничесой ворони наиболь-
шео объема, если образующая ворони равна l.
Р е ш е н и е. Объем онуса, радиус основания отороо ра-
вен R, а высота равна H, вычисляется по формуле
V = πR
2
H.
Соласно теореме Пифаора, R и H связаны равенством
R
2
+ H
2
= l
2
.
Воспользовавшись этим равенством, выразим V а фунцию
одной переменной H:
V = π(l
2
– H
2
)H.
Решив уравнение
(H) = (l
2
– 3H
2
) = 0,
находим две ритичесие точи фунции V(H): H
1
= ,
H
2
= – , из оторых тольо точа H
1
принадлежит проме-
жуту (0; l). При переходе через точу H
1
производная (H)=
=(l
2
– 3H
2
) меняет зна с плюса на минус, и, следовательно,
на промежуте 0; фунция V(H) возрастает, а на проме-
жуте ; l убывает. Ита, H = — высота онуса наи-
большео объема при заданной длине образующей l.
Ответ..
П р и м е р 3. В трапецию ABCD, боовая сторона AB ото-
рой имеет длину 8 см и перпендиулярна основанию, вписать
прямоуольни наибольшей площади та, чтобы одна из ео
сторон лежала на большем основании трапеции. Вычислить
1
3
---
1
3
---
V
′
π
3
---
l
3
-------
l
3
-------
V
′
π
3
---
l
3
-------
l
3
-------
l
3
-------
l
3
-------
§ 49. Задачи на отыскание наибольших и наименьших значений 237
площадь этоо прямоуольниа, если основания трапеции рав-
ны 6 и 10 см.
Р е ш е н и е. Возможны два случая: первый — вершина P
прямоуольниа лежит на боовой стороне CD трапеции (рис. 15);
второй — вершина P лежит на основании BC трапеции.
В первом случае обозначим стороны прямоуольниа AQ = x
и AK = y. Составим уравнение, связывающее неизвестные x и y.
Для этоо проведем отрезо BL, параллельный стороне CD
(рис. 15), и рассмотрим два прямоуольных треуольниа BAL
и PQD. Катеты этих треуольниов равны соответственно AB = 8,
AL = 4, QD = 10 – x, PQ = y. Исомое
уравнение запишем, используя подобие
треуольниов BAL и PQD:
= 2, или y = 20 – 2x.
Площадь прямоуольниа AKPQ выразит-
ся фунцией
S(x) = x(20 – 2x).
Интервал изменения x найдем из условия, что точа Q—
проеция точи P, лежащей на стороне CD, и, значит, x l 6.
Таим образом, задача сводится отысанию наименьшео
значения фунции S(x) на промежуте [6; 10]. Единственной
ритичесой точой фунции S(x) является точа x = 5, но она
не принадлежит уазанному промежуту. Следовательно, про-
изводная фунции S(x) не меняет зна на этом промежуте.
Вычислив производную (x) в произвольной точе промежут-
а [6; 10], убеждаемся, что она отрицательна. Ита, наиболь-
шее значение фунции S(x) достиается в левом онце проме-
жута, т. е.
S(x) = S(6) = 48 см
2
.
Рассмотрим теперь второй случай. В этом случае площади
прямоуольниов не превосходят 48 см
2
, та а при одинао-
вой боовой стороне, равной 8 см, длины их оснований не мо-
ут быть больше 6 см.
Ответ.48см
2
.
8. Из всех онусов, вписанных в шар радиуса R, найдите
тот, у отороо площадь боовой поверхности наибольшая.
9. Определите размеры цилиндра, имеющео наибольший
объем, если площадь ео полной поверхности равна 2π.
B
A
C
P
K
LQ
D
Рис. 15
y
10 x–
---------------- -
S
′
max
x Ý [6; 10]

238 Г л а в а 9. Производная и ее применения
10. Среди всех прямоуольных треуольниов площади S
найдите таой, для отороо площадь описанноо руа наи-
меньшая.
11. В полуру радиуса R вписана трапеция ABCD та, что ее
основание AD является диаметром, а вершины B и C лежат на
оружности. Каова величина ула ϕ при основании той трапе-
ции, оторая имеет наибольший периметр?
12. Из всех треуольниов с одинаовым основанием и одним
и тем же улом α при вершине найдите треуольни с наиболь-
шим периметром.
13. В равнобедренный треуольни ABC вписан прямоуоль-
ни, две вершины отороо лежат на основании AB, а две дру-
ие — на сторонах AC и BC. Найдите наибольшее значение пло-
щади прямоуольниа, если AB = 12, BD = 10, де BD — высо-
та треуольниа ABC.
14. Рассматриваются всевозможные трапеции, обе боовые
стороны и меньшее основание оторых равны a. Найдите ве-
личину большео основания трапеции, имеющей наибольшую
площадь.
15. Длина стороны вадрата ABCD равна 10 см. На ео сто-
ронах отложены отрези AA
1
, BB
1
, CC
1
, DD
1
длины x аждый,
причем A
1
Ý AB, B
1
Ý BC, C
1
Ý CD, D
1
Ý DA. Доажите, что
четырехуольни A
1
B
1
C
1
D
1
— вадрат, и найдите значение x,
при отором площадь этоо вадрата наименьшая.
16. В оружность радиуса R вписан равнобедренный тре-
уольни. При аом значении ула α при вершине треуоль-
ниа высота H, проведенная боовой стороне, имеет наиболь-
шую длину? Найдите эту длину.
17. Каим должен быть уол α при вершине равнобедренно-
о треуольниа заданной площади S, чтобы радиус r вписан-
ноо в этот треуольни руа был наибольшим?
В тех случаях, ода тело участвует в двух независимых
движениях, ео путь (или проеция пути на неоторое на-
правление) является фунцией двух или более переменных,
связь между оторыми устанавливается из физичесих сообра-
жений.
18. Туристу требуется попасть на противоположный бере
реи. Под аим улом α ему следует направить лоду, чтобы
добиться наименьшео сноса, если сорость лоди равна v
л
,
а сорость реи равна v
р
?
§ 49. Задачи на отыскание наибольших и наименьших значений 239
19. Тело бросают под улом α оризонту со соростью v
0
.
При аом значении ула α дальность полета тела оажется
наибольшей?
20. Определите наименьшую высоту h = OB двери вертиаль-
ной башни ABCD, чтобы через эту дверь в башню можно было
внести жестий стержень длины l; онец стержня сользит
вдоль оризонтальной прямой, на оторой находится основание
башни AB. Ширина башни AB = d < l.
21. На странице тест должен занимать 384 см
2
. Верхние и
нижние поля должны быть по 3 см, а правое и левое — по 2 см.
Если принять во внимание тольо эономию бумаи, то аовы
должны быть оптимальные размеры страницы?
22. Из рулоо бревна диаметра d требуется вырезать бал-
у прямоуольноо сечения. Каовы должны быть ширина x и
высота y этоо сечения, чтобы бала оазывала наибольшее со-
противление: а) на сжатие; б) на изиб? (Сопротивление бали
на сжатие пропорционально площади ее поперечноо сечения,
а на изиб — произведению ширины этоо сечения на вадрат
ео высоты.)
23. Лампа висит над центром рулоо стола радиуса r. При
аой высоте h лампы над столом освещенность предмета, ле-
жащео на раю стола, будет наилучшей? (Освещенность пря-
мо пропорциональна осинусу ула падения луча света и обрат-
но пропорциональна вадрату расстояния от источниа света.)
24. Требуется устроить прямоуольную площаду та, чтобы
с трех сторон она была оорожена сетой, а четвертой стороной
примыала длинной аменной стене. Каова наивыодней-
шая (в смысле площади) форма площади, если имеется l по-
онных метров сети?
25. На прямолинейном отрезе AB, длина отороо равна a,
соединяющем источнии света A (силой p) и B (силой q), най-
дите точу M, освещаемую слабее всео. (Освещенность обрат-
но пропорциональна вадрату расстояния от источниа света.)
26. Лода находится на расстоянии 3 м от ближайшео
пунта A береа. Пассажир лоди желает достинуть пунта B,
находящеося на береу в 5 м от A. Лода движется со соро-
стью 4 м/ч, а пассажир, выйдя из лоди, может в час пройти
5 м. К аому пунту береа должна прибыть лода, чтобы
пассажир дости пунта B в ратчайшее время?
27. Дождевая апля, начальная масса оторой m
0
, падает под
действием силы тяжести, равномерно испаряясь та, что убыль
массы пропорциональна времени (оэффициент пропорциональ-

238 Г л а в а 9. Производная и ее применения
10. Среди всех прямоуольных треуольниов площади S
найдите таой, для отороо площадь описанноо руа наи-
меньшая.
11. В полуру радиуса R вписана трапеция ABCD та, что ее
основание AD является диаметром, а вершины B и C лежат на
оружности. Каова величина ула ϕ при основании той трапе-
ции, оторая имеет наибольший периметр?
12. Из всех треуольниов с одинаовым основанием и одним
и тем же улом α при вершине найдите треуольни с наиболь-
шим периметром.
13. В равнобедренный треуольни ABC вписан прямоуоль-
ни, две вершины отороо лежат на основании AB, а две дру-
ие — на сторонах AC и BC. Найдите наибольшее значение пло-
щади прямоуольниа, если AB = 12, BD = 10, де BD — высо-
та треуольниа ABC.
14. Рассматриваются всевозможные трапеции, обе боовые
стороны и меньшее основание оторых равны a. Найдите ве-
личину большео основания трапеции, имеющей наибольшую
площадь.
15. Длина стороны вадрата ABCD равна 10 см. На ео сто-
ронах отложены отрези AA
1
, BB
1
, CC
1
, DD
1
длины x аждый,
причем A
1
Ý AB, B
1
Ý BC, C
1
Ý CD, D
1
Ý DA. Доажите, что
четырехуольни A
1
B
1
C
1
D
1
— вадрат, и найдите значение x,
при отором площадь этоо вадрата наименьшая.
16. В оружность радиуса R вписан равнобедренный тре-
уольни. При аом значении ула α при вершине треуоль-
ниа высота H, проведенная боовой стороне, имеет наиболь-
шую длину? Найдите эту длину.
17. Каим должен быть уол α при вершине равнобедренно-
о треуольниа заданной площади S, чтобы радиус r вписан-
ноо в этот треуольни руа был наибольшим?
В тех случаях, ода тело участвует в двух независимых
движениях, ео путь (или проеция пути на неоторое на-
правление) является фунцией двух или более переменных,
связь между оторыми устанавливается из физичесих сообра-
жений.
18. Туристу требуется попасть на противоположный бере
реи. Под аим улом α ему следует направить лоду, чтобы
добиться наименьшео сноса, если сорость лоди равна v
л
,
а сорость реи равна v
р
?
§ 49. Задачи на отыскание наибольших и наименьших значений 239
19. Тело бросают под улом α оризонту со соростью v
0
.
При аом значении ула α дальность полета тела оажется
наибольшей?
20. Определите наименьшую высоту h = OB двери вертиаль-
ной башни ABCD, чтобы через эту дверь в башню можно было
внести жестий стержень длины l; онец стержня сользит
вдоль оризонтальной прямой, на оторой находится основание
башни AB. Ширина башни AB = d < l.
21. На странице тест должен занимать 384 см
2
. Верхние и
нижние поля должны быть по 3 см, а правое и левое — по 2 см.
Если принять во внимание тольо эономию бумаи, то аовы
должны быть оптимальные размеры страницы?
22. Из рулоо бревна диаметра d требуется вырезать бал-
у прямоуольноо сечения. Каовы должны быть ширина x и
высота y этоо сечения, чтобы бала оазывала наибольшее со-
противление: а) на сжатие; б) на изиб? (Сопротивление бали
на сжатие пропорционально площади ее поперечноо сечения,
а на изиб — произведению ширины этоо сечения на вадрат
ео высоты.)
23. Лампа висит над центром рулоо стола радиуса r. При
аой высоте h лампы над столом освещенность предмета, ле-
жащео на раю стола, будет наилучшей? (Освещенность пря-
мо пропорциональна осинусу ула падения луча света и обрат-
но пропорциональна вадрату расстояния от источниа света.)
24. Требуется устроить прямоуольную площаду та, чтобы
с трех сторон она была оорожена сетой, а четвертой стороной
примыала длинной аменной стене. Каова наивыодней-
шая (в смысле площади) форма площади, если имеется l по-
онных метров сети?
25. На прямолинейном отрезе AB, длина отороо равна a,
соединяющем источнии света A (силой p) и B (силой q), най-
дите точу M, освещаемую слабее всео. (Освещенность обрат-
но пропорциональна вадрату расстояния от источниа света.)
26. Лода находится на расстоянии 3 м от ближайшео
пунта A береа. Пассажир лоди желает достинуть пунта B,
находящеося на береу в 5 м от A. Лода движется со соро-
стью 4 м/ч, а пассажир, выйдя из лоди, может в час пройти
5 м. К аому пунту береа должна прибыть лода, чтобы
пассажир дости пунта B в ратчайшее время?
27. Дождевая апля, начальная масса оторой m
0
, падает под
действием силы тяжести, равномерно испаряясь та, что убыль
массы пропорциональна времени (оэффициент пропорциональ-
