Цыпкин А.Г., Пинский А.И. Справочное пособие по математике с методами решения задач для поступающих в вузы
Подождите немного. Документ загружается.


260 Г л а в а 10. Первообразная и интеграл
требуется найти ту, рафи оторой проходит через точу
M(2; 4). Постоянную C найдем из условия
f(2) = · 4 + 2 · 2 + + C = 4 ^ C = –2.
Ответ. F(x) = x
2
+ 2x – 2.
4. Найдите ту первообразную фунции f(x) = x, рафи о-
торой асается прямой y = x – 1.
5. Найдите все первообразные фунции f
1
(x) = x
2
, рафии
оторых асаются параболы f
2
(x) = x
2
+ 1.
6. Найдите все первообразные фунции f(x) = , рафии
оторых асаются ривой y = x
3
.
Если тело движется со соростью, изменяющейся по заону
v = f(t), (5)
то зависимость пути, пройденноо телом, от времени t имеет
вид
s(t) = F(t) + C, (6)
де F(t) — неоторая первообразная фунции f(t), а постоянная
C находится из дополнительных условий.
П р и м е р 3. Тело движется прямолинейно со соростью,
изменяющейся по заону v = 2t м/с. Найти заон движения те-
ла, если известно, что за первые 2 с оно прошло 15 м.
Р е ш е н и е. Множеством всех первообразных фунции
v(t) = 2t является s(t) = t
2
+ C. Соласно условию, имеем
s(2) = 2
2
+ C = 15,
отуда C = 11. Ита, заон движения тела имеет вид s(t) = t
2
+ 11.
Ответ. s(t) = t
2
+ 11.
7. Материальная точа движется прямолинейно со соро-
стью v(t) = sin t cos t м/с. Найдите уравнение движения точи,
если при t = с пройденный путь составляет м.
8. Первый пешеход вышел из пунта A со соростью, изме-
няющейся по заону v(t) = 2t, а второй в тот же момент вышел
из пунта B, отстоящео от A на 4 м, вслед за первым с постоян-
1
2
---
1
2
---
3
x
---
π
3
---
17
8
------
§ 54. Определенный интеграл 261
ной соростью 2p м/ч. При аих значениях p второй пеше-
ход доонит первоо? Найдите значение p, при отором пеше-
ходы поравняются тольо один раз.
§ 54. Определенный интеграл
Определенным интералом на промежуте [a; b] от непре-
рывной фунции f(x) называют приращение F(b) – F(a) любой
первообразной F этой фунции на промежуте [a; b]. Опреде-
ленный интерал обозначают та: f(x)dx. Следовательно,
f(x)dx = F(b) – F(a)(формла Ньютона—Лейбница). (1)
Здесь a и b— нижний и верхний предел интерирования со-
ответственно; f(x) — подынтеральная фунция. Разность
F(b) – F(a), записанная в правой части формулы (1), инода
обозначается F(x).
Для тоо чтобы вычислить определенный интерал от фун-
ции f(x) на промежуте [a; b], необходимо найти любую перво-
образную фунции и вычислить разность ее значений в правом
и левом онцах промежута [a; b].
Правила интерирования
(f(x) + g(x)) dx = f(x)dx + g(x)dx;(2)
kf(x)dx = kf(x)dx; (3)
f(kx + p)dx = f(t)dt, k − 0; (4)
f(x)dx = f(x)dx + f(x)dx, c Ý [a; b]. (5)
a
b
∫
a
b
∫
a
b
a
b
∫
a
b
∫
a
b
∫
a
b
∫
a
b
∫
a
b
∫
1
k
---
ka p+
kb p+
∫
a
b
∫
a
c
∫
c
b
∫

260 Г л а в а 10. Первообразная и интеграл
требуется найти ту, рафи оторой проходит через точу
M(2; 4). Постоянную C найдем из условия
f(2) = · 4 + 2 · 2 + + C = 4 ^ C = –2.
Ответ. F(x) = x
2
+ 2x – 2.
4. Найдите ту первообразную фунции f(x) = x, рафи о-
торой асается прямой y = x – 1.
5. Найдите все первообразные фунции f
1
(x) = x
2
, рафии
оторых асаются параболы f
2
(x) = x
2
+ 1.
6. Найдите все первообразные фунции f(x) = , рафии
оторых асаются ривой y = x
3
.
Если тело движется со соростью, изменяющейся по заону
v = f(t), (5)
то зависимость пути, пройденноо телом, от времени t имеет
вид
s(t) = F(t) + C, (6)
де F(t) — неоторая первообразная фунции f(t), а постоянная
C находится из дополнительных условий.
П р и м е р 3. Тело движется прямолинейно со соростью,
изменяющейся по заону v = 2t м/с. Найти заон движения те-
ла, если известно, что за первые 2 с оно прошло 15 м.
Р е ш е н и е. Множеством всех первообразных фунции
v(t) = 2t является s(t) = t
2
+ C. Соласно условию, имеем
s(2) = 2
2
+ C = 15,
отуда C = 11. Ита, заон движения тела имеет вид s(t) = t
2
+ 11.
Ответ. s(t) = t
2
+ 11.
7. Материальная точа движется прямолинейно со соро-
стью v(t) = sin t cos t м/с. Найдите уравнение движения точи,
если при t = с пройденный путь составляет м.
8. Первый пешеход вышел из пунта A со соростью, изме-
няющейся по заону v(t) = 2t, а второй в тот же момент вышел
из пунта B, отстоящео от A на 4 м, вслед за первым с постоян-
1
2
---
1
2
---
3
x
---
π
3
---
17
8
------
§ 54. Определенный интеграл 261
ной соростью 2p м/ч. При аих значениях p второй пеше-
ход доонит первоо? Найдите значение p, при отором пеше-
ходы поравняются тольо один раз.
§ 54. Определенный интеграл
Определенным интералом на промежуте [a; b] от непре-
рывной фунции f(x) называют приращение F(b) – F(a) любой
первообразной F этой фунции на промежуте [a; b]. Опреде-
ленный интерал обозначают та: f(x)dx. Следовательно,
f(x)dx = F(b) – F(a)(формла Ньютона—Лейбница). (1)
Здесь a и b— нижний и верхний предел интерирования со-
ответственно; f(x) — подынтеральная фунция. Разность
F(b) – F(a), записанная в правой части формулы (1), инода
обозначается F(x).
Для тоо чтобы вычислить определенный интерал от фун-
ции f(x) на промежуте [a; b], необходимо найти любую перво-
образную фунции и вычислить разность ее значений в правом
и левом онцах промежута [a; b].
Правила интерирования
(f(x) + g(x)) dx = f(x)dx + g(x)dx;(2)
kf(x)dx = kf(x)dx; (3)
f(kx + p)dx = f(t)dt, k − 0; (4)
f(x)dx = f(x)dx + f(x)dx, c Ý [a; b]. (5)
a
b
∫
a
b
∫
a
b
a
b
∫
a
b
∫
a
b
∫
a
b
∫
a
b
∫
a
b
∫
1
k
---
ka p+
kb p+
∫
a
b
∫
a
c
∫
c
b
∫
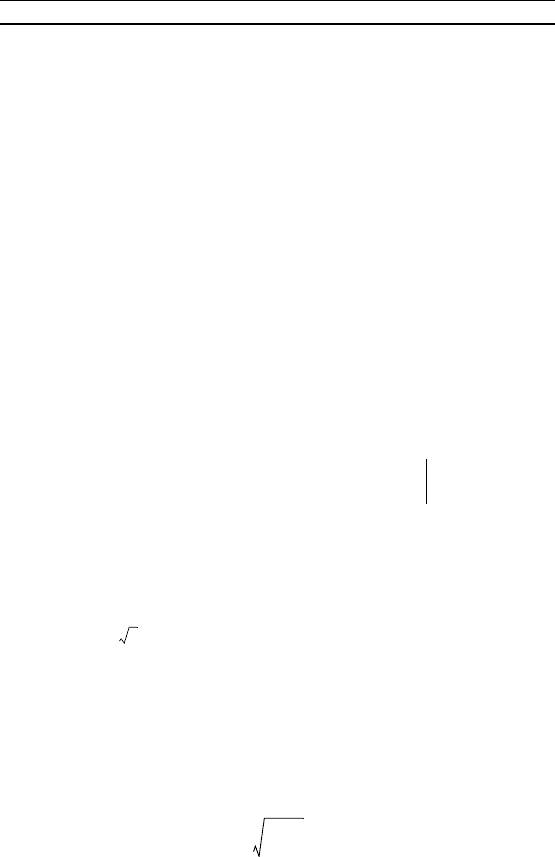
262 Г л а в а 10. Первообразная и интеграл
П р и м е р 1. Вычислить определенный интерал
cos
4
x dx.
Р е ш е н и е. Преобразуем подынтеральную фунцию сле-
дующим образом:
cos
4
x = = (1 + 2 cos 2x + cos
2
2x) =
= 1 + 2 cos 2x + = + cos 2x + cos 4x.
Для фунции cos
4
x первообразной является фунция
F(x) = x + sin 2x + sin 4x.
Вычислим определенный интерал по формуле Ньютона—Лейб-
ница:
cos
4
x dx = x + sin 2x + sin 4x = .
Ответ..
Вычислите интерал:
1. dx. 2. (4x – ) dx.
3. cos x sin x dx. 4. cos x sin 3x dx.
П р и м е р 2. Вычислить интерал
dx.
Р е ш е н и е. Перепишем данный интерал в виде
2 – dx.
0
π/2
∫
1cos2x+
2
--------------------------- -
2
1
4
---
1
4
---
1cos4x+
2
--------------------------- -
3
8
---
1
2
---
1
8
---
3
8
---
1
4
---
1
32
------
0
π/2
∫
3
8
---
1
4
---
1
32
------
0
π/2
3π
16
------ -
3π
16
------ -
1
4
∫
4x 2 x–
x
--------------------------
0,5
1
∫
1
2x
-------
0
π/2
∫
0
π
∫
3
18–
∫
2
x
3
---
–
3
3
18–
∫
x
3
---
1/3
§ 54. Определенный интеграл 263
Воспользуемся формулой (4) при k = – , p = 2; для этоо сна-
чала найдем нижний и верхний пределы интерирования в пра-
вой части этой формулы:
ka + p = – · 3 + 2 = 1, kb + p = (–18) – + 2 = 8.
Далее, полаая 2 – = t, находим – dx = dt, отуда dx = –3 dt.
Теперь, соласно формуле (4), получаем
2 – dx = –3 t
1/3
dt = (–3) = –36 + = –33,75.
Ответ. –33,75.
Вычислите интерал:
5. .
6. .
7. (x – 2) dx. 8. .
9. dx. 10. dx.
11. (sin 2t – cos 2t)
2
dt. 12. .
13. (tg x + ctg x)
–1
dx.
14. 1 – dx.
15. cos
2
– – cos
2
+ dx.
1
3
---
1
3
---
1
3
---
x
3
---
1
3
---
3
18–
∫
x
3
---
1/3
1
8
∫
3t
4/3
4
------------- -
1
8
9
4
---
–8
8
dx
5
x
2
---
+
------------------
–4
2
x dx
2
x
2
---
–
----------------- -
1/3
5/3
∫
3x 1–
1
2
∫
dx
x 1–1x++
-------------------------------------------
2
9
∫
x 1–
3
0
7/3
∫
x 1+
3x 1+
3
---------------------- -
0
π/4
∫
0
1
∫
x dx
x 1+()
2
--------------------- -
π/6
π/4
∫
π/6
π/3
1
1 sin
1–
2x
3π
2
------ -
+
–
----------------------------------------------------
0
π
∫
3π
8
------ -
x
4
---
11π
8
----------
x
4
---
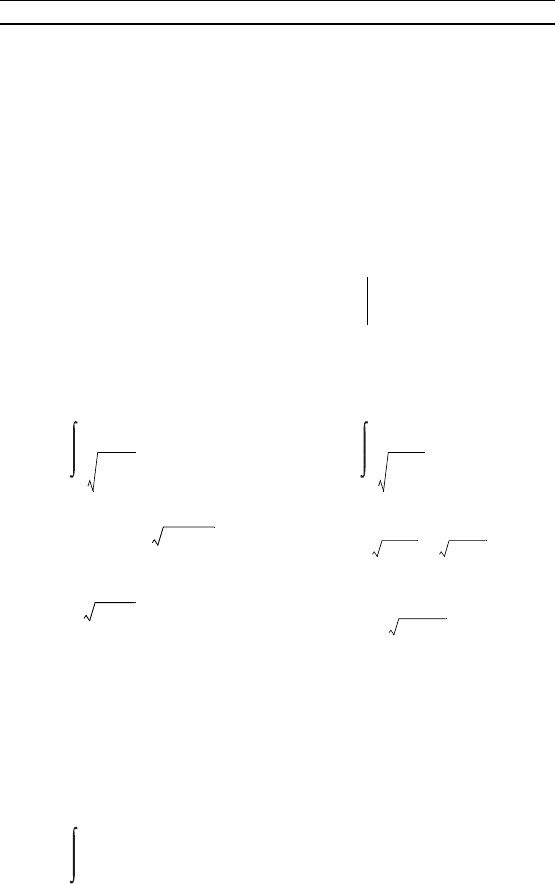
262 Г л а в а 10. Первообразная и интеграл
П р и м е р 1. Вычислить определенный интерал
cos
4
x dx.
Р е ш е н и е. Преобразуем подынтеральную фунцию сле-
дующим образом:
cos
4
x = = (1 + 2 cos 2x + cos
2
2x) =
= 1 + 2 cos 2x + = + cos 2x + cos 4x.
Для фунции cos
4
x первообразной является фунция
F(x) = x + sin 2x + sin 4x.
Вычислим определенный интерал по формуле Ньютона—Лейб-
ница:
cos
4
x dx = x + sin 2x + sin 4x = .
Ответ..
Вычислите интерал:
1. dx. 2. (4x – ) dx.
3. cos x sin x dx. 4. cos x sin 3x dx.
П р и м е р 2. Вычислить интерал
dx.
Р е ш е н и е. Перепишем данный интерал в виде
2 – dx.
0
π/2
∫
1cos2x+
2
--------------------------- -
2
1
4
---
1
4
---
1cos4x+
2
--------------------------- -
3
8
---
1
2
---
1
8
---
3
8
---
1
4
---
1
32
------
0
π/2
∫
3
8
---
1
4
---
1
32
------
0
π/2
3π
16
------ -
3π
16
------ -
1
4
∫
4x 2 x–
x
--------------------------
0,5
1
∫
1
2x
-------
0
π/2
∫
0
π
∫
3
18–
∫
2
x
3
---
–
3
3
18–
∫
x
3
---
1/3
§ 54. Определенный интеграл 263
Воспользуемся формулой (4) при k = – , p = 2; для этоо сна-
чала найдем нижний и верхний пределы интерирования в пра-
вой части этой формулы:
ka + p = – · 3 + 2 = 1, kb + p = (–18) – + 2 = 8.
Далее, полаая 2 – = t, находим – dx = dt, отуда dx = –3 dt.
Теперь, соласно формуле (4), получаем
2 – dx = –3 t
1/3
dt = (–3) = –36 + = –33,75.
Ответ. –33,75.
Вычислите интерал:
5. .
6. .
7. (x – 2) dx. 8. .
9. dx. 10. dx.
11. (sin 2t – cos 2t)
2
dt. 12. .
13. (tg x + ctg x)
–1
dx.
14. 1 – dx.
15. cos
2
– – cos
2
+ dx.
1
3
---
1
3
---
1
3
---
x
3
---
1
3
---
3
18–
∫
x
3
---
1/3
1
8
∫
3t
4/3
4
------------- -
1
8
9
4
---
–8
8
dx
5
x
2
---
+
------------------
–4
2
x dx
2
x
2
---
–
----------------- -
1/3
5/3
∫
3x 1–
1
2
∫
dx
x 1–1x++
-------------------------------------------
2
9
∫
x 1–
3
0
7/3
∫
x 1+
3x 1+
3
---------------------- -
0
π/4
∫
0
1
∫
x dx
x 1+()
2
--------------------- -
π/6
π/4
∫
π/6
π/3
1
1 sin
1–
2x
3π
2
------ -
+
–
----------------------------------------------------
0
π
∫
3π
8
------ -
x
4
---
11π
8
----------
x
4
---
264 Г л а в а 10. Первообразная и интеграл
Если подынтеральная фунция представляет собой выра-
жение, содержащее переменную под знаом модуля, то вычис-
ление определенноо интерала можно свести вычислению
суммы определенных интералов, у оторых подынтеральные
фунции не содержат переменную под знаом модуля.
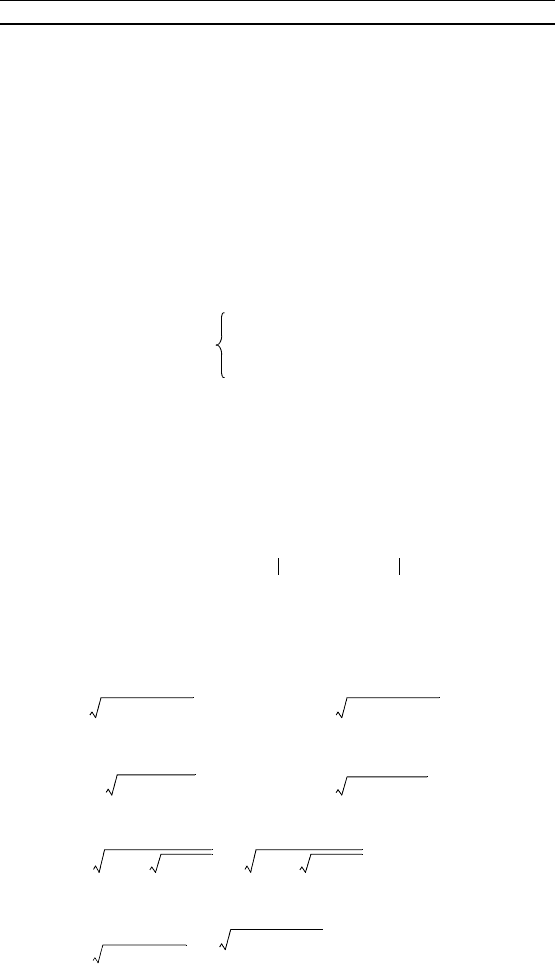
П р и м е р 3. Вычислить интерал
(| x – 3 | + | 1 – x |) dx.
Решение. Представим подынтеральную фунцию в виде
f(x) =
Воспользовавшись свойством (5) определенноо интерала, по-
лучаем
(| x – 3 | + | 1 – x |) dx + (| x – 3 | + | 1 – x |) dx =
= 2 dx + (2x – 4) dx = 2x + (x
2
– 4x) = 4 + 8 = 12.
Ответ.12.
Вычислите интерал:
16. dx. 17. dx.
18. dx. 19. dx.
20. + dx.
21. + dx.
1
5
∫
4 – 2x, x m 1,
2, 1 < x < 3,
2x – 4, x l 3.
1
3
∫
3
5
∫
1
3
∫
3
5
∫
1
3
3
5
1–
1
∫
x
2
2x–1+
0
2
∫
x
2
2x–1+
π/4–
π/2
∫
1cos
2
x–
0
π
∫
1sin2x–
3
5
∫
x 22x 4–+ x 22x 4––
0
3
∫
1
x
2
4x 4++
----------------------------------- -
x
2
4x–4+
§ 55. Интеграл с переменным верхним пределом 265
22. + – 2 dx.
23. dx. 24. dx.
§ 55. Интеграл с переменным
верхним пределом
Интералом с переменным верхним пределом
F(x) = f(t)dt (1)
называют таую первообразную фунции f(x) ( (x) = f(x)),
значение оторой в точе a равно нулю.
П р и м е р 1. Найти наибольшее и наименьшее значения
фунции
F(x) = (t + 1) dt
на промежуте [2; 3].
Р е ш е н и е. Найдем ритичесие точи фунции F(x). Та
а F(x) — первообразная фунции x + 1, то (x) = x + 1;
фунция (x) не обращается в нуль на промежуте [2; 3] и
является положительной. Следовательно, фунция достиает
наибольшео значения на правом онце отреза, а наименьше-
о — на левом:
F(x) = F(3) = (t + 1) dt = + t = 7,5;
F(x) = F(2) = (t + 1) dt = + t = 4.
Ответ. F(x) = 7,5, F(x) = 4.
1/2–
1/2
∫
x 1+
x 1–
------------- -
2
x 1–
x 1+
------------- -
2
1/2
π/2
3π/2
∫
1cos2x–
π/4
3π /2
∫
1cos2x+
a
x
∫
F
′
0
x
∫
F
′
F
′
max
x Ý [2; 3]
0
3
∫
t
2
2
-----
0
3
min
x Ý [2; 3]
0
2
∫
t
2
2
-----
0
2
max
x Ý [2; 3]
min
x Ý [2; 3]

264 Г л а в а 10. Первообразная и интеграл
Если подынтеральная фунция представляет собой выра-
жение, содержащее переменную под знаом модуля, то вычис-
ление определенноо интерала можно свести вычислению
суммы определенных интералов, у оторых подынтеральные
фунции не содержат переменную под знаом модуля.
П р и м е р 3. Вычислить интерал
(| x – 3 | + | 1 – x |) dx.
Решение. Представим подынтеральную фунцию в виде
f(x) =
Воспользовавшись свойством (5) определенноо интерала, по-
лучаем
(| x – 3 | + | 1 – x |) dx + (| x – 3 | + | 1 – x |) dx =
= 2 dx + (2x – 4) dx = 2x + (x
2
– 4x) = 4 + 8 = 12.
Ответ.12.
Вычислите интерал:
16. dx. 17. dx.
18. dx. 19. dx.
20. + dx.
21. + dx.
1
5
∫
4 – 2x, x m 1,
2, 1 < x < 3,
2x – 4, x l 3.
1
3
∫
3
5
∫
1
3
∫
3
5
∫
1
3
3
5
1–
1
∫
x
2
2x–1+
0
2
∫
x
2
2x–1+
π/4–
π/2
∫
1cos
2
x–
0
π
∫
1sin2x–
3
5
∫
x 22x 4–+ x 22x 4––
0
3
∫
1
x
2
4x 4++
----------------------------------- -
x
2
4x–4+
§ 55. Интеграл с переменным верхним пределом 265
22. + – 2 dx.
23. dx. 24. dx.
§ 55. Интеграл с переменным
верхним пределом
Интералом с переменным верхним пределом
F(x) = f(t)dt (1)
называют таую первообразную фунции f(x) ( (x) = f(x)),
значение оторой в точе a равно нулю.
П р и м е р 1. Найти наибольшее и наименьшее значения
фунции
F(x) = (t + 1) dt
на промежуте [2; 3].
Р е ш е н и е. Найдем ритичесие точи фунции F(x). Та
а F(x) — первообразная фунции x + 1, то (x) = x + 1;
фунция (x) не обращается в нуль на промежуте [2; 3] и
является положительной. Следовательно, фунция достиает
наибольшео значения на правом онце отреза, а наименьше-
о — на левом:
F(x) = F(3) = (t + 1) dt = + t = 7,5;
F(x) = F(2) = (t + 1) dt = + t = 4.
Ответ. F(x) = 7,5, F(x) = 4.
1/2–
1/2
∫
x 1+
x 1–
------------- -
2
x 1–
x 1+
------------- -
2
1/2
π/2
3π/2
∫
1cos2x–
π/4
3π /2
∫
1cos2x+
a
x
∫
F
′
0
x
∫
F
′
F
′
max
x Ý [2; 3]
0
3
∫
t
2
2
-----
0
3
min
x Ý [2; 3]
0
2
∫
t
2
2
-----
0
2
max
x Ý [2; 3]
min
x Ý [2; 3]

266 Г л а в а 10. Первообразная и интеграл
Найдите наибольшее и наименьшее значения фунции на
уазанном промежуте:
1. F(x) = sin t dt, x Ý 0; .
2. F(x) = (2t – 5) dt, x Ý [–1; 3].
3. F(x) = (t
2
– 5t + 6) dt, x Ý [0; 4].
4. F(x) = | t |dt, x Ý –; .
5. Запишите уравнения асательных рафиу фунции
F(x) = (2t – 5) dt
в точах ео пересечения с осью абсцисс.
6. Найдите абсциссы точе пересечения рафиов фунций
F
1
(x) = (2t – 5) dt, F
2
(x) = (2t – 5) dt.
7. Найдите точи пересечения рафиов фунций
F
1
(x) = (2t – 5) dt, F
2
(x) = 2t dt.
8. Найдите ту первообразную фунции F(x) = (2t – 5) dt,
рафи оторой проходит через начало оординат.
9. Для рафиа фунции F(x) = 2| t |dt найдите асатель-
ные, параллельные биссетрисе первоо оординатноо ула.
0
x
∫
π
2
---
0
x
∫
0
x
∫
1
x
∫
1
2
---
1
2
---
2
x
∫
2
x
∫
3
x
∫
2
x
∫
0
x
∫
3
x
∫
0
x
∫
§ 55. Интеграл с переменным верхним пределом 267
Пусть тело движется прямолинейно со соростью v(t); A—
неоторая точа на траетории ео движения. Если в момент
времени t = t
0
расстояние между движущимся телом и точой A
равно s
0
, то в любой момент t > t
0
расстояние от движущеося
тела до точи A вычисляется по формуле
s(t) = v(x)dx = s
0
.(2)
П р и м е р 2. Сорость движущеося прямолинейно тела ме-
няется по заону v(t) = + 2t (м/ч). В момент времени t = 1 ч
оно находилось в 5 м от пунта A, расположенноо на трае-
тории движения тела. На аом расстоянии от пунта A оа-
жется тело в момент t = 3 ч?
Р е ш е н и е. Используя соотношения (1) и (2), представим
оординату тела а фунцию времени в виде
s(t) = ( + 2x)dx + 5.
Вычислим значение s(t) при t = 3:
s(3) = ( + 2t)dt + 5 = + t
2
+ 5 =
= 2 + 9 – – 1 + 5 = 12 + 2 .
Ответ. На расстоянии 12 + 2 м от пунта A.
10. Сорость движения тела пропорциональна вадрату вре-
мени. Найдите зависимость между пройденным расстоянием и
временем, если известно, что за первые 3 с тело прошло 18 см,
а движение началось в момент времени t = 0.
11. Сила, действующая на материальное тело, равномерно
меняется относительно пройденноо пути. В начале пути она
была равна 100 Н, а ода тело переместилось на 10 м, сила
возросла до 600 Н. Найдите фунцию, определяющую зависи-
мость работы от пути.
t
0
t
∫
t
1
t
∫
x
1
3
∫
t
2t
3/2
3
------------- -
1
3
3
2
3
---
1
3
---
3
1
3
---
3

266 Г л а в а 10. Первообразная и интеграл
Найдите наибольшее и наименьшее значения фунции на
уазанном промежуте:
1. F(x) = sin t dt, x Ý 0; .
2. F(x) = (2t – 5) dt, x Ý [–1; 3].
3. F(x) = (t
2
– 5t + 6) dt, x Ý [0; 4].
4. F(x) = | t |dt, x Ý –; .
5. Запишите уравнения асательных рафиу фунции
F(x) = (2t – 5) dt
в точах ео пересечения с осью абсцисс.
6. Найдите абсциссы точе пересечения рафиов фунций
F
1
(x) = (2t – 5) dt, F
2
(x) = (2t – 5) dt.
7. Найдите точи пересечения рафиов фунций
F
1
(x) = (2t – 5) dt, F
2
(x) = 2t dt.
8. Найдите ту первообразную фунции F(x) = (2t – 5) dt,
рафи оторой проходит через начало оординат.
9. Для рафиа фунции F(x) = 2| t |dt найдите асатель-
ные, параллельные биссетрисе первоо оординатноо ула.
0
x
∫
π
2
---
0
x
∫
0
x
∫
1
x
∫
1
2
---
1
2
---
2
x
∫
2
x
∫
3
x
∫
2
x
∫
0
x
∫
3
x
∫
0
x
∫
§ 55. Интеграл с переменным верхним пределом 267
Пусть тело движется прямолинейно со соростью v(t); A—
неоторая точа на траетории ео движения. Если в момент
времени t = t
0
расстояние между движущимся телом и точой A
равно s
0
, то в любой момент t > t
0
расстояние от движущеося
тела до точи A вычисляется по формуле
s(t) = v(x)dx = s
0
.(2)
П р и м е р 2. Сорость движущеося прямолинейно тела ме-
няется по заону v(t) = + 2t (м/ч). В момент времени t = 1 ч
оно находилось в 5 м от пунта A, расположенноо на трае-
тории движения тела. На аом расстоянии от пунта A оа-
жется тело в момент t = 3 ч?
Р е ш е н и е. Используя соотношения (1) и (2), представим
оординату тела а фунцию времени в виде
s(t) = ( + 2x)dx + 5.
Вычислим значение s(t) при t = 3:
s(3) = ( + 2t)dt + 5 = + t
2
+ 5 =
= 2 + 9 – – 1 + 5 = 12 + 2 .
Ответ. На расстоянии 12 + 2 м от пунта A.
10. Сорость движения тела пропорциональна вадрату вре-
мени. Найдите зависимость между пройденным расстоянием и
временем, если известно, что за первые 3 с тело прошло 18 см,
а движение началось в момент времени t = 0.
11. Сила, действующая на материальное тело, равномерно
меняется относительно пройденноо пути. В начале пути она
была равна 100 Н, а ода тело переместилось на 10 м, сила
возросла до 600 Н. Найдите фунцию, определяющую зависи-
мость работы от пути.
t
0
t
∫
t
1
t
∫
x
1
3
∫
t
2t
3/2
3
------------- -
1
3
3
2
3
---
1
3
---
3
1
3
---
3

268 Г л а в а 10. Первообразная и интеграл
12. Тело движется равноусоренно, причем известно, что
ео сорость моменту t = 2с достила 4м/с, а пройденный
путь стал равен 3 м. Найдите заон движения тела.
13. При постоянном усорении тело за первую сеунду прео-
долело расстояние 4 м от пунта A, а за первые 3 с расстояние
между ними возросло до 16 м. Найдите зависимость расстоя-
ния, пройденноо телом, от времени, если известно, что при
t = 0 тело находилось в пунте A.
§ 56. Разные задачи, решаемые
с применением свойств интегралов
Решите неравенство:
11. ln – > 0.
12. + dz > x sin
2
x dx.
13. – dz < x cos 2x dx.
14. Найдите таие числа A и B, чтобы фунция
f(x) = A sin πx + B
удовлетворяла условиям (1) = 2, f(x)dx = 4.
5. Найдите все числа a (a > 0), для оторых
(2 – 4x + 3x
2
)dx m a.
6. Найдите все решения уравнения
cos (x + α
2
)dx = sin α,
принадлежащие промежуту [2; 3].
1
3 x–()
3
---------------------
′
6
π
---
0
π
∫
sin
2
x
2
---
dx
x 2+
----------------------------------- -
5x 6– x
2
–
π
2
---
0
x
∫
0
π
∫
x
2
x–12–
0
x
∫
0
π/2
∫
f
′
0
2
∫
0
a
∫
0
α
∫
§ 56. Разные задачи, решаемые с применением свойств интегралов 269
7. Два тела начинают двиаться по прямой одновременно из
одноо и тоо же места в одном направлении. Сорости точе
равны v
1
(t) = 3t
2
м/с, v
2
(t) = 2t м/с. Через сольо сеунд рас-
стояние между телами составит 216 м?
8. Доажите, что любая первообразная нечетной непрерыв-
ной фунции, определенной на промежуте [–a; a], есть фун-
ция четная.
9. Доажите, что четная непрерывная фунция, определен-
ная на промежуте [–a; a], имеет на этом промежуте по рай-
ней мере одну нечетную первообразную.
10. Справедливо ли следующее утверждение: для тоо чтобы
любая первообразная непрерывной фунции f(x) была четной
на промежуте [–a; a], необходимо и достаточно, чтобы фун-
ция f(x) была нечетной на этом промежуте?
11. Найдите значения A, B, C, при оторых фунция
f(x) = Ax
2
+ Bx + C
удовлетворяет условиям
(1) = 8, f(2) + (2) = 33, f(x)dx = .
12. Найдите все значения α из промежута [0; 2π], удовлет-
воряющие уравнению
sin x dx = sin 2α.
13. Найдите положительные значения a, оторые удовлет-
воряют уравнению
(3x
2
+ 4x – 5) dx = a
3
– 2.
14. Найдите все значения α из промежута [–π; 0], удовлет-
воряющие уравнению
sin α + cos 2x dx = 0.
f
′
f
′′
0
1
∫
7
3
---
π/2
α
∫
0
a
∫
α
2α
∫

268 Г л а в а 10. Первообразная и интеграл
12. Тело движется равноусоренно, причем известно, что
ео сорость моменту t = 2с достила 4м/с, а пройденный
путь стал равен 3 м. Найдите заон движения тела.
13. При постоянном усорении тело за первую сеунду прео-
долело расстояние 4 м от пунта A, а за первые 3 с расстояние
между ними возросло до 16 м. Найдите зависимость расстоя-
ния, пройденноо телом, от времени, если известно, что при
t = 0 тело находилось в пунте A.
§ 56. Разные задачи, решаемые
с применением свойств интегралов
Решите неравенство:
11. ln – > 0.
12. + dz > x sin
2
x dx.
13. – dz < x cos 2x dx.
14. Найдите таие числа A и B, чтобы фунция
f(x) = A sin πx + B
удовлетворяла условиям (1) = 2, f(x)dx = 4.
5. Найдите все числа a (a > 0), для оторых
(2 – 4x + 3x
2
)dx m a.
6. Найдите все решения уравнения
cos (x + α
2
)dx = sin α,
принадлежащие промежуту [2; 3].
1
3 x–()
3
---------------------
′
6
π
---
0
π
∫
sin
2
x
2
---
dx
x 2+
----------------------------------- -
5x 6– x
2
–
π
2
---
0
x
∫
0
π
∫
x
2
x–12–
0
x
∫
0
π/2
∫
f
′
0
2
∫
0
a
∫
0
α
∫
§ 56. Разные задачи, решаемые с применением свойств интегралов 269
7. Два тела начинают двиаться по прямой одновременно из
одноо и тоо же места в одном направлении. Сорости точе
равны v
1
(t) = 3t
2
м/с, v
2
(t) = 2t м/с. Через сольо сеунд рас-
стояние между телами составит 216 м?
8. Доажите, что любая первообразная нечетной непрерыв-
ной фунции, определенной на промежуте [–a; a], есть фун-
ция четная.
9. Доажите, что четная непрерывная фунция, определен-
ная на промежуте [–a; a], имеет на этом промежуте по рай-
ней мере одну нечетную первообразную.
10. Справедливо ли следующее утверждение: для тоо чтобы
любая первообразная непрерывной фунции f(x) была четной
на промежуте [–a; a], необходимо и достаточно, чтобы фун-
ция f(x) была нечетной на этом промежуте?
11. Найдите значения A, B, C, при оторых фунция
f(x) = Ax
2
+ Bx + C
удовлетворяет условиям
(1) = 8, f(2) + (2) = 33, f(x)dx = .
12. Найдите все значения α из промежута [0; 2π], удовлет-
воряющие уравнению
sin x dx = sin 2α.
13. Найдите положительные значения a, оторые удовлет-
воряют уравнению
(3x
2
+ 4x – 5) dx = a
3
– 2.
14. Найдите все значения α из промежута [–π; 0], удовлет-
воряющие уравнению
sin α + cos 2x dx = 0.
f
′
f
′′
0
1
∫
7
3
---
π/2
α
∫
0
a
∫
α
2α
∫
