Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

16.7 Subdifferentials and Directional Derivatives 593

To show that f is differentiable, it sufﬁces to show that f(a) + hx, ∇f(a)i approx-

imates f(x) to ﬁrst order near a or, equivalently, that g(x)/kxk tends to 0 as kxk

tends to 0. We use e

, . . . , e

for the standard basis of R

The fact that the n partial derivatives exist means that for 1 ≤ i ≤ n,

0 = lim

h→0

f(a + he

) − f (a) − h

∂f

∂x

(a)

= lim

h→0

f(a + he

) − f (a) − hhe

, ∇f(a)i

= lim

h→0

g(he

)

Fix an ε > 0 and choose r so small that |g(he

)| < ε|h|/n for |h| ≤ r and

1 ≤ i ≤ n.

Take x = (x

, . . . , x

) with kxk ≤ r/n. Then

g(x) = g

i=1

≤

i=1

g(nx

) ≤

i=1

ε|x

| ≤ εkxk.

Now

0 = g(0) = g

x + (−x)

≤

g(x) +

g(−x).

Thus g(x) ≥ −g(−x) ≥ −εkxk. Therefore, |g(x)| ≤ εkxk on B

(0). As ε > 0 is

arbitrary, this proves that f is differentiable at a.

Assuming (2) that f is differentiable at a, the function f(a) + hx, ∇f(a)i ap-

proximates f(x) to ﬁrst order near a with error g(x) satisfying lim

kxk→0

g(x)

kxk

= 0.

Compute

(a;d) = lim

h→0

f(a + hd) − f (a)

= lim

h→0

hhd, ∇f(a)i + g(he

)

= hd, ∇f (a)i+ lim

h→0

g(he

)

= hd, ∇f (a)i.

Theorem 16.7.7 now says that s ∈ ∂f(a) if and only if hd, si ≤



d, ∇f(a)

for all d ∈ R

. Equivalently,



d, s −∇f(a)

≤ 0 for all d ∈ R

. But the left-hand

side takes all real values except when s = ∇f(a). Therefore, ∂f(a) = {∇f(a)}.

Finally, suppose that (3) holds and ∂f (a) = {s}. Then by Corollary 16.7.9,

(a;d) = hd, si. In particular, f

(a;−e

) = −f

(a;e

) and thus

, si = lim

h→0

f(a + he

) − f (a)

= lim

h→0

−

f(a + he

) − f (a)

∂f

∂x

(a).

Hence the partial derivatives of f are deﬁned at a, which proves (1). ¥

594 Convexity and Optimization

16.7.12. EXAMPLE. Let Q be a positive deﬁnite n × n matrix, and let q ∈ R

and c ∈ R. Minimize the quadratic function f(x) = hx, Qxi + hx, qi + c.

We compute the differential

(x;d) = lim

h→0

f(x + hd) − f (x)

= lim

h→0

hx + hd, Q(x + hd)i + hx + hd, qi − hx, Qxi − hx, qi

= lim

h→0

hhd, Qxi + hx, Qhdi + hhd, Qhdi + hhd, qi

= lim

h→0

hd, Qxi + hQx, di + hhd, Qdi + hd, qi = hd, q + 2Qxi.

Thus ∇f(x) = q + 2Qx. We solve ∇f(x) = 0 to obtain the unique minimizer

x = −

−1

q with minimum value f(−

−1

q) = −

hq, Q

−1

qi + c.

This problem can also be solved using linear algebra. The spectral theorem for

Hermitian matrices states that there is an orthonormal basis v

, . . . , v

of eigen-

vectors that diagonalizes Q. Thus there are positive eigenvalues d

, . . . , d

so that

= d

. Write q in this basis as q = q

+ ···+ q

. We also write a generic

vector x as x = x

+ ··· + x

. Then

f(x) = c +

i=1

+ q

= c

i=1

− a

)

where a

= −q

/(2d

) and c

= c −

i=1

Now observe by inspection that the minimum is achieved when x

= a

. To

complete the circle, note that

x =

i=1

= −

i=1

= −

−1

and the minimum value is

f(x) = c

= c −

i=1

= c −

i=1

= c −

hq, Q

−1

qi.

We ﬁnish this section with two of the calculus rules for subgradients. The

proofs are very similar, so we prove the ﬁrst and leave the second as an exercise.

16.7.13. THEOREM. Suppose that f

, . . . , f

are convex functions on R

and

set f (x) = max{f

(x), . . . , f

(x)}. For a ∈ R

, set J(a) = {j : f

(a) = f(a)}.

Then ∂f(a) = conv{∂f

(a) : j ∈ J(a)}.

PROOF. By Theorem 16.6.2, each f

is continuous. Thus there is an ε > 0 so

that f

(x) < f(x) for all kx − ak < ε and all j /∈ J(a). So for x ∈ B

(a),

f(x) = max{f

(x) : j ∈ J(a)}. Fix d ∈ R

and note that f(a + hd) depends only

16.7 Subdifferentials and Directional Derivatives 595

on f

(a + hd) for j ∈ J(a) when |h| < ε/d. Thus using Corollary 16.7.9,

(a;d) = lim

h→0

f(a + hd) − f (a)

= lim

h→0

max

j∈J(a)

(a + hd) − f

(a)

= max

j∈J(a)

(a;d) = max

j∈J(a)

sup{hd, s

i : s

∈ ∂f

(a)}

= sup

hd, si : s ∈ ∪

j∈J(a)

∂f

(a)

= sup

hd, si : s ∈ conv{∂f

(a) : j ∈ J(a)}

This shows that f

(a;·) is the support function of the compact convex set

conv{∂f

(a) : j ∈ J(a)}. However, by Corollary 16.7.9, f

(a;·) is the support

function of ∂f (a). So by the Support Function Lemma (Lemma 16.7.8), these two

sets are equal. ¥

16.7.14. THEOREM. Suppose that f

and f

are convex functions on R

and

and λ

are positive real numbers. Then for a ∈ R

∂(λ

+ λ

)(a) = λ

∂f

(a) + λ

∂f

(a).

Exercises for Section 16.7

A. Show that f

(a;d) is sublinear in d: f

(a;λd + µe) ≤ λf

(a;d) + µf

(a;e) for all

d, e ∈ R

and λ, µ ∈ [0, ∞).

B. Suppose that f is a convex function on a convex subset A ⊂ R

. If a, b ∈ A and

s ∈ ∂f (a), t ∈ ∂f(b), show that hs − t, a − bi ≥ 0.

C. Give an example of a convex set A ⊂ R

, a convex function f on A and a point a ∈ A

such that ∂f(a) is empty.

D. Compute the subdifferential for the norm kxk

∞

= max{|x

|, . . . , |x

|}.

E. Let g be a convex function on R, and deﬁne a function on R

by G(x, y) = g(x) − y.

(a) Compute the directional derivatives of the function G at a point (a, b).

(b) Use Theorem 16.7.7 to evaluate ∂G(a, b). Check you answer against

Example 16.7.4.

F. Prove Theorem 16.7.14—compute ∂f (a) when f = λ

+ λ

as follows:

(a) Show that f

(a;d) = λ

(a;d) + λ

(a;d).

(b) Apply Corollary 16.7.9 to both sides.

∂f

(a) + λ

∂f

(a).

G. Given convex functions f on R

and g on R

, deﬁne h on R

× R

by h(x, y) =

f(x) + g(y). Show that ∂h(x, y) = ∂f(x) × ∂g(y).

HINT: h = F + G, where F (x, y) = f(x) and G(x, y) = g(y).

H. Suppose S is any nonempty subset of R

. We may still deﬁne the support function

of S by σ

= sup{hs, xi : s ∈ S}, but it may sometimes take the value +∞.

(a) If A =

conv(S), show that σ

= σ

(b) Show that σ

is convex.

is ﬁnite valued everywhere if and only if S is bounded.

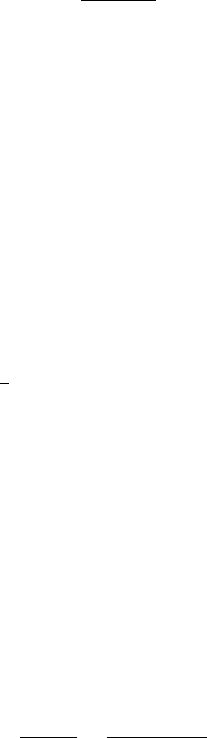
596 Convexity and Optimization

I. Consider a convex function f on a convex set A ⊂ R

and a 6= b ∈ ri(A).

(a) Deﬁne g on [0, 1] by g(λ) = f (λa + (1 − λ)b). If x

= λa + (1 −λ)b, then show

that ∂g(λ) =

hm, b − ai : m ∈ ∂f(x

)

(b) Use the Convex Mean Value Theorem (Exercise 16.5.K) and part (a) to show that

there are λ ∈ (0, 1) and s ∈ ∂f(x

) so that f(b) − f(a) = hs, b − ai.

J. Deﬁne a local subgradient of a convex function f on a convex set A ⊂ R

to be a

vector s so that f(x) ≥ f(a) + hx −a, si for all x ∈ A ∩B

(a) for some r > 0. Show

that if s is a local subgradient, then it is a subgradient in the usual sense.

K. (a) If f

are convex functions on a convex subset A ⊂ R

converging pointwise to f

and s

∈ ∂f

) converge to s, prove that s ∈ ∂f(x

(b) Show that in general, it is not true that every s ∈ ∂f is obtained as such a limit by

considering f

(x) =

+ 1/k on R.

L. Let h = f ¯ g be the inﬁmal convolution of two convex functions f and g on R

(a) Suppose that there are points x

= x

such that h(x

) = f(x

)+g(x

). Prove

that ∂h(x

) = ∂f (x

) ∩ ∂g(x

HINT: s ∈ ∂h(x

) ⇔ f(y) + g(z) ≥ f (x

) + g(x

) + s(y + z −x

). Take y = x

or z = x

(b) If (a) holds and g is differentiable, show that h is differentiable at x

HINT: Theorem 16.7.11

M. Moreau–Yosida. Let f be a convex function on an open convex subset A of R

. For

k ≥ 1, deﬁne f

(x) = f ¯ (kk · k

)(x) = inf

f(y) + kkx − yk

(a) Show that f

≤ f

k+1

≤ f.

(b) Show that x

is a minimizer for f if and only if it is a minimizer for every f

HINT: If f (x

) = f(x

) + ε, ﬁnd r > 0 so that f(x) ≥ f(x

) + ε/2 on B

converges to f.

HINT: If L is a Lipschitz constant on some ball about x

, estimate f

inside and

outside B

√

) separately.

(d) Prove that f

is differentiable for all k ≥ 1.

HINT: Use the previous exercise.

16.8. Tangent and Normal Cones

In this section, we study two special cones associated to a convex subset of R

We develop only a small portion of their theory, since our purpose is to set the stage

for our minimization results, and our results are all related to that speciﬁc goal.

16.8.1. DEFINITION. Consider a convex set A ⊂ R

and a ∈ A. Deﬁne the

cone C

(a) = R

(A − a) generated by A − a. The tangent cone to A at a is the

closed cone T

(a) =

(a) = R

(A − a). The normal cone to A at a is deﬁned

to be N

(a) = {s ∈ R

: hs, x − ai ≤ 0 for all x ∈ A}.

It is routine to verify that T

(a) and N

(a) are closed cones. The cone C

(a)

is only used as a tool for working with T

(a). Notice that hs, x − ai ≤ 0 implies

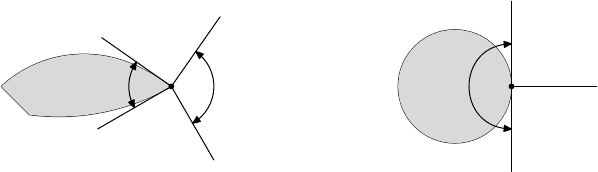
16.8 Tangent and Normal Cones 597

that hs, λ(x − a)i ≤ 0 for all λ > 0. Thus s ∈ N

(a) satisﬁes hs, di ≤ 0 for

all d ∈ C

(a). Since the inner product is continuous, the inequality also holds for

d ∈ T

(a).

a + N

(a)

a + T

(a)

b + N

(b)

b + T

(b)

FIGURE 16.6. Two examples of tangent and normal cones.

16.8.2. EXAMPLE. As a motivating example, let

A = {(x, y) : x ≥ 0, y > 0, x

+ y

< 1} ∪ {(0, 0)} ⊂ R

Then C

((0, 0)) = {(x, y) : x ≥ 0, y > 0} ∪ {(0, 0)}, so the tangent cone is

((0, 0)) = {(x, y) : x, y ≥ 0}. At the boundary points (0, y) for y ∈ (0, 1),

((0, y)) = T

((0, y)) = {(x, y) : x ≥ 0}. Finally, at points (x, y) ∈ int A,

((x, y)) = T

((x, y)) = R

The normal cone gets smaller as the tangent cone increases in size. Here we

have N

((0, 0)) = {(a, b) : a, b ≤ 0}, N

((0, y)) = {(a, 0) : a ≤ 0} for

y ∈ (0, 1) and N

((x, y)) = {0} for (x, y) ∈ int A.

You may ﬁnd it useful to draw pictures like Figure 16.6 for various points in A.

Let us formalize the procedure that produced the normal cone.

16.8.3. DEFINITION. Given a nonempty subset A of R

, the polar cone of A,

denoted A

◦

, is A

◦

= {s ∈ R

: ha, si ≤ 0 for all a ∈ A}.

It is easy to verify that A

◦

is a closed cone. It is evident from the previous

deﬁnition that N

(a) = T

(a)

◦

We need the following consequence of the Separation Theorem.

16.8.4. BIPOLAR THEOREM.

If C is a closed cone in R

, then C

◦◦

= C.

PROOF. From the deﬁnition, C

◦◦

= {d : hd, si ≤ 0 for all s ∈ C

◦

}. This clearly

includes C. Conversely, suppose that x /∈ C. Applying the Separation Theorem

(Theorem 16.3.3), there is a vector s and scalar α so that hc, si ≤ α for all c ∈ C

and hx, si > α. Since C = R

C, the set of values {hc, si : c ∈ C} is a cone

in R. Since C is bounded above by α, it follows that C = R

−

or {0}. Hence

598 Convexity and Optimization

hc, si ≤ 0 ≤ α < hx, si for c ∈ C. Consequently, s belongs to C

◦

. Therefore, x is

not in C

◦◦

. So C

◦◦

= C. ¥

Since N

(a) = T

(a)

◦

, we obtain the following:

16.8.5. COROLLARY. Let A be a convex subset of R

and a ∈ A. Then the

normal and tangent cones at a are polar to each other, namely N

(a) = T

(a)

◦

and T

(a) = N

(a)

◦

16.8.6. EXAMPLE. Let s

, . . . , s

be vectors in R

. Consider the convex poly-

hedron given as A = {x ∈ R

: hx, s

i ≤ r

, 1 ≤ j ≤ m}. What are the tangent

and normal cones at a ∈ A?

Fix a ∈ A. Set J(a) = {j : ha, s

i = r

}. For example, this set is empty if

a ∈ ri(A). Then

(a) =

d = t(x − a) : hx, s

i ≤ r

and some t ≥ 0

d :



+ a, s

≤ r

and some t ≥ 0

d : hd, s

i ≤ t(r

− ha, s

i) and some t ≥ 0

If r

− ha, si > 0, this is no constraint; so C

(a)

d : hd, s

i ≤ 0, j ∈ J(a)

This is closed, and thus T

(a) = C

(a).

Note that {d : hd, si ≤ 0}

◦

= R

s. Indeed, (R

◦

= {d : hd, si ≤ 0}. So

the result follows from the Bipolar Theorem. Now Exercise 16.8.J tells us that

(x) =

j∈J(a)

{d : hd, si ≤ 0}

◦

j∈J(a)

= cone{s

: j ∈ J(a)}.

Indeed, without the exercise, we can see that

cone{s

: j ∈ J(a)}

◦

d : hd, s

i ≤ 0, j ∈ J(a)

= T

(a).

Therefore, by Corollary 16.8.5 and the Bipolar Theorem,

(x) = T

(a)

◦

= cone{s

: j ∈ J(a)}

◦◦

= cone{s

: j ∈ J(a)}.

We need to compute the tangent and normal cones for a convex set A given as

the sublevel set of a convex function.

16.8.7. LEMMA. Let A be a compact convex subset of R

that does not contain

the origin 0. Then the cone R

A is closed.

16.8 Tangent and Normal Cones 599

PROOF. Suppose that a

∈ A and λ

≥ 0 and that c = lim

k→∞

is a point in

A. From the compactness of A, we deduce that there is a subsequence (k

) so

that a

= lim

i→∞

exists in A. Because ka

k 6= 0,

kck

= lim

i→∞

kλ

= lim

i→∞

Therefore, c = lim

i→∞

= λ

belongs to R

A. ¥

16.8.8. THEOREM. Let g be a convex function on R

, and let A be the convex

sublevel set {x : g(x) ≤ 0}. Assume that there is a point x with g(x) < 0. If

a ∈ R

satisﬁes g(a) = 0, then

(a) = {d ∈ R

: g

(a;d) ≤ 0} and N

(a) = R

∂g(a).

PROOF. Let C = {d ∈ R

: g

(a;d) ≤ 0}, which is a closed cone. Suppose that

d ∈ A − a. Then [a, a + d] is contained in A and thus g(a + hd) − g(a) ≤ 0 for

0 < h ≤ 1. So g

(a;d) ≤ 0 and hence d ∈ C. As C is a closed cone, it follows

that C contains R

(A − a) = T

(a).

Choose x ∈ A with g(x) < 0, and set d = x − a. Then

(a;d) = inf

h>0

g(a + hd) − g(a)

≤

g(a + d) − g(a)

< 0.

Hence by Lemma 16.6.5, intC = {d : g

(a;d) < 0} is nonempty and moreover

C = intC.

Let d ∈ intC. Since g

(a;d) < 0, there is some h > 0 so that g(a + hd) < 0.

Consequently, a + hd belongs to A and d ∈ R

(A − a) ⊂ T

(a). So intC is a

subset of T

(a). Thus C = intC is contained in T

(a), and the two cones agree.

By Corollary 16.7.9, g

(a;d) = sup{hd, si : s ∈ ∂g(a)}. Thus d ∈ T

(a)

if and only if hd, si ≤ 0 for all s ∈ ∂g(a), which by deﬁnition is the polar cone

of ∂g(a). Hence by the Bipolar Theorem (Theorem 16.8.4), the polar N

(a) of

(a) is the closed cone generated by ∂g(a). Note that 0 /∈ ∂g(a) because a is not

a minimizer of g (Proposition 16.7.2). Therefore, by Lemma 16.8.7, N

(a) is just

∂g(a). ¥

Exercises for Section 16.8

A. Show that T

(a) and N

(a) are closed convex cones.

B. For a point v ∈ R

, show that v ∈ N

(a) if and only if P

(a + v) = a.

C. If C is a closed cone, show that T

(0) = C and N

(0) = C

◦

D. Suppose that A ⊂ R

is convex and f is a convex function on A. Prove that x

∈ A is

a minimizer for f in A if and only if f

, d) ≥ 0 for all d ∈ T

600 Convexity and Optimization

E. Let f (x, y) = (x − y

)(x − 2y

). Show that (0, 0) is not a minimizer of f on R

yet

((0, 0), d) ≥ 0 for all d ∈ R

. Why does this not contradict the previous exercise?

F. If C

⊂ C

, show that C

◦

⊂ C

◦

G. If A is a subspace of R

, show that A

◦

is the orthogonal complement of A.

H. Suppose that a

, . . . , a

are vectors in R

. Compute conv({a

, . . . , a

})

◦

I. If A is a convex subset of R

, show that A

◦

= {0} if and only if 0 ∈ int(A).

HINT: Use the Separation Theorem and Support Theorem.

J. Suppose that C

and C

are closed cones in R

(a) Show that (C

+ C

)

◦

= C

◦

∩ C

◦

(b) Show that (C

∩ C

)

◦

+ C

◦

HINT: Use the Bipolar Theorem and part (a).

K. Given a convex function f on R

, deﬁne g on R

n+1

by g(x, r) = f(x) − r and

A = epi(f) = {(x, r) : f(x) ≤ r}. Use Theorem 16.8.8 to verify

(a) T

(x, f(x))

= {(d, p) : f

(x;d) ≤ p},

(b) intT

(x, f(x))

= {(d, p) : f

(x;d) < p}, and

(x, f(x))

= R

[∂f (x) × {−1}].

(d) For n = 1, explain the last equation geometrically.

L. For a convex subset A ⊂ R

, show that the following are equivalent for x ∈ A:

(1) x ∈ ri(A).

(2) T

(x) is a subspace.

(3) N

(x) is a subspace.

(4) y ∈ N

(x) implies that −y ∈ N

(x).

M. (a) Suppose C ⊂ R

is a closed convex cone and x /∈ C. Show that y ∈ C is the

closest vector to x if and only if x − y ∈ C

◦

and hy, x − yi = 0.

HINT: Recall Theorem 16.3.1. Expand kx − yk

(b) Hence deduce that x = P

(x) + P

◦

N. Give an example of two closed cones in R

whose sum is not closed.

HINT: Let C

= cone{(x, y, 1) : (x, y) ∈ A

}, where A

and A

come from Exer-

cise 16.2.G(c).

O. A polyhedral cone in R

is a setAR

= {Ax : x ∈ R

}for somematrix A mapping

into R

. Show that (AR

)

◦

= {y ∈ R

: A

y ≤ 0}, where A

is the transpose

of A and z ≤ 0 means z

≤ 0 for 1 ≤ i ≤ m.

P. Suppose A ⊂ R

and B ⊂ R

are convex sets. If (a, b) ∈ A × B, then show that

A×B

(a, b) = T

(a) × T

(b) and N

A×B

(a, b) = N

(a) × N

(b).

Q. Suppose that A

and A

are convex sets and a ∈ A

∩ A

(a) Show that T

∩A

(a) ⊂ T

(a) ∩ T

(a).

(b) Give an example where this inclusion is proper.

HINT: Find a convex set A in R

such that the positive y-axis Y

is contained in

(0) but A ∩ Y

= {(0, 0)}.

16.9 Constrained Minimization 601

16.9. Constrained Minimization

The goal of this section is to characterize the minimizers of a convex function

subject to constraints that limit the domain of the function to a convex set. Gen-

erally, this convex set is not explicitly described but is given as the intersection of

level sets. That is, we are only interested in minimizers in some speciﬁed convex

set. The ﬁrst theorem characterizes such minimizers abstractly, using the normal

cone of the constraint set and the subdifferentials of the function. If the constraint

is given as the intersection of sublevel sets of convex functions, these conditions

may be described explicitly in terms of subgradients analogous to the Lagrange

multiplier conditions of multivariable calculus. Finally, we present another charac-

terization in terms of saddlepoints.

We will only consider convex functions that are deﬁned on all of R

, rather than

a convex subset. This is not as restrictive as it might seem. Exercise 16.9.H will

guide you through a proof that any convex function satisfying a Lipschitz condition

on a convex set A extends to a convex function on all of R

. There are convex

functions that cannot be extended. For example, f(x) = −

√

x − x

on [0, 1] is

convex, but cannot be extended to all of R because the derivative blows up at 0 and

We begin with the problem of minimizing a convex function f deﬁned on R

over a convex subset A. A point x in A is called a feasible point.

16.9.1. THEOREM. Suppose that A ⊂ R

is convex and that f is a convex

function on R

. Then the following are equivalent for a ∈ A:

(1) a is a minimizer for f|

(2) f

(x;d) ≥ 0 for all d ∈ T

(a).

(3) 0 ∈ ∂f (a) + N

(a).

PROOF. First assume (3) that 0 ∈ ∂f(a) + N

(a); so there is a vector s ∈ ∂f(a)

such that −s ∈ N

(a). Recall that N

(a) = {v : hx − a, vi ≤ 0 for all x ∈ A}.

Hence hx − a, si ≥ 0 for x ∈ A. Now use the fact that s ∈ ∂f(a) to obtain

f(x) ≥ f(a) + hx − a, si ≥ f (a).

Therefore, a is a minimizer for f on A. So (3) implies (1).

Assume (1) that a is a minimizer for f on A. Let x ∈ A and set d = x − a.

Then [a, x] = {a + hd : 0 ≤ h ≤ 1} is contained in A. So f(a + hd) ≥ f (a) for

h ∈ [0, 1] and thus

(a;d) = lim

h→0

f(a + hd) − f (a)

≥ 0.

Because f

(a;·) is positively homogeneous and is nonnegative on A −a, it follows

that f

(a;d) ≥ 0 for d in the cone R

(A − a). But f

(a;·) is deﬁned on all of R

and hence is continuous by Theorem 16.6.2. Therefore, f

(a;·) ≥ 0 on the closure

(a) =

(A − a). This establishes (2).

602 Convexity and Optimization

By Theorem 16.7.3, since a is in the interior of R

, the subdifferential ∂f(a)

is a nonempty compact convex set. Thus the sum ∂f(a) + N

(a) is closed and

convex by Exercise 16.2.G. Suppose that (3) fails: 0 /∈ ∂f (a) + N

(a). Then we

may apply the Separation Theorem 16.3.3 to produce a vector d and scalar α so

that

sup{hs + n, di : s ∈ ∂f(a), n ∈ N

(a)} ≤ α < h0, di = 0.

It must be the case that hn, di ≤ 0 for n ∈ N

(a), for if hn, di > 0, then

hs + λn, di = hs, di + λhn, di > 0

for very large λ. Therefore, d belongs to N

(a)

◦

= T

(a) by Corollary 16.8.5.

Now take n = 0 and apply Corollary 16.7.9 to compute

(a;d) = sup{hs, di : s ∈ ∂f(a)} ≤ α < 0.

Thus (2) fails. Contrapositively, (2) implies (3). ¥

Theorem 16.9.1 is a fundamental and very useful result. In particular, condi-

tion (3) does not depend on where a is in the set A. For example, if a is an interior

point of A, then N

(a) = {0} and this theorem reduces to Proposition 16.7.2.

Given that all we know about the constraint set is that it is convex, this theorem is

the best we can do. However, when the constraints are described in other terms,

such as the sublevel sets of convex functions, then we can ﬁnd more detailed char-

acterizations of the optimal solutions.

16.9.2. DEFINITION. By a convex program, we mean the ingredients of a

minimization problem involving convex functions. Precisely, we have a convex

function f on R

to be minimized. The set over which f is to be minimized is

not given explicitly but instead is determined by constraint conditions of the form

(x) ≤ 0, where g

, . . . , g

are convex functions. The associated problem is

Minimize f(x)

subject to constraints g

(x) ≤ 0, . . . , g

(x) ≤ 0.

We call a ∈ R

a feasible vector for the convex program if a satisﬁes the con-

straints, that is, g

(a) ≤ 0 for i = 1, . . . , r. A solution a ∈ R

of this problem is

called an optimal solution for the convex program, and f(a) is the optimal value.

The set over which f is minimized is the convex set A =

1≤i≤r

{x : g

(x) ≤ 0}.

The r functional constraints may be combined to obtain A = {x : g(x) ≤ 0},

where g(x) = max{g

(x) : 1 ≤ i ≤ r}. The function g is also convex. This is

useful for technical reasons, but in practice the conditions g

may be superior (for

example, they may be differentiable). It is better to be able to express optimality

conditions in terms of the g

themselves.

In order to solve this problem, we need to impose some sort of regularity con-

dition on the constraints that allows us to use our results about sublevel sets.