Davidson K.R., Donsig A.P. Real Analysis with Real Applications

Подождите немного. Документ загружается.

16.9 Constrained Minimization 603

16.9.3. DEFINITION. A convex program satisﬁes Slater’s condition if there is

point x ∈ R

so that g

(x) < 0 for i = 1, . . . , r. Such a point is called a strictly

feasible point or a Slater point.

16.9.4. KARUSH–KUHN–TUCKER THEOREM.

Consider a convex program that satisﬁes Slater’s condition. Then a ∈ R

is an

optimal solution if and only if there is a vector w = (w

, . . . , w

) ∈ R

with

≥ 0 for 1 ≤ j ≤ r so that

0 ∈ ∂f (a) + w

∂g

(a) + ··· + w

∂g

(a),

(a) ≤ 0, w

(a) = 0 for 1 ≤ j ≤ r.

(KKT)

The relations (KKT) are called the Karush-Kuhn-Tucker conditions. If a is

an optimal solution, the set of vectors w ∈ R

that satisfy (KKT) are called the

(Lagrange) multipliers.

A slight variant on these conditions for differentiable functions was given in

a 1951 paper by Kuhn and Tucker and was labeled with their names. Years later,

it came to light that they also appeared in Karush’s unpublished Master’s thesis of

1939, and so Karush’s name was added.

This deﬁnition of multipliers appears to depend on which optimal point a

is used. However, the set of multipliers is in fact independent of a; see Exer-

cise 16.9.E.

PROOF. We introduce the function g(x) = max{g

(x) : 1 ≤ i ≤ r} as mentioned

previously. Then the feasible set becomes

A = {x ∈ R

: g

(x) ≤ 0, 1 ≤ i ≤ r} = {x ∈ R

: g(x) ≤ 0}.

Slater’s condition guarantees that the set {x : g(x) < 0} is nonempty. Hence by

Lemma 16.6.5, this is the interior of A.

Assume that a ∈ A is an optimal solution. In particular, a is feasible, so

(a) ≤ 0 for all j. By Theorem 16.9.1, 0 ∈ ∂f (a)+N

(a). When a is an interior

point, then N

(a) = {0} and so 0 ∈ ∂f(a). Set w

= 0 for 1 ≤ j ≤ r and the

conditions (KKT) are satisﬁed. Otherwise we may suppose that g(a) = 0.

The hypotheses of Theorem 16.8.8 are satisﬁed, and so N

(a) = R

∂g(a).

When the subdifferential of g is computed using Theorem 16.7.13, it is found to be

∂g(a) = conv{∂g

(a) : j ∈ J(a)}, where J(a) = {j : g

(a) = 0}. We claim that

(a) =

j∈J(a)

: w

≥ 0, s

∈ ∂g

(a)

Indeed, every element of ∂g(a) has this form, and multiplication by a positivescalar

preserves it. Conversely, if w =

j∈J(a)

6= 0, then

j∈J(a)

belongs to

conv{∂g

(a) : j ∈ J(a)}, and so

j∈J(a)

belongs to R

∂g(a).

Therefore, the condition 0 ∈ ∂f(a) + N

(a) may be restated as s ∈ ∂f(a),

∈ ∂g

(a), w

≥ 0 for j ∈ J(a) and s +

j∈J(a)

= 0. By deﬁnition,

(a) = g(a) = 0 for j ∈ J(a), whence we have w

(a) = 0. For all other j, we

set w

= 0 and (KKT) is satisﬁed.

604 Convexity and Optimization

Conversely suppose that (KKT) holds. Since g

(a) ≤ 0, a is a feasible point.

The conditions w

(a) = 0 mean that w

= 0 for j /∈ J(a). If a is strictly feasible,

J(a) is the empty set. In this event, (KKT) reduces to 0 ∈ ∂f(a) = ∂f(a)+N

(a).

On the other hand, when g(a) = 0, we saw that in this instance the (KKT) condition

is equivalent to 0 ∈ ∂f(a) + N

(a). In both cases, Theorem 16.9.1 implies that a

is an optimal solution. ¥

Notice that if f and each g

is differentiable, then ﬁrst part of (KKT) becomes

0 = ∇f (a) + w

∇g

(a) + ··· + w

∇g

(a),

which is more commonly written as a system of linear equations

0 =

∂f

∂x

(a) + w

∂g

∂x

(a) + ··· + w

∂g

∂x

(a) for 1 ≤ i ≤ n.

This is known as a Lagrange multiplier problem. So we adopt the same terminology

here.

These conditions can be used to solve concrete optimization problems in much

the same way as in multivariable calculus. Their greatest value for applications

is in understanding minimization problems, which can lead to the development of

efﬁcient numerical algorithms.

16.9.5. DEFINITION. Given a convex program, deﬁne the Lagrangian of this

system to be the function L on R

× R

given by

L(x, y) = f(x) + y

(x) + ··· + y

(x).

Next, we recall the deﬁnition of a saddlepoint from multivariable calculus.

There are several equivalent conditions for saddlepoints given in the Exercises.

16.9.6. DEFINITION. Suppose that X and Y are sets and L is a real-valued

function on X × Y . A point (x

, y

) ∈ X × Y is a saddlepoint for L if

L(x

, y) ≤ L(x

, y

) ≤ L(x, y

) for all x ∈ X, y ∈ Y.

We shall be interested in saddlepoints of the Lagrangian over the set R

×R

We restrict the y variables to the positive orthant R

because the (KKT) conditions

require nonnegative multipliers.

16.9.7. THEOREM. Consider a convex program that admits an optimal solution

and satisﬁes Slater’s condition. Then a is an optimal solution and w a multiplier

for the program if and only if (a, w) is a saddlepoint for its Lagrangian function

L(x, y) = f (x) + y

(x) + ···y

(x) on R

× R

. The value L(a, w) at any

saddlepoint equals the optimal value of the program.

16.9 Constrained Minimization 605

PROOF. First suppose that L(a, y) ≤ L(a, w) for all y ∈ R

. Observe that

j=1

− w

(a) = L(a, y) − L(a, w) ≤ 0.

Since each y

may be taken to be arbitrarily large, this forces g

(a) ≤ 0 for each

j. So a is a feasible point. Also, taking y

= 0 and y

= w

for i 6= j yields

−w

(a) ≤ 0. Since this quantity is positive, we deduce that w

(a) = 0. So

L(a, w) = f(a) +

(a) = f (a).

Now turn to the condition L(a, w) ≤ L(x, w) for all x ∈ R

. This means

that h(x) = L(x, w) = f(x) +

(x) has a global minimum at a. By

Proposition 16.7.2, 0 ∈ ∂h(a). We may compute ∂h(a) using Theorem 16.7.14.

So 0 ∈ ∂f(a) +

j=1

∂g

(a). This establishes the (KKT) conditions, and thus a

is a minimizer for the convex program and w is a multiplier.

Conversely, suppose that a and w satisfy (KKT). Then g

(a) ≤ 0 because a is

feasible and w

(a) = 0 for 1 ≤ j ≤ r. So w

= 0 except for j ∈ J(a). Thus

L(a, y) −L(a, w) =

j /∈J(a)

(a) ≤ 0. The other part of (KKT) states that the

function h(x) has 0 ∈ ∂h(a). Thus by Proposition 16.7.2, a is a minimizer for h.

That is, L(a, w) ≤ L(x, w) for all x ∈ R

. So L has a saddlepoint at (a, w). ¥

If we had a multiplier w for the convex program, then to solve the convex

program it is enough to solve the unconstrained minimization problem:

inf{L(x, w) : x ∈ R

This shows one important property of multipliers: They turn constrained optimiza-

tion problems into unconstrained ones. In order to use multipliers in this way, we

need a method for ﬁnding multipliers without ﬁrst solving the convex program.

This problem is addressed in the next section.

16.9.8. EXAMPLE. Consider the following example. Let g be a convex function

on R and ﬁx two points p = (x

, y

) and q = (x

, y

) in R

. Minimize the sum

of the distances to p and q over A = epi(g) = {(x, y) : G(x, y) ≤ 0}, where

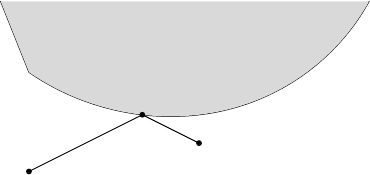
G(x, y) = g(x) − y, as indicated in Figure 16.7.

epi(g)

FIGURE 16.7. Minimizing the sum of two distances.

606 Convexity and Optimization

Then the function of v = (x, y) ∈ R

to be minimized is

f(v) = kv−pk + kv−qk =

(x−x

)

+ (y−y

)

(x−x

)

+ (y−y

)

Using Example 16.7.10, we may compute that

∂f(v) =











(0) +

p−q

kp−qk

if v = p

(0) −

p−q

kp−qk

if v = q

v−p

kv−pk

v−q

kv−qk

if x 6= p, q.

Note that 0 ∈ ∂f (v) if v = p or q or the two vectors v − p and v − q point in

opposite directions, namely v ∈ [p, q]. This is obvious geometrically.

To make the problem more interesting, let us assume that A does not intersect

the line segment [p, q]. The (KKT) conditions at the point v = (x, y) become

g(x) ≤ y w ≥ 0 w(g(x) − y) = 0

0 ∈ ∂f (v) + w∂G(v).

The ﬁrst line reduces to saying that v = (x, g(x)) lies in the boundary of A and

w ≥ 0. Alternatively, we could observe that N

(v) = {0} when v ∈ intA, and

thus 0 /∈ ∂f(v) + N

(v), whence the minimum occurs on the boundary.

At a point x, we know that ∂g(x) = [D

−

g(x), D

g(x)]. Thus by Exam-

ple 16.7.4 for v = (x, g(x)),

∂G(v) =

(s, −1) : s ∈ [D

−

g(x), D

g(x)]

So by Theorem 16.8.8, N

(v) =

(st, −t) : s ∈ [D

−

g(x), D

g(x)], t ≥ 0

Thus the second statement of (KKT) says that the sum of the two unit vectors in the

directions p − v and q − v is an element of N

(v). Now geometrically this means

that p −v and q −v make the same angle on opposite sides of some normal vector.

In particular, if g is differentiable at v, then N

(v) = R

(x), −1) is the

outward normal to the tangent line at v. So the geometric condition is just that

the angles to the tangent (from opposite sides) made by [p, v] and [q, v] are equal.

In physics, this is the well-known law: The angle of incidence equals the angle of

reﬂection. This fact for a light beam reﬂecting off a surface is explained by Fermat’s

Principle that a beam of light will follow the fastest path (hence the shortest path)

between two points.

However, this criterion works just as well when g is not differentiable. For

example, take g(x) = |x| and points p = (−1, −1) and q = (2, 0). Then

∂g(x) =











−1 if x < 0

[−1, 1] if x = 0

+1 if x > 0.

We will verify the (KKT) condition at the point 0 = (0, 0). First observe that

∂G(0) = [−1, 1] × {−1}. So

(0) = R

∂g(0) × {−1}

= {(s, t) : t ≤ 0}

16.9 Constrained Minimization 607

consists of the lower half-plane. Now

∂f(0) = (1, 1)/

√

2 + (−2, 0)/2 = (

√

− 1,

√

)

lies in the upper half-plane. In particular,

√

− 1,

√

1 −

√

2, −1) = (0, 0).

So w = 1/

√

2 and v = (0, 0) satisfy (KKT), and thus (0, 0) is the minimizer.

Exercises for Section 16.9

A. Minimize x

+ y

− 4x − 6y subject to x ≥ 0, y ≥ 0, and x

+ y

≤ 4.

B. Minimize ax + by subject to x ≥ 1 and

√

xy ≥ K. Here a, b, and K are positive

constants.

C. Minimize

subject to x + y + z = 1 and x, y, z > 0.

HINT: Find the Lagrange multipliers.

D. Suppose (x

, y

) and (x

, y

) are saddlepoints of a real valued function p on X × Y .

(a) Show that (x

, y

) and (x

, y

) are also saddlepoints.

(b) Show that p takes the same value at all four points.

E. (a) Use the previous exercise to show that the set of multipliers for a convex program

do not depend on the choice of optimal point.

(b) Show that the set of multipliers is a closed convex subset of R

A × M, where A is the set of optimal solutions and M is the set of multipliers.

F. Given a real-valued function p on X × Y , deﬁne functions α on X and β on Y by

α(x) = sup{p(x, y) : y ∈ Y } and β(y) = inf{p(x, y) : x ∈ X}. Show that for

, y

) ∈ X × Y the following are equivalent:

(1) (x

, y

) is a saddlepoint for p.

(2) p(x

, y) ≤ p(x, y

) for all x ∈ X and all y ∈ Y .

(3) α(x

) = p(x

, y

) = β(y

(4) α(x

) ≤ β(y

G. Let g be a convex function on R and let p = (x

, y

) ∈ R

. Find a criterion for the

closest point to p in A = epi(g).

(a) What is the function f to be minimized? Find ∂f(v).

(b) What is the constraint function G? Compute ∂G(v).

(d) Simplify these conditions and interpret them geometrically.

H. Suppose that A is an open convex subset of R

and f is a convex function on A that is

Lipschitz with constant L. Construct a convex function g on R

extending f:

(a) Show if a ∈ A and v ∈ ∂f(a), then kvk ≤ L.

HINT: Check the proof of Theorem 16.7.3.

(b) For x ∈ R

and a, b ∈ A and s ∈ ∂f(a), show that

f(b) + Lkx − bk ≥ f (a) + hs, x − ai.

608 Convexity and Optimization

by g(x) = inf{f (a) + Lkx −ak : a ∈ A}. Show that g(x) > −∞

for x ∈ R

and that g(a) = f(a) for a ∈ A.

(d) Show that g is convex.

I. Let f and g

, . . . , g

be C

functions on R

. The problem is to minimize f over the

set A = {x : g

(x) ≤ 0, 1 ≤ j ≤ m}. Let J(x) = {j : g

(x) = 0}. Prove that a

feasible point x

is a local minimum if and only if there are constants λ

not all 0 so

that λ

∇f(x

) +

j∈J(x

)

∇g

) = 0.

HINT: Let g(x) = max{f(x) − f(x

), g

(x) : j ∈ J(x

)}. Compute ∂g(x

) by

Theorem 16.7.13. Use Exercise 16.3.J to deduce g

;d) ≥ 0 for all d if and only if

0 ∈ cone{∇f(x

), ∇g

) : j ∈ J(x

)}.

J. Dufﬁn’s duality gap. Let b ≥ 0, and consider the convex program:

Minimize f(x, y) = e

−y

subject to g(x, y) =

+ y

− x ≤ b in R

(a) Find the feasible region. For which b is Slater’s condition satisﬁed?

(b) Solve the problem. When is the minimum attained?

K. An alternativeapproach to solving minimization problems is to eliminate the constraint

set g

(x) ≤ 0 and instead modify f by adding a term h(g

(x)), where h is an increasing

function with h(y) = 0 for y ≤ 0. The quantity h(g

(x)) is a called a penalty, and this

approach is the penalty method. Assume that f and each g

are continuous functions

on R

but not necessarily convex. Let h

(y) = k(max{y, 0})

. For each integer

k ≥ 1, we have the minimization problem: Minimize F

(x) = f(x) +

i=1

(x))

for x ∈ R

. Suppose that this minimization problem has a solution a

and the original

has a solution a.

(a) Show that F

) ≤ F

k+1

) ≤ f(a).

(b) Show that lim

k→∞

i=1

)) = 0.

is the limit of a subsequence of (a

), show that it is a minimizer.

(d) If f(x) → ∞ as kxk → ∞, deduce that the minimization problem has a solution.

16.10. The Minimax Theorem

In addition to the Lagrangian of the previous section, saddlepoints play a cen-

tral role in various other optimization problems. For example, they arise in game

theory and mathematical economics. Our purpose in this section is to examine the

mathematics that leads to the existence of a saddlepoint under quite general hy-

potheses. Examination of a typical saddlepoint in R

shows that the cross sections

in the xz-plane are convex functions while the cross sections in the yz-plane are

concave. See Figure 16.8. It is this trade-off that gives the saddle its characteristic

shape. Hence we make the following deﬁnition:

16.10.1. DEFINITION. A function p(x, y) deﬁned on X ×Y is called convex–

concave if p(·, y) is a convex function of x for each ﬁxed y ∈ Y and p(x, ·) is a

concave function of y for each ﬁxed x ∈ X.

16.10 The Minimax Theorem 609

FIGURE 16.8. A typical saddlepoint.

The term minimax comes from comparing two interesting quantities:

∗

= sup

y∈Y

inf

x∈X

p(x, y) and p

∗

= inf

x∈X

sup

y∈Y

p(x, y),

which are the maximin and minimax, respectively. These quantities make sense

for any function p. Moreover, for x

∈ X and y

∈ Y ,

inf

x∈X

p(x, y

) ≤ p(x

, y

) ≤ sup

y∈Y

p(x

, y).

Take the supremum of the left-hand side over y

∈ Y to get p

∗

≤ sup

y∈Y

p(x

, y),

since the right-hand side does not depend on y

. Then take the inﬁmum over all

∈ X to obtain p

∗

≤ p

∗

Suppose that there is a saddlepoint ( ¯x, ¯y), that is, p( ¯x, y) ≤ p( ¯x, ¯y) ≤ p(x, ¯y)

for all x ∈ X and y ∈ Y . Then

∗

≥ inf

x∈X

p(x, ¯y) ≥ p( ¯x, ¯y) ≥ sup

y∈Y

p( ¯x, y) ≥ p

∗

Thus the existence of a saddlepoint shows that p

∗

= p

∗

We will use the following variant of Exercise 16.6.J.

16.10.2. LEMMA. Let f

, . . . , f

be convex functions on a convex subset X of

. For c ∈ R, the following are equivalent:

(1) There is no point x ∈ X satisfying f

(x) < c for 1 ≤ j ≤ r.

(2) There exist λ

≥ 0 so that

= 1 and

≥ c on X.

PROOF. If (1) is false and f

) < c for 1 ≤ j ≤ k, then

) < c for all

choices of λ

≥ 0 with

= 1. Hence (2) is also false.

Conversely, assume that (1) is true. Deﬁne

Y = {y ∈ R

: y

> f

(x) for 1 ≤ j ≤ r and some x ∈ X}.

This set is open and convex (left as Exercise 16.10.B). By hypothesis, the point

z = (c, c . . . , c) ∈ R

is not in Y . Depending on whether z belongs to

Y or not,

we apply either the Support Theorem (Theorem 16.3.7) or the Separation Theorem

610 Convexity and Optimization

(Theorem 16.3.3) to obtain a hyperplane that separates z from Y . That is, there is a

nonzero vector h = (h

, . . . , h

) in R

and α ∈ R so that hy, hi < α ≤ hz, hi for

all y ∈ Y .

We claim that each coefﬁcient h

≤ 0. Indeed, for any x ∈ X, Y contains

(x), . . . , f

(x)

+ te

for any t ≥ 0, where e

is a standard basis vector for R

Thus

j=1

(x) + th

≤ α, which implies that h

≤ 0.

Deﬁne λ

= h

/H, where H =

j=1

< 0. Then λ

≥ 0 and

= 1.

Restating the separation for

(x), . . . , f

(x)

∈ Y , we obtain

j=1

(x) ≥

≥

hz, hi

j=1

cλ

= c.

So (2) holds. ¥

Now we establish our saddlepoint result. First we assume compactness. We

will remove it later, at the price of adding a mild additional requirement.

16.10.3. MINIMAX THEOREM (COMPACT CASE).

Let X be a compact convex subset of R

and let Y be a compact convex subset of

. If p is a convex–concave function on X × Y , then p has a nonempty compact

convex set of saddlepoints.

PROOF. For each y ∈ Y , deﬁne a convex function on X by p

(x) = p(x, y). For

each c > p

∗

, deﬁne A

y,c

= {x ∈ X : p

(x) ≤ c}. Then this is a nonempty

compact convex subset of X.

For any ﬁnite set of points y

, . . . , y

in Y , we claim that A

∩ ··· ∩ A

is nonempty. If not, then there is no point x so that p

(x) < c for 1 ≤ j ≤ r.

So by Lemma 16.10.2, there would be scalars λ

≥ 0 with

= 1 so that

≥ c on X. Set ˜y =

i=1

. As p is concave in y,

c ≤

i=1

p(x, y

) ≤ p(x, ˜y) for all x ∈ X.

Consequently, c ≤ min

x∈X

p(x, ¯y) ≤ p

∗

, which is a contradiction.

Let {y

: i ≥ 1} be a dense subset of Y , and set c

= p

∗

+ 1/n. Then the

set A

i=1

is nonempty closed and convex. It is clear that A

contains

n+1

, and thus this is a decreasing sequence of compact sets in R

. By Cantor’s In-

tersection Theorem (Theorem 4.4.7), the set A =

n≥1

is a nonempty compact

set. (It is also convex, as the reader can easily verify.)

Let ¯x ∈ A. Then ¯x ∈ A

for all n ≥ 1. Thus p( ¯x, y

) ≤ c

for all i ≥ 1 and

n ≥ 1. So p(¯x, y

) ≤ p

∗

. But the set {y

: i ≥ 1} is dense in Y and p is continuous,

so p( ¯x, y) ≤ p

∗

for all y ∈ Y . Therefore,

∗

= inf

x∈X

max

y∈Y

p(x, y) ≤ max

y∈Y

p( ¯x, y) ≤ p

∗

16.10 The Minimax Theorem 611

Since p

∗

≤ p

∗

is always true, we obtain equality. Choose a point ¯y ∈ Y so that

p( ¯x, ¯y) = p

∗

. Then p( ¯x, y) ≤ p( ¯x, ¯y) ≤ p(x, ¯y) for all x ∈ X and y ∈ Y . That is,

( ¯x, ¯y) is a saddlepoint for p.

By Exercise 16.9.D, the set of saddlepoints is a rectangle A × B. Moreover,

the same argument required in Exercise 16.9.E shows that this rectangle is closed

and convex. ¥

Slippery things can happen at inﬁnity if precautions are not taken. However,

the requirements of the next theorem are often satisﬁed.

16.10.4. MINIMAX THEOREM.

Suppose that X is a closed convex subset of R

and Y is a closed convex subset of

. Assume that p is convex–concave on X ×Y , and in addition assume that

(1) if X is unbounded, then there is a y

∈ Y so that p(x, y

) → +∞ as

kxk → ∞ for x ∈ X.

(2) if Y is unbounded, then there is an x

∈ X so that p(x

, y) → −∞ as

kyk → ∞ for y ∈ Y .

Then p has a nonempty compact convex set of saddlepoints.

PROOF. We deal only with the case in which both X and Y are unbounded. The

reader can ﬁnd a modiﬁcation that works when only one is unbounded.

By the hypotheses, max

y∈Y

p(x

, y) = α < ∞ and min

x∈X

p(x, y

) = β > −∞.

Clearly, β ≤ p(x

, y

) ≤ α. Set

= {x ∈ X : p(x, y

) ≤ α + 1} and Y

= {y ∈ Y : p(x

, y) ≥ β + 1}.

Conditions (1) and (2) guarantee that X

and Y

are bounded, and thus they are

compact and convex. Let A × B be the set of saddlepoints for the restriction of p

to X

× Y

provided by the compact case.

In particular, let ( ¯x, ¯y) be one saddlepoint, and let c = p( ¯x, ¯y) be the critical

value. Then

β ≤ p( ¯x, y

) ≤ p( ¯x, ¯y) = c ≤ p(x

, ¯y) ≤ α.

Let x ∈ X \ X

, so that p(x, y

) > α + 1. Now p(·, y

) is continuous, and

hence there is a point x

in [x, ¯x] with p(x

, y

) = α + 1. So x

∈ X

and x

6= ¯x.

Thus x

= λx + (1 −λ) ¯x for some 0 < λ < 1. As p(·, ¯y) is convex,

c ≤ p(x

, ¯y) ≤ λp(x, ¯y) + (1 −λ)p( ¯x, ¯y) = λp( ¯x, ¯y) + (1 −λ)c.

Hence p( ¯x, ¯y) = c ≤ p(x, ¯y). Similarly, for every y ∈ Y \ Y

, we may show that

p( ¯x, y) ≤ c = p( ¯x, ¯y). Therefore, ( ¯x, ¯y) is a saddlepoint in X × Y . ¥

Now let us see how this applies to the problem of constrained optimization.

Consider the convex programming problem: Minimize a convex function f(x) over

the closed convex set X = {x : g

(x) ≤ 0, 1 ≤ j ≤ r}. Suppose that it satisﬁes

Slater’s condition. The Lagrangian L(x, y) = f(x) + y

(x) + ···+ y

(x) is a

convex function of x for each ﬁxed y ∈ R

, and is a linear function of y for each

x ∈ R

. So, in particular, L is convex–concave on R

× R

612 Convexity and Optimization

Now we also suppose that this problem has an optimal solution. Then we can

apply Theorem 16.9.7 and the Karush–Kuhn–Tucker Theorem (Theorem 16.9.4) to

guarantee a saddlepoint (a, w) for L; and L(a, w) is the solution of the convex pro-

gram. By the argumentsof this section, it follows that the existence of a saddlepoint

means that the optimal value is also obtained as the maximin:

f(a) = min

x∈X

f(x) = L

∗

= max

y∈R

inf

x∈R

L(x, y).

Deﬁne h(y) = inf

x∈R

f(x) + y

(x) + ···y

(x) for y ∈ R

. While its deﬁni-

tion requires an inﬁmum, h gives a new optimization problem, which can be easier

to solve. This new problem is called the dual program:

Maximize h(y) over y ∈ R

16.10.5. PROPOSITION. Consider a convex program that admits an optimal

solution and satisﬁes Slater’s condition. The solutions of the dual program are

exactly the multipliers of the original program, and the optimal value of the dual

program is the same.

PROOF. Suppose a is an optimal solution of the original program and w a multi-

plier. Then L(a, y) ≤ L(a, w) ≤ L(x, w) for all x ∈ R

and y ∈ R

since (a, w)

is a saddlepoint for the Lagrangian L. In particular,

h(w) = inf{L(x, w) : x ∈ R

} = L(a, w).

Moreover, for any y ∈ R

with y 6= w, h(y) ≤ L(a, y) ≤ L(a, w) = h(w). So w

is a solution of the dual problem, and the value is L(a, w) = L

∗

, which equals the

value of the original problem.

Conversely, suppose that w

is a solution of the dual program. Let (a, w) be a

saddlepoint. Then

∗

= L(a, w) ≥ L(a, w

) ≥ h(w

) = L

∗

Thus h(w

) = L(a, w

) = L

∗

. Therefore, L(a, w

) = h(w

) ≤ L(x, w

) for all

x ∈ R

. Also, since (a, w) is a saddlepoint, L(a, y) ≤ L(a, w) = L(a, w

) for all

y ∈ R

. Consequently, w

is a multiplier. ¥

An important fact for computational purposes is that since these two problems

have the same answer, we can obtain estimates for the solution by sampling. Sup-

pose that we have a point x

∈ X and y

∈ R

so that h(y

) − f(x

) < ε. Then

since we know that the solution lies in [f(x

), h(y

)], we have a good estimate for

the solution even if we cannot compute it exactly.

16.10.6. EXAMPLE. Consider a quadratic programming problem. Let Q be

a positive deﬁnite n ×n matrix, and let q ∈ R

. Also let A be an m ×n matrix and

a ∈ R

. Minimize the quadratic function f(x) = hx, Qxi+ hx, qi over the region

Ax ≤ a.

We can assert before doing any calculation that this minimum will be attained.

This follows from the global version, Example 16.7.12, where it was shown that