Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

402 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

It is nice to have such a quantitative computational expression for the radius of the sphere

through four points in such a coordinate-free form. In structural exercise 1, you derive a

similar direct expression for the center of the sphere.

The computation we have just done was in 3-D space, which is why we needed to use

four elements to span the sphere. Apart from that, nothing in the computation depended

on the dimensionality. If we move into a plane, exactly the same construction can be

used to show that three unit points p ∧ q ∧ r span a circle, of which the radius squared is

proportional to (p ∧ q ∧ r)

. (If you are uncomfortable about whether this might be true

in a general offset plane, just move the plane so that it contains the origin, perform the

construction, and move it back to where it came from. The structure preservation of the

versors then makes the result move with the motion and be valid in the offset plane as

well.) Summarizing:

oriented sphere through points p, q, r, s: p ∧ q ∧ r ∧ s

oriented circle through points p, q, r: p ∧ q ∧ r

oriented point pair through points p, q: p ∧ q

We emphasize that a directed point pair is a single element of conformal geometric algebra,

just one 2-blade B. There is therefore no need to make a separate data structure for an

edge, because the point pair contains all information. So in contrast to the homogeneous

model, we can have a line segment as a single element of computation. It is even possible

to retrieve the constituent points from the 2-blade B (see (14.13) in structural exercise 4).

That is of course not possible for the other blades representing rounds; many triples of

points determine the same circle.

As you play with such elements p ∧q ∧r ∧s in an interactive software package with visual-

ization, it is pleasing to see how the independence of the result on motions of the points

over the sphere is captured by the antisymmetry of the outer product. Switching on some

display of the orientation of the sphere (as captured by the sign of its weight), you should

see that orientation change in continuous and predictable manner, depending on whether

p, q, r, s form a positively oriented tetrahedron or not. Can you determine the geometri-

cal relationship between p, q, r, and s that makes the sphere become zero (see structural

exercise 3)?

14.1.3 ORIENTED ROUNDS

We have seen above that a dual circle κ can be characterized as the dual meet σ ∧ π of a

sphere σ and a plane π through the sphere’s center (so that the two are perpendicular and

σ · π = 0). This was a geometrical construction, and we were not too particular about

the signs involved. But you normally want to use the capability of geometric algebra to

represent oriented spheres, circles, and point pairs, so we should be more speciﬁc. The

orientation of the direct circle K in direct representation is most easily characterized as

the orientation of its carrier plane K∧∞; proper dualization then gives the form we should

use for the dual representation to get the desired matching orientation.

SECTION 14.1 ROUNDS 403

To avoid having to ﬁx signs later, we work from a direct form with obviously correct

orientation (though with a somewhat mysterious spherical part) to determine the correct

dual. We claim that the direct form of a round at the origin is

Σ=(o +

∞) A

, (14.6)

with A

purely Euclidean. The carrier ﬂat of this round is Π=Σ∧∞= o ∧ A

∧∞, with

the orientation of A

. We compute the corresponding dual:

∗



(o +

∞) A



(o ∧ I

−1

∧∞)





(o +

∞)



(o ∧∞∧



−1

)







(o −

∞) ∧



−1



= (o −

∞)(A





−1

)

= (o −

∞) A

夹

(−1)

(14.7)

This shows both the correctness of the direct representation of the round (since it pro-

duces a dual of the correct form), and how we should choose the sign of the dual to repre-

sent a round with a particular orientation. You should really use this instead of the earlier

expression (14.2), which was unspeciﬁc on the orientation.

For instance, to dually represent a circle with unit radius rotating positively (counter-

clockwise) in the e

∧ e

-plane, we have A

= e

∧ e

. In 3-D space with the regular

pseudoscalar, the dual circle is (o −

∞)(−e

); in a 4-D space, the dual circle would be

(o −

∞)(−e

∧ e

Collectively, we call these elements derived from the intersection of a sphere with planes

direct rounds, a term that includes oriented spheres, oriented circles, and oriented point

pairs in 3-D, but clearly extends to any dimension. The above shows its representation

to be

direct real round at origin: Σ=(o +

∞) A

. (14.8)

Note the difference with the dual round representation of (14.1): for a real direct round,

a factor appears that looks like an imaginary dual sphere. Direct imaginary rounds are of

the form (o −

∞) A

, simply changing the sign on ρ

To correspond to mathematical tradition, we can call a round a (k−1)-sphere if its carrier

has dimension k. The mathematical indication of dimensionality refers to the dimension

of the manifold of its shell. What we call a sphere in 3-D is a 2-D curved surface, and there-

fore called a 2-sphere; we could call it a 2-round. A circle is a 1-D manifold and therefore

a 1-sphere. A point pair is a 0-sphere; it is unique in having two separate components.

By translation using a rotor T

, we can produce general rounds around any point c,asthe

elements

direct round: (c +

∞) ∧



− c(



∞)



, (14.9)

404 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

where we used the translation formula (13.7). A k-sphere is therefore represented by a

(k + 2)-blade. The associated dual round with the same orientation is

dual round: (c −

∞) ∧



− c(



夹

∞)



, (14.10)

whichisan(n − k)-blade. (To obtain (14.10), we applied (13.7) to (14.7), and canceled

some signs.) These expressions have been collected in Table 14.1 for easy reference, though

more compactly denoted through translation rotors applied to standard forms around the

origin.

14.2 TANGENTS AS INTERSECTIONS OF

TOUCHING ROUNDS

In the representation of a round the radius can be set to zero. This results in a blade that

squares to zero. To ﬁnd its geometric interpretation, let us construct a setup in which it

naturally occurs. We put two (dual) spheres with equal radius ρ at opposite sides of the

origin, in the unit e

-direction, as depicted in Figure 14.2. You can easily verify that these

spheres are represented by the vectors o ± e

(1 − ρ

) ∞. We compute the dual meet

by the outer product of the duals and simplify the outcome:



o − e

(1 − ρ

)∞



∧



o + e

(1 − ρ

)∞





o −

(ρ

− 1)∞



∧ (2e

) (14.11)

There are three cases:

•

When ρ

> 1 (as in Figure 14.2(a)) we get a real dual circle, nicely factored in the

outer product as the intersection of a real dual sphere (with squared radius ρ

− 1)

and the dual plane 2e

that denotes the ﬂat carrier plane of the circle.

•

Butwhenwehaveρ

< 1 (as in Figure 14.2(c)), the resulting intersection circle

becomes imaginary and is factored as the intersection of a plane and an imaginary

sphere (with the squared radius ρ

− 1 now being negative).

•

When ρ

= 1, we get Figure 14.2(b). Geometrically, we would say that the spheres

now have a tangent 2-blade in common. You can think of this tangent 2-blade as

the intersection point of the two spheres with a tiny bit of plane attached. We have

sketched it like that in Figure 14.2(b). This is apparently represented by the dual

blade o ∧ (2e

It is interesting that we obtain this kind of inﬁnitesimal element through application of the

incidence operator, not by any differentiation or limiting process, and that we therefore

have them available as regular blades of the conformal model. The only unusual thing

about them is that they square to zero.

Let us study this class of blade in its direct form, at the origin. We can make it by setting the

radius of a direct round to zero, producing from (14.8) the element o∧A

as the standard

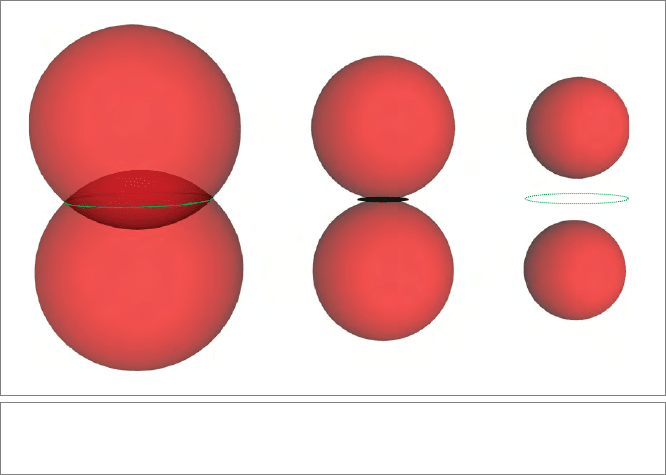
SECTION 14.2 TANGENTS AS INTERSECTIONS OF TOUCHING ROUNDS 405

Figure 14.2: Intersection of two spheres of decreasing radii, leading to (a) a real circle, (b) a

tangent 2-blade, and (c) an imaginary circle.

form at the origin. For k = 2, a tangent 2-blade results. These are new elements; we shall

call them (direct) tangents.

direct tangent at origin: o ∧ A

They have a location (here o) and a direction, but they are not ﬂats (since they lack the

element ∞). A direct ﬂat can be constructed from such an element by making it pass

through inﬁnity, as (o ∧ A

) ∧∞; this shows clearly that A

is the directional element of

the tangent.

If A

isavectorA

= a, this tangent element looks like o ∧ a.Thismaybepicturedasa

vector in direction a located at the origin. We can ﬁnd out which point set it represents

by solving x ∧ (o ∧ a) = 0, and this yields that only x = o is in it, but clearly o ∧a is more

than just o; it also has a directional part a. It can be made as the

meet of two circles (see

structural exercise 7). Note that a tangent vector is not a small vector: the signed length of

a vector is given by its weight, and that can be arbitrarily big. It is the size of the tangent

vector element that is zero, as its zero square shows; you can interpret it as a pair of very

close points, if that helps. The sharp distinction between size and weight occurs for the

ﬁrst time in the conformal model, which therefore appears as the natural framework to

represent elements that are small in their 2-point geometric size, yet have a ﬁnite weight.

These are ﬁnite elements of geometry, not inﬁnitesimals!

406 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

The dual representation of the tangent is of course obtained from the representation of

the dual round of (14.10), setting its radius to zero, giving

dual tangent at origin: o ∧ A

夹

(−1)

As with the rounds, this involves a sign to relate the orientation to that of the direct repre-

sentation. Apart from that, you see that the dualization is the Euclidean dual: the tangents

embed the vector space model into the conformal model, one copy at each location. In math-

ematics, this is called the tangent bundle; the conformal model gives us its elements as

regular elements of computation.

Displacing a direct tangent element using a translation rotor, it becomes

direct tangent: p ∧ ( −p(



∞)).

Note that you should not simply use p ∧ A

as the translated element!

A tangent X is a blade characterized by having zero square (X

= 0), since it is like a round

with zero radius. But it does not contain ∞ (so that ∞∧X = 0). A dual tangent X

∗

satisﬁes

the dual of these conditions: (X

∗

)

= 0, while ∞X

∗

= 0. Because of these conditions, it

is consistent to view a point as a special case of a tangent element, with a scalar directional

part denoting its weight: p ∧ α. In that view, a point is a localized scalar.

14.2.1 EUCLID’S ELEMENTS

We have now found all elements of Euclidean geometry as encoded in the conformal

model. The basic objects are represented by the blades assembled in Table 14.1.

Note in the table that, apart from the ﬂats, the elements retain their appearance after dual-

ization: a dual direction may be confused with a directly represented direction, a tangent

with a dual tangent, and a real dual round with an imaginary direct round, all of com-

plimentary Euclidean properties of direction and/or size. Since we cannot tell them apart

from their structure alone, we need to specify somehow whether they are intended for

direct or dual usage.

This is a bit of a nuisance; we might have hoped that direct and dual representations

had been more clearly separated in the conformal model. But at least direct and dual

elements transform in precisely the same manner under even versors, so keeping track of

their nature is only required for interpretation, not for correct algebraic manipulation.

That in itself is an improvement over the homogeneous model in which direct and dual

representations translate differently.

SECTION 14.2 TANGENTS AS INTERSECTIONS OF TOUCHING ROUNDS 407

Table14.1: All nonzero blades in the conformal model of Euclidean geometry and their parameters. Locations are denoted

by dual spheres. The normalized points q are probes to give locations closest to q; one may just use q = o. The direc-

tions are computed in direct form, although the dualized version is also given. The weight in all cases is computed as



|qdirection(X)|

, orientation is relative to the chosen pseudoscalar for the directional subspace.

As for notation,



X = (−1)

grade(X)

X is the grade involution, E

夹

is a Euclidean dual, X

−∗

is the undualization in the full space. T

denotes a translation to the position p relative to the origin, to signify the general form of the elements.

Standard Form X Condition Direction E ∞ Location Squared Size

direction ∞∧X = 0

E∞ ∞X = 0 X none none

dual direction ∞∧X = 0

−E

夹

∞ ∞X = 0 X

−∗

none none

ﬂat ∞∧X = 0

[o ∧ (E∞)] ∞X = 0 −∞X (qX)/X none

dual ﬂat ∞∧X = 0

[



夹

] ∞X = 0 −∞X

−∗

(q ∧ X)/X none

tangent ∞∧X = 0

[o E] ∞X = 0 −(∞X) ∧∞

−∞X

= 0

dual tangent ∞∧X = 0

[o E

夹

(−1)

] ∞X = 0 (−∞X

−∗

) ∧∞

−∞X

= 0

round ∞∧X = 0

−∞X

[(o +

∞) E] ∞X = 0 −(∞X) ∧∞ ρ



(∞X)

= 0 or −

X∞X

(∞X)

dual round ∞∧X = 0

−∞X

[(o −

∞) E

夹

(−1)

] ∞X = 0 ( −∞X

−∗

) ∧∞ ρ

= −



(∞X)

= 0 or −

X∞X

(∞X)

408 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

14.2.2 FROM BLADES TO PARAMETERS

So far, we have constructed the elements from parameters such as centers, radii, and direc-

tions. But we also need the reverse process to ﬁnd out what kind of element a computation

has produced, so we need to be able to classify a given blade and retrieve its parameters.

For this task, the intimidating Table 14.1 is intended as reference.

Computing these geometric parameters of the various kinds of blades is not too hard, and

the various formulas are easily proved (or derived when you have forgotten them) from

a blade in its standard form around the origin. This is allowed as long as all formulas

are Euclidean covariant (i.e., they don’t use position or orientation-dependent construc-

tions). You know from Section 13.2 that a good way to guarantee that is to write them

using only the standard products, and only ∞ as a special element (since the point at

inﬁnity is a Euclidean invariant).

We give the algebraic formulas for size, weight, location, and direction. In an implementa-

tion, you can often just read off these elements as the coefﬁcients of speciﬁc components of

the blade normalized by the overall weight (which may be found as another coefﬁcient)—

as long as you do not use different coordinate systems within a single application.

•

Squared Size. The square of a normalized dual sphere gives you its radius squared,

for

(o −

∞ρ

)

= −

(o ∞ + ∞o) ρ

= ρ

For a dual round in general, you need to do a normalization and mind some grade-

dependent signs. An unnormalized dual round X has

= (o −

∞) E

夹

(o −

∞) E

夹

= ρ

夹



夹

Since ∞X = E

夹

(−1)

, the squared size can now be computed by normalization

and by a grade inversion to compensate for the extra sign in the Euclidean part. This

gives



(∞X)

For the direct representation of a round, the structure is similar. Therefore, the total

formulas are as indicated in Table 14.1. It is good custom to denote the squared size

rather than the size itself, since the square may be negative and we want to avoid

introducing complex numbers.

All tangents and dual tangents have size 0. For the ﬂats and directions, size is not an

issue, since they do not have any (they only have a weight).

•

Direction, Weight, and Orientation. A ﬂat or round is in a translated linear sub-

space with a certain direction. This direction can be retrieved from the element by

a speciﬁc formula for each category of element. The formulas are easily derived,

they merely strip off the positional parts (if any) and supply a ∞-factor (if lacking).

SECTION 14.3 TANGENTS AS INTERSECTIONS OF TOUCHING ROUNDS 409

All return a direction of the form E∧∞, with E purely Euclidean, and may be found

in Table 14.1.

The Euclidean parts of these directions may not be of unit weight or positive ori-

entation relative to the pseudoscalar of the Euclidean subspace they belong to.

In that case, the magnitude of the direction is the weight of the element, and its

sign the orientation. The orientation is somewhat arbitrary, since it must be relative

to the orientation of the pseudoscalar, which is a matter of choice or convention.

The weight of an element of the form E ∞ can be computed by stripping off the ∞

(through a contraction with o or any other normalized point q), and computing the

weight of the Euclidean part. That gives



|qdirection(X)|



|q(E∞)|

Since all elements have a direction, all elements have a weight and orientation. In

some cases, these weights have a traditional way being displayed: a vector of weight

2 can be depicted as having length 2, and a tangent bivector of weight 2 as an area

element of 2 area units. But a sphere of weight 2 is not a sphere of radius 2; rather it

should be visualized as a heavier or denser spherical shell.

•

Location. The location of a blade should be the Euclidean coordinates of some rel-

evant point. For a round, this is naturally the center, but for ﬂats such as lines and

planes such a point is not uniquely indicated in a coordinate-free manner.

For ﬂats, we can either take the point of it that is closest to the origin (obviously not

coordinate-free) or the point that is closest to some given point q. The formulas in

the table actually produce a normalized dual sphere σ as the location (rather than a

point, i.e., a dual sphere of radius zero), since that is a simple formula. This is often

sufﬁcient in intermediate computations, but you can take its Euclidean part as the

Euclidean location vector (easy in most coordinate-based implementations, though

algebraically it is (o ∧∞)(o ∧∞∧σ)).

For the rounds, we only need to strip off the carrier part to be left with a dual sphere

around the center, and this is done by computing X/(−∞X). Alternatively, we may

compute the normalized center point directly as a dual sphere of radius zero through

c = −

X ∞X

(∞X)

For now, just accept this formula. We will appreciate this properly as computing

the reﬂection of ∞ in the normalized round when we treat the operators of the

conformal model in Chapter 16.

The result of these considerations is Table 14.1, which computes all parameters of the

elements of all classes.

410 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

14.3 A VISUAL EXPLANATION OF ROUNDS

AS BLADES

The vector space model and the homogeneous model may have accustomed us to think-

ing of the blades in a representation space as always representing ﬂat elements in the base

space. Algebraically, this interpretation appears to be supported by the idea that they must

represent subspaces and therefore be linear. However, this argument confuses the repre-

sentational space with the base space that is being represented. We can show you more

visually why the surprising characterization of Euclidean rounds by blades works, to con-

vince you of its intuitive correctness. In this section we will “pop up” the ∞-dimension

graphically, though we will necessarily show you only the conformal model for a 2-D

Euclidean geometry

14.3.1 POINT REPRESENTATION

We have seen that a Euclidean point at the location x is represented as the conformal

vector

x = o + x +

∞.

In 2-D Euclidean space

, this requires a 4-D representational space R

3,1

with a basis

like {o, e

, e

, ∞}. This would seem to be hard to visualize. However, the o-dimension

works very much like the extra dimension in homogeneous coordinates: it allows us to

represent offset linear subspaces (i.e., linear subspaces that are shifted out of the origin in

a representational space with basis {e

, e

, ∞}). So because of the o-term, we are allowed

to draw conformal planes, lines, and so on, that do not need to go through the origin.

If you accept that, we do not need to draw this dimension explicitly. We just use this

freedom and know that such elements are blades in the representational space because of

the o-dimension.

The ∞-dimension is new relative to the homogeneous model, and much more inter-

esting. If we draw the Euclidean 2-space as the e

∧ e

-plane, then there is apparently

a paraboloid (x,

∞) in the ∞-direction that we should get to know better, for the

points of Euclidean space are represented on it. By studying the combinations of points

on this paraboloid, we should be able to get an intuition on how the conformal model

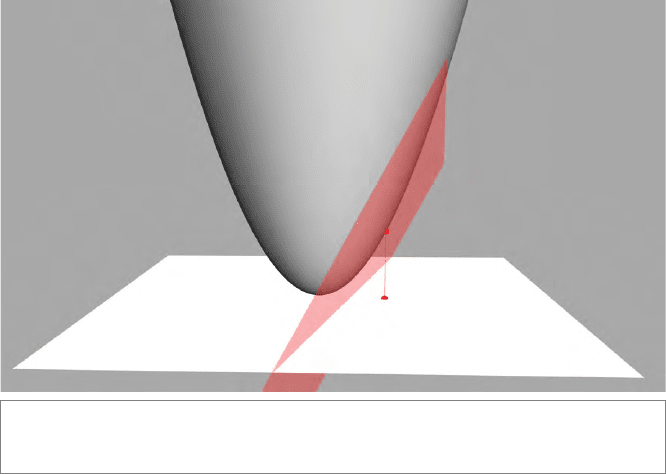
actually works. In Figure 14.3, you see the 2-D Euclidean space laid out in white, and the

∞-paraboloid indicated vertically above it.

A conformal null vector x representing a point ends on the paraboloid, just above

the point at the location x in the Euclidean plane which it represents. We draw it as the

parabola point with location vector x +

∞, letting the extra dimension o play the role

of the homogeneous coordinate. In Figure 14.3, we have drawn a vertical connecting line

between the point x and its representation; since that line runs in the ∞-direction, it is

represented by the line x ∧∞in this homogeneous depiction of the conformal model

SECTION 14.3 A VISUAL EXPLANATION OF ROUNDS AS BLADES 411

Figure14.3: Visualization of a 2-D Euclidean point X as a conformal vector x on the represen-

tative paraboloid of the conformal model. The tangent plane at x has the dual representation x.

(with x on it and ∞ as its direction). That vertical line is therefore the visualization of the

ﬂat point x ∧∞at the location of X.

We have also drawn a plane at x, tangent to the paraboloid. This is actually the representa-

tional plane x

∗

: it consists of all the vectors perpendicular to the vector x (in this metric).

(It doesn’t look perpendicular, but that is because we are interpreting with Euclidean eyes.)

This is a direct consequence of the null-vector representation of Euclidean points. A con-

formal vector y is on a plane Π if and only if y∧Π=0. Or, if we have a dual representation

of the plane, π =Π

∗

, then y is in the plane if and only if y ·π = 0. You will remember that

the metric of the conformal model is set up in such a way that x·x = 0, and the motivation

for that was that a point represented by x has distance 0 to itself in the Euclidean metric.

We now see that we can also read this as

If the vector x represents a Euclidean point, then x is on the tangent plane to the

paraboloid that is dually represented by x.

Since y = x is the only null vector that satisﬁes y ·x = 0, the plane dually represented by x

cannot intersect the paraboloid anywhere else, so it must indeed be the tangent plane to

the paraboloid.