Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

382 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

Figure 13.4: The computation of the screw corresponding to a rotor R followed by a trans-

lation over t. The rotor plane and angle are indicated by the blue disk. The translation w along

the screw axis is the rejection of t by the rotation plane. The location vector v of the axis is

found as the unique vector in the rotation plane whose chord under rotation is parallel to w − t

(indicated by a thin blue line). The resulting screw motion around the axis (in black) is shown

applied to a tangent bivector (in fading shades of green).

avectorv (which we can take to be in the I-plane without loss of generality), followed by

a translation w in the direction of that axis. We saw this form of the motion above, and

therefore ﬁnd that we need to solve

I␾

= T

I␾

]

for v and w,wherev ∧ I = 0 and wI = 0. The two factors on the right-hand side should

commute, since we can do the translation along the displaced axis before or after a rotation

around it. Actually, that demand on commutation is an equivalent, more algebraic way

of phrasing the problem, from which the conditions on v and w relative to I follow.

The Euclidean blade I characterizing the direction of the rotation plane can be computed

as the normalization of R

. Since the only translation perpendicular to I is performed

by w, we must have that w is the rejection of the translation vector t by I:

w = (t ∧ I)/I.

SECTION 13.5 RIGID BODY MOTIONS 383

That leaves the other part of the translation (tI)/I.Callitu for the moment. The problem

is now reduced to a 2-D problem in the I-plane, namely that of solving for v in

I␾

= T

I␾

−v

We would like to swap the rightmost translation with R

I␾

. We derive the following swap-

ping rule (abbreviating R

I␾

to R for convenience):

−v

= R (1 + v∞/2) = (1 + Rv∞



R /2) R = (1 + Rv



R ∞/2) R = T

−Rv



(13.12)

We also observe that since v isavectorintheR-plane, we have



R = v (



R 

+ 



R 

) = (



R 

−



R 

) v = (R

+ R

) v = R v.

Therefore,

R = T



= T

−Rv



R = T

v−Rv



R = T

v−R

R = T

(1−R

It follows that

v = (1 − R

)

−1

u = (1 − R

)

−1

(tI)/I. (13.13)

Graphically, the vector v − Rv



R = 2(vR)/R occurring in this computation is the chord

connecting the rotated v to the original v. We should ﬁnd v such that this equals u, which

gives the construction in Figure 13.4 as the geometric interpretation of this algebr aic com-

putation. To pull it all together, the ﬁnal result giving the screw parameters is:

screw decomposition: T

I␾

= T

(t∧I)/I

(1−R

␾

)

−1

(tI)/I

I␾

]

Realize again that T denotes a translation rotor, whereas

T[] denotes a translation

operator!

13.5.3 LOGARITHM OF A RIGID BODY MOTION

Using Chasles’ theorem, we can determine the logarithm of a rigid body motion rotor V,

which means that we can determine the bivector when we have been given the rotor. For

such a rotor is, on the one hand,

V = T

I␾

= (1 − t ∞/2) R

I␾

= R

I␾

−

t R

I␾

∞, (13.14)

and on the other hand,

V = T

[I␾]

= e

−w∞/2

−T

[I␾]/2

= e

−w∞/2−T

[I␾]/2

in which the addition of the exponents is only permitted because the rotors commute.

They were designed that way by Chasles’ theorem, and it is the algebraic consequence of

384 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

the possibility to execute the screw as one smooth motion. Substituting the values of w

and v we found above, the requested rigid body motion logar ithm is

log(T

I␾

) = −((t ∧ I)/I) ∞/2 + T

(1−R

)

−1

(tI)/I

[−I␾/2]

= −((t ∧ I)/I) ∞/2 + (1 − R

)

−1

(tI␾) ∞/2 − I␾/2

(13.15)

The value of this expression can be determined via the computation of the screw param-

eters, provided that we can retrie ve both R

I␾

(which gives I␾ by the logarithm of (10.14))

and t from the overall rotor V. But this retrieval is simple in (13.14):

I␾

= −o(V ∞), t = −2(oV )/R

I␾

Putting all formulas together, we get the pseudocode of Figure 13.5. Special cases happen

when R equals +1 or −1. When R equals +1, the motion is a pure translation versor and

we just return the logarithm of that (which is −t ∞ / 2).When R equals −1, there is no

unambigious logarithm, since a rotation of π within any plane could generate the −1.

To prevent spurious terms in the product with the translation versor, one must choose a

plane perpendicular to t. In 2-D, this is impossible, and the logarithm does not exist (as

we intimated in Section 7.4.4). Having the logarithm of a rigid body motion is a pow-

erful result. It permits us to interpolate these motions in a total analogy to the rotation

log(V){

R = −o(V∞)

t = −2(oV)/R

if (R == −1) return (“no unique logarithm”)

if (R == 1)

log = −t ∞/2

else

I = R



−R

␾ = −2 atan2



R

/I, R



log =



− (t ∧ I)/I + 1/(1 − R

) tI␾



∞/2 − I␾/2

endif

}

Figure 13.5: Computation of the logarithm of a normalized rigid body motion rotor V. One

may improve subsequent numerics by making sure to return a bivector by taking the grade-2

element by log

SECTION 13.6 APPLICATION: INTERPOLATION OF RIGID BODY MOTIONS 385

interpolation procedure that we had in the vector space model. See Section 13.10.4 for an

implementation.

13.6 APPLICATION: INTERPOLATION OF RIGID

BODY MOTIONS

According to Chasles’ theorem, a rigid body motion can be viewed as a screw motion.

It is then natural to interpolate the or iginal motion by performing this screw gradually.

Figure 13.6 shows how simple this has become: the ratio of two unit lines L

and L

deﬁnes

the square of the versor that transforms one into the other (see structural exercise 9).

Performing this motion in N steps implies using the versor

1/N

= e

log(L

)/(2N)

Applying this versor repeatedly to the line L

gives the ﬁgure. It interpolates the transfor-

mation of L

into L

and extrapolates naturally. Note how all can be deﬁned completely,

and simply, in terms of the geometric elements involved. You do not need coordinates to

specify how things move around. The same rotor V

1/N

can of course be applied to any

element that should move similarly to L

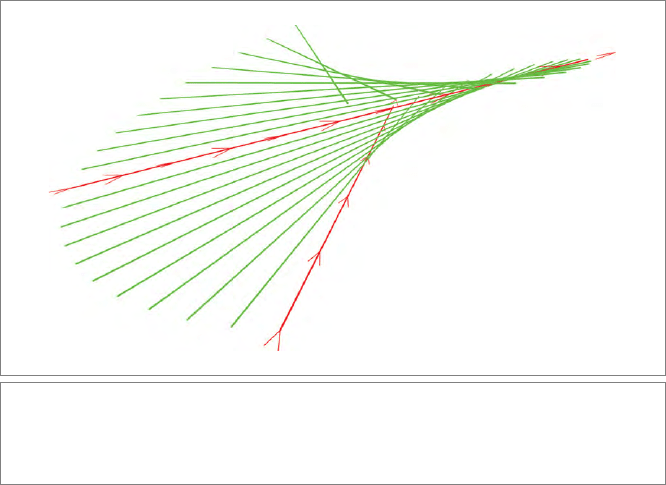
Figure 13.6: The interpolation and extrapolation of the rigid body motion transforming a

spatial line L

into a line L

is done by repeated application of the versor exp



log(L

)/(2N)



The screw nature of the motion is apparent.

386 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

Since the resulting logarithms are bivectors, they can be interpolated naturally themselves.

This allows one to estimate how various points on a rigid body move, establish their

motion bivectors, and average those to get an improved estimate of the motion. Such

numerical estimation techniques for motions are now being developed.

13.7 APPLICATION: DIFFERENTIAL PLANAR

REFLECTIONS

Now that we have general planar reﬂections available in (13.11), we can redo the exam-

ple of Section 8.5.2, in which we studied a rotating mirror and its reﬂected image using

geometric differentiation. Before, we used what was effectively the vector space model

and therefore could only work in the origin. Now we can treat the fully general planar

rotation.

To restate the problem, we consider the reﬂection of an element X in the dual plane π

(i.e., X → π



X π

−1

) in 3-D Euclidean space. We rotate the plane slightly around line Λ,

and need to ﬁnd out what this does to the reﬂection of X.

In Section 8.2.5, we performed the differential computation of such perturbed versors in

completely general form, with as a result (8.6) for the bivector of the perturbation versor,

given an original versor and a motion. We can apply this immediately, since the conformal

model gives us these versors: the original versor is the reﬂection versor π, and the motion

is exp(−Λ

−∗

␾/2) with bivector Λ

−∗

␾. Then according to application of (8.6), the versor

displacing the reﬂection should have bivector

−2␾ (π

x Λ

−∗

)/π = −2␾ (πΛ

−∗

) π = −2␾ (πΛ

−∗

) ∧ π = 2␾ (π ∧ Λ)

∗

∧ π

(13.16)

The geometr ic interpretation of π ∧ Λ is the plane perpendicular to π and containing the

line Λ; then the interpretation of the total formula is that it is dual of the

meet of this

plane with the dual plane π (i.e., it is dual of the orthogonal projection of the line Λ onto

the mirror π). This line is indicated in Figure 13.7(a). Since the bivector of the resulting

perturbing versor is this dual line, that versor is a rotation around this projected line when

the reﬂection plane changes. This is clear geometry, easily veriﬁed. When it rotates around

this line, the perturbed element follows a curved path: ﬁrst-order perturbat ions in versors

can lead to element paths of second order.

We would have to do a second-order Taylor series on the position to achieve a similar

effect, so not only are the versor perturbations structure-preserving but they also give us

a much better approximation for the same effort. You can work out the angle of rota-

tion of the perturbation in a similar way as in the origin-based treatment, again resulting

in (8.11).

Note that this computation is not valid for large perturbations: doing the same

construction on a per turbed mirror shows that the projected line changes (since it now

SECTION 13.7 APPLICATION: DIFFERENTIAL PLANAR REFLECTIONS 387

(a)

(b)

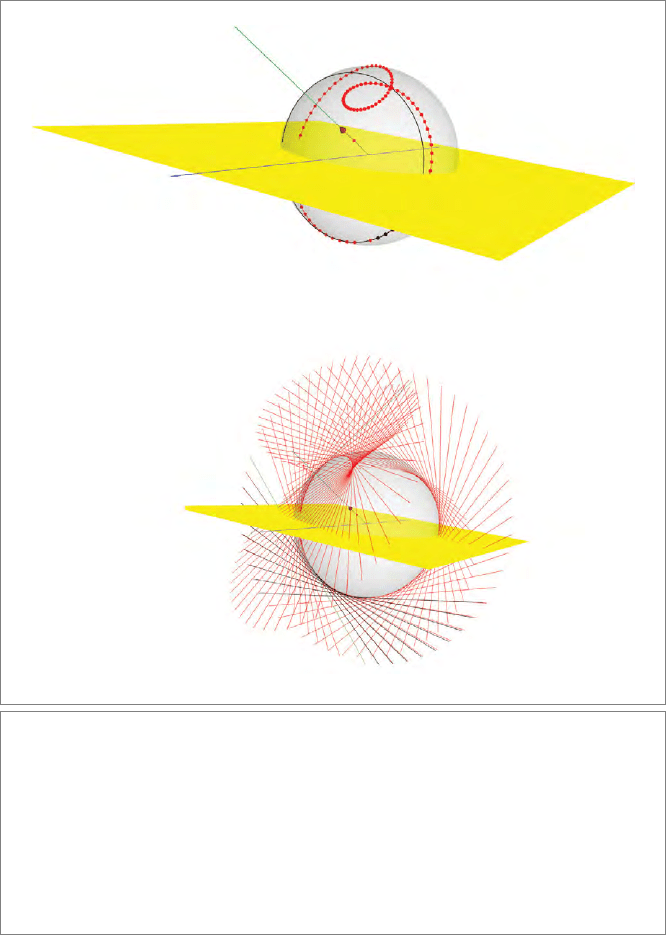
Figure 13.7: (a) The yellow planar mirror π reﬂects a point X to the point X

. The green line Λ

rotates the mirror; the red curve shows the orbit of the reﬂection in 100 steps. In black is the

ﬁrst-order perturbation description of the orbit around X

. It is a rotation of X

around the blue

line, which is the projection of the line Λ onto the mirror π, which follows the tangent circle

to the true orbit. The ﬁrst few black points keep pace with the red points, showing that the

velocity is correct. Note that a ﬁrst-order perturbation of the versor generates a second-order

curve. Both the black and red curves are on the sphere X ∧ π

∗

∧ Λ

∗

(perpendicular to both Λ

and π), which has also been depicted, to make the spatial nature of the curves more obvious.

(b) The same setup, merely replacing X by a line, to show the universality of constructions

in geometric algebra. The black lines are again good ﬁrst-order approximations to the exact

results.

388 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

needs to be on the perturbed mirror), and therefore the arc changes as well. In fact, it

becomes a caustic, of which the above effectively computes the local osculating cylinder.

Because we have done the whole computation in the conformal model, we can substitute

any of its other elements for X. Figure 13.7(b) shows the whole computation applied to a

reﬂected line. After the next chapter you w ill not even hesitate to apply it to the reﬂection

of a sphere, circle, or tangent blade.

13.8 FURTHER READING

The conformal model was ﬁrst introduced to the engineering community in 1999 [31],

but its roots can be traced to the 19th century. We will give more speciﬁc references

in the following chapters, when we have more a complete view of its contents and

capabilities.

Commercial applications of conformal geometric algebra to model statics, kinematics

and dynamics of par ticles and linked rigid bodies are protected by U.S. Patent 6,853,964,

“System for encoding and manipulating models of objects” [32]. Anyone contemplating

such applications should contact Alyn Rockwood or David Hestenes. The patent does not

restrict use of conformal geometric algebra for academic research and education or other

worthy purposes that are not commercial.

13.9 EXERCISES

13.9.1 DRILLS

These drills intend to familiarize you with the form of common geometric elements and

their parameters in the conformal model. We recommend doing them by hand ﬁrst, and

check them with interactive software later.

1. Give the representation of a point p

with weight 2 at location e

+ e

2. Give the representation of a point p

with weight −1 at location e

, and compute

its distance to p

3. Give the representation of the line L through p

and p

4. Compute weight and direction of the line L.

5. Compute the support point on the line L.

6. Give the direct representation of the plane Π through L and the unit point at the

origin.

7. Compute the direction and support of the plane Π.

8. Give the representation of the translation over −e

of the plane Π.

SECTION 13.9 EXERCISES 389

9. Compute the dual π of the plane Π. Compute its dual direction and its moment.

10. Compute the dual of the line L.

13.9.2 STRUCTURAL EXERCISES

1. Show that on the {e,

e}-basis, the point p of (13.3) is represented as:

p = p +

(1 − p

) e +

(1 + p

)

In [33] and [15], you ﬁnd the close relationship of this formula with stereographic

projection spelled out as a way of visualizing of the conformal model. Unfortunately,

it needs the two extra dimensions, so you can only visualize the model for a 1-D

Euclidean space. We will provide a better visualization in Section 14.3.

2. Show that ∞ o ∞ = −2 ∞ and o ∞ o = −2 o.

3. In structural exercise 5 of Section 11.12.2, we introduced barycentric coordinates

using the homogeneous model. Using the correspondence between homogeneous

model and conformal model, give expressions for the barycentric coordinates in

terms of conformal points.

4. When studying dualization in combination with versors in the main text, we were

mostly interested in the even versors, for which V[X]

∗

= V[X

∗

].Foroddversors,

you should use V[X]

∗

= −V[X

∗

]. Derive both simultaneously by using the general

versor transformation of (7.18), which i s is V[X] = (−1)

VXV

−1

, to show that

V[X]

∗

= (−1)

V[X

∗

]. (Hint: What is the sign involved in swapping V

−1

n+1

−1

n+1

−1

5. For a pure translation versor T, the logarithm is easy to determine. Show that

log(T) =

(T −



T ).

6. Write the logarithm of the rigid body motion of (13.15) in terms of the logarithm

of the rotor R introduced in (10.14). Your goal is to eliminate all I or ␾ from the

formula.

7. Show that the ratio of two ﬂat points p ∧∞and q ∧∞is a t ranslation rotor. What

is the corresponding translation vector?

8. Show that the ratio of two general planes passing though a common point p is a

rotation versor. Do this in 3-D; you can represent the plane with normal n dually

as p(n ∧∞). The ratio of two elements is of course identical to the ratio of their

duals. What is the bivector angle of the rotation?

9. Show that the ratio of two lines p ∧ n ∧∞and q ∧ m ∧∞is a general rigid body

motion. What are the screw parameters?

390 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

10. To get back to an issue raised in Section 8.2.2, w ith translation represented as a rotor

you can indeed change the position of a point x arbitr arily within a multiplicative

framework. Show that the transformation by a translation rotor

= exp(−t ∞/2),

when developed in the Taylor series expansion (8.3), generates an arbit rary additive

change in the position of a point x.

13.10 PROGRAMMING EXAMPLES AND EXERCISES

The implementation of the conformal model of 3-D space is called c3ga. The basis of

the representation space in this implementation is spanned by basis vectors

no, e1, e2,

e3, and ni, with the metric as in Table 13.1. As you notice, we write o and ∞ as no and

ni in our code (short for null vector representing the origin and null vector representing

inﬁnity, respectively).

This, ﬁnally, is the implementation of geometric algebra that is

behind the code of Figure 1.2 in the introductory example of Section 1.1.

The implementation contains a large number of specialized multivector types. Table 13.3

lists the most important ones. We have so far only t reated the ﬂats, the directions (labeled

“free” in the table), and the rigid body motion operators (the table uses “rotor” exclusively

for a rotation versor, calling a translation rotor a “translator”). The other elements will

be introduced in the next chapter.

The specialized multivector types are complemented by the matrix representation of out-

ermorphisms (

om) and a specialized matrix representation that works well with OpenGL

(

omFlatPoint).

In addition to the basis vectors, which are present as constants by default,

c3ga also con-

tains some extra constants (see Table 13.4).

A 2-D version of the conformal model implementation is also provided. It is named

c2ga and has most of the same specialized multivector types as its 3-D counterpart, but

of course lacks

spheres, freeTrivectors, and so on. We use c2ga in Sections 14.9.1

and 15.8.2.

13.10.1 METRIC MATTERS

As a ﬁrst experiment to conﬁrm that c3ga uses the strange metric of the conformal model,

we pr int out the metr ic of the ﬁve basis vectors:

// get the basis vectors:

mv bv[5] = {no, e1, e2, e3, ni};

// ... (omitted)

for (int i=0;i<5;i++) {

5 When pronounced in a sentence, ni should be emphatic and slightly higher than the other words, whereas no

should sound like a man imitating a woman imitating a man’s voice.

SECTION 13.10 PROGRAMMING EXAMPLES AND EXERCISES 391

// ... (omitted)

for (int j=0;j<5;j++) {

printf(" % 1.1f", _Float(bv[i] << bv[j]));

}

printf(

"\n");

}

Table 13.3: A list of the most important specialized multivector types in c3ga .

Name Sum of Basis Blades

vector e1, e2, e3

point no, e1, e2, e3, ni

normalizedPoint no =1,e1, e2, e3, ni

flatPoint e1∧ni, e2∧ni, e3∧ni, no∧ni

pointPair no∧e1, no∧e2, no∧e3, e1∧e2, e2∧e3,

e3∧e1, e1∧ni, e2∧ni, e3∧ni, no∧ni

line e1∧e2∧ni, e1∧e3∧ni, e2∧e3∧ni, e1∧no∧ni, e2∧no∧ni, e3∧no∧ni

dualLine e1∧e2, e1∧e3, e2∧e3, e1∧ni, e2∧ni, e3∧ni

plane e1∧e2∧e3∧ni, e1∧e2∧no∧ni, e1∧e3∧no∧ni, e2∧e3∧no∧ni

dualPlane e1, e2, e3, ni

circle e2∧e3∧ni, e3∧e1∧ni, e1∧e2∧ni, no∧e3∧ni, no∧e1∧ni,

no∧e2∧ni, no∧e2∧e3, no∧e1∧e3, no∧e1∧e2, e1∧e2∧e3

sphere e1∧e2∧e3∧ni, e1∧e2∧no∧ni, e1∧e3∧no∧ni, e2∧e3∧no∧ni, e1∧e2∧e3∧no

dualSphere no, e1, e2, e3, ni

freeVector e1∧ni, e2∧ni, e3∧ni

freeBivector e1∧e2∧ni, e2∧e3∧ni, e3∧e1∧ni

freeTrivector e1∧e2∧e3∧ni

tangentVector no∧e1, no∧e2, no∧e3, e1∧e2, e2∧e3, e3∧e1, e1∧ni, e2∧ni, e3∧ni, no∧ni

tangentBivector e1∧e2∧e3, e2∧e3∧ni, e3∧e1∧ni, e1∧e2∧ni, no∧e3∧ni,

no∧e1∧ni, no∧e2∧ni, no∧e2∧e3, no∧e1∧e3, no∧e1∧e2

vectorE2GA e1, e2

vectorE3GA e1, e2, e3

bivectorE3GA e1∧e2, e2∧e3, e3∧e1

translator scalar, e1∧ni, e2∧ni, e3∧ni

normalizedTranslator scalar=1, e1∧ni, e2∧ni, e3∧ni

rotor scalar, e1∧e2, e2∧e3, e3∧e1

scalor scalar, no ∧ ni