Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

392 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

Table 13.4: Constants in c3ga.

Name Value

e1ni e

∧∞

e2ni e

∧∞

e3ni e

∧∞

noni o ∧∞

I3 e

∧ e

I5 o ∧ e

∧ e

∧∞

I5i (o ∧ e

∧ e

∧∞)

−1

(We omitted some code that prints out the names.) The output of this part of the example

agrees with Table 13.1:

no e1 e2 e3 ni

no 0.0 0.0 0.0 0.0 — 1.0

e1 0.0 1.0 0.0 0.0 0.0

e2 0.0 0.0 1.0 0.0 0.0

e3 0.0 0.0 0.0 1.0 0.0

ni — 1.0 0.0 0.0 0.0 0.0

The example also creates vectors e (denoted as ep) and

e (denoted as em) from no and ni,

according to (13.6):

// create ’e+’ and ’e — ’

dualSphere ep = _dualSphere(no — 0.5f

ni);

dualSphere em = _dualSphere(no + 0.5f

ni);

Note that dualSphere is now the specialized vector type that holds arbitr ary 5-D vectors.

The example continues to print out some information about e and

e. T he output is

e+ = 1.00

no — 0.50

e — = 1.00

no + 0.50

The metric of e+ and e —:

e+ . e+ = 1.000000

e — . e — = —1.000000

e+ . e — = 0.000000

13.10.2 EXERCISE: THE DISTANCE BETWEEN POINTS

This example draws ﬁve (draggable) points, connected by lines, and prints distance labels

halfway between each pair of points. The exercise is to complete the following code:

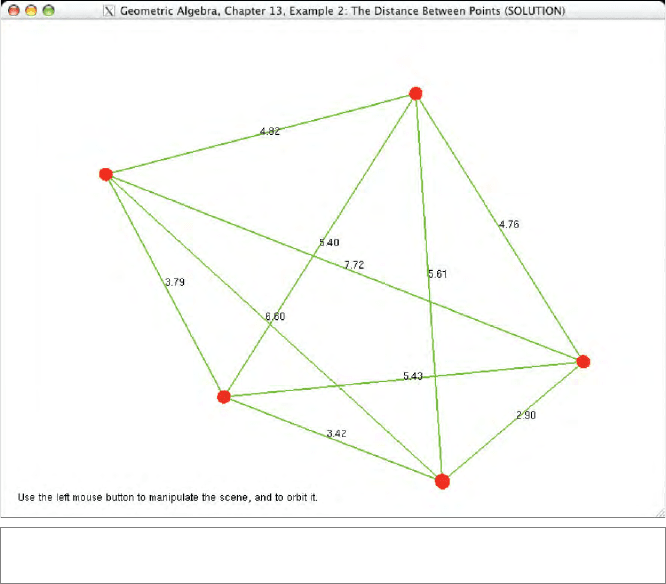
SECTION 13.10 PROGRAMMING EXAMPLES AND EXERCISES 393

Figure 13.8: The output of the solution to Example 2.

const normalizedPoint &pt1 = g_points[i];

const normalizedPoint &pt2 = g_points[j];

// compute distance

// EXERCISE: fill in the code to compute the distance between pt1

// and pt2

float distance = 0.0;

Figure 13.8 shows sample output of the correct solution. If you want to write a robust

solution, keep in mind that ﬂoating point roundoff error may cause values that should

always be less than or equal to zero to turn up as a very small positive number. This may

cause trouble when you hand this value (negated) to

sqrt().

13.10.3 LOADING TRANSFORMATIONS INTO OPENGL, AGAIN

In this exercise we repeat the example from Section 12.5.1, but this time we use the con-

formal model. The goal is to build up the matrix representation of any outermorphism

(in this case, a simple combination of translation and rotation) and to load that matrix

into OpenGL.

394 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

Figure 13.9: Example 4 in action. A trail of circles is drawn to visualize the interpolation of

rigid body motions.

In the homogeneous version, we transformed the basis vectors e

, e

, and e

, and used

their images to initialize the matrix representation of the transform. We then loaded this

matrix directly into OpenGL.

In the conformal model, the blades e

∧∞, e

∧∞, and o ∧∞are the closest

equivalent to the aforementioned basis vectors of the homogeneous model, since that is

how the two models relate to each other. Geometrically, these are the blades representing

the basis directions, just as e

, e

, and e

were in the homogeneous model. Using this,

the code to load our conformal outermorphism into OpenGL is

// get translator and rotor

vectorE3GA t = _vectorE3GA(distance

e3);

normalizedTranslator T = exp(_freeVector( — 0.5f

(t ^ ni)));

rotor &R = g_modelRotor;

// combine ’T’ and ’R’ to form translation—rotation versor:

TRversor TR = _TRversor(T

R);

TRversor TRi = _TRversor(inverse(TR)); // compute inverse

SECTION 13.10 PROGRAMMING EXAMPLES AND EXERCISES 395

// compute images of basis blades e1^ni, e2^ni, e3^ni, no^ni:

flatPoint imageOfE1NI = _flatPoint(TR

e1ni

TRi);

flatPoint imageOfE2NI = _flatPoint(TR

e2ni

TRi);

flatPoint imageOfE3NI = _flatPoint(TR

e3ni

TRi);

flatPoint imageOfNONI = _flatPoint(TR

noni

TRi);

// create matrix representation:

omFlatPoint M(imageOfE1NI, imageOfE2NI, imageOfE3NI, imageOfNONI);

// load matrix representation into GL:

glLoadMatrixf(M.m_c);

In Section 16.10.1, we will perform the opposite operation of converting OpenGL matri-

ces to conformal versors. We postpone this subject until we can properly handle (uniform)

scaling, which is ﬁrst introduced in Chapter 16.

13.10.4 INTERPOLATION OF RIGID BODY MOTIONS

Since we can now represent translation and rotation as exponentials of bivectors and have

their logarithm available (see Section 13.5.3), we can interpolate them with ease. The

example presented here is similar to the interpolation example treated in the context of

the vector space model (Section 10.7.1), but the conformal model now allows us to do it

properly.

First of all, we need an implementation of the logarithm of (normalized) translation-

rotation versors. This is easily done given the pseudocode in Figure 13.5:

dualLine log(const TRversor &V) {

// isolate rotation & translation part:

rotor R = _rotor( — no << (V

ni));

vectorE3GA t = _vectorE3GA( — 2.0f

(no << V)

inverse(R));

const float EPSILON = 1e — 6f;

if (_Float(norm_e2(_bivectorE3GA(R))) < EPSILON

EPSILON) {

// special cases:

if (_Float(R) < 0.0f)

{//R= —1

// Get a rotation plane ’I’, perpendicular to ’t’

bivectorE3GA I;

if (_Float(norm_e2(t)) > EPSILON

EPSILON)

I = _bivectorE3GA(unit_e(t << I3));

else {

//whent=0,anyplane will do

I = _bivectorE3GA(e1^e2);

}

// return translation plus 360 degree rotation:

return _dualLine(0.5f

2.0f

(float)M_PI - (t^ni)));

}

else

396 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

{ //R=1;

// return translation :

return _dualLine( — 0.5f

(t^ni));

}

else { // regular case

// compute logarithm of rotation part

bivectorE3GA Iphi = _bivectorE3GA( — 2.0f

log(R));

// determine rotation plane:

rotor I = _rotor(unit_e(Iphi));

// compose log of V:

return _dualLine(

0.5f

(

—(t^I)

inverse(I)

ni +

inverse(1.0f — R

(t << Iphi)

ni —

Iphi));

}

Note the slight misuse of the type system: the function returns a dualLine,whichisofﬁ-

cially a 2-blade. In general, the logarithm of a rigid body motion is not a 2-blade but

a bivector. It just so happens that this bivector can be represented employing the same

basis blades as for dual lines, so we can (ab-)use

dualLine as the return type. That is

a consequence of the additive decomposition. But if you would pass the output of this

log() function to draw(), which can only draw blade, it will only draw a line if the screw

happens to be a pure rotation.

The example interpolates from one random versor to the next. These versors are com-

puted as the product of a random translation and a random translated rotation:

void initRandomDest() {

normalizedTranslator T1 = exp(_freeVector(randomBlade(2, 3.0f)));

normalizedTranslator T2 = exp(_freeVector(randomBlade(2, 3.0f)));

rotor R = exp(_bivectorE3GA(randomBlade(2, 100.0f)));

g_destVersor = _TRversor(T1

inverse(T2));

}

Interpolation between the versors is done using the following function, which is almost

identical to the one used in Section 10.7.1:

// interpolate between ’src’ and ’dst’, as determined by ’alpha’

TRversor interpolateTRversor(const TRversor &src,

const TRversor &dst, mv::Float alpha) {

// return src

exp(alpha

log(inverse(src)

dst));

return _TRversor(src

exp(_dualLine(alpha

log(_TRversor(inverse(src)

dst)))));

}

NEW PRIMITIVES FOR

EUCLIDEAN GEOMETRY

This chapter continues the development of the conformal model of Euclidean geometry.

We have seen in the previous chapter how the model includes ﬂats and directions as blades

and Euclidean transformations on them as versors. That more or less copied the capabil-

ities of the more familiar homogeneous model, though in a structure-preserving form,

which permits metrically signiﬁcant interpolation.

In this chapter, we show that the blades of the conformal model can represent many

more elements that are useful in Euclidean geometry: They give us spheres, circles,

point pairs, and tangents as direct elements of computation. Having those available

will extend the range of computations that can be done by the basic products of geo-

metric algebra, which is the subject of the next chapter. Here we carefully develop the

representation of these new elements and show how to retrieve their parameters. You

will for instance see that the sphere through the four points p, q, r, and s is the blade

p ∧ q ∧ r ∧ s, and that you can immediately read off its center and radius from the dual

sphere (p ∧ q ∧ r ∧ s)

∗

Again, we urge the use of interactive visualization to get the maximum enjoyment out of

this chapter. The conformal model is not abstract mathematics, it is a practical tool!

397

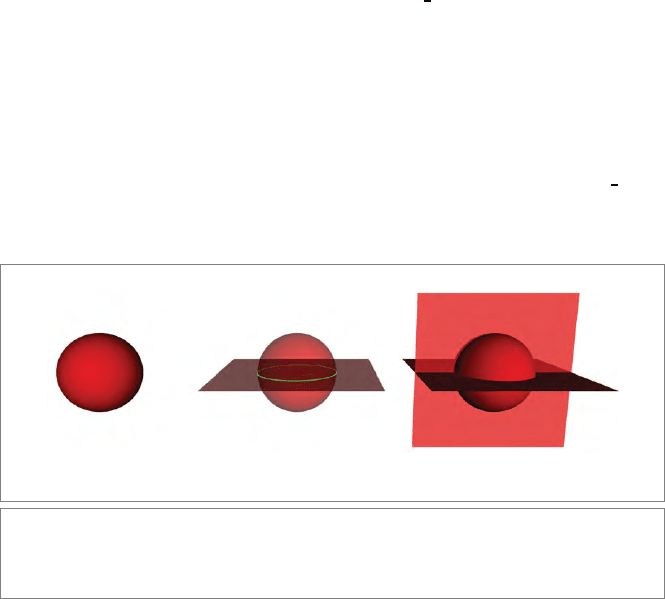
398 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

14.1 ROUNDS

We have made the representation of ﬂats by considering blades containing the point at

inﬁnity ∞. We can make other blades through the outer product of ﬁnite points only.

It is a happy surprise that this gives us the direct representations of spheres, circles, and

other related elements. For such elements we do not have the analogy of the homogeneous

model to guide us, and it is actually somewhat easier to introduce them through their

duals and then derive their direct representation from that. Once we have the results,

either mode is easy to work in, it just depends on the manner in which your data has been

given (we will ﬁnd that if you know the center and radius of a sphere, you should use

the dual to construct its blade; if you know four points on the sphere, you should use the

direct representation).

14.1.1 DUAL ROUNDS

We start with the dual representation of a real sphere of radius ρ, located at the origin o

(see Figure 14.1(a)). According to Table 13.2, this is

dual sphere at origin: σ = o −

∞.

Let us cut this dual origin sphere with a plane through the origin, dually represented

as π = n. Such a plane is perpendicular to the sphere in our Euclidean base space. In

the representation, this perpendicularity of a plane and a sphere set corresponds to the

statement

π · σ = 0.

This is easily veriﬁed for the particular situation we have at the origin: n · (o −

∞)

= 0. The general result is achieved through the familiar argument on covariance: the

(a) (b) (c)

Figure 14.1: Dual rounds in the conformal model in 3-D, obtained by intersecting a sphere

with planes. (a) The dual sphere

σ, (b) the dual circle σ ∧ π (in green), and (c) the dual point

pair

σ ∧ π ∧ π



(in blue).

SECTION 14.1 ROUNDS 399

condition is formulated as a scalar-valued inner product; therefore, it is invariant under

orthogonal transformations; therefore, it is invariant under versors; therefore, when

both elements are rotated and translated it still holds; therefore, it holds universally as

the condition for perpendicularity of a sphere and a plane through its center. Again,

the structure preservation saves us proving statements in their most general form: one

example sufﬁces to make it true anywhere.

We can form the blade κ = σ ∧ π. Since this is the outer product of two duals, it must be

the dual representation of the

meet of plane and sphere (for (A ∩ B)

∗

= B

∗

∧A

∗

, see (5.8)).

In our Euclidean space, the

meet is clearly a circle (see Figure 14.1(b)), and if everything

is consistent, its dual representation, κ, must be a dual circle.

dual circle at origin: κ = σ ∧ π = (o −

∞) ∧ n,

where n is the dual representation of the carrier plane π of the circle. This is how simple

it is to represent a dual circle in the conformal model: it is a 2-blade.

If you are still suspicious whether this really is a dual circle, probe this dual element κ with

a point x and check for which points x this is zero. That gives the condition

0 = x(σ ∧ π) = (x · σ) π − (x · π) σ.

Then take the inner product of this with π, which gives 0 = (x · σ) π · π, and the inner

product with σ, which gives 0 = (x · π) σ · σ. Since both π · π and σ · σ are nonzero (at

the origin, and therefore everywhere) this indeed retrieves the independent conditions

x · σ = 0 and x · π = 0, so the point x must be both on the sphere and on the plane. In

Euclidean terms, the former condition is x

= ρ

, and the second is x · n = 0,whichis

clearly sufﬁcient to construct the circle equation x

+ x

= ρ

for coordinates of x in the

n-plane.

We can cut the circle with yet another plane π



, perpendicular to both σ and π (see Fig-

ure 14.1(c)). In 3-D, that gives us a dual point pair, which is indeed a sphere on a line, the

set of points with equal distance to the center o. It is dually represented as

dual point pair at origin: σ ∧ π ∧ π



The Euclidean bivector π



∧ π is the dual meet of the two planes, and dually denotes the

carrier line of the point pair. In an n-dimensional space, the process continues, and you

can cut the original sphere with n hyperplanes before the outer product trivially returns

zero (which makes geometric sense, since there are only n independent hyperplanes at the

origin in n-dimensional space).

Let us call the elements we obtain in this way dual rounds. Their general form, when cen-

tered on the origin, is

real dual round at origin: (o −

∞) E

(14.1)

with E

a purely Euclidean k-blade dually denoting the carrier ﬂat of the round. Since

the blades are generated in properly factored form, we will prefer to denote them using

400 NEW PRIMITIVES FOR EUCLIDEAN GEOMETRY CHAPTER 14

the geometric product; however, you could use the outer product instead (see structural

exercise 8). When we translate them by a translation over c, the dual sphere part moves

to c −

∞, whereas the purely Euclidean part changes according to (13.7) (i.e., to

−c(∞E

)). Therefore, the general form for a round centered at c is

real dual round at c: (c −

∞)



− c(∞E

)



. (14.2)

We will later relate the Euclidean blade E

to a speciﬁcally chosen orientation for the car-

rier ﬂat c ∧ A

n−k

∧∞, and then set E

= (−1)



n−k

to represent this same orientation

dually. For now, focus on the form of the expression rather than on such details.

We started from a real dual sphere to produce these elements; had we started from an

imaginary sphere o+

∞(see Section 13.1.3), we would have produced dual imaginary

rounds. These therefore only differ from the real rounds in replacing ρ

by −ρ

.Aswe

saw before, we can have representation of imaginary rounds in a real algebra, since only

squared distances enter our computations.

You may wonder why we did not encounter imaginary ﬂats in the previous chapters. But

ﬂats are always real, for they have no size measure like a radius. They merely have a weight,

and when its sign changes, this simply changes their orientation. Of course, rounds also

have a weight, which gives them an orientation and a density.

14.1.2 DIRECT ROUNDS

Now that we have made dual spheres, circles, and point pairs, real or imaginary, we also

want to know their direct representation: they will give us yet another type of blade in the

conformal model

n+1,1

with a clear geometric meaning in E

Instead of undualizing the duals, we now have enough experience with the conformal

model to guess the direct representation and then relate it to the duals afterwards. The

resulting computation is surprisingly easy and coordinate-free, and a good example of

the kind of symbolic computational power the operational model of Euclidean geometry

affords.

Let us consider the 3-D Euclidean space

. A sphere in that space is determined by four

points. We take four unit points p, q, r, s. We are bold and guess that the sphere Σ is

represented by the blade

Σ=p ∧ q ∧ r ∧ s,

but of course we should prove that. First, we manipulate it using the antisymmetry of the

outer product, subtracting p from all terms but the ﬁrst, to obtain

Σ=p ∧ ( q − p) ∧ (r − p) ∧ (s − p).

Then we dualize, producing

SECTION 14.1 ROUNDS 401

∗

= p



(q − p) ∧ (r − p) ∧ (s − p)



∗

(14.3)

We suspect that this might be a dual sphere, but this is in a form we have not seen

before: it is apparently characterized by a point on it contracted on something else. From

Table (13.2), we only know it in the form c −

∞, given its unit center point c and

radius ρ. But if we know a unit point p on the sphere, then ρ is easily computed through

p · c = −

, and using p ·∞= −1, we can group these results in a compact form:

dual sphere around c through p: p(c ∧∞).

(14.4)

We recognize c ∧∞as the ﬂat point at the center of the sphere.

Returning to (14.3), if Σ

∗

is supposed to be a dual sphere through p, then the expression

under the dual should be a representation of the ﬂat point at the center, possibly weighted.

From its form, it is the

meet of three elements that are dually represented by (q−p), (r−p),

and (s −p). What is (q −p)? Since it is a dual representation of some element, we probe it

with a point x to ﬁnd out: 0 = x · (q − p),sox · p = x · q,sod

(x,p) = d

(x,q).Itfollows

that

q − p is the dual midplane between the unit points p and q.

(14.5)

So the expression



(q − p) ∧ (r − p) ∧ (s − p)



∗

computes the intersection of the mid-

planes between the three point pairs, which is indeed a weighted copy of the ﬂat point

at the center α ( c ∧∞). Therefore we indeed have a (weighted) dual sphere. It follows that

the outer product of four points is a sphere.

The relationship between dual and direct representation of the sphere,

α (c −

∞) = (p ∧ q ∧ r ∧ s)

∗

implies that the (center, radius) formulation is exactly dual to the four-point deﬁnition.

We can compute the weight α by taking the contraction with −∞ on both sides, giving

α = −∞(p ∧ q ∧ r ∧ s)

∗

= −(∞∧p ∧ q ∧ r ∧ s)

∗

This give us an easy way to compute the squared radius of a sphere through four points

as the square of the corresponding normalized dual sphere. Some duals and signs cancel,

and we get

= (c −

∞)



(p ∧ q ∧ r ∧ s)

∗



/α

(p ∧ q ∧ r ∧ s)

(p ∧ q ∧ r ∧ s ∧∞)

1 To do things properly, we have to make sure the signs are consistent between the dual and the direct represen-

tation. You see that the intersection expression deviates from a

meet in two aspects: it involves the wrong order

(for a

meet would normally swap the order of the arguments), and it uses the dual rather than the inverse dual.

However, both involve a reversion of

n elements in an n-dimensional base space, so the overall sign cancels. The

result is therefore correct.