Dorst L., Fontijne D., Mann S. Geometric Algebra for Computer Science. An Object Oriented Approach to Geometry

Подождите немного. Документ загружается.

372 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

product is a geometric product, and we have (o ∧∞)(x ∧ A

) = 0 (absorbing a sign into

the zero). The model bivector o ∧∞is not zero, so we must have x ∧ A

= 0 (if you do not

trust this reasoning, take the contraction of the original equation with o ∧∞to eliminate

the non-Euclidean part, and use (o ∧∞)(o ∧∞) = (∞·o)

= 1). But the result

x ∧ A

= 0

is a simple equation from the vector space model. It involves purely Euclidean vectors and

implies that x is in the blade spanned by A

. Therefore the blade X = o∧A

∧∞represents

a ﬂat k-dimensional subspace through the origin o.

Generalization

We have found that ﬂats through the origin are part of the conformal model, and since the

Euclidean transformations are structure-preserving, all their translations and rotations

should be in the model as well.

To ﬁnd the general form of a k-dimensional ﬂat through a point p, we need to translate

o ∧ A

∧∞using the versor T

. Since this is a versor, we can distribute it over the terms o,

, and ∞. The ﬁrst and the last are easy: T

applied to o is p, and ∞ is invariant, so the

translation of X is p ∧

] ∧∞. The translation of the Euclidean k-blade A

requires

some care:

] = (1 − p∞/2) A

(1 + p∞/2)

= A

−

(p∞A

− A

p∞) − p∞A

p∞/4

= A

∞ (pA

−



p) + 0

= A

+ ∞(pA

) = −p(∞A

). (13.7)

where p =

[o]. The ﬁnal form is a multiplicative rewriting convenient for later compu-

tations. For our present purpose, the penultimate form is more convenient. Substituting

it in p ∧

] ∧∞, we ﬁnd that its ∞-component is killed by the outer product with ∞,

so that the general form of a ﬂat k-dimensional offset subspace passing through p is

direct A

-ﬂat through p: p ∧ A

∧∞.

(13.8)

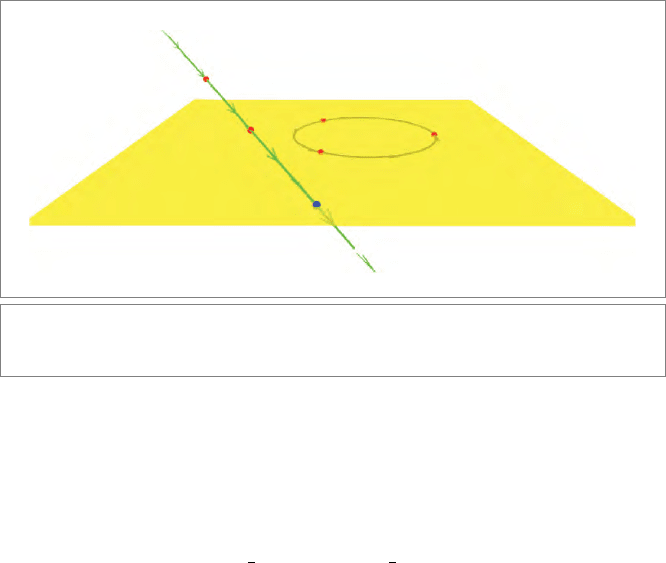
Elements of this kind are depicted in Figure 13.2.

We see that a directly represented ﬂat X in the conformal model always contains the point

at inﬁnity, so it satisﬁes ∞∧X = 0. In the origin, you can easily verify that X



X = −A



= 0, and since that is an invariant property, this holds anywhere. These

two conditions characterize the blades representing a direct ﬂat.

13.3.2 CORRESPONDENCE WITH THE HOMOGENEOUS MODEL

This expression p ∧ A

∧∞for a general direct ﬂat in the conformal model is nicely

backwards compatible with the homogeneous model. We can see this most clearly by

SECTION 13.3 FLATS AND DIRECTIONS 373

s ∧ t ∧

⬁

p ∧ q ∧ r ∧

⬁

u ∧

⬁

Figure13.2: Flat elements in the conformal model: the plane p∧q∧ r∧∞ (with its orientation

denoted by the circle), the line s ∧ t ∧∞, and the ﬂat point u ∧∞at their intersection.

trying to determine its meaning directly (without using the versor properties to bring

things to the origin, as we did above). So we need to solve 0 = x ∧ (p ∧ A

∧∞);it

simpliﬁes by the following steps:

0 = x ∧ (p ∧ A

∧∞)

= (o + x +

∞) ∧ (o + p +

∞) ∧ A

∧∞

= (o + x) ∧ (o + p) ∧ A

∧∞



o ∧ (p − x) + x ∧ p



∧ A

∧∞

= o ∧ (p − x) ∧ A

∧∞+ x ∧ (p − x) ∧ A

∧∞.

The linear independence of the two terms implies that they should each be zero to make

the total zero. The orthogonality of o ∧∞to the Euclidean parts makes setting the ﬁrst

term equal to zero equivalent to solving the single equation (p − x) ∧ A

= 0. The second

term is then also zero, so this is the general solution. We indeed have an offset ﬂat with

direction element A

passing through the point at p.

After the ﬁrst two steps, this derivation is completely analogous to the computation in the

homogeneous model:

0 = (e

+ x) ∧ (e

+ p) ∧ A



∧ (p − x) + x ∧ p



∧ A



∧ (p − x) + x ∧ (p − x)



∧ A

Themetricpropertiesofo or e

(which are very different: o

= 0 while e

= ±1)donot

enter the solution process, they only serve as bookkeeping devices for the outer product.

374 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

This equivalence of the derivations worked because the outer product with ∞ removed the

terms involving the squared vectors from the point representation. We have demonstrated

an important relationship between the two models:

The homogeneous model is embedded in the conformal model as governing the behav-

ior of the blades involving a factor ∞. These represent offset ﬂat subspaces.

Pushing this equivalence, a homogeneous point p is found in the conformal model as the

element p ∧∞, which must be a ﬂat point. It contains both the conformal point represen-

tative p and the point at inﬁnity ∞. Such ﬂat points occur as the result of the intersection

of a line and a plane, which actually contains two common points: the ﬁnite intersection

point and the point at inﬁnity. An example is the point u ∧∞in Figure 13.2. In contain-

ing this inﬁnite aspect, they are subtly different from the point p itself, which is a dual

sphere with zero radius, as we saw in Section 13.1.3. Separating these algebraically is nat-

ural in the conformal model and cleans up computational aspects. But we readily admit

that these two conceptions of what still looks like a point in the Euclidean space

take some getting used to.

Anyway, if you want the line through the points p and q, this is the 2-blade p

∧ q

in the

homogeneous model (where p

and q

are the homogeneous representatives), and the

3-blade Λ=p ∧ q ∧∞in the conformal model. It can be re-expressed as p∧ (q − p) ∧∞ =

p∧(q−p)∧∞ ≡ p∧a∧∞, so the line passing through p with direction vector a is p∧a∧∞,

just as it would have been p

∧ a in the homogeneous model. Our ﬂexible computational

rerepresentation techniques from the homogeneous model therefore still apply without

essential change. In the conformal model, too, lines and planes can be represented by a

mixture of locations and/or directions, with the outer product as universal construction

operation.

13.3.3 DUAL REPRESENTATION OF FLATS

The dual representation of ﬂats is simply found by dualization. As a pseudoscalar for the

representational space

n+1,1

we use the blade representing the full Euclidean space as a

ﬂat, so

pseudoscalar of conformal model: I

n+1,1

≡ o ∧ I

∧∞,

where I

is the Euclidean unit pseudoscalar. As in the homogeneous model, we will denote

the dualization in the full representational space by a six-pointed star (as X

∗

) and the

dualization in its Euclidean part by a ﬁve-pointed star (as X

夹

, typically done on a purely

Euclidean element).

Dualization in geometric algebra involves the inverse of the unit pseudoscalar. In the

strange metric of the representational space

n+1,1

, this is not equal to the reverse of I

n+1,1

The reason boils down to a property of the 2-blade o ∧∞.Forwehave

(o ∧∞)(o ∧∞) = (o ∞ + 1) (o ∞ + 1) = o ∞ o ∞ + 2 o ∞ + 1 = 1

SECTION 13.3 FLATS AND DIRECTIONS 375

so that the o ∧∞is its own inverse. (The ﬁnal step involves a computation highlighted in

structural exercise 2.) The inverse of the pseudoscalar is then easily veriﬁed to be

−1

n+1

= o ∧ I

−1

∧∞,

so this is what we should use for dualization. It is satisfactory that the embedding of the

Euclidean model is such that the inverse of the representation of the Euclidean pseudoscalar

is the representation of the inverse. This is of course related to the general structure pre-

serving properties of the conformal model. We did not have this property in the homo-

geneous model, where (e

)

−1

= I

−1

= (−1)

−1

, involving an extra sign in

odd dimensions. Because we have two extra representational dimensions in the conformal

model (rather than just one), we can avoid those extraneous signs.

The structure-preserving property of the duality implies that we can make the dual of the

standard ﬂat through the origin and then translate it to the location of the desired ﬂat to

obtain its dual. This is permitted, for the structure preservation

V[X]

∗

= V[X

∗

]

holds for any even versor, especially for Euclidean motions. In the conformal model, we

do not need to know whether an element is a direct or a dual representation to move

it in a Euclidean manner by an even versor. This is an improvement over the homoge-

neous model. (However, in structural exercise 4, we ask you to show that there is an addi-

tional minus sign for an odd versor. So there is a small difference between reﬂections and

motions.)

Dualizing the origin blade o ∧ A

∧∞,weﬁnd

(o ∧ A

∧∞)

∗

= (o ∧ A

∧∞)( o ∧ I

−1

∧∞)

= −(o ∧ A

)(I

−1

∧∞)

= −o(A

夹

∧∞)



夹

Note that the grade inversion extends over the Euclidean dual, so it gives a sign of (−1)

n−k

The dual of a blade in the homogeneous model involved a similar sign change, so we are

still backwards compatible in the dualization.

But in contrast to the homogeneous model (see Section 11.8.2), translations on dual

blades are performed by the same operation as translations on direct blades: simply apply

the t ranslation versor. We have already computed the translation of a purely Euclidean

element in (13.7), so the result is immediate:

dual ﬂat:

[



夹

] =



夹

+ ∞(p



夹

) = −p(A

夹

∞).

(13.9)

376 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

This makes it particularly easy to construct, say, the dual representation of a hyperplane

with 2-blade I and associated normal n = I

∗

, passing through p:itisΠ

∗

= −p(n ∞) =

−n − (p · n) ∞. This conﬁrms our earlier result of Table 13.2, though the sign is now

properly related to a properly oriented plane Π and a well-deﬁned pseudoscalar in the

dualization process.

Direct representations of ﬂats contain a factor ∞ and are therefore characterized by ∞∧

X = 0. Dualization of this condition yields that a blade X

∗

representing a dual ﬂat is

characterized by ∞X

∗

= 0. This is of course interpreted to mean that the point at inﬁnity

is contained in the element dually represented by X. The condition itself is invariant under

Euclidean transformations, because ∞ is. The other property of a direct ﬂat, X

< 0,

dualizes to X

∗



> 0 for the dual representation.

13.3.4 DIRECTIONS

In the construction of the direct ﬂat p ∧ A

∧∞, we recognize the location p and the blade

∧∞. Bearing in mind how the conformal ﬂats correspond to their representations in

the homogeneous model, such an element A

∧∞must be the conformal representation

of a k-dimensional direction:

directly represented direction: A

∧∞.

To be a pure direction, it should only have directional properties and no locational aspects.

It is easy to verify how it transforms under a general Euclidean motion consisting of a

rotation

R and a translation T:

[R[A

∧∞]] =



R[A

] − (tR[A

]) ∞



∧∞= R[A

] ∧∞.

So these elements of the form A

∧∞are rotation covariant, but translation invariant.

That is precisely what you would expect from directions. The dual directions are simply

their duals:

dual direction: (A

∧∞)

∗

= (A

∧∞)( o ∧ I

−1

∧∞) = −A

夹

∧∞,

again involving signs that should be observed if you want to use them in consistently

oriented computations. They are clearly also translation invariant.

You can make a ﬂat by attaching a direction element to a point p using an outer product,

as in p ∧ (A

∧∞). The corresponding dual ﬂat is made by attaching the dual direction to

the point p using the contraction, giving p( −A

夹

∞) in agreement with (13.9).

A direction element X is characterized by containing ∞, so that ∞∧X = 0, and moreover

by having a zero norm: X

= 0, as you can easily verify. A dual direction X

∗

has ∞X

∗

0 and X

∗



= 0.

SECTION 13.4 APPLICATION: GENERAL PLANAR REFLECTION 377

13.4 APPLICATION: GENERAL PLANAR REFLECTION

In classical texts on subjects like computer graphics, many crucial formulas are given in

a Euclidean or homogeneous-coordinate form. How are we to integrate those into the

new conformal model? This is often surprisingly straightforward, since the more familiar

vector space model and the homogeneous model are both naturally contained in the con-

formal model. All that is required is recasting of standard formulas into a geometric alge-

bra format before you perform the embedding. You then ﬁnd that the conformal model

gives you the freedom to generalize the formulas, in a manner that the other models did

not allow. The reason, as always, is the versor form of the Euclidean transformations and

its associated structure-preserving properties.

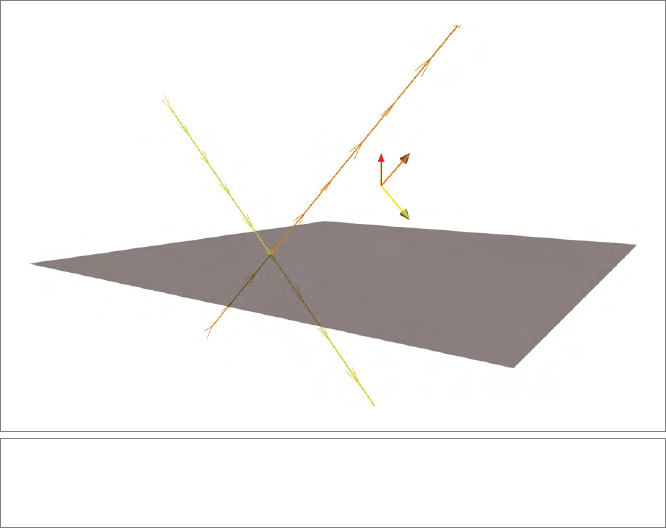
As an application, let us consider the reﬂection of a general line Λ in a general plane π.

See Figure 13.3.

•

Classical Linear Algebra. In the classical way of doing this, you would have to treat

positions and orientations separately. The intersection point q of Λ and π deter-

mines a point on the outgoing line. For its direction vector, you would reﬂect the

direction u of Λ relative to the normal vector n of the plane. This would refer to a

Euclidean formula such as

nu'

π Λ / π

∧

Figure 13.3: Reﬂection of a line Λ in a (dual) plane π in the conformal model. This is derived

from the reﬂection of a vector u in a normal vector n in the origin, according to the vector space

model (also depicted).

378 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

u → u



= u − 2(u · n)n.

You would then reassemble the position q and the transformed direction u



and

return that as the transformed line, in some data format.

•

Vector Space Model. In the vector space model of geomet ric algebra, we can start

from the same formula, since all quantities belong to it. We have seen in Section 7.1

how this can be reformulated to geometric algebra by introducing the geometric

product, giving

u →−nun= −nu/n

(13.10)

(we introduced the division to waive normalization of n.) This is clearly a versor

product, and the embedding in the geometric algebra of the vector space model gives

us the automatic extension to the reﬂection of any blade in the Euclidean model, not

just a direction vector u.

•

Homogeneous Model. In the homogeneous model we can combine the directional

and locational aspects of the line in one data str ucture, a 2-blade. We can use that

blade to compute the intersection point, but we still need to isolate the direction

vector to perform the reﬂection (by the same formula as the vector space model).

We can then compose the resulting line from the intersection point and the new

reﬂected direction as a resulting 2-blade in the homogeneous model.

•

Conformal Model. In the conformal model, we can completely skip determining the

intersection point. Instead, we extend the reﬂection formula (13.10) from the vector

space model directly from merely working on directions to acting on the whole line,

in the following manner.

We ﬁrst note that the formula also holds in the conformal model, since the vector

space model is contained in it. The direction vector n is now recognized as a dual

plane through the origin, and this is the plane Π of the original problem, as long

as we accept for the moment that it passes through the origin. We write this special

plane as Π

, dually represented by π

= n. We want the vector u to represent the

direction of the line Λ

also passing through the origin. This implies that the line

should be represented as Λ

= o ∧ u ∧∞.

Let us now extend the reﬂection formula of (13.10) to this element Λ

. This is

straightforward, since o and ∞ are invariants of the reﬂection in π

, and the ver-

sor structure of the conformal model does the rest.

o ∧ (−nu/n) ∧∞ = (−n o/n) ∧ (−nu/n) ∧ (−n ∞/n)

= n (o ∧ u ∧∞)/ n.

(We wrote the formula using the grade involution , since there are obviously as

many signs as the grade of Λ

and this w ill help the further generalization below.)

So we now have a formula that reﬂects a line Λ

through the origin in a dual plane

through the origin:

→ π



/π

SECTION 13.5 RIGID BODY MOTIONS 379

Since this formula consists only of geometric products, it is clearly translation

covariant. So moving both to a general position using the Euclidean rigid body

motion V (ﬁrst a rotation then a translation), we get a formula for a general line

Λ=V[Λ

] and a general dual plane π = V[π

]

Λ=V[Λ

] → V[π



/π

] = V[π

] V[



] /V[π

] = π



Λ /π.

Under this motion, the original intersection point o moves to V[o], but the ﬁnal

result holds whether we know the intersection point explicitly or not. So the reﬂec-

tion of a line Λ in a dual plane π in general is

Λ → π



Λ /π,

in all its aspects of location and direction. It can do this without actually computing

the intersection point, and that is an improvement over both the vector space model

and the homogeneous model. (If you really want to compute the intersection point,

the

meet of the plane Π and the line Λ is the ﬂat point Λ ∩ Π=πΛ.)

The result is clearly only the special case for a line of the general reﬂection formula that

reﬂects any directly represented ﬂat space in an arbitrary plane:

X → π



X /π.

(13.11)

You see how much work the nice algebraic structure saves to transfer formulas, as well as

providing clear insights in why they hold, and how to extend them. Classical geometrical

results, typically formulated in the vector space model, are naturally embeddable within

the conformal model. Moreover, we don’t have to spell them all out: with a bit of practice

and conﬁdence, such transfers become one-liners. In the example above, you know that

o is never special, so that (13.11) is the only actual computation to get to the general case.

You may even learn to guess the result (which was clearly possible in the example above

based on the pattern in reﬂection formulas in Table 7.1), and merely verify the correctness

with interactive software (moving its constituents around to check its structure preserva-

tion, and the correctness of weights). That is how we ourselves typically design formulas

for speciﬁc tasks, and the method is justiﬁed by virtue of the structure preservation prop-

erties of the conformal model.

Incidentally, (13.11) is the reﬂection formula used in the motivating example of

Section 1.1.

13.5 RIGID BODY MOTIONS

We have seen in Section 13.2 how the conformal model represents the Euclidean transfor-

mations as versors. Of special interest are the Euclidean rigid body motions, represented

by even versors that can be normalized to rotors. We explore their structure, culminating

in a closed-form logarithm useful for interpolation of rigid body motions.

380 THE CONFORMAL MODEL: OPERATIONAL EUCLIDEAN GEOMETRY CHAPTER 13

13.5.1 ALGEBRAIC PROPERTIES OF TRANSLATIONS

AND ROTATIONS

The rotor T

= exp(−t∞/2) = (1 − t∞/2) has all the desirable properties of a translation

versor. The occurrence of the null vector ∞ makes translation versors combine in an addi-

tive manner in terms of its vector parameter t, since it kills any terms that might contain

the combination of translations:

= (1 − s∞/2) (1 − t∞/2) = 1 − s∞/2 − t∞/2 + s∞t∞/4 = 1 − (s + t)∞/2 = T

s+t

You may contrast this with the much more complicated composition of rotations, which

we saw in Section 7.3. That was essentially the geometric algebra version of the quaternion

product (in 3-D), extended to n-D. It, too, is automatic from the rotor representation

of the rotation, but the result was in essence a n a ddition of arcs on the rotation sphere,

involving severe trigonometry in a coordinate representation.

The algebraic nature of the bivector in the exponent of these rotors is the crucial difference

that makes us experience them so differently geometrically: when it has a negative square,

it generates rotations, which do not commute and involve trigonometry, and when it has

a zero square, it generates translations, which do commute and remain additive. We will

meet the remaining possibility of a positive square later (in Section 16.3, where we show

that they are scalings and involve hyperbolic functions).

The versor structure of the conformal model means that not only elements like ﬂats and

directions transform easily, but so do the versors themselves. A consequence of the prop-

erties of translations is that translations are translation invariant: a translated translation

rotor acts in the same manner as the original rotor, for

] = T

−1

= T

−s

= T

s+t−s

= T

(Note that T denotes the translation rotor, whereas

T[]denotes the translation operator!)

This invariance property is why we feel so free to draw the translation vector anywhere,

attached to any point we like in the same manner. By contrast, rotations are not rotation

invariant:

Jψ

I␾

] = R

Jψ

[I␾]

and therefore the total rotation rotates in the R

Jψ

-rotated plane I, not in the original plane

I. (Again, R denotes the rotation rotor, while

R[]denotes the rotation operator.)

When we translate a rotation rotor R

I␾

= exp(−Iπ/2), by a translation rotor T

, this has

the same effect as shifting the rotation 2-blade by the translation T

I␾

] = R

[I␾]

In 3-D space, this is particularly striking. The rotation 2-blade is the inverse dual of the

rotation axis Λ

also passing through the origin, since Λ

= I

∗

. Originally, the axis

SECTION 13.5 RIGID BODY MOTIONS 381

passes through the origin; after the translation the new axis Λ has become T

[Λ

]. But the

property that the rotation rotor is the exponent of the dual line is covariant, so the new

rotation rotor is simply the exponent of the new dual axis Λ:

3-D rotation around line Λ over angle ␾:R= e

−Λ

−∗

␾/2

= e

∗

␾/2

(Make sure you normalize the axis Λ so that the angle ␾ has the intended meaning.)

In Chapter 7, we showed that the 3-D rotation rotors around the origin were the geo-

metric algebra way of doing quaternions, in what we now recognize was the vector space

model. That had the advantage of embedding quaternions in a real computational frame-

work, but did not add any computational power. In the conformal model, the concept of

a quaternion is greatly extended. In 3-D, the extension encompasses the general rotation

axis for an arbitrary rotation to encode the rotation. (In n-D, it still signiﬁes the 2-blade of

the rotational bivector, though this does then not dualize to a single axis.) This relation-

ship to the rotation axis is very compact and convenient in applications. You have met it

ﬁrst in our motivating example in Section 1.1.

13.5.2 SCREW MOTIONS

A translated rotation is not yet the general rigid body motion, for it lacks a translation

component along the rotation axis. So we would have to supply that separately, to obtain

the general rigid body motion as

I␾

where v is a vector in the plane I (so that v ∧ I = 0), and w is vector perpendicular to it

(so that wI = 0).

Such a decomposition of a rigid body motion gives us a better understanding of what it

does, and we can execute the two parts (translation along the axis and rotation around

the axis) in any order or simultaneously. When we do them in similar amounts to reach

a total resulting rigid body motion, we obtain a screw motion, as depicted in Figure 13.4.

The simultaneous rotation and t ranslation (around and along the spatial axis) are then

related through the pitch of the screw. According to Chasles’ theorem,anarbitraryrigid

body motion can be represented in this manner. Given a general rigid body motion, we

can compute the location and magnitude of the elements of the screw using the confor-

mal model. Perhaps surprisingly, it completely avoids the rather involved trigonometry.

First, assume that we have a general rigid body motion T

I␾

composed of a standard

rotation in a plane I at the origin, followed by a translation. This is the usual way to decom-

pose rigid body motions, which we already encountered in the homogeneous model (in

Section 11.8.5). It corresponds well to the homogeneous coordinate matrices for rigid

body motions. Following Chasles, we attempt to rewrite this rig id body motion as a

displaced rotation around a displaced axis parallel to I

∗

, with its location characterized by