Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour
Подождите немного. Документ загружается.

value arriving at the valve face at this time remains constant at:
Jþ¼V
o
þ g=aH
o
At the valve face V ¼ 0 so that:
Jþ¼V
o
þ g=aH
o
¼ 0 þg=aH
or
H ¼ H
o
aV
o
=g ¼ H
o
H
i
From initial valve closure at time ¼ 0 until time ¼ 2L=a, when a
reflected pressure wave returns to the valve from the reservoir, piezo-
metric level at the valve remains at H
o
þ H
i
. After time ¼ 2L=a,
piezometric level at the valve has fallen to H
o
H
i
. This time 2L=a
from the initiation of the pressure transient is the minimum time
before any ‘relief of pressure’ occurs at the source of the hydraulic
transient. It is sometimes referred to as the ‘critical period’. Remaining
with this simple example, it follows that any closure time which is
2L=a will produce the same maximum head rise as an instantaneous
valve closure. Closure times >2L=a will start to bring benefits of pres-
sure relief with consequent maximum inertial head rise H
i
being
<aV
o
=g. Figure 7.3 shows the position of the wavefront at different
stages as it travels to and fro in the pipeline.
7.4 2L=a < t 3L=a
After this reflected pressure wave has reached the shut valve, head
against the valve has to fall by an amount aV
o
=g below the static
level H
o
in order to ensure that flow remains at rest against the valve
face. As before, this change initially affects only the layer of liquid in
contact with the valve but, as time passes, successive layers of liquid
are influenced as the rarefaction wave travels upstream. Consider the
J Riemann invariant propagating along the C characteristic. Its
value is given by conditions at the valve. Thus:
J¼V g=aH ¼ 0 g=aðH
o
H
i
Þ¼V
o
g=aH
o
The characteristic arrives at the reservoir a total time 3L=a after initial
valve closure. At this stage the entire pipeline liquid column is at rest at
a piezometric level H
o
H
i
. With the reservoir at a level H
o
, conditions
across the inlet to the pipeline are again unstable.
Consider the Riemann invariant value at the reservoir after time
¼ 3L=a. At the reservoir, H ¼ H
o
, therefore:
J¼V g=aH
o
¼ V
o
g=aH
o
or V ¼ V
o
92
Pressure transients in water engineering
7.5 3L=a < t 4L=a
After time 3L=a the velocity at the reservoir end of the pipeline
becomes þV
o
. This is the Jþ invariant value that existed initially
before the valve was shut. So the layer of liquid adjacent to the reservoir
is accelerated back to its original value of V
o
and the piezometric level is
restored to its initial value of H
o
. A short time later the next layer of
liquid is also accelerated to V
o
and its piezometric level increases to
H
o
as a compression wave starts to travel downstream towards the
closed valve.
The Cþ characteristic travelling from the reservoir to the shut valve
has a Jþ invariant value:
Jþ¼V
o
þ g=aH
o
As time passes the pressure wave propagates downstream to reach the
valve after time 4L=a from the initial valve closure. When the pressure
wave reaches the shut valve the entire pipeline is under the reservoir
head H
o
and velocity is everywhere V
o
directed towards the valve.
Conditions are thus precisely the same as existed in the pipeline at
the instant the valve started to close. In the absence of any damping
mechanism, propagation of pressure waves within the pipeline will
continue to be repeated at successive time intervals 4L=a till infinity
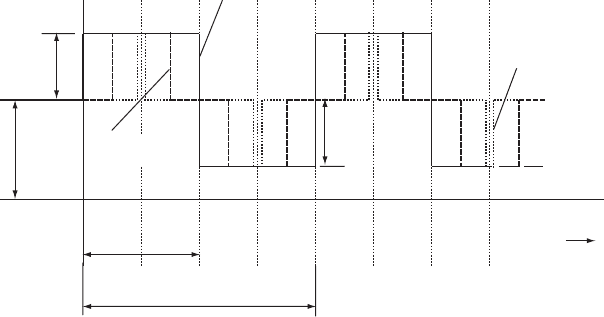
as illustrated in Fig. 7.4. The time interval 4L=a is the period of
elastic oscillations within this pipeline.
In practice there is damping in the shape of pipeline resistance and
‘minor’ losses, as well as entry loss and kinetic energy development at
93
H
o
Period of oscillation = 4L/a
+a
V
o
/
g
–aV
o
/g
Critical time = 2L/a
0Datum L/a 2L/a 3L/a 4L/a 5L/a 6L/a 7L/a
U/s of valve
Close to reservoi
r
Mid-point
of pipeline
Time
Fig. 7.4. Time histories of inertial head in pipeline after valve closure
Valve closure in a simplified system
the inlet to the pipeline from the reservoir. These effects will pro-
gressively erode the transient event until eventually a new steady
flow regime prevails. In theory there will always be some small residual
vestige of the transient with truly steady flow never actually being
reached. In practice the flow may be declared steady when amplitude
of the residual oscillation has become smaller than some selected
finite value.
It will have been noted that compression waves have travelled in
both the positive and negative directions of motion within the pipeline.
The same applies to rarefaction waves. Direction of wave motion, for
example in the positive x direction, does not imply that the wave
produces an increase in pressure.
94
Pressure transients in water engineering
8
Actual pipelines
Whereas Chapter 7 examined an idealised valve closure condition, the
present chapter illustrates some of the differences in behaviour which
can occur between a simplified pipeline and actual systems. Obvious
differences which spring to mind are the effects of pipeline resistance
and losses generally which are a necessary factor if an eventual
almost steady flow condition is to be established. Other aspects
include the possible development of sub-atmospheric pressures and
the radical effect which appearance of gas or vapour cavities can
produce.
8.1 Attenuation
Before proceeding to consider specific examples, some discussion is
appropriate regarding the phenomenon of attenuation which occurs
in pipelines generally but whose existence may not be obviously
apparent except where the pipeline is relatively long. Consider the
circumstance of a valve closed abruptly at the downstream end of a
long pipeline having uniform properties as shown in Fig. 8.1. Steady
flow velocity is V
o
, pipe diameter is D, uniform wave speed is a and
dx=dt ¼a for simplicity. Friction factor f is taken to be constant for
convenience and the effects of pressure change on velocity under
steady flow are ignored. Uniform gradient of piezometric line is S
o
under the original steady flow. Datum for head measurement is taken
to be at the level of the steady flow piezometric line at the valve as
shown in Fig. 8.1.
Head rise H
i
just upstream of the valve when the valve is just closed at
time t
o
¼ 0isaV
o
=g.Atsometimet after closure, the compression wave
front caused by valve closure will have propagated upstream to a point
95
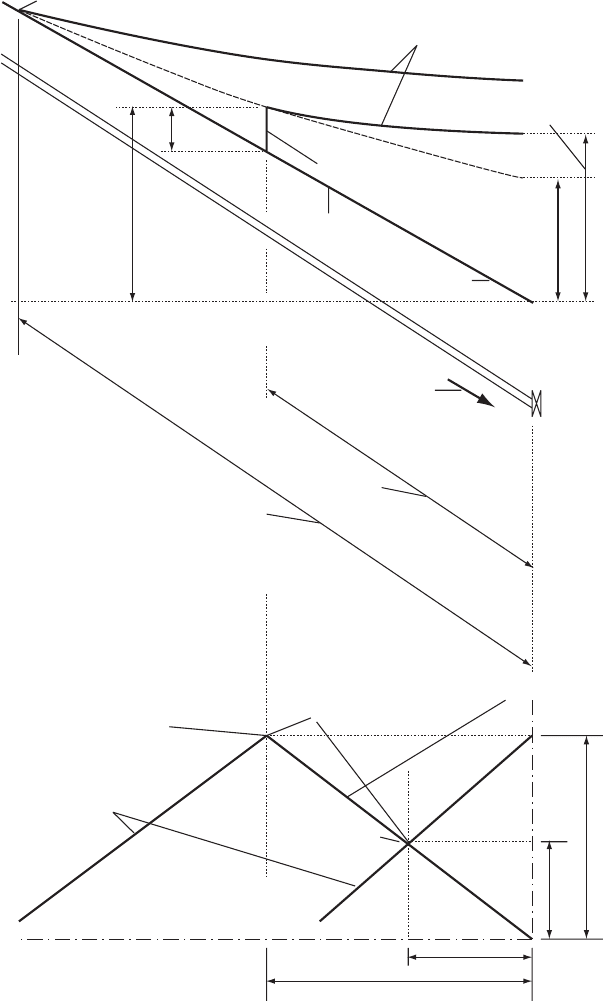
96
V
=
V
o
H
v
H
i
=
a
V
o
/g
H
x
H
X
L
C+ characteristic
Transient piezometric line or
hydraulic gradient
Compression wave
Steady flow
Piezometric line
Gradient = S
o
Horizontal datum
Initial steady
velocity = V
o
C– characteristic
Time t
o
x
t
x/2
t/2
J– = –V
o
– g
Ú
S dt
J+ = V
o
+ gS
o
t
J+ = V
o
+ gS
o
t/2
Fig. 8.1. Attenuating wave front
Pressure transients in water engineering

x ¼ at. If velocity is reduced to zero as the wave passes a point, with
inertial head rise remaining at aV
o
=g then total head downstream of
the wave front will rise continuously at a rate S
o
a.Anyincreasein
head downstream of the wavefront must be accompanied by a continued
flow downstream of the wavefront and so velocity across the front cannot
be entirely reduced to zero and inertial head rise must be <aV
o
=g.A
simple analysis is presented to demonstrate this effect.
With reference to Fig. 8.1, the backward C characteristic starting
from the valve at t
o
will have a quasi-invariant J with a value at
time t of:
J¼V
o
g
ð
S dt ð8:1Þ
where S is the resistance gradient.
8.1.1 Conditions at the wavefront
Just upstream of the wavefront at any time t the Cþ characteristic will
carry the quasi-invariant Jþ value:
Jþ¼V
o
þ g=aS
o
at ¼ V
o
þ gS
o
t ð8:2Þ
At intersection of these opposing paths at time t then:
V ¼ðJþþJÞ=2 ¼
1
2
V
o
þ gS
o
t V
o
g
ð
S dt
¼ g=2
S
o
t
ð
S dt
ð8:3Þ
and
H ¼ðJþJÞ=ð2g=aÞ¼
1
2
a=g
V
o
þ gS
o
t
V
o
g
ð
S dt
¼ aV
o
=g þ a=2
S
o
t þ
ð
S dt
ð8:4Þ
Total head H is made up of the initial steady flow head plus the inertia
head rise H
x
, so that H
x
¼ H S
o
at or H
x
¼ H S
o
x. Then:
H
x
¼ aV
o
=g þ a=2
S
o
t þ
ð
S dt
S
o
at
¼ aV
o
=g þ a=2
ð
S dt S
o
t
ð8:5Þ
97
Actual pipelines
Using the Darcy equation to evaluate head loss due to friction then,
S
o
¼ fV
2
o
=ð2gDÞ and S ¼ fV
2
=ð2gDÞ. Substituting in the expression
for velocity V at the wavefront:
V ¼ f=ð4DÞ
V
2
o
t
ð
V
2
dt
ð8:6Þ
If it is assumed that velocity varies linearly with time along the C
characteristic, then dV=dt ¼ V=t ¼ constant or dt ¼ dV=constant so
that:
ð
V
2
dt ¼ 1=constant
ð
V
2
dV
giving:
V ¼ ft=ð4DÞðV
2
o
V
2
=3Þ
or, solving for V:
V ¼ 6D=ðftÞð
p
f1 þ 3½V
o
ft=ð6DÞ
2
g1Þð8:7Þ
A simpler expression for V can be found by assuming that
3½V
o
ft=ð6DÞ
2
1. Using a series expansion and truncating at the
first term:
V V
2
o
ft=ð2DÞ¼V
2
o
fx=ð2aDÞ¼g=aS
o
x ð8:8Þ
Thus velocity just downstream of the wavefront increases with distance
upstream.
Turning to the equation for H
x
:
H
x
¼ aV
o
=g þ a=2
ð
S dt S
o
t
and making similar substitutions for S and S
o
then:
H
x
¼ a=g½V
o
þ ft=ð4DÞðV
2
=3 V
2
o
Þ
but V ¼ ft=ð4DÞðV
o
V
2
=3Þ so that as expected:
H
x
¼ a=gðV
o
VÞð8:9Þ
This equation demonstrates that the inertial head rise at the front of the
pressure wave diminishes linearly with distance upstream for the
assumed linear variation in V.
98
Pressure transients in water engineering

8.1.2 Conditions when the wave height is of zero amplitude
Returning to the expression for velocity just downstream of the
wavefront,
V ¼ 6D=ðftÞf
p
ð1 þ 3½V
o
ft=ð6DÞ
2
Þ1gð8:7Þ
When the wavefront has been attenuated to the point when V ¼ V
o
then,
V
o
ft=ð6DÞþ1 ¼
p
½1 þ 3ðV
o
ft=ð6DÞÞ
2
Setting y ¼ V
o
ft=ð6DÞ and squaring,
y
2
þ 2y þ 1 ¼ 1 þ 3y
2
rearranging then,
2y
2
2y ¼ 0ory ¼ 1
giving,
V
o
ft=ð6DÞ¼1ort ¼ 6D=ðV
o
fÞ
Since x ¼ at therefore,
x ¼ 6aD=ðV
o
fÞð8:10Þ
The inertial head rise H
x
at the wavefront is given by the expression,
H
x
¼ a=g½V
o
þ ft=ð4DÞðV
2
=3 V
2
o
Þ
When V ¼ V
o
and t ¼ 6D=ðV
o
fÞ then,
H
x
¼ a=g½V
o
þ ft=ð4DÞðV
2
o
=3 V
2
o
Þ
¼ a=gðV
o
ft=ð4DÞ
2
3
V
2
o
Þ
or as expected,
H
x
¼ a=g½V
o
f6D=ð4DfV
o
Þ
2
3
V
2
o
¼0 ð8:11Þ
Confirming that the wave front is of zero height when V ¼ V
o
.
To gauge the magnitude of x consider the following values: V
o
¼ 1 m/s;
f ¼ 0:02; D ¼ 1m and (i) a ¼ 1200 m/s and (ii) a ¼ 300 m/s. Sub-
stituting in equation (8.10), then (i) x ¼ 120 km and (ii) x ¼ 30 km.
Only in very long pipelines is it likely that the wave will be completely
attenuated. In shorter lines significant attenuation can still be
observed.
99
Actual pipelines

8.1.3 Conditions at the closed valve
Total head just downstream of the wavefront at time t is given by:
H ¼ a=gV
o
þ
1
2
S
o
x þ
ð
S dx
¼ a=gV
o
þ fx=ð4gDÞðV
2
o
þ V
2
=3Þ
At the shut valve at time t the Jþ quasi-invariant has the value,
Jþ¼V
o
þ g=aS
o
x=2 g
ð
S dt
where the integral g
Ð
S dt is evaluated between t=2 and t. Making
substitutions for S
o
and S then in terms of velocity V at the wavefront,
Jþ¼V
o
þ ft=ð4DÞðV
2
o
V
2
=12Þð8:12Þ
and head at the closed valve is thus,
H
v
¼ a=gV
o
þ fx=ð4gDÞðV
2
o
V
2
=12Þð8:13Þ
The corresponding head at the wavefront at time t is,
H ¼ a=gV
o
þ fx=ð4gDÞðV
2
o
þ V
2
=3Þ
Comparing the expressions for H
v
and H it can be seen that the head at
the valve lags behind head at the wavefront by an amount,
H H
v
¼ 5fxV
2
=ð48gDÞð8:14Þ
8.1.4 Conditions downstream of a pump or valve
This phenomenon of attenuation is not confined to the pipeline
upstream of a terminal discharge valve: attenuation of a rarefaction
wave also occurs downstream of an in-line valve. In general, such
behaviour is to be anticipated in pipelines connected to a pumping
station following a pumping failure.
8.2 A uniform gravity main
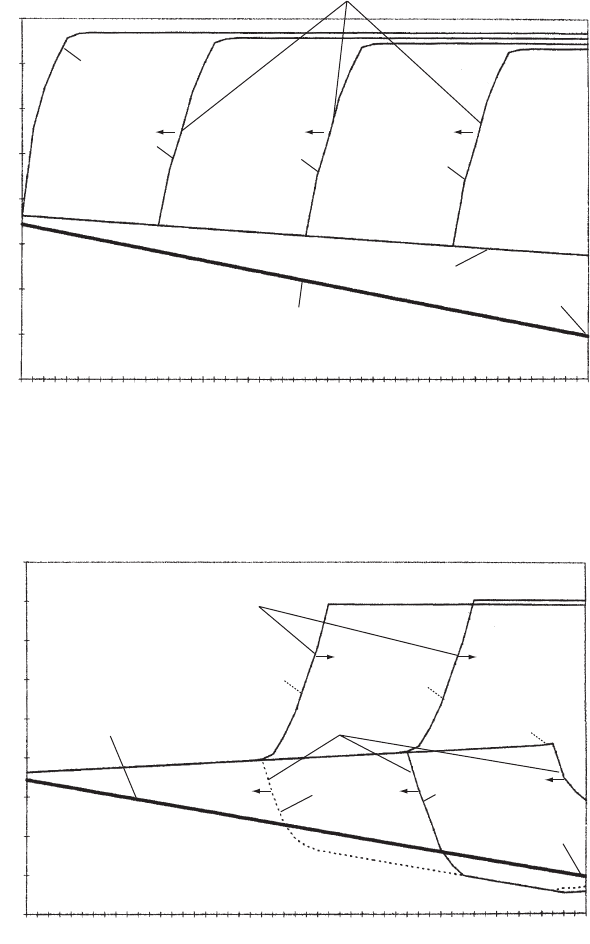
Consider the relatively straightforward gravity main shown in Fig. 8.2a.
The main is of ductile iron (DI) with a length of 19.757 km and nominal
diameter (DN) 450. Pipeline gradient is uniform throughout its length
at 1:398. Water is pumped into the upstream reservoir from a set of
boreholes. From this reservoir, water then flows to a second lower
100
Pressure transients in water engineering
101
0
790.3
1580.6
2370.8
3161.1
3951.4
4741.7
5532
6322.2
7112.5
7902.8
8693.1
9483.4
10 273.6
11 083.9
11 854.2
12 644.5
13 434.8
14 225
15 015.3
15 805.6
16 595.9
17 386.2
18 176.4
18 986.7
19 757
Um Ghafa Water Project
3 s closure of downstream valve
instantaneous hydraulic profiles 4.6 £ t £ 23.01 s
160
140
120
100
80
60
40
20
0
Compression wave
Head (mAD)
t = 4.6 s
t = 0 s
Downstream valve
t = 9.2 s
t = 13.81 s
t = 18.41 s
Steady flow profile
Pipeline profile
Chaina
g
e
(
metres from u
p
stream reservoir
)
Fig. 8.2a. Propagation of compression wave
Closed valve
t = 32.21 s
t = 36.82 s
t = 27.61 s
t = 46.02 s
t = 41.42 s
0
790.3
1580.6
2370.8
3161.1
3951.4
4741.7
5532
6322.2
7112.5
7902.8
8693.1
9483.4
10 273.6
11 083.9
11 854.2
12 644.5
13 434.8
14 225
15 015.3
15 805.6
16 595.9
17 386.2
18 176.4
18 986.7
19 757
Head (mAD)
Um Ghafa Water Project
3 s closure of downstream valve
instantaneous hydraulic profiles
27.61 £ t £ 46.02 s
Rarefaction wave
Rarefaction wave
Pipeline profile
Chaina
g
e
(
metres from u
p
stream reservoir
)
180
160
140
120
100
80
60
40
20
0
Fig. 8.2b. Rarefaction waves following reflection
Actual pipelines
