Ellis,J. Pressure transients in water engineering, A guide to analysis and interpretation of behaviour
Подождите немного. Документ загружается.

The much lower amplitude of oscillation downstream of the valve is
a function of pipeline length and diameter. The longer the pipeline
the greater will be the amplitude but the larger the pipe cross-section
the lower will be the velocity of flow and amplitude of surging
developed.
9.6 Control of transient pressures and estimation of valve
operating time
Essentially, control of hydraulic transient pressures using a valve which
is under operator control is a matter of limiting rates of velocity change.
For a given size and pattern of valve this requires determination of an
appropriate time of closure/opening so as to avoid unacceptable over-
pressure or underpressure.
It has been demonstrated how the retardation of flow in a pipeline
during valve closure is highly non-linear on account of the head loss
relationship of valves. Much of the flow deceleration and the peak
pressure developed will generally occur during this period of high
deceleration. It is always useful for the engineer to be able to make
rapid preliminary estimates of parameters and the necessary valve
closure time is just one of these.
The critical period of a pipeline is 2 L=a and any valve which operates
to open or close in a time 2L=a will create an inertial pressure head
rise ¼a V=g where V is the change in velocity at the valve.
This simple expression ignores the effect of attenuation.
When it comes to valve movements which occur in a time >2L=a
then the effects of wave reflection become significant with a reduced
peak pressure change. Some commentators have introduced a rule of
thumb which separates valve stroke times into rapid or slow movements
with stroke times >20L=a being defined as slow with elastic wave
effects being relatively unimportant.
Provided that valve movement is sufficiently slow that elastic wave
effects are not too important then an initial estimate of valve closure/
opening time can be made using the equation obtained from rigid
column theory. Neglecting pipeline resistance then, inertial head rise
during closure is given by:
H
i
¼L=g dV=dt ð2:2Þ
If an assumption is made regarding closure time and maximum dV=dt
then H
i
can be calculated. If head rise is excessive a more prolonged
closure time is required.
122
Pressure transients in water engineering

For a slow valve closure Fox (1977) developed an equation of the
form:
H
max
=H
o
¼ 1 þ 2K
2
ð1 þ
p
f1 þ 1=K
2
gÞ ð9:1Þ
where K ¼ V
o
L=ð2gH
o
TÞ, H
max
is the maximum head, T is the closure
time, H
o
is the upstream reservoir level relative to discharge level, V
o
is
the initial steady velocity of flow, L is the pipeline length and g is
acceleration due to gravity. A linear reduction of effective valve area
over the stroke time was also assumed.
An alternative approach was described in an ASCE (1975) publica-
tion. This method can be applied to both rapid and slow closure times
and uses the concept of an effective valve closure time. The effective
valve closure time is defined as the time to reduce velocity linearly to
zero which produces the same transient pressure rise as the actual
valve closure time. The actual valve closure will generally produce a
non-linear velocity variation over the closure interval. Each valve
pattern has a different effective closure time as indicated in Table 9.1.
In the case of a gate valve for instance, an actual valve closure time of
100 s will impose a maximum deceleration dV=dt equal to a uniform
rate of deceleration over 39 s. It will be noted that this approach
becomes less viable when resistance effects are high.
In the absence of pipeline resistance the instantaneous head rise
H
max
produced when flow is decelerated in time < 2L=a is aV
o
=g in
Table 9.2. The ratio of head rise H
i
during the closure in effective
time T
eff
, to the instantaneous head rise H
max
, is expressed in units
of 2L=a for different values of a pipeline constant aV
o
=ð2gH
o
Þ where
H
o
is the initial steady flow head at the valve.
Suppose a gate valve is installed at the downstream end of a pipeline
of length 5000 m and initial velocity is 1.0 m/s. Let initial head H
o
be 20 m and wavespeed a ¼ 1000 m/s. Then the pipeline constant ¼
2.548 and critical period ð2L=aÞ¼10:0 s. Instantaneous head
123
Table 9.1. Effective valve closure times
Valve type Effective time as a percentage
of actual valve closure time
Butterfly valve 21
Gate valve 39
Cone valve 49
Globe valve 52
Valve operations
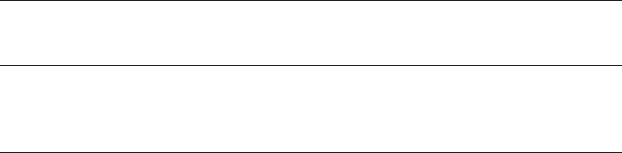
rise ¼1000ð1:0Þ=9:81 ¼ 101:937 mWG. If allowable head rise H
i
is
chosen as say 16 m then H
i
=H
max
0:16 and T
eff
¼ 5:0 10:0 ¼ 50 s.
Since T
eff
is 39% of the closure time for the actual valve then the
required valve closure time is 50=0:39 ¼ 128 s.
124
Table 9.2. H
i
=H
max
as a function of pipeline constant and T
eff
aV
o
=ð2gH
o
Þ T
eff
¼ 5ð2L=aÞ
(seconds)
T
eff
¼ 10ð2L=aÞ
(seconds)
T
eff
¼ 20ð2L=aÞ
(seconds)
0.5—5.0 0.16 0.065 0.028
10.0 0.25 0.082 0.032
40.0 0.56 0.210 0.060
Pressure transients in water engineering
10
Pumps
Pumps are used to move fluids from point to point where insufficient
piezometric head is available to permit gravity flow. Pumping equip-
ment comes in a wide variety of forms to suit a range of different
functions. The potential for pressure transients to be initiated by each
type of pump is dependent upon the characteristics of the pump. The
majority of pumpsets in service initiate hydraulic transient events
when starting or stopping while other types of pump are themselves
incapable of initiating such events. Some designs of pumping plant
create transient behaviour as a part of their operation and in one
case the pump only functions by creating a hydraulic transient and
using its properties to lift water. In any discussion of hydraulic transients
it is therefore worthwhile to spend some time considering the types of
pump available and their characteristics as these will have a bearing
upon the nature of transient events developed and also on the types
of surge protection equipment appropriate in each instance.
10.1 Types of pump
The majority of pumps used in the water and sewerage industries can be
classified in a number of ways but from a transient standpoint pumps
may be grouped as discussed below.
10.1.1 Pumps which produce transient behaviour only when
changing their mode of operation — that is, starting, stopping
or changing speed
This category contains the majority of pumps used in water and sewerage
and includes the large family of centrifugal pumps or turbine pumps and
125
such positive displacement types as screw pumps where water is trapped in
spaces between the rotating element and the pump casing and is forced
through the pump to the discharge side.
10.1.2 Pumps which generate surge effects as a by-product of their
operation
This group includes reciprocating pumps in which a piston moves in
alternating directions within a close-fitting cylinder. While moving in
one direction the piston produces a partial vacuum into which water
flows through an intake port. As piston direction reverses water is
pressurised and forced out via an outlet port. The discharge from this
type of pump will tend to be pulsating to some extent. This second
group also includes the pneumatic ejector in which small sewage
flows are periodically discharged into a rising main using compressed
air and producing a transient event in that main.
10.1.3 Pumps which produce transient events in order to fulfil their
function
The hydraulic ram is an example of this third category. In this device
the flow of liquid in a supply pipe is arrested quickly by closing a
waste or impulse valve and producing a transient pressure rise upstream
of this valve. A delivery valve opens and the flow enters the air chamber
under the increased pressure. The increase in pressure allows flow to be
lifted to a header tank. Once the flow in the supply pipe starts to
reverse, the delivery valve shuts and the waste valve reopens to allow
a new cycle of operation to begin.
10.1.4 Pumps which do not by themselves produce surge effects
This group includes devices such as the jet pump where a supply of
liquid under pressure is forced through a nozzle or jet to entrain the
liquid to be pumped. An exchange of momentum occurs between the
high-velocity jet of ‘motive’ liquid and the low-velocity liquid to be
pumped. The combined flow exits via a diffuser.
10.2 Turbine pumps
Turbine pumps are characterised by one or more impellers equipped
with vanes, which rotate in a pump casing. These pumps are called
radial flow, mixed flow or axial flow pumps depending upon the
126
Pressure transients in water engineering
primary direction of flow through the impellers. Alternative terms also
used are centrifugal for radial pumps and propeller for axial pumps. The
mixed-flow types are intermediate forms between the purely radial and
axial types and are also called semi-axial, Francis or in some cases
diagonal pumps. Impeller forms for each type are illustrated in Fig. 10.1.
Since their use is so widespread, it is not surprising to find that the
majority of pressure transient analyses involves these pumps.
Turbine pumps constitute the largest group of pumps in use nowadays
for transfer of water and sewage. These will be primarily electrically driven
but in some circumstances diesel or other engines may be used.
10.2.1 Centrifugal or radial flow pumps
In radial flow pumps, water enters at the centre of the casing and flows
radially outwards being accelerated by an impeller rotating with angular
127
N
s
= 20–35
Radial
N
s
= 35–60
Radial
N
s
= 60–90
Francis/semi-axial/diagonal
N
s
= 90–120
Francis/semi-axial or diagonal
N
s
= 160–300
Axial/propeller
N
s
= 120–160
Mixed flow
Fig. 10.1. Impeller types
Pumps
velocity ! rad/s. Water leaving at the periphery of the impeller is slowed
by the casing and a proportion of this energy is converted to potential
energy or pressure. This conversion may be achieved by the shape of
the casing itself as in a ‘volute’ pump or by internal diffusers or guide
vanes.
10.2.2 Mixed or semi-axial flow pumps
Pressure head is developed partly by centrifugal action and partly
through lifting action of vanes on the liquid. Flow enters axially and
discharge is through both centrifugal and radial motion. This category
of unit is often found within installations operating at low head and
requiring high-volume output.
10.2.3 Axial flow or propeller pumps
Pumping head is obtained principally through lifting action of vanes on
liquid. A single inlet impeller is used and flow enters axially and
discharges almost axially. Diffusion vanes may be installed on the exit
line to reduce swirl produced by the rotating propeller.
10.3 Turbine pump performance curves
In centrifugal pumps the pressure or the head H
p
developed across the
pump is proportional to the kinetic energy of flow at exit from the impeller
V
2
=ð2gÞ and velocity V is proportional to the speed of rotation ! and
diameter D. It follows that for a family of pumps of varying diameter:
H
p
!
2
D
2
and Q !D
3
ð10:1Þ
Output power Pr ¼ QH
p
, where ¼ g is the specific weight of
liquid flowing, is therefore given by:
Pr !D
3
!
2
D
2
or Pr !
3
D
5
ð10:2Þ
If speed, discharge and head developed are known for a single pump
then
Q=! ¼ constant; H
p
=ð!
2
D
2
Þ¼constant and Q=ð!D
3
Þ¼constant
Eliminating D from the above relationships:
!
p
ðQÞ=H
3=4
p
¼ constant ¼ !s ð10:3aÞ
where !s is called the specific speed.
128
Pressure transients in water engineering
Since specific speed is not dimensionless it will have different numer-
ical values depending upon the system of units employed. All identically
shaped pumps have the same specific speed irrespective of their size.
The values used in calculating the specific speed of a pump are those
at the point of maximum efficiency. Rotational speed may be defined
as N rev/min where N ¼ 60!=ð2Þ, H
p
may be metres and Q m
3
/s.
Specific speed N
s
in rev/min is then:
N
s
¼ N
p
ðQÞ=H
3=4
p
ð10:3bÞ
From experience it is usually possible to estimate the impeller shape
which will give best results for a given speed, flow rate and delivery
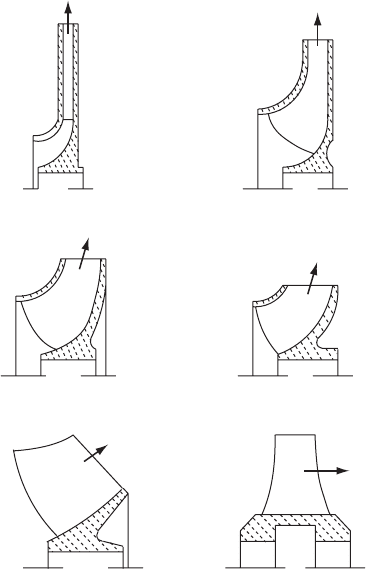
head. Figure 10.2 shows the relationship between pump efficiency
and specific speed for N
s
expressed in units rpm
p
ðm
3
=sÞ=m
3=4
.
When flow is small and head is relatively high, specific speed is small,
favouring a radial type of impeller. For large flow rates and low head
conditions, specific speed is high and the axial type is most suitable.
When pumping clean water, treated effluent or sewage that has been
129
Q = 63.1 litre/s
Q = 31.5 litre/s
Q = 12.6 litre/s
Q = 6.3 litre/s
10 20 30 40 50 60 70 80 90 100 200 30
0
100
90
80
70
60
50
40
Efficiency (%)
Q > 631 litre/s
Q
>
=
631 litre/s
Q = 315 litre/s
Specific speed (rpm ÷(m
3
/s)/m
3/4
)
Fig. 10.2. Specific speed plotted against efficiency
Pumps
passed through fine screens, radial pumps can be used with efficiencies
reaching 90%.
Other considerations other than pumping efficiency can be impor-
tant, for example in sewage pumping. When required to pass solid
material, the impeller shape can be modified to avoid choking and/or
to disintegrate matter present in the sewage. Some efficiency is
sacrificed and such pumps may have peak efficiencies in the 50—60%
range. Sewage pumps will usually operate at relatively low speed,
typically not greater than 960 rpm. This compares with speed of a
clean water pump which will usually be 1460 rpm and upwards. An
unchokable pump may be classified according to the size of solid
object which it can pass, with the normal maximum being specified
as 100 mm. For very small flows, such as from isolated properties, it is
not practical to make a centrifugal pump capable of handling the
130
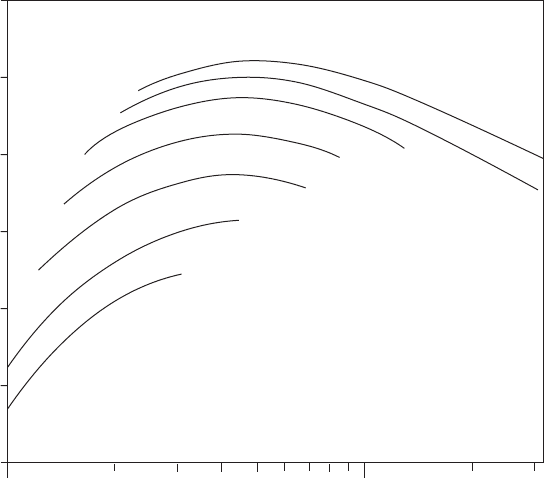
(c)
H, P
H, P
H–Q
P–Q
P–Q
P–Q
P–Q
H–Q
H–Q
H–Q
H, P
H, P
(d)
QQ
(a) (b)
QQ
Fig. 10.3. Performance curve forms: (a) unstable, overloading; (b) stable, non-
overloading; (c) high shut-off head, flat power curve; (d) high shut-off head, high
shut-off power
Pressure transients in water engineering

small volumes while retaining the ability to pass 100 mm diameter
solids. Other forms of pumping equipment must therefore be used.
For a single member of that family which is part of an hydraulic
transient analysis, diameter D is constant and so the relationships
10.1, 10.2 and 10.3 can be reduced to:
Q !;H
p
!
2
and Pr !
3
or in terms of speed N expressed in rpm:
H
p
N
2
; Q N and Pr N
3
Behaviour of a typical centrifugal pump is usually described by perfor-
mance curves relating H
p
, Q, Pr and N. The shape of the curves is
related to the form of impeller and specific speed. Typical shapes of
performance curves are illustrated in Fig. 10.3. Where it is necessary
to deliver a range of flows with only a relatively modest variation in
head then a flat curve relating H
p
and Q is more suitable. If pumping
head varies considerably and it is desired to deliver an almost steady
flow then a steep H
p
—Q curve is more attractive.
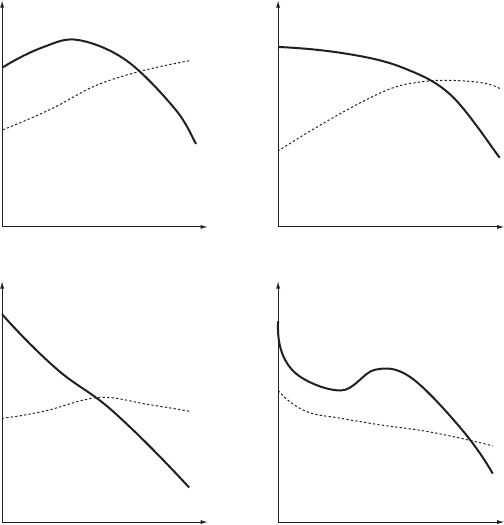
When a pump is starting/stopping, its speed varies continuously and a
family of performance curves is produced covering the speed range
(Fig. 10.4). Similar points on different curves will display the same
relationship between the variables so that plotting H
p
=N
2
against Q=N
131
H
p
Q
H
p
–Q curve at design speed
Duty point
Speed N reducing
H
p
–Q curves at reduced speed
Fig. 10.4. H—Q performance curves for changing speed N
Pumps
