Емельянов В.Ю. Методы моделирования стохастических систем управления

Подождите немного. Документ загружается.

P((t

) = u

"0"

) = P((t

) = u

"1"

) = 0,5. (3.24)

Моменты t

выбираются с шагом t, достаточно большим, чтобы обес-

печивать независимость последовательных значений сигналов

(t

),(t

i+1

),… В разряды регистра заносятся N последовательных значе-

ний . Таким образом в регистре формируется N-разрядное двоичное число:

=

-1

+

-2

+…+

-N

10 

Число  имеет 2

значений, вероятность каждого из которых вследствие

(3.24) равна

. Таким образом, получаемые числа  имеют равномер-

ный дискретный закон распределения в интервале

 

2110 ;

. Если при-

нять N достаточно большим, можно считать получаемый закон распределе-

ния непрерывным:

 













.10

припри

при

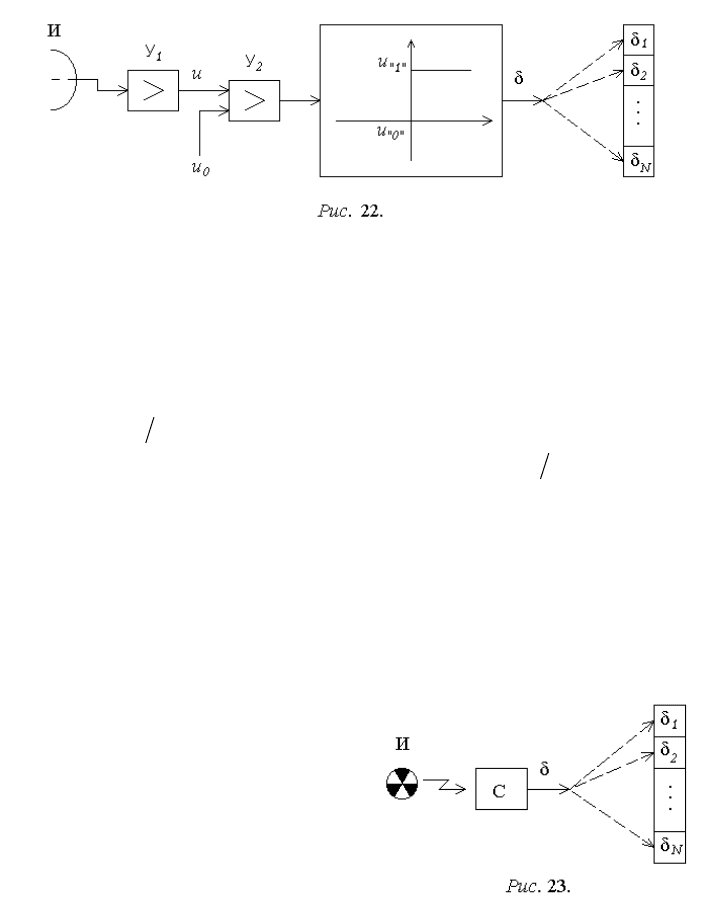
Недостаток такого генератора состоит в нестабильности характеристик

используемых флуктуационных шумов и необходимости периодической

точной подстройки уровня u

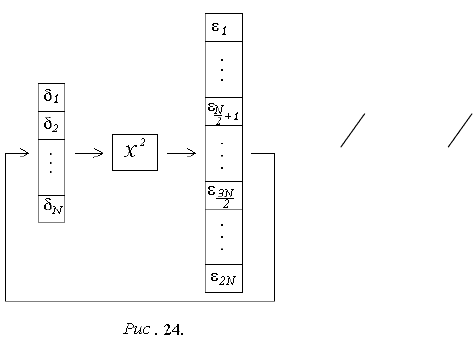
От указанного недостатка сво-

боден генератор, использующий

излучение радиоактивного элемента

И (рис. 23). Здесь в зависимости от

количества частиц, регистрируемых

счетчиком С на непересекающихся

интервалах времени t

ся выходной сигнал: при четном

n(t

) формируется уровень логиче-

ского нуля, при нечетном - уровень логической единицы. Для этого доста-

точно использовать бит, содержащийся в младшем разряде выходного реги-

стра счетчика. Очевидно, оба уровня оказываются равновероятными с высо-

кой достоверностью. В остальном построение генератора аналогично преды-

дущему варианту. Недостаток такого генератора связан с очевидными огра-

ничениями его применения.

Помимо рассмотренных, существует еще ряд аппаратно реализуемых

вариантов построения генераторов, также использующих "естественную"

случайность, присущую реальным физическим процессам, которая и явля-

ется их основным и весьма важным достоинством. Общие недостатки таких

генераторов - сложность технической реализации и невозможность повторе-

ния наблюдаемых реализаций случайных последовательностей.

Другой подход к построению генераторов случайных чисел заключается

в аппаратной или программной реализации некоторого рекуррентного соот-

ношения, обеспечивающего получение средних характеристик, аналогичных

характеристикам случайной последовательности.

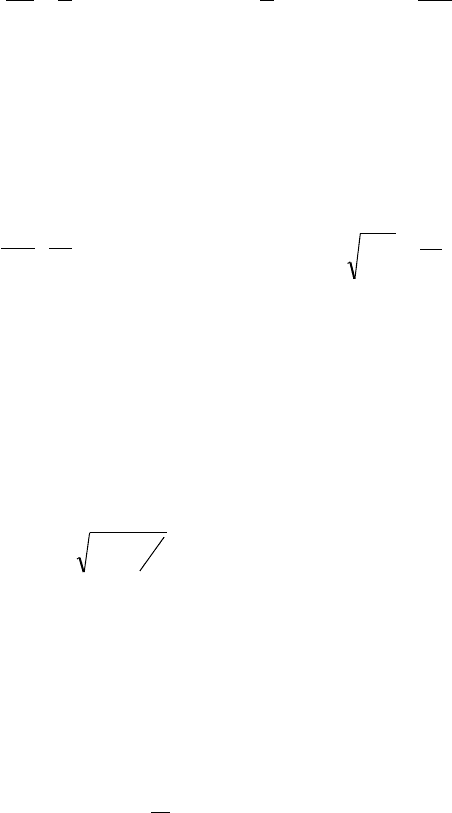
Примером аппаратной реализации такого подхода является генератор на

регистрах, использующий метод Неймана (рис. 24). Пусть в N-разрядном

регистре содержится некоторое число 

=

-1

+ +

-2

+…+

-N

, где N - четное.

После возведения этого числа в квад-

рат для размещения результата в

общем случае потребовалось бы 2N

разрядов. Новое число формируется

из N средних разрядов результата с



по

Последовательность случайных

чисел формируется путем цикличе-

ского повторения такой процедуры.

Впоследствии был разработан ряд

модификаций такого генератора [23],

достаточно точно обеспечивающих

равномерное распределение в ин-

тервале [0; 1].

Генератор рассмотренного типа

представляет собой детерминированный конечный автономный автомат

F=Z,Y,,, объем внутреннего алфавита которого составляет 2

. После-

довательность выходных сигналов такого автомата заведомо не является слу-

чайной. Числовые последовательности, формируемые на основе описанного

подхода, называются псевдослучайными и имеют следующие особенности:

1. Цикличность - длительность цикла детерминированного автономного

автомата не превышает количества элементов внутреннего алфавита.

2. Регулярность - генерируемая последовательность жестко зависит от

начальной установки.

3. Возможность получения "вырожденной" последовательности - на-

пример, если на очередном шаге получено значение =0, все последующие

значения также будут нулями.

Указанные особенности являются одновременно и основными недос-

татками генераторов псевдослучайных чисел. Однако при достаточно боль-

ших N и удачных схемных решениях удается получить псевдослучайные по-

следовательности длиной до 10

чисел, в которых указанные недостатки про-

являются незначительно.

Достоинства генераторов псевдослучайных чисел - сравнительная про-

стота реализации и возможность повторения полученных последовательно-

стей.

3.5.2. Программные способы построения генераторов случайных чисел

Программные генераторы случайных чисел обеспечивают получение

только псевдослучайных последовательностей со всеми указанными выше

недостатками. Общий принцип построения программных генераторов со-

стоит в том, что на первом этапе имитируется равномерный закон распреде-

ления в интервале [0; 1], а затем полученная последовательность преобразу-

ется для обеспечения требуемых характеристик. Рассмотрим ряд способов

построения программных генераторов.

1. Получение равномерного закона в интервале [0; 1] обеспечивается

на основе использования рекуррентных соотношений различного вида, на-

пример:

 

mod





, i=1,2,...,

где a,b - положительные числа, m=2

, l - разрядность представления целого

числа в ЦВМ. Генераторы, или датчики, случайных чисел с равномерным

законом распределения имеются в виде встроенных процедур во всех языках

программирования, позволяющих решать вычислительные задачи. Сущест-

вует ряд способов проверки качества таких генераторов [23, 37]. Но прежде

всего при выборе программных средств для статистического моделирования

следует обратить внимание на способ начальной установки генератора и

возможности ее изменения.

2. Метод обратных функций, обеспечивающий получение заданного за-

кона распределения, основан на использовании известного результата теории

вероятностей: независимо от вида непрерывного закона распределения при

известных его ПРВ f(x) и ФРВ F(x) случайная величина

   

xFduufR







(3.25)

распределена по равномерному закону в интервале [0; 1].

Действительно, в соответствии с (3.25) значения x и R связаны взаимно

однозначной зависимостью. Поэтому для любых A и B

 

10  BА

     





duufbxaPBRАP

   

ABduufduuf







, (3.26)

что является свойством равномерного закона распределения.

Если удается получить аналитическое выражение для функции F

-1

(R),

обратной ФРВ F(x), процедура генерирования случайных чисел x

будет

выглядеть следующим образом:

а) с помощью стандартного генератора получают равномерно распре-

деленные в интервале [0; 1] числа 

;

б) числа x

получают по формуле x

-1

(

Например, для экспоненциального закона распределения (x>0)

f(x)=e

-x

, F(x)=1-e

-x

   

iii

Fx 







1ln

Рассмотренный способ позволяет получать любой непрерывный закон

распределения, если только существует аналитическое выражение для F(x)

и может быть получена в аналитическом виде обратная функция.

3. Для нормального закона распределения аналитического выражения

для ФРВ не существует. Простейший способ получения случайных чисел с

нормальным законом распределения основан на центральной пр едельной

теореме. В соответствии с ней среднее арифметическое n равномерно рас-

пределенных в интервале [0; 1] случайных чисел имеет асимптотически

нормальный закон распределения с математическим ожиданием 0,5 и дис-

персией

     

duu

duufu

5,0











На практике это в достаточной степени подтверждается при n=12.

Поэтому процедура получения нормального закона выглядит следую-

щим образом:

а) с помощью стандартного генератора получают 12 равномерно рас-

пределенных в интервале [0; 1] чисел 

;

б) числа x

со стандартизованным нормальным законом распределения

получают по формуле, являющейся следствием (3.5):

65,0































Для сокращения трудоемкости этот способ иногда применяют с n=6.

Отметим, что рассмотренным способом не обеспечивается свойствен-

ный нормальному закону неограниченный диапазон распределения генери-

руемых чисел.

От указанного недостатка свободна, например, следующая процедура:

а) с помощью стандартного генератора получают два равномерно рас-

пределенных в интервале [0; 1] числа 

и 

i+1

;

б) вычисляют V

=2

–1, V

=2

i+1

–1, s=V

;

в) если

1s

, повторяют пункты а) и б);

г) вычисляют

ln2



и получают два распределенных по стан-

дартизованному нормальному закону числа x

r, x

j+1

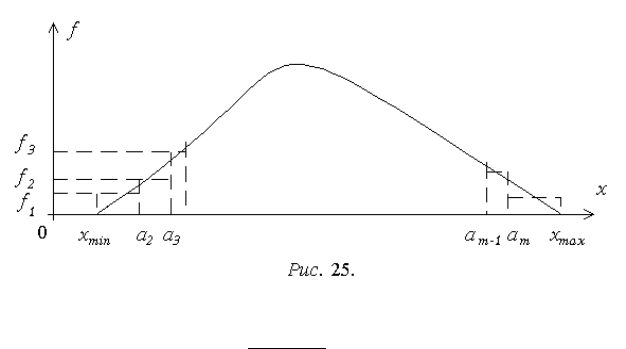
4. Для произвольных законов распределения, не допускающих аналити-

ческого получения ФРВ, существует универсальный способ (рис. 25), осно-

ванный на кусочной аппроксимации функции ПРВ. Рассмотрим его на при-

мере усеченного закона распределения, когда f(x)=0 за пределами отрезка

min

; x

max

]. Разобьем указанный отрезок на m=2

, (l - целое) интервалов

таким образом, чтобы вероятность попадания x в каждый интервал была

одинаковой:

 

axaPp

jjj





, j=1,2,...m; a

min

, a

m+1

max

В пределах каждого интервала ПРВ аппроксимируется константой:





1

, j=1,2,...m.

Процедура формирования случайных чисел в соответствии с заданной

ПРФ f(x) выглядит следующим образом:

а) с помощью стандартного генератора получают равномерно распре-

деленное в интервале [0; 1] число 

2i-1

;

б) по первым l разрядам 

2i-1

выбирают номер интервала j;

в) получают следующее значение 

;

г) значение x

вычисляют по формуле x

+(a

j+1

-a

)

Рассмотренный способ обеспечивает получение псевдослучайных ч и-

сел с любыми непрерывными или кусочно-непрерывными законами рас-

пределения, в том числе задаваемыми таблично. Его недостатками являются

сравнительно большие объемы подготовительной работы и используемой

оперативной памяти ЭВМ.

5. Отметим другой универсальный способ построения генератора слу-

чайных чисел с заданной ПРВ усеченного закона распределения (рис. 26),

также часто называемый в литературе методом Неймана. Он предусматрива-

ет следующую процедуру обеспечения заданной ПРВ f(x):

а) с помощью стандартного генератора получают пары равномерно

распределенных в интервале [0; 1] чисел 

2i-1

и 

;

б) выполняют их преобразование:

min

+(x

max

–x

min

)

2i-1

, y

max



; (3.27)

в) в качестве генерируемых значений случайной величины x выбирают

значения x

из тех пар x

и y

, для которых выполняется неравенство

 

xfy 

. (3.28)

Покажем справедливость данного способа, применительно к его реали-

зации на ЦВМ. Будем рассматривать для каждого x

элементарную полосу

шириной , в пределы которой с учетом разрядности используемой ЦВМ

другие значения x попасть не смогут. Величина  достаточно мала, чтобы

при законе распределения с ПРВ f(x) вероятность x=x

можно было счи-

тать пропорциональной f(x

). С учетом свойства равномерного закона (3.26)

нетрудно убедиться, что это и будет обеспечиваться при достаточно большой

длине генерируемой последовательности на основе условия (3.28).

Преимущество рассмотренного способа - минимальный объем подго-

товительной работы. Тем не менее он не получил широкого практического

применения из-за низкого быстродействия, обусловленного большой долей

“безрезультатных” вычислений. Применение этого способа можно пореко-

мендовать только для более сложных задач моделирования случайных векто-

ров со статистически зависимыми составляющими, которые будут рассмот-

рены в подразд. 3.9.

6. Для формирования случайных чисел с дискретным законом распр е-

деления используется выражаемое соотношением (3.26) свойство непрерыв-

ного равномерного закона.

Пусть требуется построить генератор дискретной случайной величины

Z, имеющей n

возможных значений z

,…,z

. Закон распределения Z

задается в табличном виде или в виде ряда













ppp

zzz



, где p

=P(Z

= z

), причем







. (3.29)

Соотношение (3.26) позволяет установить соответствие между значе-

ниями непрерывной случайной величины  с равномерным законом рас-

пределения в интервале [0; 1] и значениями дискретной случайной величи-

ны Z следующим образом. Разобьем интервал [0; 1] на n непересекающихся

последовательных отрезков 

, выбрав длину каждого из них равной a

–a

. В соответствии с (3.29) эти отрезки полностью займут весь интервал [0;

1] (рис. 27), причем их границы будут определяться соотношениями:





Теперь достаточно принять Z=z

, если значение случайной величины 

попадает в пределы отрезка [a

j-1

; a

]. Соответствующая процедура получе-

ния дискретного закона распределения выглядит следующим образом:

а) с помощью стандартного генератора получают равномерно распре-

деленное в интервале [0; 1] число 

;

б) определяют номер j отрезка 

из условия

jij

aa 

1

;

в) случайной величине Z присваивают значение z

В заключение отметим, что широкий набор разработанных к настояще-

му времени способов построения генераторов случайных чисел, безусловно,

не исчерпывается рассмотренным перечнем. Так для получения нормально-

го и ряда других важных для практических приложений законов распределе-

ния в литературе [1, 7, 17, 23, 28, 36, 41, 44, 46] предлагается большой выбор

различающихся по точности и трудоемкости специальных способов.

3.6. Методы восстановления закона распределения по результатам

статистического моделирования

Закон распределения реализаций случайной величины x

,…,x

, со-

ставляющих выборку некоторой длины n, называется выборочным, или ста-

тистическим. Получение выборочной ФРВ F

(x) или ПРВ

 

xdF





является одной из основных задач обработки результатов

статистического моделирования. Возможны два варианта постановки такой

задачи:

1. Вид закона распределения (чаще всего - аналитическое выражение для

ПРВ) известен и требуется определить только его параметры. При такой по-

становке задачи применяются параметрические методы восстановления

закона распределения.

2. Вид закона распределения неизвестен. В таком случае для его получе-

ния применяются непараметрические методы.

3.6.1. Параметрические методы восстановления закона распределения

Если известно или считается известным аналитическое выражение для

ПРВ, она рассматривается как функция f(x,A), где A=(a

,…,a

) - вектор

неизвестных параметров.

В соответствии с методом наибольшего правдоподобия вводится

функция правдоподобия

   





xfxxxL

,,,...,, АА

где x

- реализации случайной величины x, составляющие выборку.

В качестве оценок параметров a

выбираются значения, доставляющие

локальный максимум функции правдоподобия. Для этого в соответствии с

необходимым условием достижения локального экстремума составляются m

уравнений:

 

,,...,,





xxxL

, j=1,2,...,m.

Решение полученной системы m уравнений с m неизвестными дает век-

тор оценок искомых параметров A

=(a

,…,a

Пример: f(x)=f(x,)=e

-x

0x

, A=(), m=1,

 









exxxL

,,...,,

 









xnexxxL

lnlnln ,,...,, А

 

,,...,,















nxxxL























В соответствии с методом моментов уравнения для оценок неизвестных

параметров образуются приравниванием выборочных начальных м оментов

распределения

 





аналогичным моментам распределения генеральной совокупности

 

   







 dxxfxaa

A,,...,,

Количество составляемых уравнений соответствует количеству неиз-

вестных параметров:

 

aa ,...,,

aM=m

, l=1,2,...,m.

Пример: f(x)=f(x,)=e

-x

0x

, A=(), m=1,

 





 































xedxexM