Ежков В.В., Зарудский Г.К., Зуев Э.Н. и др. Электрические системы и сети в примерах и иллюстрациях

Подождите немного. Документ загружается.

агрегата 100 МВт, либо один агрегат 100 МВт и один агрегат 150

МВт. Другие варианты по условиям задачи неприемлемы. Опре-

делим приведенные затраты, соответствующие этим значениям:

АР. = 100 МВт, Z<')=3i(APi)=0,214.100-350.10^ =

7490

тыс.

руб/год. Остальные значения приведены в табл. 8.12.

Таблица 8.12. Допустимые варианты ввода мощности в первый год

Суммарная генера-

ция Р<« МВт

850

900 950 1000

ДР,. МВт 100 150

200 250

тыс. руб/год 7490 11235 U980 18725

На первом шаге оптимизации принимаемых решений пока

нет. Рассматриваются все допустимые варианты. Перейдем к рас-

смотрению второго года.

При разработке вариантов на второй год необходимо учиты-

вать ограничения

P<')=750+APi5=826 МВт;

Р<^)=750+АР,+АР25=859 МВт;

АРг = 100

-I-150 «2

<250 МВт.

Для этого года целевую функцию вычисляем так:

Z<^)=min

{32(AP2)

+ Z<'>}=min{32(AP2)+3i (АР^)}.

Здесь 3i(APi)=0,214^i:

З2

(АР2)=(0,12

К^

0,094 ЛГг) (1

+ 0,08)"

0,198 К^,.

Покажем вычисление для варианта развития, когда APi = 150

МВт, а АР2=0:

2«=32(0)+3I(150)=0 +

11235

= 11235

ТЫС.

руб/год.

В табл. 8.13 приведены возможные варианты развития на

второй год расчетного периода, а в табл. 8.14 — условно-оп-

тимальные решения для второго года, найденные в результате

анализа табл. 8.13.

Таблица 8.13. Возможиые варнавты развитая иа второй год

Сумма1»а1

гевермща

^>®.MBт

МВт МВт

МВт

зд/^.).

тыс, руб/год тыс. руб/год

Z®.

тыс. руб/год

МВт

900 150 150 0 11235 0

11235 0

930

200 100

100

7490

6930 14420

100

930

200

149») 0

14980

230

продолжение табл. 8.13

Суммарная

генерация

ри МВт

liPf.

МВт

ИРг.

МВт

тыс. руб/год

тыс. руб/год тыс. руб/год

Ai-j'.

МВт

250

100 150 7490 10395

17885

1000

150 100 11235 6930

18165

150

250

0 18725 0

18725

Покажем, каким образом из возможных вариантов приращения

мощности выбирают условно-оптимальное решение. Для приме-

ра рассмотрим выбор оптимального решения при условии, что

суммарная генерирующая мощность во второй год составляет

1000 МВт. Как видно из табл. 8.13, суммарное приращение

мощности APJ+АР2 = 250 МВТ. Такое значение суммар-

ного приращения может быть получено различными способами.

Так, если АР^ = 100 МВт, а АР2= 150 МВт, то суммарные приве-

денные затраты составят

17 885

тыс. руб/год. Если же принять

APi =

150

МВт, а

АР2

100

МВТ, ТО приведенные затраты ока-

жутся выше и составят 18 165 тыс. руб/год. В третьем из возмож-

ных вариантов они еще выше и составят

18 725

тыс. руб/год.

Поэтому для суммарной генерирующей мощности 1000

МВт в качестве условно-оптимального решения принято

АРГ = 150 МВт.

Таблица 8.14. Условио-оотямальиые решевм для второго года

Суммарная генера- 900 950 1000

рация Р®, МВт

APY". МВт

100 150

Z®, тыс. руб/год

И 235 14420

17885

Рассмотрим ввод генерирующей мощности для третьего года.

В этот год требуемая генерируемая мощность должна быть не

меньше 894 МВт (см. табл. 111). Кроме того, должны быть

вьшолнены ограничения:

Р(^>=750-ЬАР^^>>895 МВт;

Р =750-ь АР =750-ь

АР -J-АРз

894

М Вт;

АРз =

100 п, -J-150 «2

<250 МВт.

Затраты на ввод мощности в третий год:

Зз

(АРз)=(0,12

ЛГз -t- 0,094 ЛГз) (1

+ 0,08)-^=0,183 К^.

При определении затрат на ввод генерирующей мощности

используем уже найденные для второго года условно-оптималь-

ные решения (см. табл. 8.14)

г<^)=т1п{Зз(АРз)-|-г<^)}.

231

в табл. 8.15 приведены возможные варианты ввода мощности

в третий год, в табл. 8.16 — полученные на ее основе усло-

вно-оптимальные решения для этого года.

Таблица 8.15. Возможяые вармшты ввода мощвосп в третвй год

Суммарная

геверация

МВт

А/»".

МВт

А/»,

МВт

Д7>«

МВт

тыа руб/гсщ

Z®.

тыс. руб/год

^р)

тыс. руб/год МВт

900

150

150 0

11235

950

200 0 200 0

14420

1000 250 0

100

250

150

6405

17885

11235

17885

17640 100

Таблица 8.16. Условяо-оитильиые решеявя

для третьего года

900 950 1000

да«

7»®.

МВт

МВт 0

0 100

Z"', тыс. руб/год 11235 14420

17640

Вычисления для четвертого года аналогичны приведенным

выше вычислениям для третьего года. В этот год суммарная

генерирующая мощность должна быть не меньше 929 МВт (см.

табл. 8.11). При разработке вариантов ввода мощности нужно

учитывать ограничения:

P®=750+APg>>894 Мвт;

Р<^>=750+АР<^+АР4>929 МВТ;

АР4= 100«i + 150И2<250 МВТ.

Затраты на ввод генерирующей мощности:

Зз (АР4)=(0.12 +0,094 К^)

+ 0,08) - '=0,1699 К^

В табл. 8.17 приведены возможные варианты ввода мощности

в четвертый год, а в табл. 8.18 — полученные на ее основе

условно-оптимальные решения для этого года.

Пятый год является последним для расчетного периода, по-

этому он может планироваться так, чтобы была получена на-

ибольшая выгода. Как видно из табл. 8.11, в пятый год суммар-

ная генерирующая мощность должна быть не меньше 966 МВт.

Очевцдно, что для получения наибольшей выгоды нужно вы-

232

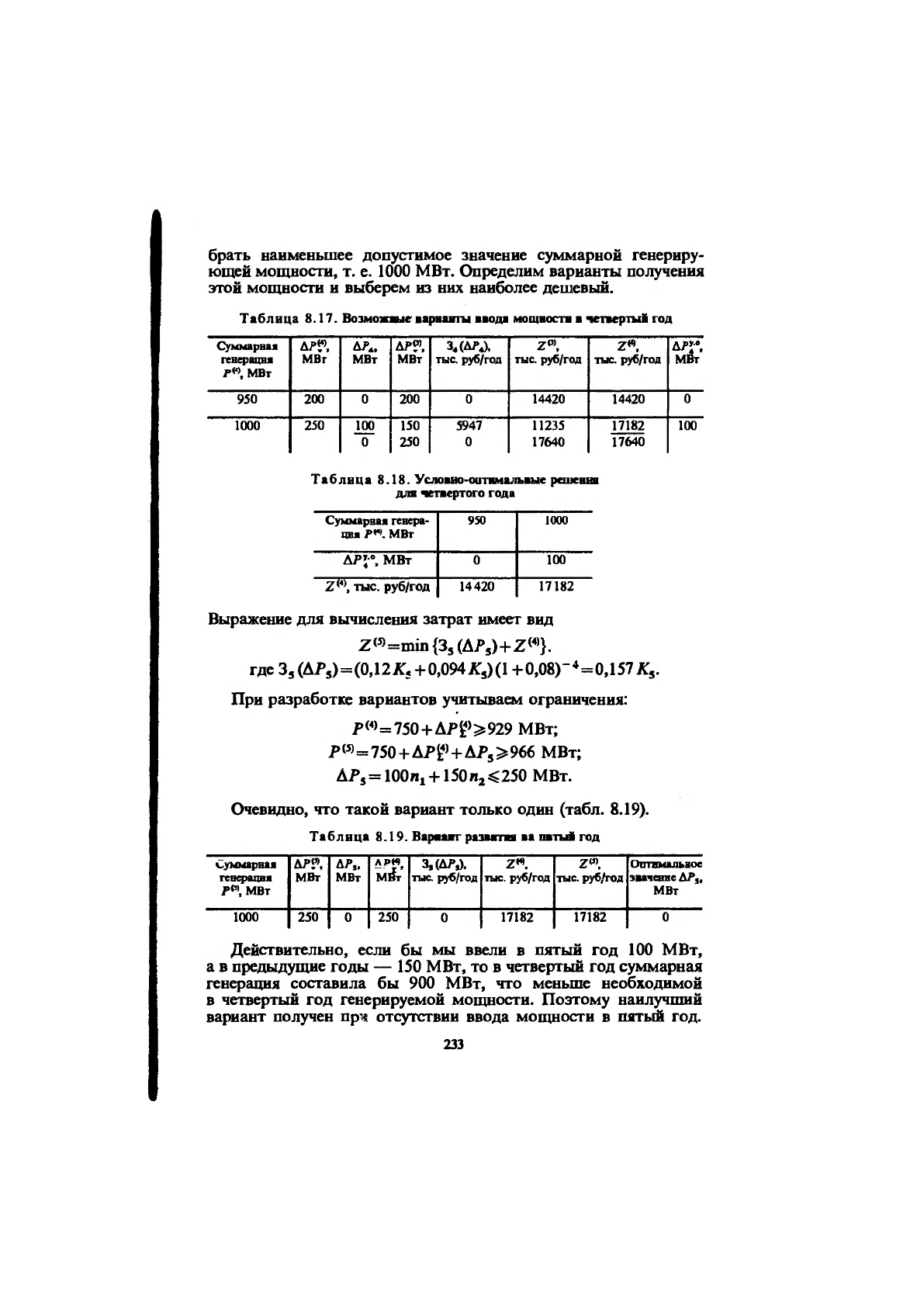
брать наименьшее допустимое значение суммарной генериру-

ющей мощности, т. е. 1000 МВт. Определим варианты получения

этой мощности и выберем из них наиболее дешевый.

Таблица 8.17. Возможаые варналы ввода мощносп в чегаершй год

Суммарная

генерацня

МВт

МВт МВт МВт

ЗЛЛРЛ

тыс. руб/год

Z<".

тыс. руб/гсщ

тыс. руб/год

МЙт

950 200 0 200 0 14420 14420 0

1000

250

100

150

250

5947

11235

17640

17182

17640

100

Таблица 8.18. Условио-оотммальвые решения

для четвертого года

Суммарная генера-

950 1000

ция МВт

API". МВт 0

100

тыс. руб/год 14420 17182

Выражение для вычисления затрат имеет вид

Z«=mm

{З5

где

З3

(АР5)=(0,12 +0,094 л:,)

+ 0,08) -=0,157 л:,.

При разработке вариантов учитываем ограничения:

pW=750+APg>>929 МВт;

Р<«=750+АР?ЧАР5>966 МВТ;

АР5

100И1

+ 150И2<250 МВТ.

Очевидно,

ЧТО

такой вариант только один (табл. 8.19).

Таблица 8.19. Варшшг развале ва пвтьй год

АП".

М№

АР

АРМ

Ч fАР \

Z»

тыс.

руб/год

Z®,

тыс.

руб.^год

^..уммарная

геяфаоая

МВт

АП".

М№

ЛГ 5,

МВт

Jj j).

тыс. руб/год

Z»

тыс.

руб/год

Z®,

тыс.

руб.^год

эвпенве А/»,,

МВт

1000 250 0 250 0 17182 17182

Действительно, если бы мы ввели в пятый год 100 МВт,

а в предыдущие годы — 150 МВт, то в четвертый год суммарная

генерация составила бы 900 МВт, что меньше необходимой

в четвертый год генерируемой мощности. Поэтому наилучший

вариант получен пр'4 отсутствии ввода мощности в шггьй год.

233

Аз

SQ Теперь, выполняя обратный

ход, можно найти оптимальное

решение на каждом шаге

динамического программиро-

вания.

В четвертый год суммарная

генерирующая мощность

1000

МВт.

можно

года:

По табл. 8.18 определяем

вводимую в четвертый год мо-

щность: АР^=

100

МВт. Теперь

определить генерирующую мощность на конец третьего

Рис. 8.2. Расположение источников

и потребителей

1000 -100 = 900 МВт.

По табл. 8.16 определяем мощность, вводимую в третий год:

АРз=0. К концу второго года генерирующая мощность осталась

неизменной. По табл. 8.14 определяем: при суммарной генерации

р(2)=9оо МВт ДР2=0, значит, к концу первого года генерация

имеет то же значение, а именно 900 МВт. По табл. 8.12 определя-

ем APi=

150

МВт.

Итак, оптимальное увеличение генерирующей мопдности для

расчетного периода достигается в том случае, когда в начале

первого года вводится один агрегат мощностью 150 МВт, а в на-

чале четвертого года — один агрегат мощностью 100 МВт.

Задача 8S. Для энергорайона, представленного на рис. 8.2,

спроектировать сеть наименьшей стоимости при следующих до-

пущениях:

— стоимость подстанции не учитывается,

— потерями в сетях можно пренебречь,

— стоимость линии пропорциональна передаваемой по ней

мощности.

В табл. 8.20 приведены мощности источников и нагрузок,

а в табл. 8.21 указаны стоимости передачи 1 МВт от каждого

Источника к каждому потребителю в условных единицах.

Таблица 8.20. Мощиости ш ш ••им н поттебигелей

Наэашаве Потребителн

А1

А2 A3 В1

В2 ВЗ

Мощность,

МВт

60 50 70 40 60 80

234

Таблнца 8.21. Стовмосп передач

еданцы мощноств

ИстОЯНИЕВ

11о11«вители

В1

В2

вз

А1 1 2 3

А2 2 1 3

2 4

Решенве. При указанных BMUJC допущениях задачу поиска

оптимальной сети правомерно рассмотреть как транспортную

[8,2. 8.S, 8.8]. Занесем условия задачи в транспортную таблицу

(табл. 8.22). В неЁ указаны мощности источников и потребителей,

а в верхнем углу кая;дой клетки указана стоимость передачи

1 МВт от источника к потребителю. Так, стоимость передачи

1 МВт от источника А1 к потребителю В1 составляет 1 усл. ед.

Таблица 8.22. Тражяорпаа таблвца

Потребители

В1 В2

ВЗ

40 60 80

Источники

А1

1 2

Источники

А2 50

1 3

Источники

АЗ

2 4

Обозначим мощность, передаваемую от источника i к потре-

бителю у, как

Хф

а стоимость передачи единшцл мощности — как

Cf/. Тогда формулировку транспортной задачи можно записать

так: найти такие значения Ху'^0, чтобы целевая функция (8.16)

достигала минимального значения при ограничениях (8.17)

и (8.18):

... + X Z

i-U-l

Yxy^bj /=1,2,..., и;

(8.16)

(8.17)

235

"Zxy^a,, i=l,2,...,m. (8.18)

Условия (8.17) и (8.18) называются балансными условиями

и соответствуют балансу мощности в узлах с источниками и по-

требителями.

Поскольку в заданных условиях сумма мощностей источни-

ков равна в точности сумме мощностей потребителей, задача

является закрытой:

т я

1-1 J-i

Наметим исходный допустимый план поставок от источников

к потребителям по вшменьшему элементу Су в строке. Такой

план показан в табл. 8.23.

Таблица 8.23. ИсходвыХ доцустнмыя плав

Потребители

40 60 80

Источники

" 40

" 20

Источники

" 40

" 10

Источники

~ 70

Величины поставок указаны в нижнем правом углу клеток.

Определим стоимость такого плана:

Z=JX 1.40 + 2.20 +1.40 + 3.10 + 4.70 =430.

J J

Приведенный план поставок является допустимым, так как выпо-

лнены балансы в узлах с источниками и потребителями. Клетки

с поставками соответствуют базисным переменным. Остальные

переменные являются свободными, и их значения равны нулю.

Число базисных переменных в допустимом плане равно /п+п

—

Применительно к рассматриваемой задаче т=3, и=3.

допусти-

мом плане табл. 8.23 содержится пять базисных клеток (для них

подчеркнуты значения коэ^ициентов с^.

С помощью метода потенциалов проверим, можно ли улуч-

шить приведенный выше план поставок [8.5, 8.8]. Назначим поте-

нциал первой строки равным нулю (ui =

и определим потенци-

алы остальных строк и столбцов; для этого используем то обсто-

ятельство, что для базисньа клеток должно выполняться соот-

ношение U/-b Число таких уравнений {т+п— 1):

236

+ V2 =

C22

U2 +

= C23 = 3;

«3

+ V3'=C33=4;

Остальные потенциалы имеют такие значения:

= l, V2=2, U2=-1, V4=4, МЗ=0.

Определим, можно ли улучшить это решение. Если для сво-

бодных клеток

Су=Су—Ui

О,

то возможно снижение значения

целевой функции:

с.з = 3-0-4=-1;

с,1

= 2-1 +

21 •

Сз2

= 2-0-2=0.

'31

= 1-0-1 = 0;

Итак, решение, приведенное в табл. 8.23, можно улучшить,

если ввести в число базисных переменную .хг^з- Цикл пересчета

включает эту переменную и базисные переменные J^az и

Величина поставки определяется как наименьшее значение из

поставок в отрицательных вершинах. Отрицательными вершина-

ми являются клетки 1—2 и 2—3. Таким образом, переменная х^з

в новом плане имеет значение

х^з

10.

В табл. 8.24 приведен

новый улучшенный план поставок. Там же показаны новые значе-

ния потенциалов. При их вычислении было принято, что = 0.

Таблица 8.24. Улучшенный плав поставок

Потребш-еяв Потсацвалы

60 80

Источники

~ 40

~ 10

Источники

~ 50

-1

Источники

~ 70 1

Потен-

циалы

"У

2 3

Значение целевой функции для данного решения

Z = 1.40-и 2.10

4-3.10-f-1.50

+ 4.70 =420.

Проанализируем, возможно ли улучшить решение, приведен-

ное в табл. 8.24. Дня этого вычислим для свободных клеток

хараггеристики:

237

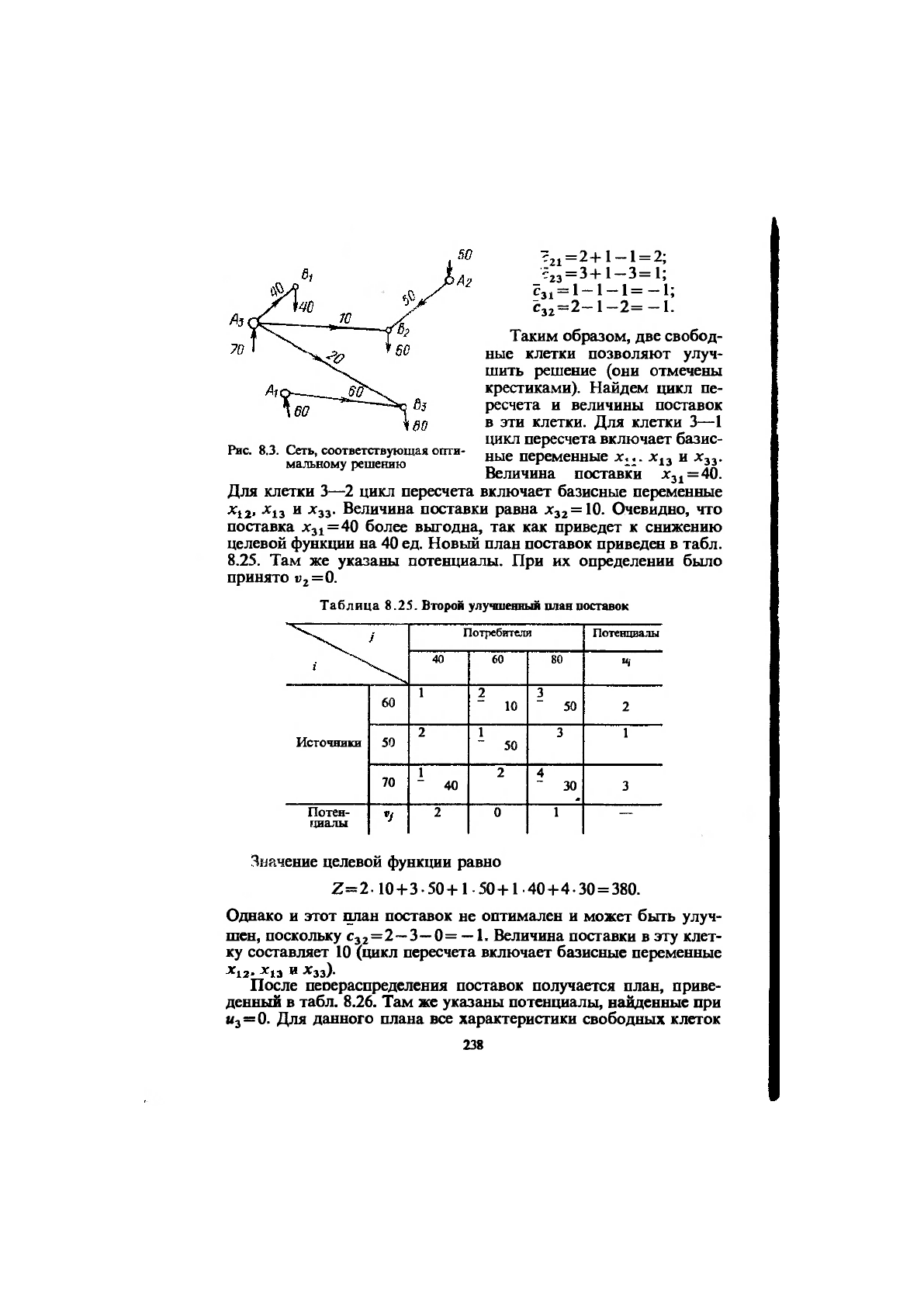
:21

-23

=2+1-1 = 2;

= 3+1-3=1;

Сз, = 1-1-1 = -1;

Сз2=2-1-2=-1.

Таким образом, две свобод-

ные клетки позволяют улуч-

шить решение (они отмечены

крестиками). Найдем цикл пе-

ресчета и величины поставок

в эти клетки. Для клетки 3—1

Ш1КЛ

пересчета включает базис-

ные переменные дг^з и Х33.

Величина поставки Хз^=40.

Для клетки 3—2 цикл пересчета включает базисные переменные

-«13 и Х33. Величина поставки равна Хз2=10. Очевидно, что

поставка Хз1=40 более выгодна, так как приведет к снижению

целевой функции на 40 ед. Новый план поставок приведен в табл.

8.25. Там же указаны потенциалы. При их определении было

принято «2=0.

Таблица 8.25. Второй улучшенный план поставок

Рис. 8.3. Сеть, соответствующая опти-

мальному решению

Потребители

Потенциалы

60 SO

Источники

1 2

~ 10

" 50

Источники

" 50

Источники

~ 40

2 4

- 30 3

Потен-

циалы

2 0

Змачение целевой функции равно

Z=2.10 + 3-50+1 50+1-40 +4.30 = 380.

Однако и этот шин поставок не оптимален и может быть улуч-

шен, поскольку СЗ2=2~3—0=

—

I. Величина поставки в эту клет-

ку составляет 10 (цикл пересчета включает базисные переменные

*зз)-

После пгаераспределения поставок получается план, приве-

денный в табл. 8.26. Там же указаны потенциалы, Ба]^енные при

из=0. Для данного плана все характеристики свободных клеток

238

положительны: Cy—Cij—ut—vp Это означает, что данный план

оптимален. Целевая функция имеет значение

Z=3.60+l.50+1.40 +2-10 + 4.20 = 370.

Таблица 8.26. 01]тямальяы% план оостшсж

Потребители

Потенциалы

40 60 80

Источники

" 60

-1

Источники 50

2 1

~ 50

3 -1

Источники

~ 40

~ 10

" 20

Потен-

циалы

«1

1 2

На рис. 8.3 показана сеть, соответствующая данному реше-

нию. Отметим, что постановка задачи не предусматривала воз-

можности транзита мощности через шины источников и потреби-

телей.