Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

220 3 Oceans and Atmospheres

where

∇

∂

∂φ

∂

∂ν

ν =ln



1 +tan

1 −tan



and φ and λ are longitude and latitude angles.

Show that if solutions are sought in a narrow canal at latitude λ with ends

at φ =±

, and boundary conditions of no ﬂow through the boundaries, i.e.,

∂

∂n

(η −χ) = 0,

then

η =

cos

δ cos

1 −S

cos

[A cos 2St +B sin 2St],

where

A =cos2φ −

S cos λ sin L cos(2Sφ cos λ)

sin(LS cos λ)

B =−sin2φ +

S cos λ cos L sin(2Sφ cos λ)

cos(LS cos λ)

3.12 A tsunami is modelled by the wave equation

∂

∂t

∂

∂r



∂η

∂r



subject to the conditions that

η =0att =0,r=0,

η →0asr →∞,

2π



∞

rηdr ≡V.

Show that a similarity solution of this problem can be found in which

η =

f(ξ), ξ =

and that f satisﬁes the equation







=(ξf



)



;

3.13 Exercises 221

write down the boundary condition and integral constraint for f .

Show that there exists a solution of the form

f =

(1 −ξ

)

3/2



(1 −s

)

1/2

, 0 <s<1,

f =

(ξ

−1)

3/2



−1)

1/2

,s>1,

if we assume f is ﬁnite at ξ =1.

Show that this solution is continuous at ξ =1 but has discontinuous deriva-

tive there. Show also that the solution in ξ>1 cannot satisfy the integral

constraint on f .

Suppose instead that the solution above in ξ<1 is correct, but f = 0in

ξ>1. Use the integral constraint to show that

A =

2π[1 −ln 2]

and show that the wave front at r =t is of height

Does this solution make sense? Is the position of the wave front uniquely

deﬁned? Show that f ∼−A ln ξ as ξ → 0, and deduce (explaining why) that

no solution of this type is appropriate.

3.13 The stream function ψ of the ocean circulation satisﬁes the equation

βψ

=−1 +E

∇

in the closed domain B, with boundary conditions

ψ =

∂ψ

∂n

=0on∂B.

If B is the box 0 <x<1, 0 <y<1, ﬁnd a suitable scaling for the bound-

ary layer near y = 0, and hence show that in terms of the rescaled boundary

layer coordinates x and Y , ψ satisﬁes the boundary layer equation

βψ

=−1 +ψ

YYYY

together with the boundary conditions

ψ =ψ

=0onY =0,ψ→∞ as Y →∞,

and the ‘initial’ condition

ψ =0onx =1.

Show that a similarity solution for this equation exists in the form

ψ =



1 −x





1 −f(η)



,η=Y



1 −x



1/4

222 3 Oceans and Atmospheres

and that f satisﬁes the equation

−ηf



+4f =0,

with

f(0) =1,f



(0) =0,f(∞) =0.

Find four independent possible asymptotic behaviours for f as η →∞,

and show that only two tend to zero. Hence deduce that the given boundary

conditions should be sufﬁcient to determine the solution uniquely.

3.14 The normalised amplitude of a tsunami wave satisﬁes the equation

=φ

Seek solutions valid for large r and t by changing variables to ξ = r −t and

τ = t, and show that an asymptotic solution for large t can be found with the

assumption that

φ ∼

∞



(ξ)

Show that φ



, φ



=−

ξφ

−

, and hence ﬁnd the expansion

for φ correct to terms of O(

), assuming that φ

is known.

Chapter 4

River Flow

Much of the environment consists of ﬂuids, and much of this book is therefore

concerned with ﬂuid mechanics. Oceans and atmosphere consist of ﬂuids in large

scale motion, and even later, when we deal with more esoteric subjects: the ﬂow of

glaciers, convection in the Earth’s mantle, it is within the context of ﬂuid mechanics

that we formulate relevant models. This chapter concerns one of the most obvious

common examples of a ﬂuid in motion, that of the mechanics of rivers.

Fluid mechanics in the environment is, however, altogether different to the sub-

ject we study in an undergraduate course on viscous ﬂow, and the principal reason

for this is that for most of the common environmental ﬂuid ﬂows with which we

are familiar, the ﬂow is turbulent. (Where it is not, for example in glacier ﬂow,

other physical complications obtrude.) As a consequence, the models which we use

to describe the ﬂow are different to (and in fact, simpler than) the Navier–Stokes

equations.

4.1 The Hydrological Cycle

Rainwater which falls in a catchment area of a particular river basin makes its way

back to the ocean (or sometimes to an inland lake) by seepage into the ground,

and then through groundwater ﬂow to outlet streams and rivers. In severe storm

conditions, or where the soil is relatively impermeable, the rainfall intensity may

exceed the soil inﬁltration capacity, and then direct runoff to discharge streams can

occur as overland ﬂow. Depending on local topography, soil cover, vegetation, one

or other transport process may be the norm. Overland ﬂow can also occur if the soil

becomes saturated. The hydrological cycle is completed when the water, now back

in the ocean, is evaporated by solar radiation, forming atmospheric clouds which are

the instrument of precipitation.

River ﬂow itself occurs on river beds that are typically quasi-one-dimensional,

sinuous channels with variable and rough cross section. Moreover, if the channel

A. Fowler, Mathematical Geoscience, Interdisciplinary Applied Mathematics 36,

DOI 10.1007/978-0-85729-721-1_4, © Springer-Verlag London Limited 2011

223

224 4 River Flow

discharge is Q (m

−1

), and the wetted perimeter length of the cross section is l

(m), then an appropriate Reynolds number for the ﬂow is

Re =

νl

, (4.1)

where ν =μ/ρ is the kinematic viscosity (and μ is the dynamic viscosity). If l =

20 m, ν =10

−6

−1

, Q =10 m

−1

, then Re ∼0.5 ×10

. Inevitably, river ﬂow

is turbulent for all but the smallest rivulets. A different measure of the Reynolds

number is

Re =

, (4.2)

where u is mean velocity and h is mean depth. In a wide channel, we ﬁnd that the

width is approximately l, so that Q ≈ ulh, and this gives the same deﬁnition as

(4.1). Thus, to model river ﬂow, and to explain the response of river discharge to

storm conditions, as measured on ﬂood hydrographs, for instance, one must model

a ﬂow which is essentially turbulent, and which exists in a rough, irregular channel.

The classical way in which this is done is by applying a time average to the

Navier–Stokes equations, which leads to Reynolds’ equation, which is essentially

like the Navier–Stokes equation, but with the stress tensor being augmented by a

Reynolds stress tensor. The procedure is described in Appendix B.

For a ﬂow u =(u,v,w) which is locally unidirectional on average, such as that

in a river, we may take the mean velocity

u =( ¯u, 0, 0), and then the x component

of the momentum equation becomes

∂

∂z

(



) ≈−

∂ ¯p

∂x

+μ

∂

¯u

∂z

, (4.3)

because in a shallow ﬂow, the other Reynolds stress terms are smaller. Integration

over the depth shows that the resistance to motion is provided by the wall stress τ ,

and this is

τ =μ

∂ ¯u

∂z

+{−ρ



}, (4.4)

evaluated at the wetted perimeter of the ﬂow. Strictly, the Reynolds stress vanishes

at the boundary (because the ﬂuid velocity is zero there), and the molecular stress

changes rapidly to compensate, in a very thin laminar wall layer. Normally one

evaluates (4.4) just outside this layer, close to but not at the boundary, where the

molecular stress is negligible and the Reynolds stress is parameterised in some way.

A common choice is to use a friction factor, thus

τ =fρ ¯u

, (4.5)

where the dimensionless number f (called the friction factor) is found to depend

rather weakly on the Reynolds number.

A crude but effective assumption is simply

that f is constant, with a typical value for f of 0.01.

More precisely, the stress should be τ = fρ|¯u|¯u, since the friction acts in the opposite direction

to the ﬂow. For unidirectional ﬂows, this reduces to (4.5). Later (in Sect. 4.5.3), we will have need

for this more precise formula.

4.2 Chézy’s and Manning’s Laws 225

4.2 Chézy’s and Manning’s Laws

Our starting point is that the ﬂow is essentially one-dimensional: or at least, we focus

on this aspect of it. As well as the cross-sectional area (of the ﬂow) A and discharge

Q, we introduce a longitudinal, curvilinear distance coordinate s, and we assume

that the river axis changes direction slowly with s. Then conservation of mass is, in

its simplest form,

∂A

∂t

∂Q

∂s

=M. (4.6)

This source term M represents the supply to the river due to inﬁltration seepage and

overland ﬂow from the catchment.

(4.6) must be supplemented by an equation for Q as a function of A, and this

arises through consideration of momentum conservation. There are three levels at

which one may do this: by exact speciﬁcation, as in the Navier–Stokes momentum

equation; by ignoring inertia and averaging, as in Darcy’s law; and most simply, by

ignoring inertia and applying a force balance using a semi-empirical friction factor.

We begin by opting for this last choice, which should apply for sufﬁciently ‘slow’

(in some sense) ﬂow. Later we will consider more complicated models.

We have already deﬁned the Reynolds number Re in terms of Q and A, or equiv-

alently a mean velocity u =Q/A and a channel depth d ∼A

1/2

. ‘Slow’ here means

asmallFroude number, deﬁned by

Fr =

(gd)

1/2

5/4

. (4.7)

If Fr < 1, the ﬂow is tranquil;ifFr > 1, it is rapid. Gravity is of relevance, since

the ﬂow is ultimately due to gravity.

Now let l be the wetted perimeter of a cross section, and let τ be the mean shear

stress exerted at the bed (longitudinally) by the ﬂow. If the downstream angle of

slope is α, then a force balance gives

lτ =ρgAsin α, (4.8)

where ρ is density. For turbulent ﬂow, the shear stress is given by the friction law

τ =fρu

, (4.9)

where the friction factor f may depend on the Reynolds number. Since

u =Q/A, (4.10)

and deﬁning the hydraulic radius

R =A/l, (4.11)

we derive the relations

u =(g/f )

1/2

, (4.12)

where

S =sin α, (4.13)

226 4 River Flow

and

Q =





1/2

3/2

1/2

. (4.14)

For wide, shallow rivers, l is essentially the width. For a more circular cross section,

l ∼A

1/2

, and

Q =(g/f )

1/2

5/4

1/2

. (4.15)

Therelation(4.12) is the Chézy velocity formula, and C = (g/f )

1/2

is the Chézy

roughness coefﬁcient. Notice that the Froude number, in terms of the hydraulic ra-

dius, is

Fr =

(gR)

1/2

=(S/f )

1/2

, (4.16)

and tranquillity (at least in uniform ﬂow) is basically due to slope.

Alternative friction correlations exist. That due to Manning is an empirical for-

mula to ﬁt measured stream velocities, and is of the form

u =R

2/3

1/2



, (4.17)

where Manning’s roughness coefﬁcient n



takes typical values in the range 0.01–

0.1 m

−1/3

s, depending on stream depth, roughness, etc. Manning’s law can be de-

rived from an expression for the shear stress of the form (cf. (4.9))

τ =

ρgn

2

1/3

. (4.18)

For Manning’s formula, we have

Q ∼A

4/3

if R ∼A

1/2

Q ∼A

5/3

if l is width,R=A/l ∼A.

(4.19)

Thus we see that for a variety of stream types and velocity laws, we can pose a

relation between discharge and area of the form

Q ∼A

m+1

,m>0, (4.20)

with typical values m =

–

. In practice, for a given stream, one could attempt to

ﬁt a law of the form (4.20) by direct measurement.

4.3 The Flood Hydrograph

Suppose in general that

Q =

m+1

m +1

. (4.21)

We can non-dimensionalise the equation for A so that it becomes

∂A

∂t

∂A

∂s

=M, (4.22)

4.3 The Flood Hydrograph 227

Fig. 4.1 Formation of a

shockwaveinthesolutionof

(4.22)(cf.Fig.1.14)

a ﬁrst-order nonlinear hyperbolic equation, also known as a kinematic wave equa-

tion, whose solution can be written down. The source term M is in general a function

of s and t , but for simplicity we take it to be constant here. Suppose the initial data

are parameterised as

A = A

(σ ), s =σ>0,t=0. (4.23)

Then the characteristic equations are

=M,

, (4.24)

whence

A =A

(σ ) +Mt, s = σ +

+Mt)

m+1

−A

m+1

M(m +1)

, (4.25)

thus

A = Mt +A



s −



m+1

−(A −Mt)

m+1

M(m +1)



(4.26)

determines A implicitly.

We can see from (4.26) that this solution applies for sufﬁciently small t or large

s, since we must have σ>0. For larger t, the characteristics are those emanating

from s =0, where the boundary data are parameterised by

A =0,s=0,t=τ, (4.27)

and the solution is the steady state

m+1

m +1

=Ms. (4.28)

This steady state is applicable above the dividing characteristic in the (s, t) plane

emanating from the origin, which is

s =

m+1

m +1

. (4.29)

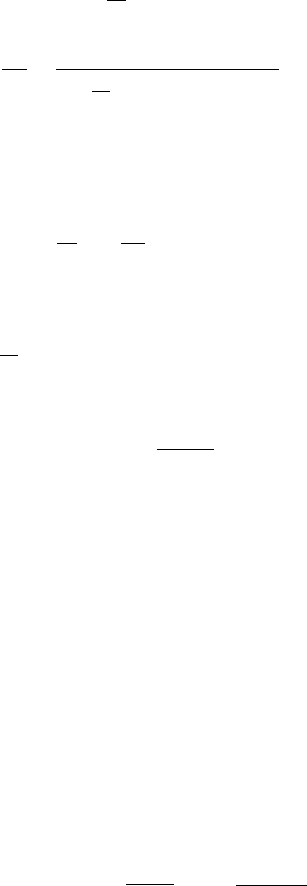
228 4 River Flow

Thus any initial disturbance to the steady state is washed out of the system in a ﬁnite

time (for any ﬁnite s).

From (4.26) we can calculate

∂A

∂s

explicitly in terms of t and the characteristic

parameter σ , and the result is

∂A

∂s



1 +



{(A

+Mt)

−A

}

. (4.30)

It is a familiar fact that humped initial conditions A

(σ ) will lead to propagation of

a kinematic wave, and then to shock formation, as shown in Fig. 4.1, when ∂A/∂s

reaches inﬁnity. From (4.30), we see that this occurs on the characteristic through

s =σ for t>0ifA



< 0, when

t =t



−





1/m

−A



, (4.31)

and a shock forms when t =min

> 0. Thereafter a shock exists at a point s

(t),

and propagates at a rate given, by consideration of the integral conservation law

∂

∂t



Ads =−[Q]



Mds, (4.32)

˙s

[Q]

−

[A]

−

. (4.33)

As an application, we consider the ﬂood hydrograph, which measures discharge

at a ﬁxed value of s as a function of time. Suppose for simplicity that M = 0(the

case M>0 is considered in Question 4.7). As an idealisation of a ﬂood, we consider

the initial condition

A ≈A

∗

δ(s) at t =0, (4.34)

where δ(s) is the delta function, representing the input to the river by overland ﬂow

after a short period of localised rainfall. Either directly, or by letting M → 0in

(4.26), we have A = A

(s −A

t), and it follows that A ≈0 except where s =A

The humped initial condition causes a shock to form at s

(t), with s

(0) = 0, and

we have

A =0,s>s

A =(s/t)

1/m

,s<s

(4.35)

asshowninFig.4.2.

The shock speed is given by

˙s

=(Q/A)|

−

m +1



−

(m +1)t

, (4.36)

whence s

∝ t

1/(m+1)

. To calculate the coefﬁcient of proportionality, we use con-

servation of mass in the form



Ads =A

∗

, (4.37)

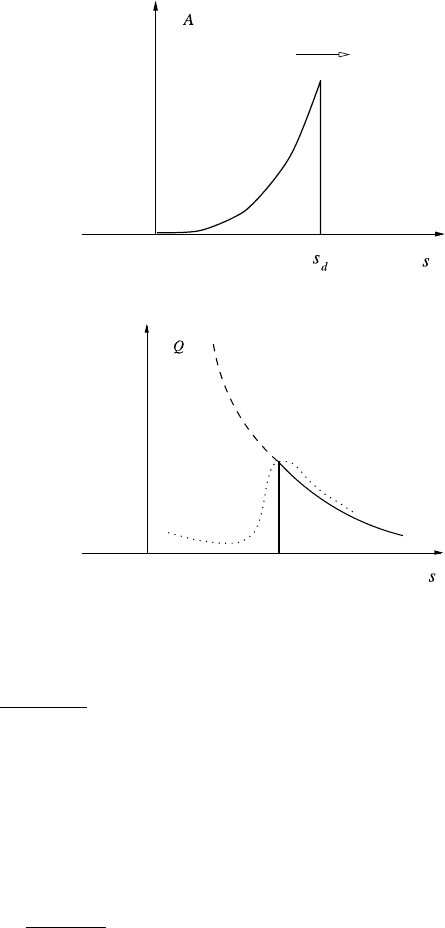
4.3 The Flood Hydrograph 229

Fig. 4.2 Propagation of a

shock front

Fig. 4.3 Ideal (full line)and

observed (dotted line)

hydrographs

whence, in fact,



(m +1)A

∗



m/(m+1)

1/(m+1)

. (4.38)

Denoting b =[(m +1)A

∗

/m]

m/(m+1)

, the ﬂood hydrograph at a ﬁxed station s = s

∗

is then as follows. For t<t

∗

, where

∗

=(s

∗

/b)

m+1

, (4.39)

Q =0. For t>t

∗

, A =(s

∗

/t)

1/m

, and thus

Q =

∗(m+1)/m

(m +1)

−(m+1)/m

. (4.40)

This result is illustrated in Fig. 4.3, together with a typical observed hydrograph.

The smoothed observation can be explained by the fact that a more realistic initial

condition would have delivery of the storm ﬂow over an interval of space and time.

More importantly, one can expect that a more realistic model will allow for diffusive

effects.