Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

230 4 River Flow

4.4 St. Venant Equations

We now re-examine the momentum equation, which we previously assumed to be

described by a force balance. Again consider the equations in dimensional form. For

the remainder of the chapter we take M =0, largely for simplicity. Conservation of

mass can then be written in the form

∂A

∂t

∂

∂s

(Au) = 0, (4.41)

where the mean velocity u is deﬁned by

u =

, (4.42)

and then conservation of momentum (from ﬁrst principles) leads to the equation

(adopting the friction law (4.9))

∂(Au)

∂t

+ρ

∂

∂s





=ρgAS −ρlf u

−

∂

∂s

(A ¯p), (4.43)

where ¯p is the mean pressure. Now the pressure is approximately hydrostatic, thus

p ≈ ρgz where z is depth. Then ¯pA ≈



ρgh

dx where h is total depth and x is

width, and thus

∂

∂s

(A ¯p) =ρg



∂h

∂s

dA; (4.44)

if we suppose ∂h/∂s is independent of x, we ﬁnd

∂

∂s

(A ¯p) =ρgA

∂

∂s

, (4.45)

where

h is the mean depth. Using (4.41), (4.43) reduces to

+uu

=gS −

flu

−g

∂

∂s

. (4.46)

Equations (4.41) and (4.46) are known as the St. Venant equations.

The assumption that ∂h/∂s is constant across the stream means that along a transverse section

of the river, the surface is horizontal. This is really due to the smallness of the width compared

to the length. It is importantly not exactly true for meandering rivers, but is still a very good

approximation.

Note that the derivation of (4.46) assumes a constant slope S. If the slope is varying, then the

derivation is still valid providing S is the local bed slope. If we then take

S to be the average

downstream slope, and denote the bed by z =b(s) and the surface by z = η(s), we have the local

slope S =

S − b

, and thus S −h

S − η

, and thus (4.46) still applies for varying bed slope

when S denotes the (constant) mean slope, providing we replace

h by η. All of this supposes that

b does not vary with x, i.e., the channel section is rectangular.

4.4 St. Venant Equations 231

4.4.1 Non-dimensionalisation

We choose scales for u =Q/A, t, s, A, R (the hydraulic radius, = A/l) and

h as

follows, in keeping with the assumed balances adopted earlier:

Au ∼Q, gS ∼

lf u

t ∼

,s∼

h, R ∼d,

(4.47)

where we can suppose Q is a typical observed discharge, and d is a typical observed

depth. Explicitly, the scales are

[

h], [R]=d, [s]=

[u]=



gdS



1/2

, [t]=





1/2

, [A]=Q



gdS



1/2

(4.48)

and we put u =[u]u

∗

, etc., and drop asterisks. The resulting equations are

+(Au)

=0,

+uu

]=1 −

−h

(4.49)

where we would choose h ∼R ∼A for a wide channel, h ∼R ∼A

1/2

for a rounded

channel. In particular, for a wide channel, we have R = h, so that the momentum

equation can be written

(wh)

+(wuh)

=0,

+uu

) =1 −

−h

(4.50)

since A =wh, where w is the (dimensionless) width. As before, the Froude number

F is given by

F =

[u]

(gd)

1/2





1/2

. (4.51)

4.4.2 Long Wave and Short Wave Approximation

To estimate some of these scales, we take d = 2m,u = 1ms

−1

and S = sinα =

0.001, typical lowland valley values. We then have the length scale [s]=

∼2km,

and the time scale t ∼ 33 minutes, and in some sense these are the natural length

and time scales for the dynamic river response. However, it is fairly clear that these

scales are not appropriate either for variations over the length of a whole river, or for

the shorter length and time scales appropriate to waves generated by passage of a

boat, for example. Both of these situations lead to further simpliﬁcations, as detailed

below.

232 4 River Flow

Long Wave Theory

Suppose we have a river of length L = 100 km, and we are concerned with the

passage of a ﬂood wave along its length. It is then appropriate to rescale s and t as

s ∼

,t∼

,ε=

,H=L sin α; (4.52)

note that H is the drop in elevation of the river over its length L: in this instance

ε ∼0.02 1. In this case equations (4.50) become

+(uh)

=0,

εF

+uu

) =1 −

−εh

(4.53)

and in the limit ε →0, we regain the slowly varying ﬂow approximation.

Short Wave Theory

An alternative approximation is appropriate if length scales are much shorter than

2 km. This is often the case, and particularly in dynamically generated waves, as we

discuss further below. In this case, it is appropriate to rescale length and time as

s ∼δ, t ∼δ, δ =

, (4.54)

where now δ 1, and then the model equations (4.50) become

+(uh)

=0,

+uu

) =δ



1 −



−h

(4.55)

and when δ is put to zero, we regain the shallow water equations of ﬂuid dynamics.

4.4.3 The Monoclinal Flood Wave

One of the suggestions made at the end of Sect. 4.3 was that the shocks predicted by

the slowly varying ﬂood wave theory would in reality be smoothed out by some

higher-order physical effect. This shock structure is called the monoclinal ﬂood

wave (because it is a monotonic proﬁle), and it can be understood in the context

of the long wave St. Venant theory (4.53). The simplest version is when F 1as

well as ε 1, for then we can approximate the momentum equation (4.53)

by the

relation

u ≈h

1/2



1 −

εh

...



, (4.56)

4.4 St. Venant Equations 233

and (4.53)

becomes

∂h

∂t

1/2

≈

∂

∂s



3/2

∂h

∂s



. (4.57)

This is a convective diffusion equation much like Burgers’ equation, and we ex-

pect it to support a monoclinal wave which provides a shock structure joining values

−

upstream to lower values h

downstream. We analyse this shock structure by

writing

s =s

+εX, (4.58)

where s

is the ﬂood wavefront, and X is a local coordinate within the shock struc-

ture. To leading order we then obtain the equation

−ch



3/2



1 −



=0, (4.59)

where c =˙s

is the wave speed. Integrating this, we obtain

ch =h

3/2



1 −



+K, (4.60)

where we require

K =ch

−

−h

3/2

−

=ch

−h

3/2

(4.61)

(which gives the shock speed determined in the usual way by the jump condition

c =[h

3/2

]

−

/[h]

−

). Hence h is given by the quadrature

2X =



3/2

[ch −h

3/2

]−K

, (4.62)

where the arbitrary choice of h

∈(h

−

) simply ﬁxes the origin of X.(4.62) can

be simpliﬁed to give

X =



(w −w

)(w

−

−w)(w +C)

, (4.63)

where w =h

1/2

, and

C =

−

, (4.64)

and X(w) can of course be evaluated.

Of particular interest is the small ﬂood limit, in which w =w

−

−w

is small.

In this case C ≈

, and h can be found explicitly, as the approximation

h =



1/2

−

−X/X

1 +e

−X/X



, (4.65)

where

X =

3w

3h

(4.66)

234 4 River Flow

Fig. 4.4 The monoclinal

ﬂood wave given by (4.65),

with h

−

=1.5, h

=1,

X =1

is the shock width. A further simpliﬁcation (because h =h

−

−h

is small) is

h =h

h e

−X/X

1 +e

−X/X

. (4.67)

In dimensional terms, the shock width is of order

d sinα

, (4.68)

where d is the depth, and d is the change in depth. Following a storm, if a river of

depth two metres and bedslope 10

−3

rises by a foot (thirty centimetres), the shock

width is about thirteen kilometres: not very shock-like! Figure 4.4 shows the form

of the monoclinal ﬂood wave (as given by (4.65)).

Although (4.57) is useful in indicating the diffusive structure of the long wave

theory, the above discussion of the monoclinal ﬂood wave is strictly inaccurate,

since the approximation in (4.56) breaks down on short scales. To see that the anal-

ysis still holds, we can re-do the analysis on the full system (4.53). Adopting (4.58),

we ﬁnd, approximately,

−ch

+(uh)

=0,

(−cu

+uu

) =1 −

−h

(4.69)

with ﬁrst integral

ch =K +uh, (4.70)

with K and c determined by (4.61) as before, noting that u

√

, and thus

,asusedin(4.63).

We then ﬁnd that

−(ch −K)

−K

, (4.71)

4.4 St. Venant Equations 235

and (4.63) is replaced by

X =



−K

)dh

(h −h

)(h

−

−h)(h −A)

, (4.72)

where

A =

−



−



. (4.73)

Clearly A<h

−

, and thus the ﬂood wave connecting h

−

to h

as X increases

exists (with h

−

) if the numerator in (4.72) is positive for all h>h

, which is

the case, using the deﬁnition of

K =

−

√

−

, (4.74)

−



−

. (4.75)

Since h

−

, the upper limit of the right hand side is two, so that the monoclinal

ﬂood wave cannot exist for F>2, consistent with the fact that roll waves then form,

as we now show.

4.4.4 Waves and Instability

The monoclinal ﬂood wave is one example of a river wave. More generally, we

can expect disturbances to a uniformly ﬂowing stream to cause waves to propagate,

and in this section we study such waves. In particular, we will ﬁnd that if the basic

ﬂow is sufﬁciently rapid, then disturbance waves will grow unstably. Such waves

are commonly seen in fast ﬂowing rivulets, for example on steep pavements during

rainfall, and even on car windscreens.

To analyse waves on rivers, we take the basic river ﬂow as being (locally) con-

stant, thus in (4.50) (with R =h)

u =h = 1, (4.76)

and we examine its stability by writing

u =1 +v, h =1 +H, (4.77)

and linearising. We obtain the linear system

=0,

) =−2v +H −H

(4.78)

whence



∂

∂t

∂

∂s



v =−2



∂

∂t

∂

∂s



v −v

. (4.79)

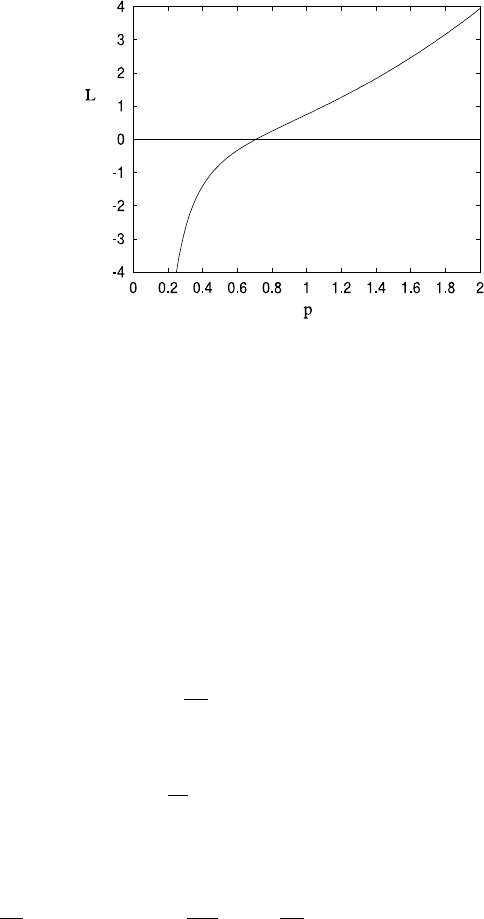
236 4 River Flow

Fig. 4.5 The function L(p)

deﬁned by (4.85), with

k =1

Solutions v = exp[iks +σt] exist, provided σ satisﬁes

(σ +ik)

+2(σ +ik) +ik +k

=0, (4.80)

˜σ =−i

k −1 ±



1 −i

k −



1/2

, (4.81)

where we write

σ =˜σ/F

,k=

k/F

. (4.82)

There are thus two wave-like disturbances. The possibility of instability exists, if

either value of ˜σ has positive real part. We deﬁne the positive square root in (4.81)

to be that with positive real part. Speciﬁcally, we deﬁne

p +ikq =



1 −i

k −



1/2

, (4.83)

where we take p>0; thus, the real and imaginary parts of ˜σ are given by

˜σ

=±p −1, −

˜σ

=1 ∓q, (4.84)

and the criterion for instability is that ˜σ

> 0, i.e., p>1. In this form, the growth

rate of the wave is ˜σ

, while the wave speed is −˜σ

k.From(4.83), we ﬁnd

q =−

,L(p)≡p

−

=1 −

. (4.85)

As illustrated in Fig. 4.5, L(p) is a monotonically increasing function of p, and

therefore the instability criterion p>1 is equivalent to L(p) > L(1). Since p is

determined by L(p) =1 −(

), while from (4.85), L(1) =1 −(

/4),wesee

that instability occurs if

F>F

=2. (4.86)

4.5 Nonlinear Waves 237

Thus, for tranquil ﬂow, F<O(1), the ﬂow is stable. For rapid ﬂow, F>O(1),

it can be unstable. The wave which goes unstable (when p =1) propagates down-

stream, because its wave speed is 1 − q =

, and in fact the p>0 wave always

propagates downstream. The other wave, always stable, propagates downstream un-

less 1 +q<0, i.e., if and only if p<1/2, or equivalently,

F<F

−

(3 +4

)

1/2

. (4.87)

Note that F

−

depends on

k, and that 0 <F

−

< 1. Rewriting this inequality in terms

of F and k,itis



1 −F



, (4.88)

and upstream propagating waves are possible for short waves with k>

√

We therefore have three distinct ranges for F :

F>2: two waves downstream, one unstable;

1 <F <2: two waves downstream, both stable;

F<1: stable waves can propagate upstream and downstream.

To go further than this requires a study of the nonlinear system (4.49). We see that

the transition at F =1 is associated with the ability of waves to propagate upstream.

The transition at F =2 is sometimes called a Vedernikov instability and is associ-

ated with the formation of downstream propagating roll waves.

4.5 Nonlinear Waves

When F>2, linear disturbances will grow, and nonlinear effects become important

in limiting their eventual amplitude. Because of the hyperbolic form of the equa-

tions, we might then expect shocks to form. To examine this hyperbolic form, we

put

γ =

. (4.89)

The equations are then

+(hu)

=0,

+uu

+γ

=γ



1 −



(4.90)

and they can be written in the form

∂

∂t









∂

∂s







[1 −

]



. (4.91)

238 4 River Flow

4.5.1 Characteristics

The analysis of characteristics for systems of hyperbolic equations is described in

Chap. 1. The eigenvalues of B =





are given by

λ =u ±γh

1/2

, (4.92)

and the matrix P of eigenvectors and its inverse P

−1

are given by

P =



√

γ −γ



−1

2γ

√



√

γ −

√



. (4.93)

Comparing this with (1.69), we see that the integral



−1

du =





√

2γ

√

−

2γ





√

h +

2γ

√

h −

2γ



(4.94)

is well-deﬁned, and determines the characteristic variables (the Riemann invariants,

so called because they are constant on the characteristics in the absence of the forc-

ing gravity and friction terms, as in shallow water theory). The equations can thus

be compactly written in the characteristic form



∂

∂t



u ±γ

√



∂

∂s





u ±2γ

√



=γ



1 −



. (4.95)

Nonlinear waves propagate downstream if u/γ h

1/2

> 1, but one will propagate up-

stream if u/γ h

1/2

< 1. This is consistent with the preceding linear theory (since

u/γ h

1/2

is the local Froude number, i.e., the Froude number based on the local val-

ues of velocity and depth). Because Eqs. (4.95) are of second order, simple shock

wave formation analysis is not generally possible. Equations (4.95) are very similar

to those of gas dynamics, or the shallow water equations, and the equations support

the existence of propagating shocks in a similar way.

4.5.2 Roll Waves

There is a good deal of evidence that solutions of (4.90) do indeed form shocks,

and when these are formed via the instability when F>2, the resultant waves are

called roll waves. They are seen in steep ﬂows with relatively smooth beds (and

thus low friction), but this combination is difﬁcult to ﬁnd in natural rivers. It is

found, however, in artiﬁcial spillways, such as that shown in Fig. 4.6, which shows

a photograph of roll waves propagating down a spillway in Canada. Roll waves

can be found forming on any steep incline. Film ﬂow down steep slopes during

heavy rainfall will inevitably form a sequence of periodic waves, and these are also

roll waves; see Fig. 4.7. I used to see them frequently at my daughter’s school, for

example.

4.5 Nonlinear Waves 239

Fig. 4.6 Roll waves propagating down a spillway at Lion’s Bay, British Columbia. The width of

the ﬂow is about 2 m, and the water depth is about 10 cm. Photograph courtesy Neil Balmforth

To describe roll waves, we seek travelling wave solutions to (4.90), in the form

h = h(ξ), u = u(ξ ), where ξ = s − ct is the travelling wave coordinate, c being

the wave speed. Substitution of these into (4.90) yields the two ordinary differential

equations

−ch



+(uh)



=0,

−cu



+uu



=1 −

−γ



(4.96)

The ﬁrst equation has the integral

(u −c)h =−K, (4.97)

where K is a positive constant. The reason that it must be positive is that the posi-

tive characteristics (those with speed u +γh

1/2

) must run into (not away from) the

shock, that is,

+γh

1/2

<c<u

−

+γh

1/2

−

, (4.98)

where h

and h

−

are the values of h immediately in front of and immediately behind

the shock. Hence

γh

3/2

<K<γh

3/2

−

. (4.99)