Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

240 4 River Flow

Fig. 4.7 Laminar roll waves following rainfall at Craggaunowen, Co. Clare, Ireland. The water

depth is a few millimetres and the wavelength of the order of twenty centimetres

Substitution of (4.97) into the second equation yields a single ﬁrst-order equation

for u,orh. We choose to write the equation for h, thus



−(ch −K)

−K

. (4.100)

As indicated in Fig. 4.8, we aim to solve this equation in (0,L), with h = h

ξ =0 and h = h

−

at ξ =L. The quantities involved in this equation and its boundary

conditions are L, c, h

−

, h

and K, and these have to be determined. Solution of the

differential equation (4.100) from 0 to L yields one condition,

L =



−

−K

−(ch −K)

dh, (4.101)

which determines L in terms of the other quantities. Thus four extra conditions need

to be speciﬁed to determine these.

There are two jump conditions to apply across the shock. These are conservation

of mass, which we omit, as it is automatically satisﬁed by (4.97), and conservation

of momentum, which has the form

c =





−

[hu]

−

. (4.102)

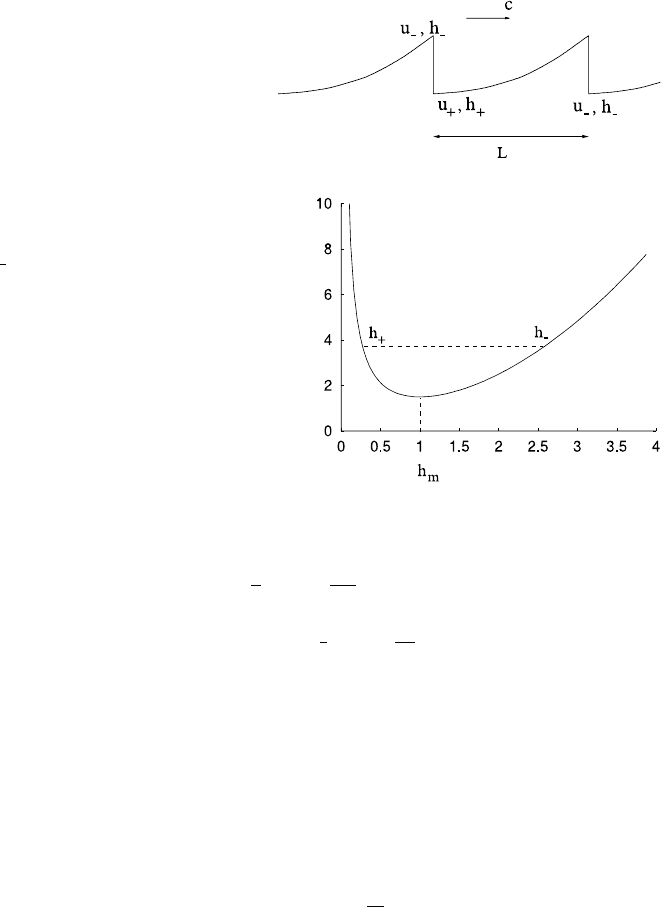
4.5 Nonlinear Waves 241

Fig. 4.8 Schematic form of

roll waves

Fig. 4.9 Supercritical and

subcritical values of h across

a shock: graph of

/h, γ =K =1

Simpliﬁcation of this using (4.97)gives





−

=0. (4.103)

Evidently, consideration of the graph of

shows that this determines h

in terms of h

−

, for given K, see Fig. 4.9.

We denote the critical value of h at the minimum in Fig. 4.9 as h

, thus

; (4.104)

clearly we must have h

−

and h

(this is also implied by (4.99)), that

is to say, the ﬂow is subcritical behind the shock and supercritical in front of it. In

particular, there is a value of ξ ∈(0,L)with h =h

, and in order that the derivative

in (4.100) remain ﬁnite, it is necessary that the numerator also vanish at this point.

Since K>0, this implies

−K =

. (4.105)

We have added an extra quantity h

to the other unknowns L, h

−

, h

, K and

c. To determine these six quantities, we have the four Eqs. (4.101), (4.103), (4.104)

and (4.105). This appears to imply that the roll waves described here form a two pa-

rameter family, with (for example) the wavelength and wave speed being arbitrary.

This is at odds with our expectation that a sensibly described physical problem will

have just the one solution. In order to understand this, we need to reconsider the

242 4 River Flow

hyperbolic form of the describing Eqs. (4.90). A natural domain on which to solve

these equations is the semi-inﬁnite real axis s>0, in which case appropriate bound-

ary conditions are to prescribe h and u on t = 0 and s =0. The initial conditions

are prescribed to represent the experimental start-up, and the boundary conditions

at s = 0 must represent the inlet conditions. The effect of the initial conditions is

washed out of the system as the characteristics progress down stream, and the roll

waves which are observed are determined by the boundary conditions at s =0.

Of course, these inlet conditions are not generally consistent with a periodic trav-

elling wave solution, but we would expect that prescribed values of u and h at the

inlet would provide the extra two parameters to ﬁx the solution precisely. One such

parameter is easy to assess. Because mass is conserved, the mean volume ﬂux must

be equal to that at the inlet, and by choice of the velocity and depth scales, we can

take the volume ﬂux to be one, whence



(ch −K)dξ =1. (4.106)

It is not as obvious how to provide the other recipe, because the mean momentum

ﬂux is not conserved downstream; its value at the inlet does not tell us its value

downstream. This is because of the gravity and friction terms. However, it is the

case that these terms must balance on average, that is to say,





h −u



dξ =0; (4.107)

this actually follows by integrating the momentum equation (written in conservation

form) over a wavelength. The momentum advection and pressure gradient terms

vanish because of (4.103), leaving (4.107). This appears to give a ﬁnal condition to

close the system: but it does not, as (4.107) actually reduces to (4.103) when the

integration is carried out. An appropriate ﬁnal condition is not easy to determine;

we provide some further discussion below. Before that, we reduce the conditions

above to a simpler form.

We rewrite the relations (4.101), (4.103), (4.104), (4.105) and (4.106)usingh

as the deﬁning parameter, and putting

−

; (4.108)

then we have K and c given by

K =γh

3/2

,c=h

1/2

(1 +γ), (4.109)

and L, φ

and φ

−

are determined, after some algebra, by

L =γ



−

(φ

+φ +1)dφ

(φ −γ)

−γ

1 =

5/2



−

(φ

+φ +1){φ +γ(φ−1)}dφ

(φ −γ)

−γ





−

=0,

(4.110)

4.5 Nonlinear Waves 243

where we have taken Q =1in(4.106). The second of these can be written indepen-

dently of L as

q =



−

(φ

+φ+1){φ+γ(φ−1)}dφ

(φ−γ)

−γ



−

(φ

+φ+1)dφ

(φ−γ)

−γ

, (4.111)

where

q =

3/2

. (4.112)

The proﬁle of φ is given by the scaled version of (4.100), which is



(φ −γ)

−γ

(φ

+φ +1)

. (4.113)

The numerator must be positive, and since φ =1forsomeξ, a necessary condition

forthistobetrueisthatγ<1/2. In terms of the Froude number, this is F>2,

which is the condition under which the roll wave instability occurs in the ﬁrst place.

This nicely suggests that the roll waves bifurcate as a non-uniform solution from the

steady state at F =2.

It is apparent from the above discussion that the crux of the determination of the

roll wave parameters is the solution of (4.110)

and (4.111) for given positive q.If

and φ

−

can be found for any such q, then they can be found for any h

,after

which L, K and c follow directly from (4.109) and (4.110)

To ﬁnd the solutions of (4.110)

and (4.111), we note that φ

and φ

−

are

uniquely deﬁned in terms of the ordinate of the graph in Fig. 4.9; in fact, for any

∈(0, 1),(4.110)

gives the explicit solution

−



−φ





1/2



; (4.114)

then (4.111)givesq = q(φ

;γ). The other constants are then given explicitly by

(4.109), (4.110)

and (4.111), and in particular, if we deﬁne

N(φ

) =



−

(φ

+φ +1){φ +γ(φ−1)}dφ

(φ −γ)

−γ

D(φ

) =



−

(φ

+φ +1)dφ

(φ −γ)

−γ

(4.115)

(thus q =N/D), then using





2/3

, (4.116)

we have

L =

5/3

2/3

,c=

(1 +γ)D

1/3

,K=

γD

. (4.117)

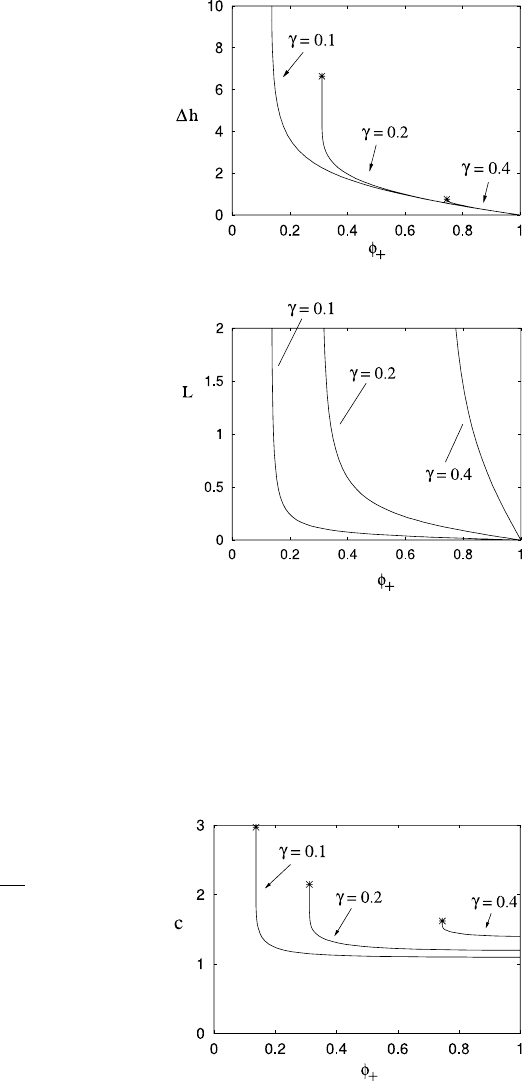
244 4 River Flow

Fig. 4.10 Graphs of

h =h

−

−h

as a function

of φ

for γ = 0.1(F =10),

γ =0.2(F =5) and γ =0.4

(F = 2.5). The asterisks mark

the ends of the curves at

=α

Fig. 4.11 Dimensionless

wavelength L in terms of φ

for γ =0.1(F = 10),

γ =0.2(F =5) and γ =0.4

(F = 2.5). The curves do not

terminate, since

L ∼−ln[φ

−α

] as

→α

Equations (4.114), (4.116) and (4.117) determine φ

−

, h

, L, c and K in terms

of φ

. From these we can ﬁnd h

−

and h

. Thus it is convenient in computing the

one parameter family of wave solutions to use φ

as the parameter.

In Figs. 4.10, 4.11, 4.12 we plot the wave height h =h

(φ

−

−φ

), wavelength

L and speed c (all dimensionless) as a function of the parameter φ

, for various

values of the Froude number F .

Fig. 4.12 Wave speed c in

terms of φ

.Theasterisks

mark the ends of the curves at

=α

, c =c

1+γ

1/3

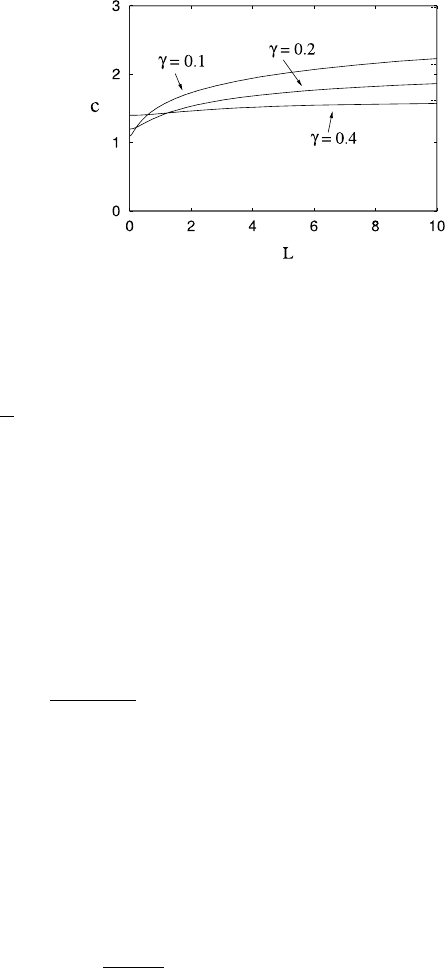
4.5 Nonlinear Waves 245

Fig. 4.13 Wave speed c as a

function of L,forγ = 0.1,

γ =0.2andγ = 0.4. The

short dashed lines at the right

ordinate indicate the

corresponding asymptotes c

for γ =0.1andγ =0.2and

γ =0.4 at the respective

values c

=2.9717, 2.1495,

1.6216

A feature of Fig. 4.10 is the termination of the curves at a ﬁnite value. The inte-

grals which deﬁne N and D in (4.115) can be explicitly evaluated. If we deﬁne the

two (positive) roots of (φ −γ)

−γ

φ =0tobe



2 +γ ±



+4γ



1/2



, (4.118)

thus α

>α

−

> 0, then we restrict φ

>α

so that φ



> 0in(4.113). Consideration

of N and D then shows that

D =−A ln(φ

−α

) +O(1), N =−C ln(φ

−α

) +O(1) (4.119)

as φ →α

. From this it follows that q →q

as φ →α

, where q

=C/A, and is

given explicitly by

=(1 +γ)α

−γ. (4.120)

These termination points are marked by asterisks at the end of the curves in

Fig. 4.10. Because q = q

+O(

−ln(φ

−α

)

), the slope of the curves is inﬁnite at

these points. (This also makes it hard to draw the ﬁgures. To get within 0.02 of q

for example, we can expect to have to take φ

−α

≈exp(−50) ≈10

−22

As φ

→1, then also φ

−

→1, and hence both N and D are O(1). Direct con-

sideration of (4.115) shows that q → 1asφ

→ 1. As a consequence of these

limiting behaviours, L →0 and c is ﬁnite as φ

→1, while L →∞as φ

→α

but c tends to a ﬁnite limit just as q does. As shown in Figs. 4.10–4.12, all three

quantities vary monotonically between φ

= α

and φ

= 1, and consequently c

is a monotonically increasing function of L, which tends to a limit c

as L →∞,

where

(1 +γ)

1/3

. (4.121)

This is shown in Fig. 4.13. Analysis of the limit φ

→ α

shows that c = c

O(1/L) as L →∞(Question 4.15), and evidently the approach to the limit is slow,

particularly at low γ (high Froude number).

246 4 River Flow

Wavelength Selection and Boundary Conditions

Although it is convenient to compute the properties of the roll waves using the pa-

rameter φ

, it is more natural to use the wavelength L as the single parameter. The

issue remains how this is selected. This seems to be an open problem, on which we

offer some comments, though little further insight.

The ﬁrst thing to note is that the hyperbolic St. Venant equations (4.90) require

two initial conditions at the inlet s = 0 if the Froude number F>1. If we imagine

ﬂow from a vent below a dam, for example, it is easy to see that prescription of both

h and hu (and thus u) can be effected, by having a vent opening of a prescribed

height, and adjusting the dam height to control mass ﬂow. From a mathematical

point of view, precisely steady inlet conditions h = u = 1 lead to uniform down-

stream ﬂow, provided the St. Venant equations apply precisely. Thus we can see

that it is only through the prescription of a time varying inlet velocity, for exam-

ple, that roll waves can develop downstream. For example, we might prescribe inlet

conditions

h =1,u=1 +λ cosωt at s =0, (4.122)

where λ  1. We would then infer that the resulting periodic solution would have

frequency ω, and this would prescribe the ratio

=ω, (4.123)

which would provide the ﬁnal prescription of the solution. Consulting Fig. 4.13,we

can see that (4.123) would indeed determine a unique value of L.

More generally, we might suppose u(0,t) to be a polychromatic, perhaps

stochastic function. We might then expect the wavelength selected to be that of

the most rapidly growing mode. Consultation of (4.85), however, indicates that for

F>2, p and thus Reσ is an increasing function of wave number k, with p → F

as k →∞. This unbounded growth at large wave number is suggestive of ill-

posedness, and in any case is certainly not consistent with the apparent observation

that long wavelength roll waves are in practice selected.

A ﬁnal consideration, and perhaps the most practical one, is that wavelength

selection may take place at large times through the interaction of neighbouring wave

crests. Larger waves move more rapidly (c is an increasing function of h if we

plot one in terms of the other), and therefore larger waves will catch smaller ones.

This provides a coarsening effect, whereby smaller waves can be removed by larger

ones. Since h is also an increasing function of L, this coarsening does indeed

lead to longer waves. The process should be limited by the fact that very long (and

thus ﬂat) waves will be subject to the same Vedernikov instability as is the uniform

state.

If we supposed that wavelength varied slowly from wave to wave, we can

see the beginnings of a kind of nonlinear multiple scales method to describe the

evolution of wavelength as a function of space and time. It is less easy to see how

This observation is due to Neil Balmforth.

4.5 Nonlinear Waves 247

to incorporate the generation of new waves in such a framework, however, and this

problem remains open for investigation.

The spectre of ill-posedness described above raises the related issue of how to

prescribe the correct boundary conditions for the St. Venant equations. The reason

there is an issue is that the equations require two upstream boundary conditions if

F>1, but one upstream and one downstream condition if F<1. This makes no

sense, insofar as the boundary conditions should be prescribed independently of the

solution. A resolution of this conundrum lies in the realisation that the formation of

shocks in the hyperbolic system suggests the presence of a missing diffusive term,

and this takes the form of a turbulent eddy viscous term.

In our discussion of the basal friction term (4.5), we assumed only the transverse

Reynolds stress −ρ



≈μ

∂ ¯u

∂z

was signiﬁcant. The longitudinal Reynolds stress

−ρ

2

≈μ

∂ ¯u

∂x

is small, but provides a crucial diffusive term

∂

∂x



∂u

∂x



(4.124)

to be added to the right hand side of (4.43). Following (B.9) in Appendix B,we

suppose

=ρε

[u]d, (4.125)

and this leads to the corrective term

∂

∂x



∂u

∂x



(4.126)

to be added to (4.49)

. Correspondingly, Eqs. (4.90) are modiﬁed to

+(hu)

=0,

+uu

+γ

=γ



1 −



∂

∂s



∂u

∂s



(4.127)

where

κ =ε

S 1. (4.128)

A typical value of κ is ∼10

−5

Because κ is small, it can be expected to provide a shock structure for the shocks

we have described. In addition, the extra derivative suggests that an extra boundary

condition for the system (4.127) needs to be prescribed. Most obviously, this is at

the outlet, where the river meets the sea. The most obvious such condition might be

to prescribe h, or perhaps h

, but it is more likely that one should prescribe

u =0ats =1, (4.129)

indicating the ﬂow of the river into a large reservoir. In any event, the extra condition

at the outlet, together with the diffusive term (4.124), can explain the difference in

the solutions when F ≶ 1. The characteristics of (4.90) are the sub-characteristics

of (4.127), and the appropriate pair of conditions to apply for (4.90) is determined

by the correct way of determining the singular approximation when κ →0.

248 4 River Flow

Fig. 4.14 The Severn bore. This is a famous photograph from 1921, when there were no by-

standers, and certainly no surfers. Reproduced from Pugh (1987). The photograph ﬁrst appears in

the book by Rowbotham (1970), where Mr C.W.F. Chubb is acknowledged as the photographer

However, this really sheds no further light on the issue of roll wave length selec-

tion. When F>2, clearly two conditions are appropriate at s =0, but how these

conspire to select the wavelength is unclear.

4.5.3 Tidal Bores

A bore on a river is a shock-like wave which travels upstream, and it occurs because

of forcing at the mouth of the river due to tidal variation in sea level. In England the

best known example is the Severn bore, which occurs because of the very high tidal

range in the Severn estuary. Large crowds come to view the bore, which manifests

itself as a wall of water about a metre high advancing up river at a speed of some

four to ﬁve metres a second. Figures 4.14 and 4.15 show photographs of the Severn

bore. Bores occur on certain rivers due to a conﬂuence of factors. The tidal range has

to be very large, and this can be caused by tidal resonance in an estuary; in addition,

the river must narrow dramatically upstream, so that the estuary acts like a funnel.

The wave then forms because the rapidly rising water level in the estuary causes a

large upstream water ﬂux, and with a sufﬁciently large funnelling effect, a shock

wave will be formed. Bores occur all over the world, for example in the Amazon,

the Seine, the Petitcodiac river which ﬂows into the Bay of Fundy, and the Tsien

Tang river in China. Where they occur, they are spectacular, but relatively few rivers

have them, because of the severity of the necessary conditions for their formation.

4.5 Nonlinear Waves 249

Fig. 4.15 The Severn bore, viewed from the air in a microlight aircraft by Mark Humpage. The

image is copyright Mark Humpage, and is reproduced with his permission. For other photographs,

see http://www.markhumpage.com. The undular nature of the bore is very clearly visible (as are

the relentless surfers)

Figure 4.16 shows the geometry of the Severn river and estuary. The bore forms

near Sharpness, and is best viewed at various places further upstream, notably Min-

sterworth and Stonebench, where public access is available. Figure 4.17 shows a

proﬁle of the river during passage of a bore. There are certain features evident

in this ﬁgure which are relevant when we formulate a model. The river depth at

low stage is about a metre, whereas the tidal range is much greater than this. In

the Severn estuary, it can be 14.5 metres, and at Sharpness, it is 9 metres in the

ﬁgure. The other feature of importance is the apparent alteration in the bedslope

as the estuary is approached. As an idealisation of this, Fig. 4.18 shows the ba-

sic geometry of a river–estuary system, which we can use to explain bore forma-

tion.

The river in Fig. 4.18 ﬂows into a tidal basin, where the water level ﬂuctuates

tidally with a period of slightly more than twelve hours. Such ﬂuctuations cause

the river/estuary boundary point to migrate back and forth. In particular, approach-

ing high tide this point moves upstream. The idea behind bore formation is that

if the upstream velocity of this boundary is faster than the upstream characteristic