Fowler A. Mathematical Geoscience
Подождите немного. Документ загружается.

250 4 River Flow
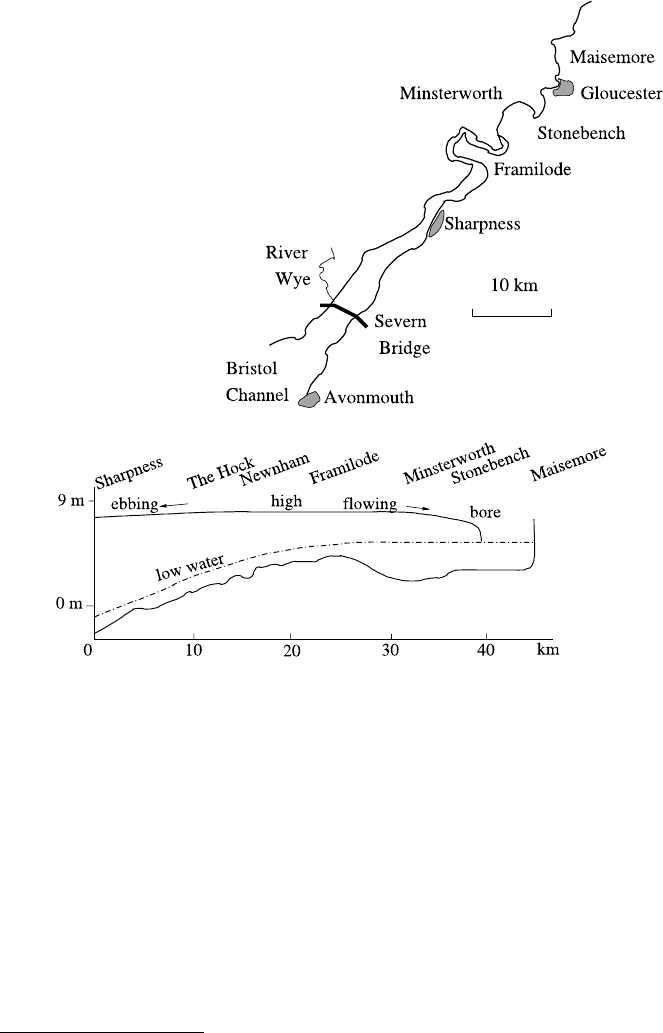
Fig. 4.16 Asketchmapof
the river Severn
Fig. 4.17 Profile of the Severn during passage of a bore. Note that high water occurs someway
below the bore (the tide continues to come in after the passage of the bore), but that the tide near
Sharpness already starts to ebb before the bore reaches Maisemore
wave speed,
5
a smooth wave cannot occur, and a shock must form, as indicated in
Fig. 4.18.
We want to study this phenomenon in the context of the St. Venant equations
(4.49), where for a wide channel, we choose the hydraulic radius and cross sectional
area to be
R =h, A =wh, (4.130)
where w is the width, and is taken to be a prescribed function of s. The phenomenon
of concern occurs over the length of the river, so that long wave theory is appropri-
ate. From Fig. 4.17, a suitable length scale is of the order of 45 km, where the
5
We assume the Froude number F is less than one at low stage, which is the realistic condition; in
that case, one wave travels upstream. If F>1, a standing wave would form at the boundary.
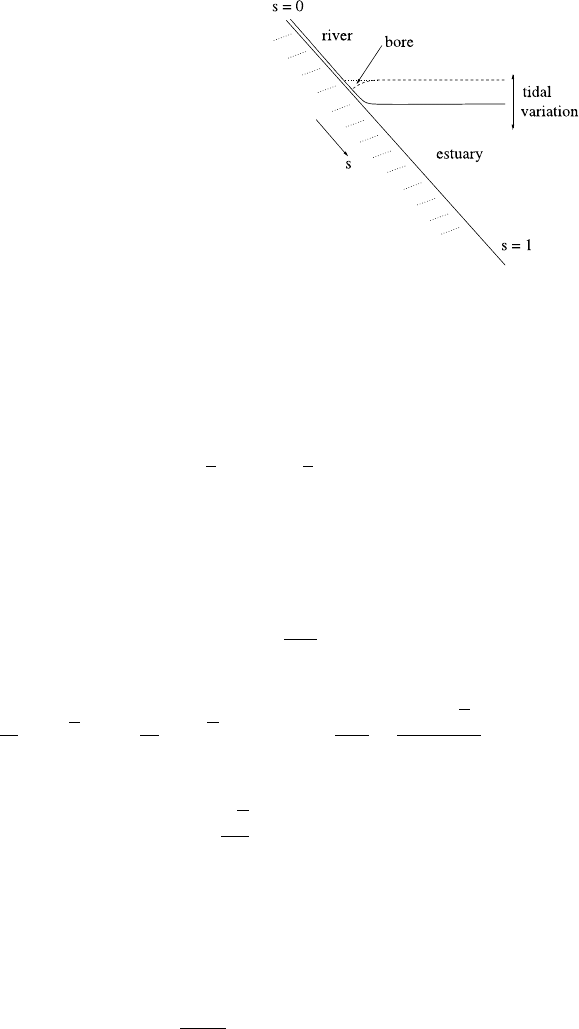
4.5 Nonlinear Waves 251
Fig. 4.18 Idealised (and
highly exaggerated) river
basin geometry
length scale used in writing (4.49)isd/sinα, and is 2 km if we take d =2 m and
S = sin α = 10
−3
. If we take a typical velocity upstream as 2 m s
−1
, then the cor-
responding time scale is 10
3
s, or 15 minutes, and the Froude number is about 0.3.
The scale up in distance is thus of order 22, while that in time to the half-period of
tidal oscillations is similar. This suggests that we rescale both time and space as
t ∼
1
ε
,s∼
1
ε
, (4.131)
where a plausible value of ε may be of order 0.05. In this case (4.49) can be writ-
ten in the form (where now, because u will be negative during inflow, we take the
friction term in the corrected form ∝|u|u)
wh
t
+(wuh)
s
=0,
εF
2
(u
t
+uu
s
) =1 −
|u|u
h
−εh
s
,
(4.132)
or equivalently in the form
ε
±F
∂
∂t
+
√
h ±Fu
∂
∂s
2
√
h ±Fu
=1 −
|u|u
h
∓
εFw
√
hu
w
, (4.133)
which shows explicitly that the characteristic wave speeds are
±
√
h
F
+u, (4.134)
as we found before. Finally, we wish to study the situation shown in Fig. 4.18, where
the tidal range is significantly larger than the river depth. The simplest choice is to
suppose the tidal amplitude is also O(1/ε), so that appropriate boundary conditions
for (4.132)are
wuh =1ats =0,
h =
H
1
(t)
ε
at s =1,
(4.135)
representing a constant upstream volume flux, and a prescribed tidal range.

252 4 River Flow
The assumption that ε 1 allows us to solve (4.132) asymptotically. The solu-
tion has two parts, river and estuary, joined at a front which we denote by s =s
f
.
Upstream, for s<s
f
, the flow is quasi-stationary, and we have, to leading order,
wuh ≈1, 1 −
u|u|
h
≈1, (4.136)
whence
u ≈w
−1/3
,h=w
−2/3
. (4.137)
The steady solution of (4.132) is appropriate, because the sub-characteristic wave
propagates downstream, and after any initial transient, the upstream boundary con-
dition leads to a steady flow.
Downstream, for s>s
f
, we write
h =
H
ε
, (4.138)
so that
wH
t
+(wuH )
s
≈0,
1 −H
s
≈0
(4.139)
(the surface is flat); from this we have
H ≈s −1 +H
1
(t), (4.140)
and from this there follows
u ≈
−
˙
H
1
s
s
f
wds
wH
, (4.141)
where we choose the integration constant for matching purposes at s
f
.Alsotomatch
the solution to that in s<s
f
, we need to take
s
f
=1 −H
1
. (4.142)
Transition Region
At the front, we define
s =s
f
+εX, ˙s
f
=c, w
f
=w
s
f
(t)
; (4.143)
then to leading order we have
−cw
f
h
X
+(w
f
hu)
X
=0,
F
2
(u −c)u
X
=1 −
u|u|
h
−h
X
,
(4.144)
with boundary conditions
h →h
−
=w
−2/3
f
,u→u
−
=w
−1/3
f
as X →−∞,
h ∼X, u ∼c as X →∞,
(4.145)

4.5 Nonlinear Waves 253
in order to match to the upstream and downstream solutions. Note that this transition
region, like that for the monoclinal flood wave, is mediated by the full St. Venant
equations, but without a diffusive term. Only the conditions on h in (4.145) are nec-
essary, those on u following automatically. A first integral of the mass conservation
equation (4.144)
1
gives
(u −c)h =K =
w
−1/3
f
−c
w
−2/3
f
, (4.146)
and from this we find
h
X
=
h
3
−|K +ch|(K +ch)
h
3
−K
2
F
2
. (4.147)
This can be compared with (4.100). The difference in the present case is that c and
K in (4.143) and (4.146) are given, and the question is only whether a solution exists
joining h = h
−
=w
−2/3
f
upstream to the downstream solution h ∼X. Note that as
X →−∞, K +ch →w
−1
f
, so that h →w
−2/3
f
can consistently be satisfied.
Let us suppose that the tide is coming in, thus c<0. We suspect that a smooth
solution in the transition region may not be possible if −c is greater than the up-
stream wave speed. Using (4.134) and (4.145), this condition can be written in the
form
−c>w
−1/3
f
1
F
−1
(4.148)
(assuming F<1). If we suppose that the opposite inequality holds, i.e., −c<
w
−1/3
f
(
1
F
−1), then a little algebra shows that this is precisely the criterion that
h
−
=w
−2/3
f
>(KF)
2/3
, (4.149)
i.e., the denominator of (4.147) is positive. To see that there is a solution of this
problem in this case, we need to show that the numerator of the right hand side
(4.147) is also positive, for then h will increase indefinitely as required.
The numerator, N , is given by
N =
h
3
−w
−2
f
−
w
−1
f
+c
h −w
−2/3
f
w
−1
f
+c
h −w
−2/3
f
−w
−2
f
.
(4.150)
Both expressions in curly brackets are zero when h =h
−
at X =−∞;forh slightly
greater than h
−
, the left curly bracketed expression is positive, while the right curly
bracketed expression decreases, since c<0. The numerator is thus positive for
h −h
−
small and positive, and remains so. From this it follows that a solution of
the transition problem exists if −c<w
−1/3
f
(
1
F
−1), and thus a bore will not form.
It remains to be shown that no solution exists if the opposite inequality, (4.148),
holds. In this case the denominator of the right hand side of (4.147) is initially
negative. As before, the numerator is positive if h>h
−
, and equivalently negative
if h<h
−
, thus implying h
X
< 0ifh>h
−
, and h
X
> 0ifh<h
−
. This means
solutions of (4.147) can only approach h
−
as X →∞, and no transition solution

254 4 River Flow
Fig. 4.19 Bore formation occurs for large tides and rapidly widening rivers with reasonably sized
Froude numbers. If the tide oscillates sinusoidally and the river slope is constant, then the front
position s
f
will trace an ellipse as shown in the (s
f
, ˙s
f
) plane. For a funnel-shaped river, the width
w decreases as s
f
decreases, so that (
1
F
−1)w
−1/3
is a decreasing function of s
f
,asshown.Bore
formation therefore occurs according to (4.148) for the solid tidal curve, but not for the smaller
amplitude dotted one
exists. This suggests another form of solution, one in which a discontinuity forms at
the critical condition
−˙s
f
=w(s
f
)
−1/3
1
F
−1
, (4.151)
and thereafter propagates upstream as a shock front. This is the bore. Figure 4.19
shows a schematic illustration of the criterion (4.151) for bore formation.
Propagation of the Bore
The outer river and estuary solutions (4.137), (4.140) and (4.141) remain valid after
the formation of a shock, but the transition region is replaced by a shock at s
f
, where
the values of h
−
and u
−
(given by (4.137) with w = w
f
) jump (up) to values h
+
and u
+
, which have to be determined along with s
f
. Initially h
+
and u
+
are O(1),
and we anticipate that this remains true; in this case s
f
is still given by
s
f
=1 −H
1
+O(ε); (4.152)
the location of the bore is essentially determined by the tidal range. Jump conditions
of mass and momentum across the developing bore then imply that the bore speed
˙s
f
=c satisfies
c =
[hu]
+
−
[h]
+
−
=
1
2
[h
2
]
+
−
+F
2
[hu
2
]
+
−
[hu]
+
−
, (4.153)
and these two relations serve to determine h
+
and u
+
, since c =−
˙
H
1
.

4.5 Nonlinear Waves 255
Shock Structure
We can use the transition equations (4.144), modified by the addition of the diffusive
term in (4.127), to study the shock structure of the bore. The equations then take the
form
−cw
f
h
X
+(w
f
hu)
X
=0,
F
2
(u −c)u
X
=1 −
u|u|
h
−h
X
+
κF
2
h
∂
∂X
h
∂u
∂X
,
(4.154)
and the boundary conditions are still (4.145). The difference with the preceding
analysis is that when a bore forms, we expect the diffusive term to act as a singular
perturbation which allows the matching of two distinct outer solutions through an
interior shock (the bore). Writing
u =c +
K
h
, (4.155)
we find that h satisfies
∂h
∂X
=
h
3
−|K +ch|(K +ch)
h
3
−K
2
F
2
−
κF
2
Kh
2
h
3
−K
2
F
2
∂
∂X
1
h
∂h
∂X
. (4.156)
As discussed before (4.151), the only way h can approach h
−
as X →−∞in
bore-forming conditions is if the outer solution (where κ =0) in X<0is
h ≡h
−
,X<0. (4.157)
We suppose that h jumps through the shock to a value h
+
>h
−
. According to
the argument following (4.150), the numerator of (4.147) for the outer solution in
X>0 is then positive, and so, providing h
3
+
>K
2
F
2
, the outer solution for h will
increase monotonely from h
+
, and h ∼X as X →∞. It only remains to show that
a shock structure exists connecting h
−
to h
+
>(KF)
2/3
.
Supposing without loss of generality the shock to be at X =0, we define
X =κKF
2
ξ (4.158)
(noting that K>0), so that to leading order (4.156) becomes
∂h
∂ξ
=−
h
2
h
3
−K
2
F
2
∂
∂ξ
1
h
∂h
∂ξ
. (4.159)
Integrating this, we find
∂h
∂ξ
=−h
1
2
h
2
−h
2
−
+K
2
F
2
1
h
−
1
h
−
. (4.160)
Consideration of the right hand side of this equation shows that if h
3
−
<K
2
F
2
,
then −
h
h
is zero at h =h
−
, negative for h>h
−
until it becomes positive for large
h. Thus there is one further zero of h
at h
+
>h
−
, and h
> 0 between these two
values, always assuming that h
3
−
<K
2
F
2
, which is guaranteed by (4.149). Thus the
shock layer structure takes h monotonically from h
−
to h
+
, given by
1
2
h
2
+
−h
2
−
=K
2
F
2
1
h
−
−
1
h
+
, (4.161)

256 4 River Flow
and it only remains to check that h
+
>(KF)
2/3
, so that the outer solution to (4.147)
in X>0 does indeed increase as X →∞. This is clear from the definition of −
h
h
given by (4.160), which shows that −
h
h
is a convex upwards function G(h), and in
particular shows that G
(h
+
)>0. Since from (4.159),
G
(h) =
h
3
−K
2
F
2
h
2
, (4.162)
we can deduce that indeed h
+
>(KF)
2/3
.
This analysis shows that in bore-forming conditions, the diffusive term in (4.154)
does indeed allow a shock structure to exist, and this describes what is known as a
turbulent bore, appropriate at reasonably large Froude numbers. The Severn bore
showninFig.4.15 is an example of an undular bore, appropriate at lower Froude
numbers, and consisting of an oscillatory wave train. The St. Venant equations do
not appear to be able to describe this kind of bore, where the oscillations have a
wavelength comparable to the depth, and the vertical velocity structure may need to
be considered in attempting to model it. This is discussed further below.
4.6 Notes and References
A preliminary version of the material in this chapter is in my own book on modelling
(Fowler 1997), although with much less detail than presented here. The general
subject of river flow is treated in its contextual, geographical aspect by books on
hydrology, such as those of Chorley (1969) or Ward and Robinson (2000). Ward and
Robinson’s book, for example, deals with precipitation, evaporation, groundwater
and other topics as well as the dynamics of drainage basins, but is less concerned
with detailed flow processes in rivers. For these, we turn to books on hydraulics,
such as those by French (1994)orChow(1959). A nice book, which bridges the
gap, and also includes a discussion of sediment transport and channel morphology
and pattern, is that by Richards (1982).
Roll Waves Flood waves and roll waves have been discussed from the present
perspective by Whitham (1974). The linear instability at Froude number greater than
two was analysed by Jeffreys (1925), and the finite amplitude form of roll waves
was described by Dressler (1949), whose presentation we follow here. The book by
Stoker (1957) gives a nice discussion, as well as a useful photograph of roll waves
on a spillway in Switzerland. The eddy viscous diffusive term in (4.127) was added
by Needham and Merkin (1984). Balmforth and Mandre (2004) provide a thorough
review, and also provide a discussion of the mechanics of wavelength selection.
They also, following Yu and Kevorkian (1992), provide a weakly nonlinear model
for roll wave evolution when F −2 1; a strongly nonlinear model would be more
relevant at higher F . Their experiments are consistent with the idea that the form of
the inlet condition is instrumental in determining the roll wavelength.

4.6 Notes and References 257
Tidal Bores The effect of tidal variations on river flow is discussed by Pugh
(1987); in particular, he describes the phenomenon of the river bore. Another use-
ful little book is that by Tricker (1965). The literature on bores seems to be rather
sparse, although the phenomenon itself has been well known for a (very) long time.
Chanson (2005) refers to the fact that the mascaret of the Seine river in France was
documented in the ninth century. Lord Rayleigh, while president of the Royal So-
ciety, wrote down the jump conditions for the bore velocity over a hundred years
ago (Rayleigh 1908). There is a very informative article by Lynch (1982), prior to
which the principal analysis is that of Abbott and Lighthill (1956), who analyse the
St. Venant equations, and apply their results to the Severn bore. The presentation is
extremely opaque, however. The little book by Rowbotham (1970) is a gem, and has
many other striking photographs besides that shown in Fig. 4.14.
More recently, there has been an upsurge of interest in modelling bores. Su et al.
(2001) construct a numerical model of the turbulent bore of the Hangzhou Gulf and
Qiantangjiang river in China using the St. Venant equations. In a number of papers,
Chanson and co-workers have studied the dynamics of undular bores (Wolanski et
al. 2004; Chanson 2005), both observationally and experimentally. Chanson (2009)
reviews the observational and experimental literature, with numerous illustrations.
In order to obtain an oscillatory wave train (such as one also finds in capillary
waves), it seems that a higher derivative term in (4.160) might be necessary, either
as h
ξξξ
or from a term u
XXX
in (4.154). Such terms are commonly found in higher-
order approximations to water wave equations, as for example in the Korteweg–de
Vries equation. To get a flavour of such an analysis, we consult the derivation of
the Korteweg–de Vries equation by Ockendon and Ockendon (2004, pp. 106 ff.).
Reverting to dimensional coordinates, their derivation of the Korteweg–de Vries
equation takes the form, assuming a backwards travelling wave,
u
t
+···=
√
gd d
2
6
u
sss
. (4.163)
If we simply suppose that such a term can be added to the St. Venant equation, then,
using the scales in (4.48), the St. Venant equations (4.50)or(4.127) become
wh
t
+(wuh)
s
=0,
F
2
(u
t
+uu
s
) +h
s
=1 −
|u|u
h
+
κF
2
h
∂
∂s
h
∂u
∂s
+
1
6
FS
2
u
sss
.
(4.164)
Repeating the shock structure analysis, (4.156) is replaced by
−
1
6
FKS
2
1
h
XXX
+κF
2
Kh
2
h
X
h
+P(h)h
X
−N(h)=0, (4.165)
where
P(h)=h
3
−K
2
F
2
,N(h)=h
3
−|K +ch|(K +ch) (4.166)
(N(h) is the numerator in (4.147) discussed following (4.150)).
We write
h =h
−
φ, N =h
3
−
n(φ), P =h
3
−
p(φ), c =−
h
−
V, (4.167)
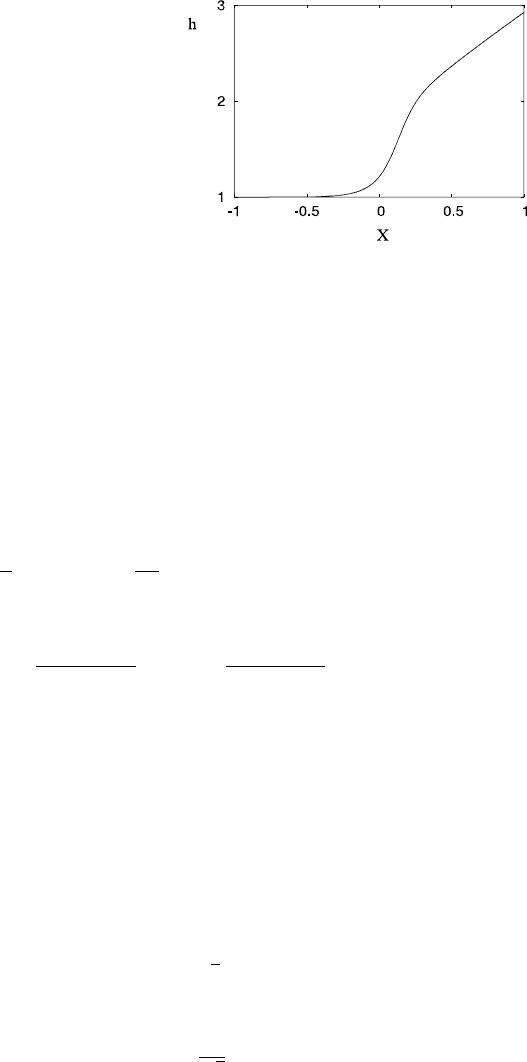
258 4 River Flow
Fig. 4.20 Model of a
turbulent bore. Solution of
(4.165) in the form (4.171),
using values F =1.5, V =0,
β =0.1, δ =0.01. The time
step used is 10
−5
,andthe
plot takes h
−
=1 in its scales
for X and h
whence (4.145) and (4.146)imply
K =h
3/2
−
(1 +V), (4.168)
and hence
n(φ) =φ
3
−|1 +V −Vφ|(1 +V −Vφ), p(φ)=φ
3
−(1 +V)
2
F
2
. (4.169)
Lastly we put
X =h
−
Z. (4.170)
Then (4.165) becomes
−δ
1
φ
ZZZ
+βφ
2
φ
Z
φ
Z
+p(φ)φ
Z
−n(φ) =0, (4.171)
where
δ =
F(1 +V)S
2
6h
11/2
−
,β=
κF
2
(1 +V)
h
3/2
−
, (4.172)
and both are small.
The boundary conditions for φ are that
φ →1asZ →−∞,φ∼ Z as Z →∞. (4.173)
Figures 4.20 and 4.21 show numerical solutions of the transition equation (4.171)
for two different values of β. The first corresponds to a relatively high value of β,
when δ is sufficiently small to be ignored, and the preceding shock structure analysis
(following (4.154)) is valid. Formally this requires δ β
2
.
At lower values of β, however, it is inadmissible to neglect the third derivative
term. To analyse what happens in this case, write
Z =
√
δζ, (4.174)
and define
μ =
β
√
δ
. (4.175)
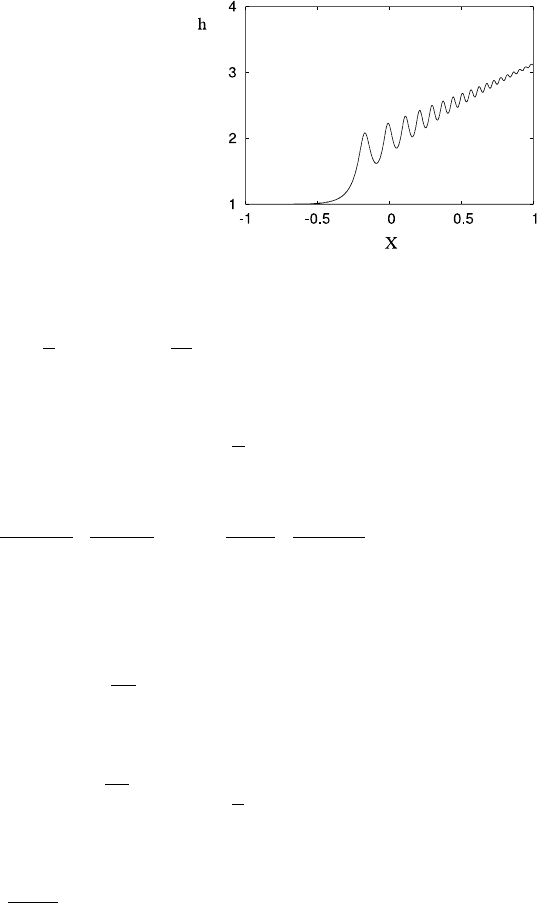
4.6 Notes and References 259
Fig. 4.21 Model of an
undular bore. Solution as for
Fig. 4.20, except that
β =0.001
Assuming δ 1, we can neglect the term in n within the transition zone, so that
−
1
φ
ζζζ
+μφ
2
φ
ζ
φ
ζ
+p(φ)φ
ζ
≈0. (4.176)
The turbulent bore is regained if μ 1. For the case μ 1, define
ψ =1 −
1
φ
, (4.177)
whence
ψ
+
μ
(1 −ψ)
2
ψ
(1 −ψ)
+p
1
1 −ψ
ψ
(1 −ψ)
2
=0. (4.178)
Suppose first that μ is small; then a first integral of (4.178) with μ =0is
ψ
+W
(ψ) =0, (4.179)
where
W
(ψ) =
1
1−ψ
1
p(φ) dφ, W(0) =0. (4.180)
Integrating and changing the order of integration, we can write
W(ψ)=
1
1−ψ
1
ψ −
1 −
1
φ
p(φ) dφ. (4.181)
As a function of ψ , W(0) = W
(0) = 0, and (since p(1)<0, equivalent to the
bore-forming condition (4.148)) W
(0)<0; thus W is negative for small ψ>0.
Since W
(ψ) =
p(φ)
(1−ψ)
2
, and p is an increasing function of φ, we see that W reaches
a negative minimum, and thereafter increases, tending towards ∞ as ψ → 1 and
φ →∞.
(4.179) is the equation of a nonlinear oscillator, and shows that φ increases from
zero at Z =−∞, and then oscillates about the minimum of W . In fact with μ =0,
there would be precisely one oscillation, with φ returning to zero at Z =+∞.This
does not happen for two reasons. The term in μ is a damping term (this is clear
in (4.176) if the coefficient φ
2
is ignored; alternatively one can view (4.176)asa
