Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

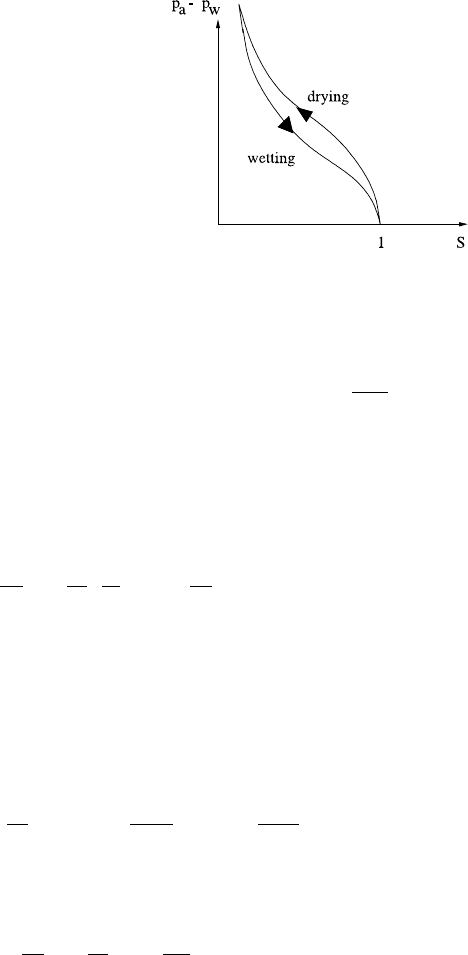
400 7 Groundwater Flow

Fig. 7.4 Capillary suction

characteristic. It displays

hysteresis in wetting and

drying

where

k is a unit vector upwards, and the permeability k depends on S.Ifk(1) =k

(the saturated permeability), then one commonly writes k = k

(S), where k

is the relative permeability. The most obvious assumption would be k

= S,but

this is rarely appropriate, and a better representation is a convex function, such as

. An even better representation is a function such as k

S−S

1−S

)

, where

is known as the residual saturation. It represents the fact that in ﬁne-grained

soils, there is usually some minimal water fraction which cannot be removed. It is

naturally associated with a capillary suction characteristic function p

−p =f(S)

which tends to inﬁnity as S →S

+, also appropriate for ﬁne-grained soils.

In one dimension, and if we take the vertical coordinate z to point downwards,

we obtain the Richards equation

∂S

∂t

=−

∂

∂z



(S)



∂f

∂z

+ρg



. (7.56)

We are assuming p

= constant (and also that the soil matrix is incompressible).

7.3.2 Non-dimensionalisation

We choose scales for the variables as follows:

f =

ψ, z ∼

ρgd

,t∼

φμz

ρgk

, (7.57)

where d

is grain size and σ is the surface tension, assumed constant. The Richards

equation then becomes, in dimensionless variables,

∂S

∂t

=−

∂

∂z





∂ψ

∂z



. (7.58)

To be speciﬁc, we consider the case of soil wetting due to surface inﬁltration: of

rainfall, for example. Suitable boundary conditions for inﬁltration are

S =1atz =0 (7.59)

7.3 Unsaturated Soils 401

if surface water is ponded, or



∂ψ

∂z



∗

μu

, (7.60)

if there is a prescribed downward ﬂux u

; K

is the saturated hydraulic conduc-

tivity. In a dry soil we would have S → 0asz →∞,orifthereisawatertable

at z = z

, S = 1 there.

For silt with k

= 10

−14

, the hydraulic conductivity

∼ 10

−7

−1

or 3 m y

−1

, while average rainfall in England, for example, is

≤1my

−1

. Thus on average u

∗

≤ 1, but during storms we can expect u

∗

 1. For

large values of u

∗

, the desired solution may have S>1atz =0; in this case ponding

occurs (as one observes), and (7.60) is replaced by (7.59), with the pond depth being

determined by the balance between accumulation, inﬁltration, and surface run-off.

7.3.3 Snow Melting

An application of the unsaturated ﬂow model occurs in the study of melting snow.

In particular, it is found that pollutants which may be uniformly distributed in snow

(e.g. SO

from sulphur emissions via acid rain) can be concentrated in melt wa-

ter run-off, with a consequent enhanced detrimental effect on stream pollution. The

question then arises, why this should be so. We shall ﬁnd that uniform surface melt-

ing of a dry snowpack can lead to a meltwater spike at depth.

Suppose we have a snow pack of depth d. Snow is a porous aggregate of ice

crystals, and meltwater formed at the surface can percolate through the snow pack

to the base, where run-off occurs. (We ignore effects of re-freezing of meltwater.)

The model (7.58) is appropriate, but the relevant length scale is d. Therefore we

deﬁne a parameter

κ =

ρgdd

, (7.61)

and we rescale the variables as z ∼1/κ, t ∼1/κ. To be speciﬁc, we will also take

, (7.62)

and

ψ(S)=

−S, (7.63)

based on typical experimental results.

Suitable boundary conditions in a melting event might be to prescribe the melt

ﬂux u

at the surface, thus



∂ψ

∂z



∗

at z =0. (7.64)

With constant air pressure, continuity of S follows from continuity of pore water pressure.

402 7 Groundwater Flow

If the base is impermeable, then



∂ψ

∂z



=0atz =h. (7.65)

This is certainly not realistic if S reaches 1 at the base, since then ponding must

occur and presumably melt drainage will occur via a channelised ﬂow, but we ex-

amine the initial stages of the ﬂow using (7.65). Finally, we suppose S =0att =0.

Again, this is not realistic in the model (it implies inﬁnite capillary suction) but it is

a feasible approximation to make.

Simpliﬁcation of this model now leads to the dimensionless Darcy–Richards

equation in the form

∂S

∂t

+3S

∂S

∂z

=κ

∂

∂z





1 +S



∂S

∂z



. (7.66)

If we choose σ = 70 mN m

−1

, d

= 0.1 mm, ρ = 10

kg m

−3

, g = 10 m s

−2

d = 1 m, then κ = 0.07. It follows that (7.66) has a propensity to form shocks,

these being diffused by the term in κ over a distance O(κ) (by analogy with the

shock structure for the Burgers equation, see Chap. 1).

We want to solve (7.66) with the initial condition

S =0att =0, (7.67)

and the boundary conditions

−κS



1 +S



∂S

∂z

∗

on z =0, (7.68)

and

−κS



1 +S



∂S

∂z

=0atz =1. (7.69)

Roughly, for κ 1, these are

S =S

at z =0,

S =0atz =1,

(7.70)

where S

∗1/3

, which we initially take to be O(1) (and <1, so that surface pond-

ing does not occur).

Neglecting κ, the solution is the step function

S =S

,z<z

S =0,z>z

(7.71)

and the shock front at z

advances at a rate ˙z

given by the jump condition

˙z

]

−

[S]

−

. (7.72)

7.3 Unsaturated Soils 403

Fig. 7.5 S(Z) given by

(7.78); the shock front

terminates at the origin

In dimensional terms, the shock front moves at speed u

/φS

, which is in fact ob-

vious (given that it has constant S behind it).

The shock structure is similar to that of Burgers’ equation. We put

z =z

+κZ, (7.73)

and S rapidly approaches the quasi-steady solution S(Z) of

−VS



+3S







1 +S









, (7.74)

where V =˙z

; hence



1 +S





=−S



−S



, (7.75)

in order that S →S

as Z →−∞, and where we have chosen

V =S

, (7.76)

(as S

=0), thus reproducing (7.72). The solution is a quadrature,



(1 +S

)dS

−S

)

=−Z, (7.77)

with an arbitrary added constant (amounting to an origin shift for Z). Hence

S −

(1 +S

)



−S



=Z. (7.78)

The shock structure is shown in Fig. 7.5; the proﬁle terminates where S = 0at

Z = 0. In fact, (7.75) implies that S = 0or(7.78) applies. Thus when S given by

(7.78) reaches zero, the solution switches to S = 0. The fact that ∂S/∂Z is discon-

tinuous is not a problem because the diffusivity S(1 +S

) goes to zero when S =0.

This degeneracy of the equation is a signpost for fronts with discontinuous deriva-

tives: essentially, the proﬁle can maintain discontinuous gradients at S = 0 because

the diffusivity is zero there, and there is no mechanism to smooth the jump away.

Suppose now that k

= 10

−10

and μ/ρ = 10

−6

−1

; then the satu-

rated hydraulic conductivity K

= k

ρg/μ = 10

−3

−1

. On the other hand, if

404 7 Groundwater Flow

a metre thick snow pack melts in ten days, this implies u

∼ 10

−6

−1

. Thus

∼10

−3

, and the approximation S ≈S

looks less realistic. With

−κS



1 +S



∂S

∂z

, (7.79)

and S

∼10

−1

and κ ∼10

−1

, it seems that one should assume S 1. We deﬁne

S =





1/2

s; (7.80)

(7.79) becomes

βs

−s



1 +



∂s

∂z

=1onz =0, (7.81)

and we have S

/κ ∼10

−2

, β =(S

/κ)

3/2

∼1.

We neglect the term in S

/κ, so that

βs

−s

∂s

∂z

≈1onz =0, (7.82)

and substituting (7.80)into(7.66) leads to

∂s

∂τ

+3βs

∂s

∂z

≈

∂

∂z



∂s

∂z



, (7.83)

if we deﬁne t = τ/(κS

)

1/2

. A simple analytic solution is no longer possible, but

the development of the solution will be similar. The ﬂux condition (7.82)atz = 0

allows the surface saturation to build up gradually, and a shock will only form if

β 1 (when the preceding solution becomes valid).

7.3.4 Similarity Solutions

If, on the other hand, β 1, then the saturation proﬁle approximately satisﬁes

∂s

∂τ

∂

∂z



∂s

∂z



−s

∂s

∂z



1onz =0,

0onz =1.

(7.84)

At least for small times, the model admits a similarity solution of the form

s =τ

f(η), η=z/τ

, (7.85)

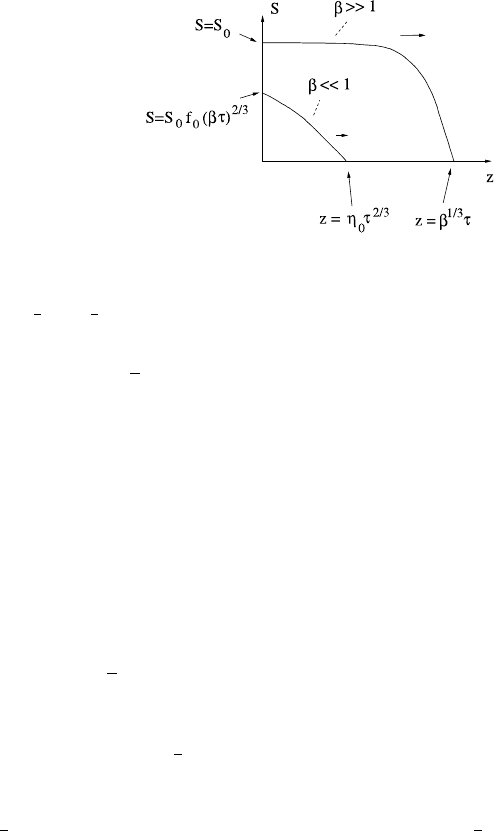
7.3 Unsaturated Soils 405

Fig. 7.6 Schematic

representation of the

evolution of S for both large

and small β

where satisfaction of the equations and boundary conditions requires 2a = b and

2b =1 =a, whence a =

, b =

, and f satisﬁes

(ff



)



−

(f −2ηf



) =0, (7.86)

with the condition at z =0 becoming

−ff



=1atη =0. (7.87)

The condition at z = 1 can be satisﬁed for small enough τ, as we shall see, be-

cause Eq. (7.86) is degenerate, and f reaches zero in a ﬁnite distance, η

, say, and

f =0forη>η

.Asη =1/τ

2/3

at z =1, then this solution will satisfy the no ﬂux

condition at z =1 as long as τ<η

−3/2

, when the advancing front will reach z =1.

To see why f behaves in this way, integrate once to ﬁnd







=−1 +



fdη. (7.88)

For small η, the right hand side is negative, and f is positive (to make physical

sense), so f decreases (and in fact f



< −

η). For sufﬁciently small f(0) = f

, f

will reach zero at a ﬁnite distance η = η

, and the solution must terminate. On the

other hand, for sufﬁciently large f



fdηreaches 1 at η = η

while f is still

positive (and f



=−

there). For η>η

, then f remains positive and f



> −

(f cannot reach zero for η>η

since



fdη>1forη>η

). Eventually f must

have a minimum and thereafter increase with η. This is also unphysical, so we re-

quire f to reach zero at η = η

. This will occur for a range of f

, and we have to

select f

in order that



fdη=1, (7.89)

which in fact represents global conservation of mass. Figure 7.6 shows the schematic

form of solution both for β 1 and β  1. Evidently the solution for β ∼ 1 will

have a proﬁle with a travelling front between these two end cases.

406 7 Groundwater Flow

7.4 Immiscible Two-Phase Flows: The Buckley–Leverett

Equation

In some circumstances, the ﬂow of more than one phase in a porous medium is

important. The type example is the ﬂow of oil and gas, or oil and water (or all three!)

in a sedimentary basin, such as that beneath the North Sea. Suppose there are two

phases; denote the phases by subscripts 1 and 2, with ﬂuid 2 being the wetting ﬂuid,

and S is its saturation. Then the capillary suction characteristic is

−p

(S), (7.90)

with the capillary suction p

being a positive, monotonically decreasing function of

saturation S; mass conservation takes the form

−φ

∂S

∂t

+∇.u

=0,

∂S

∂t

+∇.u

=0,

(7.91)

where φ is (constant) porosity, and Darcy’s law for each phase is

=−

[∇p

+ρ

k],

=−

[∇p

+ρ

k],

(7.92)

with k

being the relative permeability of ﬂuid i.

For example, if we consider a one-dimensional ﬂow, with z pointing upwards,

then we can integrate (7.91) to yield the total ﬂux

=q(t). (7.93)

If we deﬁne the mobilities of each ﬂuid as

, (7.94)

then it is straightforward to derive the equation for S,

∂S

∂t

=−

∂

∂z



eff



∂p

∂z

+(ρ

−ρ



, (7.95)

where the effective mobility is determined by

eff





−1

. (7.96)

7.4 Immiscible Two-Phase Flows: The Buckley–Leverett Equation 407

Fig. 7.7 Graph of

dimensionless wave speed

V(S)as a function of wetting

ﬂuid saturation, indicating the

speed and direction of wave

motion (V>0 means waves

move upwards) if the wetting

ﬂuid is more dense. The

viscosity ratio μ

(see

(7.100))istakentobe30

This is a convective-diffusion equation for S. If suction is very small, we obtain

the Buckley–Leverett equation

∂S

∂t

∂

∂z



eff



+(ρ

−ρ



=0, (7.97)

which is a nonlinear hyperbolic wave equation. As a typical situation, suppose

q =0, and k

, k

=(1 −S)

. Then

eff

(1 −S)

+μ

(1 −S)

, (7.98)

and the wave speed v(S) is given by

v =−(ρ

−ρ

)gM



eff

(S) =v

V(S), (7.99)

where

(ρ

−ρ

)gk

,V(S)=



(S)

χ(S)

χ(S)=

(1 −S)

,μ

(7.100)

The variation of V with S is shown in Fig. 7.7.Forρ

>ρ

(as for oil and water,

where water is the wetting phase), waves move upwards at low water saturation and

downwards at high saturation.

Shocks will form, but these are smoothed by the diffusion term −

∂

∂z

eff



∂S

∂z

in which the diffusion coefﬁcient is

D =−M

eff



. (7.101)

As a typical example, take

(1 −S)

(7.102)

408 7 Groundwater Flow

with λ

> 0. Then we ﬁnd

D =k

2−λ

(1 −S)

2+λ



S +λ

(1 −S)

+μ

(1 −S)



, (7.103)

and we see that D is typically degenerate at S = 0. In particular, if λ

< 2, then

inﬁltration of the wetting phase into the non-wetting phase proceeds at a ﬁnite rate,

and this always occurs for inﬁltration of the non-wetting phase into the wetting

phase.

A particular limiting case is when one phase is much less dense than the other,

the usual situation being that of gas and liquid. This is exempliﬁed by the problem

of snow-melt run-off considered earlier. In that case, water is the wetting phase, thus

−ρ

= ρ

−ρ

is positive, and also μ

≈ 10

−3

Pa s, μ

≈ 10

−5

Pa s, whence

μ

(μ

1), so that, from (7.98),

eff

≈

, (7.104)

at least for saturations not close to unity. Shocks form and propagate downwards

(since ρ

>ρ

). The presence of non-zero ﬂux q<0 does not affect this statement.

Interestingly, the approximation (7.104) will always break down at sufﬁciently high

saturation. Inspection of V(S) for μ

= 0.01 (as for air and water) indicates that

(7.104) is an excellent approximation for S  0.5, but not for S  0.6; for S  0.76,

V is positive and waves move upwards. As μ

→0, the right hand hump in Fig. 7.7

moves towards S = 1, but does not disappear; indeed the value of the maximum

increases, and is V ∼ μ

−1/3

. Thus the single phase approximation for unsaturated

ﬂow is a singular approximation when μ

1 and 1 −S 1.

7.5 Heterogeneous Porous Media

Perhaps the major concern in groundwater studies concerns the permeability.

Whereas we tend to think of the permeability as a well-deﬁned quantity which re-

ﬂects the local soil or rock properties, in reality it varies over many orders of mag-

nitude on very small length scales. The consequence of this is that the value of the

permeability itself needs to be averaged in some way.

Permeability is so variable because of soil and rock heterogeneity. Because it

scales with the square of the constituent grain size, clay and sand permeabilities are

vastly different. And because sediments are lain down so slowly, over millions of

years, sand and clay layers often lie in close proximity. The same is true for sedi-

mentary rocks, which are simply the same sand and clay layers cemented together

after burial and consequent subjection to high pressure and temperature.

In seeking to quantify porous medium ﬂow at the large scale, we need to av-

erage the permeability in some way at the mesoscale: larger than the pore scale,

but less than the macroscale. The simplest approach is to suppose that the per-

7.5 Heterogeneous Porous Media 409

meability in a mesoscale block has a random distribution, often assumed to be

a lognormal distribution. An averaged permeability can be derived by supposing,

for example, that ﬂuctuations have small amplitude. One ﬁnds that the consequent

averaged permeability is a tensor, whose components depend on the direction of

ﬂow. In the following section, we consider a more speciﬁc model of the mesoscale

structure, where the heterogeneity is related to the occurrence of fractures in the

medium. This leads to the idea of a secondary porosity associated with the frac-

tures.

7.5.1 Dual Porosity Models

Take a walk on exposed basement rock: at the seaside, in the mountains. Rocks are

not uniform, but are inevitably fractured, or jointed. There are numerous reasons for

this. Sedimentary rocks are lain down over millions of years via the deposition of

outwash clays, sands or calcareous microfossils in marine environments. Over this

time the deposition rate may average a millimetre or less per year. A metre of rock

may take a million, or ten million years, to accumulate. In this time, sea level may

rise or fall by tens or more of metres, and the land itself rises or falls because of

tectonic processes: the crashing of continents, the uplift of mountains, the burial of

sedimentary basins.

It is no surprise that in an exposed sedimentary sequence, such as one sees in

coastal cliffs, rocks form stratigraphic layers separated by unconformities marking

different sedimentary epochs. These unconformities are layers of weakness, and

when the rocks are later subjected to tectonic compression and folding, fractures

will form.

It is not only sedimentary rocks which tear as they are stressed. Igneous rocks

fracture as they solidify because of solidiﬁcation shrinkage. They also form intru-

sions such as dikes and sills, whose different erosional properties can cause subse-

quent voidage.

The occurrence of faulting or jointing in rocks leads to a particular problem in the

description of groundwater ﬂow through them. The rock itself is porous, and admits

a Darcy ﬂow through its pore space; but the fractures act as a second porosity, ad-

mitting a secondary ﬂow which would occur even if the rock itself was completely

impermeable. The situation is illustrated in Fig. 7.8. It is because of this conﬁgura-

tion that the system is called a double, or dual, porosity system, and the resulting

model to describe the ﬂow is called a dual porosity model.

In order to characterise porous ﬂow through such a medium, we distinguish be-

tween the blocks of the matrix and the cross-cutting fractures. We suppose the frac-

tures are tabular, or planar, of width h, and the blocks are of dimension d

, and

that h d

. We denote the blocks by the domain M, and the fractures as ∂M.Be-

cause the fractures are narrow, ∂M essentially represents the external surfaces of

the blocks. We also suppose that d

 l, where l is a relevant macroscopic length