Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

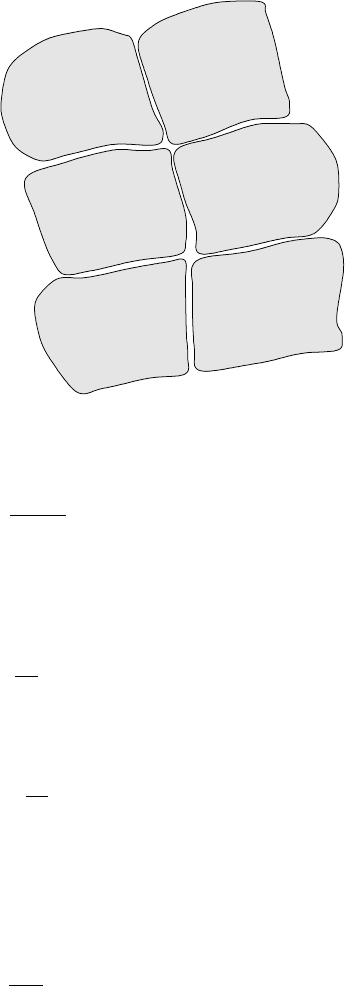
410 7 Groundwater Flow

Fig. 7.8 A doubly porous

system. Porous matrix blocks

are transected by (here) two

sets of transverse fractures

scale. For these tabular cracks, we can deﬁne a fracture porosity

. (7.105)

We deﬁne a matrix pore pressure p

, which is the locally averaged pore pressure

in the matrix blocks, and a fracture pressure p

. There is then a matrix volume ﬂux

per unit area u

, and in the usual way we have Darcy’s law in the form

=−

∇p

, (7.106)

where k

is the permeability of the ﬁne-grained matrix. We have

, (7.107)

where d

is grain size and τ

is a tortuosity factor.

We suppose that ﬂow in the fractures is essentially Poiseuille ﬂow, and this leads

to a prescription of fracture volume ﬂux per unit transverse width of crack, q

(through a single fracture) as

=−

∇p

, (7.108)

where for a plane walled crack of width h, the fracture tortuosity τ

=12; for rough

cracks, one can expect a higher value to be appropriate. The mean fracture velocity

7.5 Heterogeneous Porous Media 411

(which is also the fracture volume ﬂux per unit area of fracture) is thus

=−

∇p

, (7.109)

where we deﬁne the fracture permeability parameter k

. (7.110)

Now if we consider the total (averaged) Darcy ﬂux u through such a doubly porous

medium, it is straightforward to show that

u =(1 −φ

)u



+φ

u



∂M

, (7.111)

where the angle brackets denote averages: for u

, a volume average over the matrix

blocks; for u

, an average over the fractures. Since h  d

, we can effectively

consider the average of u

to be a surface average over the fracture surface denoted

by ∂M, the external boundary of the matrix blocks M. Note that each fracture has

two walls, and thus provides two external surfaces to M.

Our object is to characterise these averages in terms of macroscopic variables,

if possible. Notice that we have already carried out a primary averaging in deﬁning

the ﬂuxes u

and u

in the ﬁrst place: u

is averaged over the grain scale of the

matrix, and u

is averaged over the width of the fractures. However, these ﬂuxes

still represent values at a point within the larger block/fracture system. In particular,

note that by its deﬁnition the fracture ﬂux is parallel to the fracture, and this carries

the implication that

∂p

∂n

=0, (7.112)

where n is the normal to ∂M (and we take it to point from the matrix into the

fracture).

We now want to average over the larger block scale d

. The ‘point’ ﬂuxes u

and u

satisfy the conservation of mass equations

∇.u

=0 (7.113)

and

∇.(hu

) =u

.n|

∂M

, (7.114)

where in (7.114) there is a ﬂux u

.n at the fracture surfaces from the matrix to the

fractures. Some comment on this equation is necessary. It takes this form because

of the fact that the fracture ﬂux as deﬁned in (7.108) is already averaged over the

cross section of the fracture. Continuity of the ﬂuxes at the block fracture interface

produces the source term in (7.114) through the integration of the fracture point

transverse velocity across the fracture.

412 7 Groundwater Flow

To use the ideas of homogenisation, we ﬁrst deﬁne dimensionless variables. We

scale the variables as

∼U, p

∼P, x ∼l, (7.115)

where l is the macroscopic length scale, and we deﬁne a second (now dimensionless)

spatial variable X by putting

x =εX, (7.116)

where

ε =

. (7.117)

The blocks thus have size X ∼ O(1). We write, with an obvious notation, the di-

mensionless gradient operator in the form

∇ =∇

∇

, (7.118)

where we are now using x and X as multiple spatial scales. We suppose that the

block structure is periodic in X, although this is inessential for the methodology.

Now the requirement of (7.112) that

∂p

∂n

=0 implies



∇



=0, (7.119)

whence it follows that we can write, approximately,

=p(x) +ε ˜p

(X), (7.120)

and then

∂p

∂n

≡n.∇

p =−n.∇

˜p

≡−

∂ ˜p

∂N

. (7.121)

p is the macroscopic average pressure variable, and we may impose periodicity in

X of ˜p

with zero mean.

We have continuity of matrix and fracture pressure at ∂M, and therefore we can

write

=p(x) +ε ˜p

(X), (7.122)

and the matrix pressure satisﬁes

∇

˜p

=0inM,

˜p

=˜p

on ∂M.

(7.123)

To ﬁnd the solution ˜p

of (7.123), deﬁne a Green’s function G(X, Y) which satisﬁes

∇

G =δ(X −Y) in M, G =0forY ∈∂M. (7.124)

7.5 Heterogeneous Porous Media 413

Then ˜p

is given by

˜p



∂M

∂G(X, Y)

∂N

˜p

(Y)dS(Y), (7.125)

where

∂

∂N

=n(Y).∇

, and it follows from this that (for X ∈∂M)

∂ ˜p

∂N



∂M

K(X, Y) ˜p

(Y)dS(Y), (7.126)

where

K(X, Y) =

∂

G(X, Y)

∂N

. (7.127)

It remains to determine the fracture pressure perturbation ˜p

. This involves solv-

ing (7.109) and (7.114). Supposing h and k

are constant, these reduce, at leading

order in ε,to

∇

˜p





∂ ˜p

∂N

∂p

∂n



, (7.128)

subject to conditions of periodicity in X and zero mean. Note that the Laplacian in

(7.128) is deﬁned on the surface ∂M.Using(7.126), we can write (7.128)inthe

form

∇

˜p

=α





∂M

K(X, Y) ˜p

(Y)dS(Y) +

∂p

∂n



, (7.129)

where

α =

. (7.130)

The canonical microscale fracture problem to be solved on ∂M is thus

∇

∂M

q =α





∂M

K(X, Y) q(Y)dS(Y) +n



, (7.131)

with periodic boundary conditions and zero mean, and then

˜p

=q(X).∇

p. (7.132)

We now use these results to ﬁnd the effective permeability of the medium. Aver-

aging (7.106) over the matrix blocks yields (dimensionlessly)

Uu



=−

μl

∇

p, (7.133)

since ˜p

is continuous across fractures and periodic in X. In a similar way,

Uu



∂M

=−

μl



∇

p +∇

˜p



∂M



, (7.134)

414 7 Groundwater Flow

but the surface average term in this expression does not obviously vanish. We have

∇

˜p



∇

˜p

−n(n.∇

˜p

)



+n(n.∇

˜p

); (7.135)

the term in square brackets is a tangential derivative of ˜p

along ∂M, and we sep-

arate the terms in this way because ˜p

is only deﬁned on ∂M. In addition, because

˜p

=˜p

on ∂M, we could replace the subscript f by m in the square-bracketed

expression. Because of (7.121), we have

n(n.∇

˜p

) =−n(n.∇

p), (7.136)

and thus



n(n.∇

˜p

)



∂M

=−e

n



∂M

∂p

∂x

, (7.137)

where e

is the unit vector in the x

direction. We therefore have

Uu



∂M

=−

μl



I −nn

∂M



.∇

p +



∇

˜p

−n(n.∇

˜p

)



∂M



, (7.138)

where I is the unit tensor, and nn is the tensor with elements n

We now substitute the expression for ˜p

in (7.131)into(7.138); averaging over

∂M, we ﬁnally derive the expression for the mean fracture velocity in the dimen-

sionless form

Uu



∂M

=−

μl



I −nn

∂M





(I −nn).∇





.∇

p. (7.139)

Rewriting this in dimensional form, we have

u



∂M

=−

∗

.∇p, (7.140)

where the fracture relative permeability tensor k

∗

is deﬁned by

∗



(δ

−n

)



∂q

∂X



∂M

. (7.141)

Equally, the dimensional matrix ﬂux is, from (7.133),

u



=−

∇p. (7.142)

(7.140), (7.141) and (7.142) give the recipes for the averaged matrix and fracture

ﬂuxes in terms of the macroscopic pressure gradient and the solution of the block

scale fracture pressure problem (7.131).

If we take a representative volume consisting of many blocks, and integrate

(7.113) over the matrix volume, and (7.114) over the fracture volume, we obtain

7.6 Contaminant Transport 415

the averaged (dimensional) equations for the averaged ﬂuxes in the form

∇.



u



∂M



u

.n

∂M

∇.



(1 −φ

)u





=−s

u

.n

∂M

(7.143)

where s

is the speciﬁc fracture surface area (i.e., surface area per unit volume: here

∼d

−1

). Note that the source term in (7.143)isjust

u

.n

∂M

=−

μl



∂ ˜p

∂N



∂M

, (7.144)

because 

∂p

∂n



∂M

=n

∂M

.∇

p =0,

and in the present case this is just zero because

of (7.123).

The usefulness of all this methodology is that it carries across to other, more

complicated averaging problems (as we see below), but in the present case of in-

compressible double porosity ﬂow, it may be somewhat unnecessary. The reason

for this is that fracture relative permeability depends on the solution of (7.131), and

thus on the fracture geometry and the single dimensionless parameter α given by

(7.130). Assuming small fracture porosity, the ratio of matrix ﬂow to fracture ﬂow

is, from (7.111), (7.109), (7.105) and (7.106), of the order of

φu

∼

=α. (7.145)

If α is large, then very little ﬂow occurs through the fractures anyway, and the sec-

ondary porosity is of little concern. If α is small, the blocks are essentially imper-

meable, and the fracture network is crucial; but then the solution of (7.131)isjust

q =O(α), and the relative permeability is simply

∗

=I −nn

∂M

, (7.146)

which only differs from the unit tensor if the medium is anisotropic. It is only in the

case α =O(1) that the competition between the two systems becomes important. If

we use values τ

=10

, d

=1m,h =10

−3

m and k

=10

−12

(cf. Table 7.1),

we get α ≈0.01. This might be appropriate for a fractured sandstone on a regional

scale. Generally, the primary and secondary (fracture) permeability will only be

comparable if the host rock is itself quite permeable.

7.6 Contaminant Transport

Much of the interest in modelling groundwater ﬂow lies in the prediction of solute

transport, in particular in understanding how pollutants will disperse: for example,

The average of n over ∂M is zero because the normals on opposite sides of a fracture are in

opposite directions. More speciﬁcally,



∂M

φn dS =



∇φdV, thus



∂M

ndS =0.

416 7 Groundwater Flow

how do nitrates used for agricultural purposes disperse via the local groundwater

system? Mostly simply, one would simply add a diffusion term to the advection of

the solute concentration c:

φc

+u.∇c =∇.[φD∇c]. (7.147)

The diffusive width l of a sharp front travelling at speed u after it has trav-

elled a distance l is of the order of l ∼(Dl/u)

1/2

;ifwetakeD ∼ 10

−9

−1

u ∼ 10

−6

−1

(30 m y

−1

), l = 10

m, then l ∼ 1 m, and the diffusion zone is

relatively narrow. For a more porous sand, the diffusion width is even smaller.

In fact, as velocity increases, the effect of diffusion increases. That this is so is

due to a remarkable phenomenon called Taylor dispersion, described by G.I. Taylor

in 1953. Consider the diffusion of a solute in a tube of circular cross section through

which a Poiseuille ﬂow passes. If the mean velocity is U and the tube is of radius a,

then the velocity is 2U(1 −r

), and the concentration satisﬁes the equation

+2U



1 −r







, (7.148)

where x is measured along the tube, and r is the radial coordinate. Taylor showed,

rather ingenuously, that when the Péclet number Pe =aU/D is large, then the effect

of the diffusion term in (7.148)istodisperse the mean solute concentration diffu-

sively about the position of its centre of mass, x =Ut, with a dispersion coefﬁcient

of a

/48D. Aris later improved this to

48D

+D, (7.149)

which is asymptotically valid for x  a. The dispersive mechanism is due to the

radial variation of the velocity proﬁle, which can disperse the solute even if the

diffusion coefﬁcient is very small.

Typically, this is generalised for porous media (where we think of the pores as

being like Taylor’s tube) by writing the dispersion coefﬁcient as

∗



, (7.150)

where D

∗

represents molecular diffusion and D



dispersion in the direction of ﬂow.

The tortuosity of the ﬂow paths and the possibility of adsorption on to the solid

causes D

∗

to be less than D, and ratios D

∗

/D between 0.01 and 0.5 are commonly

observed. In porous media, remixing at pore junctions causes the dependence of D



on the ﬂow velocity to be less than quadratic, and a relation of the form



=αu

, (7.151)

where u is the Darcy ﬂux, ﬁts experimental data reasonably well for values 1 <

m<1.2. A common assumption is to take m = 1. Mixing at junctions also causes

transverse dispersion to occur, with a coefﬁcient D

⊥

which is measured to be less

than D



by a factor of order 10

when Pe  1. Dispersion is thus a tensor property.

7.6 Contaminant Transport 417

If we write



=α



|u| (7.152)

for the longitudinal dispersion coefﬁcient, and

⊥

=α

⊥

|u| (7.153)

for the lateral dispersion coefﬁcient, then a suitable tensor generalisation is

=α

⊥

|u|δ

+(α



−α

⊥

)

|u|

, (7.154)

where δ

is the Kronecker delta.

The conservation of solute equation is then

∂c

∂t

+u.∇c =∇.



φD

.∇c



∂

∂x



φD

∂c

∂x



. (7.155)

For a one-dimensional ﬂow in the x direction, c satisﬁes

∂c

∂t

∂c

∂x

∂

∂x





∂c

∂x



∂

∂y



⊥

∂c

∂y



∂

∂z



⊥

∂c

∂z



(7.156)

(v =u/φ is the linear velocity) and if the dispersivities are constant, then the solu-

tion for release of a mass M at the origin at t =0is

c =

8φ(πD



)

1/2

⊥

3/2

exp



−

(x −vt)



−

⊥



, (7.157)

where r

7.6.1 Reactive Dual Porosity Models

Let us now consider the reactive transport of a contaminant of concentration c within

a fractured soil or rock which has dual porosity. We follow the ideas of averaging

and homogenisation in Sect. 7.5.1. The point forms of the equations are taken in the

form

∂c

∂t

+∇.(cu) =∇.[D∇c]+S

∂c

∂t

+∇.(c

u) =∇.[D

.∇c

]+S

(7.158)

where S

, S

represent source or sink terms due to chemical reaction, D is the

molecular diffusion coefﬁcient of the contaminant within the fractures, and D

418 7 Groundwater Flow

the dispersivity within the matrix blocks. The concentrations within the fractures

and matrix are denoted by c and c

, respectively.

The ﬁrst thing to do is to average the fracture concentration equation across the

width of the fracture. When we do this, we effectively regain the Taylor dispersion

equation, with the addition of the reaction terms, and also a solute ﬂux delivered

from the matrix:

∂c

∂t

+∇.(c

) =∇.[D

.∇c

]+S

−



(n.D

.∇c

) −c





∂M

. (7.159)

This equation is analogous to (7.114). It differs from (7.158) in that c

is the cross-

sectional average concentration (actually, in the derivation of the Taylor dispersion

equation, one ﬁnds the concentration is cross-sectionally uniform, so that c

= c);

is the cross-sectionally averaged fracture velocity, just as before; and D

is the

local dispersion coefﬁcient: it will be modiﬁed again at the larger macroscale. The

reaction term S

depends on cross-sectionally averaged concentrations, which equal

their point forms, so that S

is unchanged.

Now we write down the equivalents of (7.143). We deﬁne the block averaged

concentrations

¯c

=c

|

, ¯c

=c

|

∂M

, (7.160)

where as before c|

denotes an average of c over the matrix blocks M, and c|

∂M

denotes the average of c over the fracture surface ∂M. Then we have the equation

for ¯c

∂

∂t

(φ

¯c

) +∇.[φ

¯c

]=∇.[φ

.∇¯c

]+φ



n.{c

−D

.∇c

}





∂M

. (7.161)

We can make use of (7.143)

, and the fact that c

on ∂M, to simplify this to



∂ ¯c

∂t

.∇¯c



=∇.[φ

.∇¯c

]+φ

−s

n.D

.∇c

|

∂M

. (7.162)

The speciﬁc fracture surface area is deﬁned as s

, as before. The macroscopic frac-

ture dispersivity D

here is distinct from D

, in the same way that Taylor dispersion

in a tube is distinct from that in a porous medium; in this case it is because of remix-

ing of fracture ﬂuid at the junctions between fractures at the block boundaries. The

formal averaging assumption which is made is

D

.∇c

−c

|

∂M

.∇¯c

−¯c

u

|

∂M

, (7.163)

and this has some justiﬁcation insofar as it is just this result which emerges in the

study of Taylor dispersion.

7.6 Contaminant Transport 419

In a similar way to the derivation of the average fracture concentration equation,

the matrix averaged concentration satisﬁes

(1 −φ

)



∂ ¯c

∂t

.∇¯c



=∇.



(1 −φ

.∇¯c



+(1 −φ

)

n.D

.∇c

|

∂M

. (7.164)

The result of averaging is the two Eqs. (7.162) and (7.164) for the average

fracture and matrix concentrations. In principle, the block average fracture dis-

persivity D

should be calculable by solving the local block problem, although

in practice one would assume a value by analogy with assumptions about porous

medium dispersion coefﬁcients. However, unlike the incompressible dual porosity

mass ﬂow equations (7.143), the source term s

n.D

.∇c

|

∂M

is non-zero, and

this must be constituted, ideally by solving the block scale problem, which is given

by Eqs. (7.158)

and (7.159); these can be slightly simpliﬁed to the forms

∂c

∂t

.∇c

=∇.[D

.∇c

]+S

∂c

∂t

.∇c

=∇.[D

.∇c

]+S

−

(n.D

.∇c

∂M

(7.165)

The boundary condition for c

is that

on ∂M, (7.166)

and c

is periodic over ∂M.

The basis for the method of homogenisation is the expansion of the local block

problem in terms of the parameter ε = d

/l, where d

is the block scale and l is

the macroscopic length scale. However, because of the complexity of the equations

to be solved, the application of this method must be done judiciously.

To illustrate this point, suppose that the dispersion coefﬁcient tensors are all

isotropic, and equal to D

I, where D

is constant, and that suitable (macroscopic)

scales for the variables are c ∼c

, x ∼l, u ∼U, t ∼l/U, and suppose to be precise

that the reaction kinetics are ﬁrst order, i.e., S =−rc, and that the speciﬁc frac-

ture surface area is constant, s

=1/d

. The dimensionless equation for the matrix

average ¯c

is then

(1 −φ

)Pe



∂ ¯c

∂t

.∇

¯c



=(1 −φ

)∇

¯c

−PeΛ(1 −φ

)¯c



∂c

∂N





∂M

, (7.167)

where

∂c

∂N

denotes n.∇

, and

Pe =

,Λ=

. (7.168)