Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

420 7 Groundwater Flow

The local block equation (7.165)

rewritten in the block variables

X =

,T=

, (7.169)

is then

εPe



∂c

∂T

.∇



=∇

−ε

PeΛc

. (7.170)

What is obvious is that all the terms cannot balance in both local and global prob-

lems, and this leads to simpliﬁcations. The simplest case is where the macroscopic

Péclet number and reaction number Λ are both taken to be O(1); then (7.167) sug-

gests that in (7.170) we put

=¯c(x) +ε

˜c

(X) (7.171)

(and thus also c

=¯c(x) +ε

˜c

(X)); both inner and outer problems are well scaled,

and the advective term can be neglected in solving the inner problem, which in fact

reduces approximately to Poisson’s equation. Speciﬁcally, using multiple scales in

both x and t, we have at leading order in ε,

∇

˜c

=Pe



∂ ¯c

∂t

.∇

¯c



+PeΛ ¯c −∇

¯c (7.172)

subject to ˜c

=˜c

on ∂M and conditions of periodicity on M. (If we integrate

(7.172) over M, we regain the averaged equation (7.164) as an integrability condi-

tion for (7.172), as expected via homogenisation.)

In a similar way, the leading order local equation for the fracture perturbed con-

centration ˜c

∇

˜c

−

(1 −φ

)

∂ ˜c

∂N



∂M

=Pe



∂ ¯c

∂t

.∇

¯c



+PeΛ ¯c −∇

¯c (7.173)

(note that a term

(1−φ

)

εφ

∂ ¯c

∂n

∂M

∝∇

¯c.n|

∂M

is identically zero, because the normals

n on the two faces of a fracture cancel each other). ˜c

satisfying (7.173) is subject to

periodicity in ∂M and zero mean. As for the ﬂuid ﬂow, we can solve (7.172)using

a Green’s function for the Laplacian in M, so that the boundary derivative term

in (7.173) becomes an integral convolution in terms of ˜c

. We then solve (7.173)

using a Green’s function for the Laplacian on ∂M. This allows us to determine the

homogenised equation for ¯c (see Question 7.13).

In fact, it is rarely the case that Pe and Λ are O(1): more commonly they are both

large. Suppose for example that ε = 10

−4

, Pe = 10

, Λ = 10

: not unreasonable

values (as we shall see below). Putting

p =εPe,λ=εΛ, (7.174)

7.7 Environmental Remediation 421

it seems natural to take λ ∼ p ∼O(1). The block problem becomes (in terms of T

and X only)



∂c

∂T

.∇



=∇

−λp c

, (7.175)

which implies that reaction occurs on the block scale. This is a linear equation for c

which can in principle be solved to give the boundary ﬂux term in the c

equation

as a convolution integral in terms of c

. In a strict sense, this distinguished limit

describes the structure of a reaction front in which both reaction and dispersion are

important. Outside this front, reaction and dispersion are negligible, and the reactant

simply advects with the ﬂow.

Importantly, it implies that the speed of the front is

determined by the local diffusion and reaction within the block.

If Λ is even larger than this, so that λ 1, then the reaction is fast at the block

scale, and occurs in a thin rind within the block; for a single species, as here, this

rind must be on the boundary, as the interior reactant concentration reaches zero

rapidly. Bearing in mind that the normal coordinate n at ∂M points into the fracture,

the boundary layer solution for c

is just

≈c

exp



(λp)

1/2



, (7.176)

and thus the ﬂux term in the local fracture equation derived from (7.165)

−

∂c

∂n



∂M

=−

(λp)

1/2

. (7.177)

Hence c

satisﬁes the local equation

∇

−

(λp)

1/2



∂c

∂T

.∇



+λp c

. (7.178)

As is perhaps obvious, the reaction is fast in the fractures also and c

rapidly ap-

proaches zero.

7.7 Environmental Remediation

Environmental pollution is now an endemic phenomenon. All over every industri-

alised country, spills of hydrocarbons, efﬂuents, and industrial waste have caused

pollution of underlying groundwater. The resulting ‘plumes’ move slowly with the

prevailing background groundwater ﬂow, and in course of time will enter streams,

rivers and lakes, with consequent health risk via the contamination of drinking wa-

ter. Short of more drastic measures such as pumping out polluted groundwater and

Actually, this only makes sense for multi-species reactions of the form A +B →P ,forthenthe

reaction rate ∝AB, and can be zero by virtue of A = 0 on one side of the front, and B =0onthe

other.

422 7 Groundwater Flow

treating it, natural bioremediation anticipates that microbial action will eventually

break down most pollutants, rendering them harmless. The issue for the environ-

mental scientist is to predict the future movement of the plume, and the likelihood

of microbial breakdown before it reaches drinking water sources.

In so doing, groundwater ﬂow modelling is essential, because of its ability to

predict into the future, and also because accurate monitoring of subsurface contam-

ination is expensive and not straightforward. Against this, subsurface soil and rock

is usually an extremely heterogeneous medium, both physically and chemically, and

the validation of computational results is difﬁcult.

7.7.1 Reactive Groundwater Flow

The general context of many subsurface pollution problems of concern is similar,

and we therefore begin with some generalities. Contaminants may be aqueous, in

which case they mix with the groundwater, or non-aqueous, in which case they

do not. Hydrocarbons, for example, are non-aqueous. Amongst the non-aqueous

phase liquids (NAPLs), one distinguishes dense liquids (DNAPLs) from light ones

(LNAPLs). DNAPLs will sink into the saturated zone, whereas LNAPLs, such as

hydrocarbons, will sink to the base of the unsaturated zone, and there sit on the

water table, from where their constituents may diffuse downwards.

The contaminant plume will typically consist of a cocktail of different chemicals,

which ﬂow with the local groundwater ﬂow, disperse within it, and react with oxy-

gen and other substances in the soil via the agency of microbial action. The typical

sort of model of concern is thus the reaction-advection-dispersion equation

∂c

∂t

+∇.(cu) =∇.(D .∇c) +S, (7.179)

where c is one of a sequence of reactants, u is the local groundwater ﬂux (given by

Darcy’s law), D represents dispersion, and is typically anisotropic, in the sense that

dispersion in the longitudinal direction is larger than lateral dispersion. Dispersion

itself is partly due to molecular diffusion, but more importantly (at high grain scale

Péclet number) is due to grain scale shear-induced distortion of the ﬂuid associated

with Taylor dispersion, together with remixing at pore junctions. Typically, the lon-

gitudinal dispersion coefﬁcient D



∼ d

|u|, where d

is grain size, while lateral

dispersion D

⊥

is a factor of 10–100 smaller.

The coefﬁcient R is the retardation factor, and it is a slowing rate due to the ad-

sorption of aqueous phase concentration on solid particles. Speciﬁcally, we actually

have two separate conservation laws for solid and aqueous concentrations c

and c

respectively, thus

∂c

∂t

+∇.(c

u) =∇.(D.∇c

) +S +k

−k

∂c

∂t

=−k

(7.180)

7.7 Environmental Remediation 423

where k

and k

are desorption and adsorption rates, respectively. (7.180) speciﬁ-

cally assumes that the reaction occurs only in the aqueous phase, by way of example.

Now the point is that if the sorption rates are very large (and constant), then the

second equation in (7.180) tells us that

≈

, (7.181)

and the sum of the two equations then gives us (7.179), with the retardation factor

R =1 +

. (7.182)

The source term S represents reaction driven sources and sinks. It is typically

the case that there are many, many reactions and reactants. Equally typically, many

of the reaction rates are not well known, and the rates may be widely disparate. In

general this will imply that many reactions can be taken to be in equilibrium, with

only the slowest (rate-controlling) reaction being of dynamical importance.

7.7.2 Biomass Modelling

The reaction terms S in (7.180) are mediated by bacteria within soil, which consume

the various nutrients provided through metabolic reactions. Like all living things,

microbes survive by generating energy from nutrients through a variety of such re-

actions. This process involves a network of redox (oxidation–reduction) reactions,

and involves the overall exchange of electrons between two distinct chemical fuels

which are consumed in the reactions; the metabolic process is in this case called

respiration. While there may be a number of such fuels, there is a hierarchy in their

use. Dissolved oxygen is commonly the terminal electron acceptor (as the exter-

nally sourced oxidant is typically referred to), while an organic carbon compound

is the electron donor. When these preferred substrates are absent or depleted, other

compounds can be used instead. When the same organic compound is used as both

donor and acceptor, the metabolic process is called fermentation.

Many bacteria are able to use several reaction pathways independently, giving

them a degree of ﬂexibility to differing conditions. This capability is very species-

dependent, and competition ensures that the species which are best adapted to

local conditions become dominant. Microbial growth depends heavily on energy

metabolism but also requires the uptake of other substrates needed to generate new

biomass. Growth rate is generally limited by the supply of one or more substrates,

but saturates to a maximum growth rate in conditions of ample supply. The depen-

dence of bacterial growth rate is commonly taken, by analogy with simple enzyme

kinetic uptake rates, as proportional to

K+c

, where c is the relevant nutrient con-

centration, and K is a constant; such kinetics are called Monod kinetics. When two

424 7 Groundwater Flow

nutrients control growth, as in respiration, it is usual to take the growth rate as pro-

portional to the product of two Monod factors, thus (for example)

S =−r

, (7.183)

in which r

is a reaction rate constant, and X is the biomass density.

More complex models also consider the growth of the microbial population X

in terms of the nutrient supply, in particular in the form of a microbial mat which

becomes attached to the soil grains, and usually called a bioﬁlm. In particular, the

concept of biodegradation, for example of oil spills in sea water, or of factory efﬂu-

ent in groundwater, commonly involves the development of bacterial colonies which

are able to efﬁciently use the offending contaminant to promote their own growth.

7.7.3 Non-dimensionalisation

It is commonly the case that the water table is at a depth of 10–20 metres, whereas a

plume may have spread (or we are concerned with whether it will spread) a distance

of order kilometres. Therefore these plumes generally have high aspect ratio, a cause

both of computational stress and analytical simpliﬁcation. The latter may be offset

by the decreased lateral dispersion coefﬁcient, as we now show.

Let us consider the scalar contaminant equation (7.179) in two dimensions, with

horizontal and vertical coordinates x and z, corresponding Darcy ﬂuxes u and w,

and longitudinal (horizontal) and transverse (vertical) dispersivities D



and D

⊥

which we take to be constant. We suppose l and d are suitable horizontal and vertical

length scales, U is a horizontal Darcy ﬂux scale (and therefore mass conservation

implies that hU/ l is a suitable vertical ﬂux scale), Rl/U is then the convective time

scale, and we take S

to be a measure of the reaction rate term, and c

to be a typical

contaminant concentration. The units of concentration are mol l

−1

(moles per litre),

and the units of S

are mol l

−1

We deﬁne dimensionless variables by writing

u =Uu

∗

,w=

∗

,c=c

∗

,t=

∗

x =lx

∗

,z=dz

∗

, S =S

(7.184)

substituting these into (7.179) (and forthwith dropping the asterisks), we obtain the

dimensionless equation

∂c

∂t

∂c

∂x

∂c

∂z



∂

∂x

⊥

∂

∂z

+ΛS, (7.185)

where



, Pe

⊥

,Λ=

. (7.186)

7.8 Three Speciﬁc Remediation Problems 425

The aspect ratio d/l and transverse dispersivity ratio D

⊥



compete against

each other, and generally we might suppose Pe

⊥

∼Pe



; but also if D



∼d

U , then

we can expect that usually Pe



1, heralding the existence of thin boundary layers

in which dispersion is effective. The parameter Λ is the ratio of advection time

to reaction time, and will often be very large for microbially mediated reactions

of interest. These two observations cause numerical difﬁculties in solving (7.186),

but can aid analytical insight. In the following section, we discuss three speciﬁc

groundwater contamination problems of recent concern.

7.8 Three Speciﬁc Remediation Problems

Four Ashes Four Ashes is a site in the Midlands of England where a ﬁfty year

old plume of phenol (C

0) and other contaminants, about 500 metres long, lies

within the saturated zone. The plume is thought to lie between depths of 10 m and

30 m at 130 m from the source, but is sinking as it moves west (perhaps because

of surface recharge), reaching depths 21–44 m at 350 m distance (this information

comes from two boreholes drilled at the site). Degradation is very slow: perhaps

only 5% of the total contaminant load has so far been degraded. This is thought

to be due to toxicity of the phenol within the plume, and to supply limitation of

electron acceptors (oxygen and nitrate) at the plume fringe.

The overall reaction scheme which is considered to apply is that the phenol is

oxidised at the plume boundary by oxygenated groundwater, producing TIC (to-

tal inorganic carbon). Within the plume, phenol is fermented to produce hydrogen

amongst other things, which then reduces various oxides within the soil via mi-

crobial agency. A suitable set of reactions to describe the situation consists of the

following:

O +7O

+3H

→6HCO

−

+6H

O +5.6NO

−

+0.2H

→6HCO

−

+0.4H

+2.8N

O +5H

→3CH

COOH +2H

O +17H

→6HCO

−

+6H

+14H

+MnO

2(s)

+2H

→2H

O +Mn

+2FeOOH

(s)

+4H

→4H

O +2Fe

+SO

2−

+0.25H

→H

O +0.25HS

−

+CO

2−

+0.5H

→0.75H

O +0.25CH

(7.187)

and r

–r

are the reaction rates, deﬁned using Monod kinetics. In terms of the reac-

tion rates, the source term in each reactant equation is then



, (7.188)

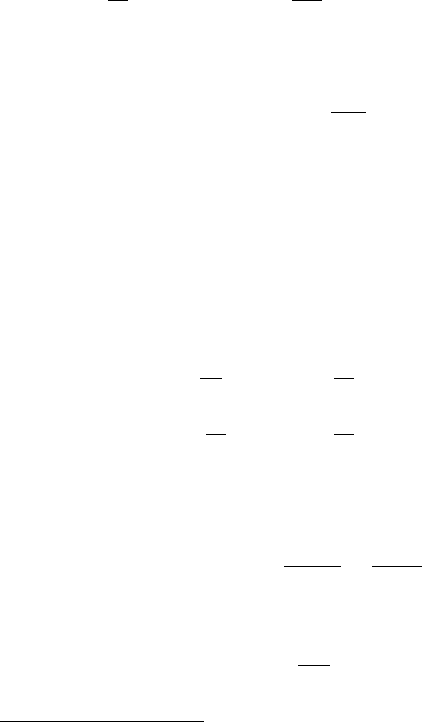
426 7 Groundwater Flow

where s

is the (sign dependent) stoichiometric coefﬁcient for reactant j in reac-

tion l.

The maximum (saturated) rates k

of the Monod rates r

are thought to range

from about 10

−13

mol l

−1

to about 10

−10

mol l

−1

. The background phenol

concentration p

is of the order of 10

−10

mol l

−1

, and the aqueous dissolved oxygen

level c

is of order 10

−4

mol l

−1

. The horizontal Darcy ﬂux is estimated to be U =

10 m y

−1

. The dispersivities are taken in the form D =αU, and values of α



=1m

and α

⊥

=4 ×10

−4

m are assumed.

Also, we take l =500 m, d =20 m, and R =1.

With all of these values, we have



=500, Pe

⊥

=2000,Λ∼10

–10

, (7.189)

where the deﬁnition of Λ is based on p

, i.e.,

Λ =

. (7.190)

As suggested, Pe



∼Pe

⊥

1, and the reaction rate parameter Λ is extremely large.

To get an idea of the solution behaviour when Pe 1 and Λ  1, we consider the

simpler reaction

O +σ O

→products, (7.191)

where σ is a suitable stoichiometric coefﬁcient. The corresponding version of

(7.185)issimply

∂p

∂t

+∇.(pu) =

∇

p +ΛS,

∂c

∂t

+∇.(cu) =

∇

c +νΛS,

(7.192)

where p and c are the concentrations of the two species (phenol and oxygen), and

the reaction term is just

S =−







; (7.193)

the parameter ν is given by

ν =

σp

∼10

−6

. (7.194)

For both theoretical and experimental reasons, we expect α



∼ d

, the pore or grain size (Bear

1972, p. 609), with α

⊥

/α



∼0.01–0.05 (Sahimi 1995, p. 225). The large value of α



here suggests

ﬂow in sub-parallel fractures with spacing on the order of a metre.

We can take Pe



=Pe

⊥

by choosing d appropriately.

7.8 Three Speciﬁc Remediation Problems 427

The asymptotic structure of the solution of (7.192) is easily given. For Λ 1, the

reaction region is very thin, and will occur only at the fringe of the plume. Outside

the plume, p = 0, while inside the plume c = 0, so that S = 0 everywhere apart

from the reaction front, which is located at the plume boundary. Denoting the plume

by P and its boundary by ∂P, we thus have to solve

∂p

∂t

+∇.(pu) =

∇

p, x ∈P,

∂c

∂t

+∇.(cu) =

∇

c, x /∈P,

(7.195)

and p and c both satisfy p =c =0on∂P. The location of P has to be determined

(it is a free boundary), but this is simply done because of the precise conservation

law for c −νp, which follows from (7.192):

∂(c −νp)

∂t

+∇.



(c −νp)u



∇

(c −νp). (7.196)

Integrating this across the reaction front yields the extra condition

to determine

the front ∂P:

∂c

∂n

=ν

∂p

∂n

. (7.197)

Note that the normal derivative here has to be treated with some attention when

non-dimensionalised. If the plume fringe is at dimensionless position z = ζ(x,t),

then the dimensional normal component of the dispersive ﬂux of oxygen (in terms

of dimensionless variables) is just

(D.∇c).n =

l(1 +δ

)

1/2



⊥

∂c

∂z

−



∂c

∂x

∂ζ

∂x



, (7.198)

where δ is the aspect ratio. There is a similar expression for ∂p/∂n. It follows from

this that more generally, the conservation boundary condition (7.197) can be ex-

pressed as

⊥

∂c

∂z

−



∂c

∂x

∂ζ

∂x

=ν



⊥

∂p

∂z

−



∂p

∂x

∂ζ

∂x



, (7.199)

and to interpret this as (7.197) requires the unit normal n to be suitably deﬁned.

The problem is even easier when (as here) Pe 1. Then diffusive boundary lay-

ers of (dimensionless) thickness O(1/Pe

1/2

) adjoin the plume boundary, and away

from these, the reactants are simply advected with the ﬂow.

In the present case, the parameter ν 1. This modiﬁes the discussion as follows.

Reaction must still occur in thin regions, outside which the reactants obey (7.195),

In this particular case, it is even simpler, since we just integrate the convective-diffusion equa-

tion (7.196) with appropriate external boundary conditions, and ∂P is located by the curve where

c −νp =0.

428 7 Groundwater Flow

but there cannot be a front (in the sense of a moving boundary) at which c =

∂c

∂n

=0.

If, for example, we have the one-dimensional problem

+uc

, (7.200)

with c = 1att =0 and as x →∞, and c =0atx =0, then if Pe ∼O(1), reaction

occurs near x =0, oxygen supply being sufﬁcient to remove the phenol. If Pe  1,

then a front moves away from x =0 at speed u. Behind this front, c ≈ 1, ahead of

it c ≈ 0, and the front itself is purely diffusional, of width O{(t/Pe)

1/2

},havingan

error function proﬁle for solution.

Rexco The site was a former coal carbonisation plant (between 1935 and 1970)

where ammonium liquor had been allowed to drain on site. The liquid drained

through the unsaturated zone of some 18 metres depth to the saturated zone, where

it is spreading as a plume of some 25 metres depth in a sandstone aquifer. At the

plume fringe, ammonium ions (NH

) ions are subject to oxidation, releasing nitro-

gen. Phenol is also present in front of the ammonium, which is highly retarded (with

a retardation factor of R = 5). Well extraction by a new factory on site is causing

the groundwater ﬂow ﬁeld to be time dependent, and this is an issue in modelling

studies.

The modelling scheme is similar to the Four Ashes site, but less is known of the

reaction rates. The reactions which are considered to be important for the ammo-

nium are

+2O

→ NO

−

O +2H

−

+1.25CH

O +H

→ 0.5N

+1.25CO

+1.75H

O, (7.201)

+0.6NO

−

→ 0.8N

+1.8H

O +0.4H

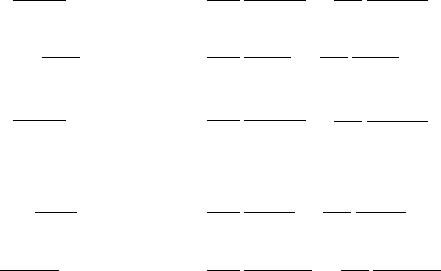
The kinetics (only) of these reactions is described by the ﬁve ordinary differ-

ential equations for the ﬁve reactants, ammonium NH

, oxygen O

, nitrate NO

−

hydrogen ion H

and organic carbon CH

=−r

−r

=−2r

−

−r

−0.6r

=2r

−r

+0.4r

=−1.25r

(7.202)

7.8 Three Speciﬁc Remediation Problems 429

To estimate Péclet numbers, we take d = 25 m, l = 1000 m, R = 5, U =

100 m y

−1

. Values of dispersion coefﬁcients are uncertain, so we choose for il-

lustration D



= 100 m

−1

, D

⊥

= 10 m

−1

, i.e., α



= 1 m (like Four Ashes)

and α

⊥

=0.1 m. The (unretarded) time scale l/U is then 10 years, and Pe



∼10

⊥

∼6. These values are not too reliable, and perhaps are consistent with a highly

fractured aquifer. For a homogeneous medium, we would expect much smaller α,

and thus much larger Pe.

It is possible to extend the Four Ashes discussion of the simple phenol/oxygen

reaction to the more complicated scheme above. Reaction rates are not well known.

Most of the reactants are present at the level of mmol l

−1

(millimole per litre). Spe-

ciﬁc estimates are

∼12 mmol l

−1

∼0.3 mmol l

−1

−

∼0.15 mmol l

−1

∼10

−4

mmol l

−1

∼1 mmol l

−1

(7.203)

If we use ˆc

= 12 mmol l

−1

as a concentration scale in the deﬁnition of Λ in

(7.186) and arbitrarily pick a reaction rate scale of S

= 10

−10

mol l

−1

(com-

parable to phenol degradation rate at Four Ashes), then we have Λ ∼O(1), and the

simple description for Four Ashes is inappropriate.

Despite this, it is thought that reactions are fast, and we will suppose that in fact

Λ  1. In particular, there are data from a borehole measurement which appear

to be consistent with the idea that there is a thin reaction zone at the upper plume

boundary. Oxygen (presumably) diffuses to this front from above, and ammonium

from below; in the reaction zone there is a huge spike of nitrate (see Fig. 7.9). We

wish to see whether the existence of this nitrate spike is consistent with the model,

assuming the measurement was realistic. (Figure 7.9 actually suggests the existence

of two fronts, with nitrate produced at the upper front diffusing down to the second

front, but we will focus only on the upper front.)

The dimensionless equations equivalent to (7.192) for the reaction scheme

(7.201)are

∂c

∂t

+∇.(c

u) =

⊥

∂

∂z



∂

∂x

−Λ(r

∂c

∂t

+∇.(c

u) =

⊥

∂

∂z



∂

∂x

−2Λν

∂c

−

∂t

+∇.(c

−

u) =

⊥

∂

−

∂z



∂

−

∂x

+Λν

−

−r

−0.6r

∂c

∂t

+∇.(c

u) =

⊥

∂

∂z



∂

∂x

+Λν

(2r

−r

+0.4r

∂c

∂t

+∇.(c

u) =

⊥

∂

∂z



∂

∂x

−1.25Λν

(7.204)