Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

460 7 Groundwater Flow

Show that, if we deﬁne c

∗

to be the solution of

∇

∗

=1inM,

with

∗

=0on∂M,

then



∂M

∂G(X, Y)

∂N

(Y)dS(Y) +R

∗

and deduce that, for X ∈M,

∇

−(1 −φ

)



∂M

K(X, Y)c

(Y)dS(Y)

=φ

+(1 −φ

∂c

∗

∂N



∂M

By integrating this equation over ∂M, show that the condition of periodicity

of c

implies that the equation to determine ¯c is



∂ ¯c

∂t

+u.∇

¯c



=∇

¯c −PeΛ ¯c,

where u =φ

+(1 −φ

7.16 The reaction rates in the reactions

−→ X

+nH

KFs

−→ K

+AlO

−L

+s SiO

+AlO

−L

+f X

−→ f I

+SiO

SiO



−

Qz,

are related by

≈ fr

≈ r

−r

−

≈ (s +1)r

The reaction rate r

is given by

=φ



1 −



1 −



−1 −

(s+1)r





7.13 Exercises 461

where φ

are porosities, R

are rate factors (such that r

∝ R

), and the stoi-

chiometric constants f and s, and the constant θ

, may be taken as O(1) (and

> 1). Show that r

can be written explicitly in the form



(θ

−1)γ

s +1

(θ

−1)γ





(θ

−1)γ

s +1

(θ

−1)γ



4(s +1)

(θ

−1)γ





1/2

where the coefﬁcients γ

represent the porosity weighted rate factors, i.e.,

=φ

,γ

=φ

,γ

=φ

,γ

=φ

Deduce that the slowest reaction of the four (as measured by γ

) controls the

overall rate, and give explicit approximations for r

for each of the consequent

four possibilities.

Chapter 8

Mantle Convection

It is now virtually common knowledge, extending into the school curriculum, that

the Earth’s surface is constructed of a number of ‘plates’, and the grinding of these

against each other is the principal cause of much of the Earth’s volcanism, its earth-

quakes, and is also the geometric cause of mid-ocean rises and oceanic trenches.

Scientiﬁc television programmes abound with the story of how Iceland lies at the

boundary of two of these plates, how it is being formed by their creation, or how

the Hawaiian Islands are being created by volcanism beneath the overriding Paciﬁc

plate.

The thrusting of one plate into another tells us why the Alps or Himalayas have

been formed; the sinking of plates in subduction zones is what causes oceanic

trenches to occur, and the frictional rubbing of the subducting plates against the

overlying mantle generates the back-arc volcanism which builds the Andes and the

Rockies. If plates move laterally past each other, then the situation is that of the San

Andreas fault; motion is ‘stick–slip’, just like frictional sliding, and the slip phases

generate large earthquakes.

The concepts of plate motion also tell us about intra-plate processes. At mid-

ocean rises, where two plates peel apart, volcanism occurs, and at particular places

this is manifested at the surface; thus Iceland. In fact, Iceland, like Hawaii, is thought

to be the surface expression of a much deeper mantle excrescence, the mantle plume.

The interplay between plumes and plates is fundamental to the understanding of how

plate tectonics works.

8.1 Plate Tectonics

Plate tectonics describes the division of the Earth’s surface into between thirteen

and twenty plates, and it describes how these plates move relative to each other. It

is essentially a kinematic theory, and the dynamic theory which supports it is the

theory of mantle convection; we will come to that later.

The history of the development of plate tectonics is a fascinating illustration of

the way in which science lurches forwards via the provision of dogma and conﬂict,

A. Fowler, Mathematical Geoscience, Interdisciplinary Applied Mathematics 36,

DOI 10.1007/978-0-85729-721-1_8, © Springer-Verlag London Limited 2011

463

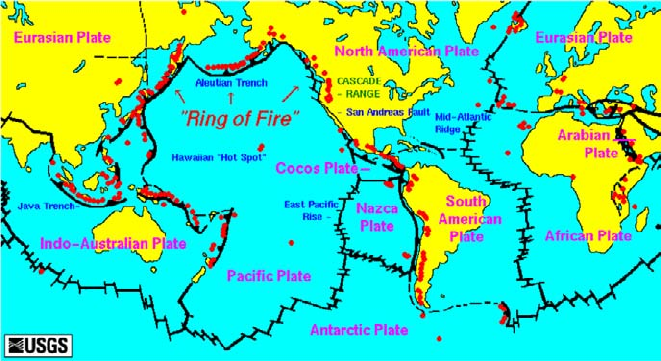
464 8 Mantle Convection

Fig. 8.1 The tectonic plates of the Earth. Image courtesy USGS, see http://vulcan.wr.usgs.gov

and their eventual resolution as the knowledge base increases. Plate tectonics is,

in fact, a very old theory. Its origins lie in the nineteenth century, but it was per-

haps ﬁrst properly formulated as a consistent theory by Alfred Wegener, a German

meteorologist, whose book on the subject was published in 1915.

The basic idea is very simple. Inspection of a map of the globe (see Fig. 8.1)

leads to the observation that the coastlines of the Americas and Africa ﬁt together

very well. (The ﬁt is in fact improved if boundaries are drawn at the edge of the

continental shelves.) This seemingly fortuitous observation gains credibility when

one ﬁnds that Europe and Greenland slot into the jigsaw, and in fact one can plug

the other continents in as well, forming a global continent which now is known

as Pangaea. However, the resulting concept that there used to be a super-continent,

which then broke up into a number of continental ‘plates’, requires more than simply

putting a jigsaw together. Wegener’s contribution lay in supporting the basic concept

with the evidence from a wide variety of separate disciplines, that there were pale-

ontological, paleogeological and paleoclimatic continuities between the now widely

separated parts of the proto-continent. For example, the continuation of the great rift

fault which deﬁnes Loch Ness in Scotland lies in Newfoundland. There are many

examples of such continuations, so much so that geologists had invented the con-

cept of ‘land bridges’ which had previously joined different continents in order to

explain these matches. The presumption was that the bridges had subsequently dis-

appeared when sea levels rose. This is a good example of a scientiﬁc explanation

which is not mathematically coherent, in the following sense: a process is invoked to

explain an observation which is no less mysterious than the observation itself. Con-

tradistinctively, Wegener’s explanation is an example of Occam’s razor; one simple

(but mysterious) hypothesis can explain a whole host of seemingly disconnected

observations.

8.1 Plate Tectonics 465

Wegener’s theory was built around observations, but his discussion of mechanism

was less sophisticated. He imagined continental blocks ploughing through a viscous

substratum, driven by gravitational ‘pole-displacement’ forces. The strength of his

theory was that it uniﬁed a variety of different observations, but his suggestion that

tidal forces were responsible was ridiculed by Jeffreys. It is at this point in the

story that scientiﬁc enquiry lost its sense of rational progress and became polarised,

almost religiously.

Apart from his lack of a satisfactory theoretical mechanism, Wegener’s main

problem appears to have been that he was not a geophysicist, but a meteorologist.

For those trying to do interdisciplinary science a century later, the story is familiar;

scientists are territorial, at the expense, sometimes, of rationality. Jeffreys’ rejection

of Wegener’s hypothesis on the basis of a lack of realistic mechanism was in itself

reasonable (the Earth is made of solid rock for the most part, why should it deform

like a ﬂuid?) but it is also hugely unimaginative. Much of the dogma which pervades

scientiﬁcally accepted thought is based on the premise that things must behave in

ways that we expect. Since what we expect is based on what we experience, mostly

on relatively short time scales, it is difﬁcult to imagine the possibility of unfamiliar

events occurring. Quite simply, it is difﬁcult to imagine the 3000 kilometre deep

mantle being stirred by convection just like a bowl of porridge.

However, there is an analogy for the ﬂuid-like behaviour of rocks. A similar con-

troversy had raged over ﬁfty years earlier in the nascent ﬁeld of glaciology. Louis

Agassiz championed the idea that great ice sheets had covered large parts of Eu-

rope, transporting sediments and, particularly, large (‘erratic’) boulders. Scientists

were well aware that glaciers ﬂowed like huge rivers, despite consisting of appar-

ently solid ice. The fact that ice could ﬂow when its temperature is raised near

to its melting point should have been a clue to a comparable behaviour of crys-

talline rocks, as indeed might be the common observation of deeply folded rock

strata.

Arthur Holmes was one of a number of people who suggested that thermal con-

vection could be the causative mechanism for continental drift, and this is the ac-

cepted mechanism today. Holmes’s original concept of how convection organised

the continents and oceans was ﬂawed—not surprisingly, since at that time very little

was known about how convection works. But Jeffreys would not accept the concept,

and the dogmatic debate carried on till the early 1960s.

The concept of mantle convection which is now accepted is that the Earth’s man-

tle (i.e., the solid part of the Earth consisting of silicate rocks to a depth of 3000 km)

undergoes thermal convection. There are two possible heat sources to drive this con-

vection: ﬁrstly chondritic (i.e., primitive) rocks contain trace elements of radioactive

material which releases sufﬁcient heat to drive convection. Of course, the precise

distribution of the heat source is not known. It is known that radiogenic rocks are

concentrated in the continents, but the extent of such internal heating at great depth

is speculative. In addition, the Earth is cooling. The release of heat from the core is

also sufﬁcient in itself to drive vigorous convection in the mantle.

If we heat a pan of frying oil, two forms of convection can be observed. There

is a cellular structure consisting of boxes of circulating ﬂuid. Hot ﬂuid rises in the

466 8 Mantle Convection

interior of the boxes and cold ﬂuid sinks at their borders. In addition, we can see

isolated mushroom shaped ‘plumes’. When the lower surface is heated, there is a

tendency for hot (thus buoyant) ﬂuid to accumulate and rise through the surrounding

cooler ﬂuid, looking much like a sprouting fungus. These plumes are affected by the

convective circulation, but can be thought of as largely independent.

The Earth’s mantle is a convecting ﬂuid (in that it ﬂows; it is not a liquid). The

plates which comprise the outer surface are the surface expression of an underly-

ing convective circulation. The plates are not uniform, and this is consistent with

vigorous convection, where we see the cell boundaries migrating irregularly (for

example, in the pan of oil). In the mantle, we also have thermal plumes, and where

these impinge on the surface, volcanism occurs. Iceland and Hawaii are the two best

known examples of this.

The rôle of the continents in this story is slightly confusing. The continents are

not themselves the plates, but rather they are carried by the plates. One can think

of them as a kind of residue or scum which is formed on melting mantle rocks; to

understand this we need to discuss petrogenesis brieﬂy.

All rocks in the mantle are silicate rocks, i.e., they contain silica (SiO

), in pro-

portions ranging from about 40% to about 70%. At the lower end of this range, the

rocks are magnesium or iron rich and are called ‘maﬁc’ (or, extremely, ‘ultramaﬁc’).

The typical such rock is basalt. At the other extreme the rocks are silicic, the type ex-

ample being granite. Roughly speaking, maﬁc rocks have higher melting points and

are less viscous when molten; they are also heavier. Hence, when ascending man-

tle rock melts to form magma, it is the lighter, more silicic rocks which remain as

residue. Thus where volcanism occurs, so also does chemical segregation of the par-

ent rocks. It is through this segregation that the lighter continental rocks are formed,

and remain buoyantly on the surface. It ought to be emphasised that the petrology of

the igneous

rocks is extremely complicated chemically; for example, it is clearly

wrong to think of granite as a simple residue when more maﬁc components have

been melted ﬁrst and removed.

The concept of plates and plumes convection works best for sub-oceanic con-

vection; indeed, there is no clear idea of what sub-continental convection is like. We

shall come back to this later (in the notes). The oceanic plates are the surface expres-

sions of a convecting cell; the mantle rock rises beneath mid-ocean ridges, which are

long, pseudo-linear features (examples are the mid-Atlantic ridge or the East Paciﬁc

rise). At the ridge the ﬂow diverges on either side, and the cell terminates normally

at a downwelling, where the surface plate is subducted below an adjoining conti-

nental plate, as for example off the west coast of South America. This circulation

is essentially self-organising; plumes such as those beneath Hawaii and Iceland act

independently. They are normally thought to originate at the core–mantle boundary,

and can occur in a plate interior (Hawaii) or at a mid-ocean ridge (Iceland).

Plates imply rigidity, and the astute reader will be wondering why the surface

plates should behave more or less rigidly (as they are generally conceived to do) if

Further discussion of petrology is given in Chap. 9.

Meaning born of ﬁre.

8.1 Plate Tectonics 467

the mantle behaves viscously; surely there is a contradiction here? It is at this point

in the discussion that we begin to look at the problem from the point of view of

an applied mathematician. Although early theories of mantle convection provided

good quantitative predictions of such things as plate velocity and oceanic heat ﬂux,

the story is not as simple as was at ﬁrst thought; indeed, from the perspective of

modelling, fundamental features of convection are still not yet completely under-

stood.

We begin with the resolution of the query above, why should the plates which

constitute the lithosphere be rigid if they are convecting? The answer to this lies

in the rheology of crystalline rocks. The rate at which they creep depends on tem-

perature, and this rate dependence has been measured. Theoretical considerations

suggest that the process is thermally activated, so that the temperature dependence

is of Arrhenius form (speciﬁcally, η ∝ exp(E

∗

/RT ), where E

∗

is the activation

energy, R is the gas constant, T is absolute temperature, and η is the viscosity.

Measured values of E

∗

for mantle rocks such as olivine are of typical values around

500 kJ mol

−1

, while the gas constant is 8.3 J mol

−1

. It is a simple and illu-

minating exercise to see that the temperature dependence of the viscosity is very

strong. For example, with the values above, and if we take a pre-multiplicative fac-

tor of 10

Pa s (for illustrative purposes), then we ﬁnd that the viscosities at temper-

atures 1500 K, 1000 K, and 500 K, respectively, are approximately 2.8 ×10

Pa s,

1.5 × 10

Pa s and 2.1 ×10

Pa s. The viscosity variation is vast, and it is this

extreme increased stickiness which causes the lithospheric plates to act as if they

are rigid.

We chose the temperature of 1500 K and the corresponding pre-multiplicative

factor in order to give a realistic estimate at the base of the lithosphere, where vari-

ous lines of evidence point to temperatures and viscosities of this order. The surface

temperature is 300 K, but even at 1000 K there is a nine order of magnitude increase

in viscosity above that below the lithosphere. It is true that crustal near-surface rocks

are weaker, and that elastic or brittle behaviour may become more important than

creep there, but it cannot alter the observation that in general the lithosphere must

be much stiffer than the underlying asthenosphere.

Hence the rigidity of the plates.

We now immediately have what may be the

central conundrum of mantle convection. The temperature dependence of the vis-

cosity makes the cold lithosphere rigid. How does convection operate for such a

ﬂuid? We will ﬁnd out in the next section that the onset of convection is controlled

by a dimensionless number called the Rayleigh number, which is a measure of the

ratio of the destabilising buoyancy force to the stabilising viscosity and thermal dif-

fusivity. More generally, the size of the Rayleigh number measures the vigour of

convection. The effect of the convective circulation in a cell is to stir the ﬂuid. In

the absence of convection, a heated lower boundary and cooled upper boundary will

cause a conductive (linear, in a Cartesian geometry) temperature gradient in the cell.

In effect, of course, the plates are not rigid. The ocean ﬂoor is littered with transform faults,

which can be seen as the offsets in Fig. 8.1. The lithosphere deforms in an effectively viscous way

by means of these fractures, which indicates a plastic behaviour of the surface.

468 8 Mantle Convection

As convection increases, this linear gradient is distorted. The interior ﬂuid becomes

more isothermal, steeper thermal gradients develop near the boundaries.

Now suppose the viscosity varies with temperature, so that the cooler ﬂuid is

more viscous. The cooler ﬂuid is at the top of the cell, and is therefore less mobile.

Because it is less mobile, conduction becomes more important, thus the temperature

gradient decreases, and the less mobile lid becomes thicker. The opposite occurs at

the base, whence the hot basal layer becomes thinner. In fact the bulk of the temper-

ature drop across the cell becomes focussed in the upper lid. If the viscosity contrast

across the cell is large enough, then the upper lid becomes virtually stagnant, and

the convection (which can still be vigorous) is conﬁned to a relatively isothermal

core ﬂow beneath.

This behaviour is what we would expect, and it is what we see in laboratory

experiments involving, say, golden syrup. But: it is not what we see in the Earth.

The plates may be (relatively) rigid, but they move. This is clearest with the oceanic

plates (for continental plates, it is less clear, as mentioned above). That in itself is

not a problem, but there is a problem when we come to consider how the plates

descend into the mantle at subduction zones. The oceanic lithosphere (meaning the

thermal lithosphere, i.e., the cool, ‘rigid’ upper boundary layer of the mantle) is

about 100 km thick when it descends at a subduction zone. The uppermost part

of this lithosphere is elastic rather than viscous, and the detailed bathymetry at a

subduction zone can indeed be understood via the mechanics of a buckling beam.

However, this does not explain how the lithosphere can creep round the corner.

A worse problem is the initiation of subduction. If convection can occur below a

stagnant lid, what is the mechanism whereby the lid begins to subduct?

This might seem a rather abstruse question, since presumably the Earth has

evolved from a much hotter initial state in which the problem of the stagnant lid

may not have been important, and the question of interest is how (and if) subduc-

tion ceases. It becomes less abstruse when we come to consider tectonics on Venus.

Venus is a planet much like the Earth (except for its atmosphere), and we should

presumably expect a similar tectonic habit. But plate tectonics is apparently absent

from Venus. And so we have the question: why should subduction occur on the

Earth but not on Venus?

Actually, things are worse (and thus more interesting) than this. It appears (from

meteor impact counts) that the surface of Venus is of relatively uniform age, about

300–500 million years, much younger than the planet. A possible inference is that

planetary resurfacing occurred in that previous epoch through a rapid plate tectonic

cycle, and then ceased.

Has it ceased for ever, or is plate tectonics episodic on

Venus? What will happen on Earth? We will provide glimpses of possible answers to

these questions in this chapter, but ﬁrst, we begin at the beginning with a discussion

of the mathematical basis for the theory of thermal convection.

Another possibility is that volcanic activity caused the resurfacing.

8.2 Rayleigh–Bénard Convection 469

8.2 Rayleigh–Bénard Convection

The classical study of thermal convection considers the motion of a ﬂuid bounded by

two horizontal plates, at z =0 and z =d, say, and heated from below, for example by

prescribing the upper and lower temperatures to be T

and T

, where the temperature

difference across the cell T

−T

> 0. The Navier–Stokes equations which describe

the motion are

+∇.(ρu) =0,



+(u.∇)u



=−∇p +∇.τ −ρg

(8.1)

where ρ is the density, u is the ﬂuid velocity, p is the pressure, τ is the deviatoric

stress tensor, and g is the downwards acceleration due to gravity. In the mantle, one

might suppose g would vary, but in fact it is relatively constant. The linear decrease

with depth that one would ﬁnd for a constant density is almost exactly compensated

by the fact that the Earth’s core is much denser than the mantle. The assumption of

a Cartesian geometry is obviously not appropriate for the mantle, but it is not likely

that this will make a substantial qualitative difference to the results.

In mantle convection, it is often held that the heat source should be internal (ra-

dioactive) heating. The reason for this supposition appears to be largely historical,

following Holmes’s original suggestion. While it is true that radiogenic heating may

be important, it is not necessary, since the Earth is cooling, and the heat released

from the core is also well able to provide the necessary heating from below.

In Eqs. (8.1), we require constitutive relations for ρ as a function of T and p (the

equation of state) and τ (the rheology). We suppose that ρ is given by

ρ =ρ

[1 −αT +βp], (8.2)

where T is temperature, α is the thermal expansion coefﬁcient, and β is the com-

pressibility; ρ

is a reference density. In the mantle, the value of α is 3 ×10

−5

−1

and it decreases somewhat with depth. The assumption of a constant compressibility

coefﬁcient β is an oversimpliﬁcation but will sufﬁce. With a change in pressure of

some 1200 kbar, the density changes from about 3.5 × 10

kg m

−3

to 5.6 kg m

−3

which implies βρ

gd ≈1.6 (since pressure is essentially lithostatic).

We suppose that the rheologic equation of state is deﬁned by a viscosity η, so that

the components of the stress tensor are given by (we use the summation convention)

=η



∂u

∂x

∂u

∂x

−

∂u

∂x



=2η



˙ε

−

div u



, (8.3)

where ˙ε

is the strain rate tensor. In general, η is a function of temperature, pressure

and stress, but to begin with we will take it as a constant, η

. (Later we will use η

as a viscosity scale.)

The ﬁnal equation we require is the energy equation. This is

ρc

−αT

=∇.[k∇T ]+ρQ +

2η

, (8.4)