Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

470 8 Mantle Convection

where d/dt denotes the material derivative ∂/∂t +u.∇, c

is the speciﬁc heat at con-

stant pressure, k is the thermal conductivity, Q is the (radiogenic) internal heating

(units are W kg

−1

), and the last term is the viscous heat dissipation. The advection

and conduction terms will be familiar, the others being neglected in normal labora-

tory circumstances. In the Earth, we cannot necessarily assume they are negligible,

however.

8.2.1 Boundary Conditions

The Earth’s mantle lies above the liquid outer core and below the ocean or astheno-

sphere. Since the viscosity of the mantle is enormous, the effective boundary condi-

tions which are appropriate are those of no shear stress. More generally, the stresses

are continuous, and in particular the jump in the shear stress is zero at top and bot-

tom. The mantle shear stress is effectively zero if the viscosity above or below is

very small; but strictly this also relies on the fact that velocity gradients in the ocean

or core are not correspondingly large. Without doubt this is the case.

For most of our discussion we will consider only two-dimensional motion in the

(x, z) plane; generalisation to the third dimension is easy to effect. In this case we

also deﬁne the velocity components via u =(u, 0,w). The boundary conditions we

thus apply are the following:

∂u

∂z

=w =0,T=T

at z =0;

∂u

∂z

=w =0,T=T

at z =d.

(8.5)

Lateral conditions (in x) are also strictly necessary. Since our initial concerns are

with stability, where we select modes of various horizontal wave numbers, it is of

less importance to enunciate these.

8.2.2 Non-dimensionalisation

We choose the obvious space scale d and the temperature scale T

. One (but not

the only) natural velocity scale is the thermal velocity scale

, where the thermal

diffusivity scale κ

is given by

, (8.6)

and k

is a reference value of the thermal conductivity; the corresponding thermal

time scale is d

/κ

. Finally, the pressure and stress scales are chosen to balance the

pressure gradient with the viscous terms, of order ηu/d ∼ η

(where η

is a

reference value for the viscosity), except that the lithostatic pressure is subtracted

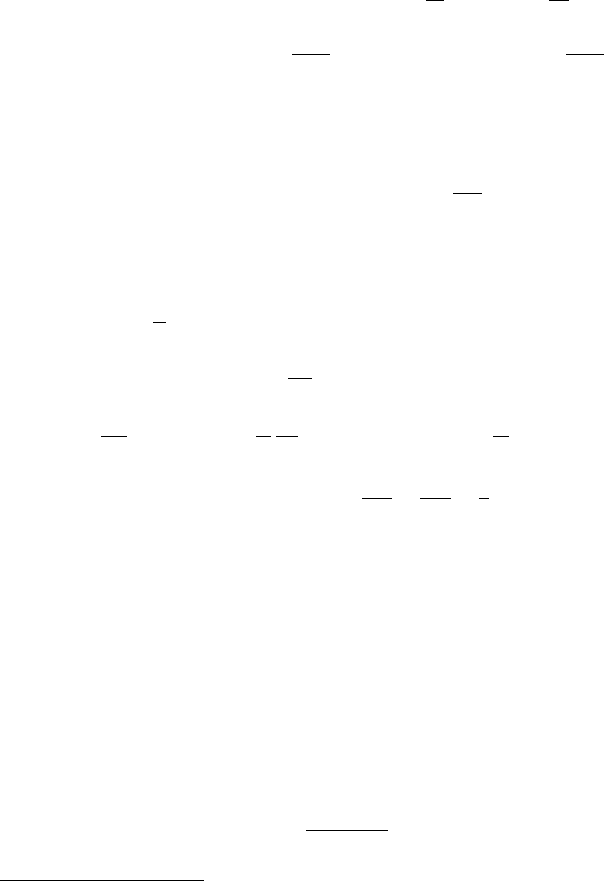
8.2 Rayleigh–Bénard Convection 471

off ﬁrst. This lithostatic pressure is that which occurs in the absence of motion, and

is not directly relevant to the convective motion; we will determine it shortly.

Thus we write

x =dx

∗

,T=T

∗

,η=η

∗

, u =

∗

,t=

∗

k =k

∗

,p=ρ

gd ¯p(z

∗

) +

∗

,ρ=ρ

∗

, τ =

∗

(8.7)

substitute these variables into the governing equations, and hence derive the fol-

lowing dimensionless model, written in full vector form, and where we omit the

asterisks for convenience:

ρ =¯ρ(z) −BT +

¯ρ =1 +C ¯p,

+∇.(ρu) =0,





+(u.∇)u



=−∇p +∇.τ +

k[RT −Cp],

∂ ¯p

∂z

=−(1 +C ¯p),

−DT



w ¯p





=∇.[k∇T ]+ρH +

=η



∂u

∂x

∂u

∂x

−

∇.u



(8.8)

where the second stress invariant is deﬁned as

2τ

=τ

. (8.9)

The parameters are a Boussinesq number

B =αT

, (8.10)

a barometric number

C =βρ

gd, (8.11)

the Rayleigh number

R =

αT

, (8.12)

The Rayleigh number is normally deﬁned with T =T

−T

, on the basis of scaling the temper-

ature as T = T

+T T

∗

, but we avoid this here because the later introduction of a temperature-

dependent viscosity makes the present deﬁnition less cumbersome. For the mantle, we have

∼T in any case.

472 8 Mantle Convection

the Prandtl number

σ =

, (8.13)

the dissipation number

D =

αgd

, (8.14)

and an internal heating number

H =

. (8.15)

The solutions will therefore depend on the six parameters above, together with the

temperature ratio

. (8.16)

8.2.3 Boussinesq Approximation

The values of α and T

for the mantle are about 3 ×10

−5

−1

and 3500 K. (The

core–mantle boundary is thought to be at a temperature of 3500 K, or greater.) For

these values B ≈0.1, and as α decreases with depth, B will decline somewhat with

depth. The Boussinesq approximation is associated with the limit B →0, and pro-

vides a major simpliﬁcation of the model. We have already estimated the parame-

ter C as being of order 1.6, while the Rayleigh number for the mantle is of order

(and generally is always large when convection occurs in environmental ﬂows).

Therefore also BC/R 1, and so

ρ ≈¯ρ(z). (8.17)

The Boussinesq approximation actually goes further; it assumes that variations

in density can be neglected, except in the buoyancy term (this is the term RT in

the momentum equation). In particular, it assumes C is small, which is inevitably

true in laboratory experiments, but is not accurate for the mantle. Nevertheless, we

proceed by supposing that C is small; then

¯ρ =1, ¯p =1 −z (8.18)

and thus

∇.u ≈0; (8.19)

the ﬂuid is approximately incompressible.

The Prandtl number is the ratio of the kinematic viscosity η

/ρ

to the thermal

diffusivity. In the Earth’s mantle, this is huge (of order 10

) and the corresponding

8.2 Rayleigh–Bénard Convection 473

acceleration terms are utterly negligible. For liquids and gases, the Prandtl num-

ber is generally of O(1); it is quite large for some oils, and low for metals (e.g.,

mercury). We suppose that σ  1. The dissipation number D is negligible in the

laboratory. In the mantle, with α = 3 × 10

−5

−1

, g = 10 m s

−2

, d = 3000 km,

= 10

Jkg

−1

,wehaveD ≈ 0.9. The decrease of α with depth causes D

to decrease also, but it is clearly not negligible in the Earth. Again, we begin by

neglecting it. In any event, the viscous heating term of order D/R can generally be

safely neglected.

The heating parameter H depends on the assumed distribution of radioactive

elements in the mantle. For a value of Q = 1pWkg

−1

(1 picowatt = 10

−12

W),

and ρ

=4 ×10

kg m

−3

, d =3000 km, k

=4Wm

−1

, T

=3500 K, we ﬁnd

H ∼10; essentially of O(1), but as we shall see in due course, relatively small when

convection is vigorous.

If we take the scaled viscosity and thermal conductivity to be constant (η =k =1),

and put the parameters B,C,σ

−1

,D and H equal to zero, then we obtain the

Boussinesq equations of thermal convection:

∇.u = 0,

∇p =∇

u +RT

k, (8.20)

+u.∇T =∇

with associated boundary conditions for free slip:

T =1, u.n =τ

=0onz =0,

T =0, u.n =0onz =1,

(8.21)

where τ

represents the shear stress, and we can take the surface temperature to be

zero by a mild rescaling of the temperature.

8.2.4 Linear Stability

In the absence of motion, u =0, the temperature proﬁle is linear,

T =1 −z, (8.22)

and the lithostatic pressure is modiﬁed by the addition of

p =−

(1 −z)

. (8.23)

To study small perturbations to this basic state, we deﬁne a stream function ψ for

two-dimensional motion via

u =−ψ

,w=ψ

. (8.24)

474 8 Mantle Convection

(The sign is opposite to the usual convention; for ψ>0 this describes a clockwise

circulation.) We also deﬁne the temperature perturbation θ by

T =1 −z +θ. (8.25)

Eliminating the pressure gradient by cross differentiation, we ﬁnd

∇

ψ +Rθ

=0,

−ψ

+ψ

=∇

θ,

(8.26)

and the boundary conditions are

=ψ =θ =0onz =0, 1. (8.27)

The linear stability of the basic state is determined by neglecting the nonlinear

advective terms in the heat equation. We then seek normal modes of wave number

k in the form

ψ =f(z)e

σt+ikx

θ =g(z)e

σt+ikx

(8.28)

whence f and g satisfy



−k



f +ikRg =0,

σg −ikf =



−k



(8.29)

where D =d/dz, and

f =g =0onz =0, 1. (8.30)

By inspection, solutions are

f =sin nπz, g =b sin nπ z, (8.31)

(n =1, 2,...) providing

σ =

)

−





, (8.32)

which determines the growth rate for the nth mode of wave number k.

Since σ is real, instability is characterised by a positive value of σ . We can see

that σ decreases as n increases; therefore the value n = 1 gives the most unstable

value of σ .Also,σ is negative for k → 0ork →∞, and has a single maximum.

Since σ increases with R, we see that σ>0 (for n =1) if R>R

, where

(π

)

. (8.33)

8.3 Nonlinear Stability; Planforms 475

In turn, this value of the Rayleigh number depends on the selected wave number k.

Since an arbitrary disturbance will excite all wave numbers, it is the minimum value

of R

which determines the absolute threshold for stability. The minimum is ob-

tained when

k =

√

, (8.34)

and the resulting critical value of the Rayleigh number is

27π

≈657.5; (8.35)

That is, the steady state is linearly unstable if R>R

For other boundary conditions, the solutions are still exponentials, but the coef-

ﬁcients, and hence also the growth rate, must be found numerically. The resultant

critical value of the Rayleigh number is higher for no-slip boundary conditions, for

example, (it is about 1707), and in general, thermal convection is initiated at values

of R

∼

O(10

8.3 Nonlinear Stability; Planforms

Linear stability analysis does not inform us as to the subsequent development of the

unstable convective mode. This is the domain of nonlinear stability theory, or bifur-

cation theory. There are three questions we can use this theory to address. Firstly,

does the convective mode saturate at a small but ﬁnite amplitude (supercritical bi-

furcation) or is there a sudden transition to a large amplitude solution? The basis for

the alternatives lies in the solution of the Landau equation

A +k

|A|

A, (8.36)

which we expect to derive via a multiple scales analysis (and we will do so below).

In (8.36), A is the (complex) amplitude of the principal convective mode at R =R

When the steady state is unstable (Re k

> 0), then supercritical bifurcation occurs

if Re k

< 0.

In Bénard’s original experiments, he found hexagonal convective cells. More

generally, two-dimensional convective rolls (as we have been describing) can be

unstable to three-dimensional motions; for example, hexagons are a superposition

of three sets of rolls, square cells are a superposition of two sets. It is clear that the

two-dimensional linear stability analysis has a degeneracy, as the roll orientation is

unconstrained. In particular, we might examine the evolution of two or more sets of

rolls. We would expect that their amplitudes A

,...would then be described by

coupled sets of Landau equations, whose solution would determine the preference

for rolls, hexagons, or other planforms.

The ﬁnal question which multiple scales analysis can address is the evolution of

the plan form over long space scales. Vagaries of initial conditions can lead to the

476 8 Mantle Convection

onset of (for example) rolls of differing orientations in different parts of a large ﬂuid

container. The subsequent evolution of the resultant dislocations can be described

by a spatial version of the Landau equation, which in some circumstances produces

the famous Ginzburg–Landau equation.

These issues are certainly relevant to convection theory, but they are something

of a sideshow here, as convection in the Earth’s mantle (and any other large scale

geophysical system: the Earth’s core, magma chambers, the oceans, the atmosphere)

occurs at high Rayleigh number, well beyond the range of applicability of the small

amplitude theories. We will begin by deriving the Landau equation in some detail,

and then discuss more brieﬂy its generalisations to study planforms and dislocations.

8.3.1 Landau Equation

We begin by returning to the nonlinear Boussinesq model of two-dimensional con-

vection in (8.26) and (8.25):

∇

ψ +Rθ

=0,

−ψ

+ψ

=∇

θ,

(8.37)

together with θ = ψ =0onz = 0 and z = 1. The procedure of nonlinear stability

theory is straightforward and we do not dwell on it here. Essentially, when R is close

to (and above) R

, so that R − R

= ε

,say,withε  1, then a convective mode

of amplitude O(ε) will grow on a time scale of O(ε

). The critical mode which is

excited has wave number k

=π/

√

2, but in fact a side band in which k −k

=O(ε)

(since R

has a quadratic minimum at k

) is excited; it is then natural to expect slow

variation also on space scales of O(1/ε). We return to slow spatial variation later.

The method of multiple scales now proceeds by deﬁning

R =R

+sε

t =ε

(8.38)

(where s =±1 to allow for supercritical or subcritical bifurcations), and seeking

perturbation expansions for θ and ψ in the form

ψ =εψ

+ε

+···,

θ =εθ

+ε

+···.

(8.39)

In general, the functions depend on both the fast and slow scales t and τ . Since the

basic convective mode is steady, we can here ignore the fast time scale altogether,

thus we suppose ψ

and θ

are functions of τ ,aswellasx and z.

8.3 Nonlinear Stability; Planforms 477

Substituting the expansions into (8.37), we obtain a sequence of problems for ψ

and θ

when we equate terms of order ε

, n =1, 2, 3,.... In succession, these are





=0, (8.40)

where the linear operator L is deﬁned by



∇

∂

∂x

∂

∂x

∇



, (8.41)

and then





≡



−ψ







≡



−sθ

1τ

+{ψ

−ψ

+ψ

−ψ

}



(8.42)

and so on. Suitable boundary conditions are that (ψ

,θ

)

= (0, 0)

on z = 0 and

z =1.

The marginally stable solution of wave number k

can be written as (suppression

of the fast time scale t suppresses all the stable modes)





A(τ )e



−i



sinπz+(cc), (8.43)

where (cc) denotes the complex conjugate, and β is given from (8.29) when σ = 0

β =

√

3π

. (8.44)

Here, A(τ ) is the unknown amplitude of the motion; in general it may be com-

plex, but we anticipate that here it is in fact real. Speciﬁcally, then,

=A sin k

x sin πz,

=βAcos k

x sin πz,

(8.45)

and thus

−ψ

πA

sinπzcos πz. (8.46)

In order to solve (8.42)

, note that if

v =





ipk

sin qπz, (8.47)

478 8 Mantle Convection

then

Lv =L

v, (8.48)

where



)

ipk

−(p

)



. (8.49)

Now (ψ

,θ

)

satisﬁes







πA



sin2πz, (8.50)

and therefore





= L

−1



πA



sin2πz



−

24π



sin 2πz. (8.51)

(There is also an arbitrary multiple of (ψ

,θ

)

, but this term is irrelevant in calcu-

lating A(τ ).)

What is important in solving for (ψ

,θ

)

is to determine the secular terms on

the right hand side of (8.42), which are those proportional to e

sin πz. Note that

=0, and the remnant nonlinear term in (8.42)

is (since θ

=0)

(sinπz−sin 3πz)cos k

x, (8.52)

and thus







−

isA

βA





sin πz+(cc) +harmonics. (8.53)

In general, this has no bounded solution; thus in order to obtain such a solution, the

right hand side must be orthogonal to the adjoint of the linear operator L. Equiva-

lently, we can ﬁnd a bounded solution to (8.53) of the form









sin πz+(cc) +harmonics (8.54)

providing







−

isA

βA





, (8.55)

8.3 Nonlinear Stability; Planforms 479

and this can be solved only if the right hand side is orthogonal to the null vector of

∗

, the adjoint of L

(since det L

=0).

We have

∗



+π

)

−ik

−(k

+π

)



, (8.56)

with null vector

η =



+π

)



; (8.57)

hence the orthogonality condition for solvability at O(ε

) requires (since the inner

product (v, w) =v

w, where

w is the complex conjugate of w)

dτ



3(k

+π

)



A −

. (8.58)

When s =1 (thus R =R

+ε

), this can be written as the Landau equation

dτ

9π

A −

; (8.59)

the bifurcation is supercritical, and the equilibrium amplitude is A =

√

3π

8.3.2 Plan Forms

Bénard’s original experiments showed cellular convection occurring in hexagons,

formed by the superposition of three sets of rolls at 120° to each other. In other

situations, one sees square cells. Since the orientation of rolls is arbitrary, an obvious

problem is to extend the preceding nonlinear analysis to the consideration of several

sets of skewed rolls.

To do this, we need to write the equations of motion in a suitable three-

dimensional form. By analogy with the deﬁnition of a stream function, we deﬁne

the vector potential A via

u =curl A, divA =0; (8.60)

A is deﬁned up to the addition of the gradient of a harmonic function. Denote the

components of A via

A =(−φ,ψ,ω), (8.61)

so that

u =(ω

−ψ

, −φ

−ω

,ψ

+φ

). (8.62)