Fowler A. Mathematical Geoscience
Подождите немного. Документ загружается.


480 8 Mantle Convection
Taking the curl of (8.20)
2
and writing T =1 −z +θ , we find
∇
4
φ +Rθ
y
=0,
∇
4
ψ +Rθ
x
=0,
∇
4
ω =0,
φ
x
=ψ
y
+ω
z
,
∇
2
θ +ψ
x
+φ
y
=θ
t
+(ψ
x
θ
z
−ψ
z
θ
x
)
+(φ
y
θ
z
−φ
z
θ
y
) +(ω
y
θ
x
−ω
x
θ
y
),
(8.63)
and the boundary conditions are
θ =0,
[τ
13
∝]ω
zy
−ψ
zz
+ψ
xx
+φ
xy
=0,
[τ
23
∝]−ω
xz
−φ
zz
+φ
yy
+ψ
xy
=0,
ψ
x
+φ
y
=0,
(8.64)
on z =0 and z =1.
We note from (8.63)
1−3
that ∇
4
(−φ
x
+ψ
y
+ω
z
) =0. Therefore the compatibil-
ity condition −φ
x
+ψ
y
+ω
z
=0 is automatically satisfied if we apply the boundary
conditions
φ
x
=ψ
y
+ω
z
,
φ
xz
=ψ
yz
+ω
zz
,
(8.65)
on z =0, 1. In particular, we can eliminate ω from the other boundary conditions so
that (using also (8.64)
4
)
∇
2
φ =∇
2
ψ =θ =ψ
x
+φ
y
=0onz =0, 1, (8.66)
and the model reduces to the form
L
⎛
⎝
ψ
φ
θ
⎞
⎠
=
⎛
⎝
−ε
2
θ
x
−ε
2
θ
y
θ
t
+u.∇θ
⎞
⎠
, (8.67)
where
ε
2
=R −R
c
, (8.68)
and
L=
⎛
⎜
⎜
⎝
∇
4
0 R
c
∂
∂x
0 ∇
4
R
c
∂
∂y
∂
∂x
∂
∂y
∇
2
⎞
⎟
⎟
⎠
, (8.69)
8.3 Nonlinear Stability; Planforms 481
and u.∇θ is given from the right hand side of the last equation in (8.63). We can
then find ω by quadrature from the compatibility condition.
The linearised system at R =R
c
is simply L(ψ,φ,θ)
T
=0, and particular solu-
tions are rolls aligned in the y and x directions:
φ =ω =0,ψ=A sin k
c
x sin πz, θ =βAcos k
c
x sin πz,
ψ =ω =0,φ=B sink
c
y sin πz, θ =βB cos k
c
y sin πz.
(8.70)
Of course other oblique rolls exist, having
ω =0,θ=βC cos
k
c
(x cos α +y sin α)
sinπz,
ψ =C cosα sin
k
c
(x cos α +y sin α)
sin πz,
φ =C sinα sin
k
c
(x cos α +y sinα)
sin πz,
(8.71)
but we suppose now that the leading order solution consists of just two sets of or-
thogonal rolls. Specifically, we write as before
R =R
c
+ε
2
,t=ε
2
τ,
ψ =εψ
1
+ε
2
ψ
2
+···,
φ =εφ
1
+ε
2
φ
2
+···,
ω =εω
1
+ε
2
ω
2
+···,
θ =εθ
1
+ε
2
θ
2
+···,
(8.72)
and by equating powers of ε, we obtain the equations for the vectors w
i
=
(ψ
i
,φ
i
,θ
i
)
T
,
Lw
1
=0,
Lw
2
=(0, 0,N
2
)
T
,
Lw
3
=(−θ
1x
, −θ
1y
,θ
1τ
+N
3
)
T
,
(8.73)
where the nonlinear terms are
N
2
=[ψ
1x
θ
1z
−ψ
1z
θ
1x
]+[φ
1y
θ
1z
−φ
1z
θ
1y
]+[ω
1y
θ
1x
−ω
1x
θ
1y
], (8.74)
and
N
3
=[ψ
1x
θ
2z
−ψ
1z
θ
2x
]+[ψ
2x
θ
1z
−ψ
2z
θ
1x
]
+[φ
1y
θ
2z
−φ
1z
θ
2y
]+[φ
2y
θ
1z
−φ
2z
θ
1y
]
+[ω
1y
θ
2x
−ω
1x
θ
2y
]+[ω
2y
θ
1x
−ω
2x
θ
1y
]. (8.75)
482 8 Mantle Convection
The two roll solution we select is
ω
1
=0,ψ
1
=A(τ ) sin k
c
x sin πz,
θ
1
=β[A cos k
c
x +B cosk
c
y]sin πz, φ
1
=B(τ)sin k
c
y sin πz,
(8.76)
representing two orthogonal sets of rolls.
We now omit the subscript c on k
c
for convenience. From (8.74) and (8.76), we
find
N
2
=βkπ
1
2
A
2
+B
2
+AB coskx cos ky
sin 2πz. (8.77)
Let us denote
v
pqr
=e
ipkx+iqky
sin rπz; (8.78)
then if c is constant,
L(cv
pqr
) =(L
pqr
c)v
pqr
, (8.79)
where
L
pqr
=
⎛
⎜
⎝
δ
2
0 ipkR
c
0 δ
2
iqkR
c
ipk iqk −δ
⎞
⎟
⎠
, (8.80)
and
δ =
p
2
+q
2
k
2
+r
2
π
2
. (8.81)
From (8.73) and (8.77), w
2
satisfies
Lw
2
=
1
2
βkπ
A
2
+B
2
ˆ
θv
002
+
1
4
βkπAB
ˆ
θ
v
112
+v
1,−1,2
+(cc)
, (8.82)
where
ˆ
θ =(0, 0, 1)
T
, (8.83)
and hence we find the particular solution (using the fact that βk =
1
3
)
w
2
=
1
6
π
A
2
+B
2
a
002
v
002
+
1
12
πAB
a
112
v
112
+a
1,−1,2
v
1,−1,2
+(cc)
, (8.84)
where a
pqr
=L
−1
pqr
ˆ
θ. The inverse of the matrix L
pqr
is
L
−1
pqr
=
1
|L
pqr
|
⎛
⎜
⎝
q
2
k
2
R
c
−δ
3
−pqk
2
R
c
−ipkR
c
δ
2
−pqk
2
R
c
p
2
k
2
R
c
−δ
3
−iqkR
c
δ
2
−ipkδ
2
−iqkδ
2
δ
4
⎞
⎟
⎠
, (8.85)
where
|L
pqr
|=δ
2
p
2
+q
2
k
2
R
c
−δ
3
, (8.86)

8.3 Nonlinear Stability; Planforms 483
and thus
a
pqr
=
δ
2
|L
pqr
|
⎛
⎜
⎝
−ipkR
c
−iqkR
c
δ
2
⎞
⎟
⎠
. (8.87)
We write a
pqr
= (α
pqr
,β
pqr
,γ
pqr
)
T
, and for the particular values of p, q,r in
(8.84), we have
a
002
=
⎛
⎜
⎝
α
002
β
002
γ
002
⎞
⎟
⎠
=
⎛
⎜
⎝
0
0
−
1
4π
2
⎞
⎟
⎠
,
a
112
=
⎛
⎜
⎝
α
112
β
112
γ
112
⎞
⎟
⎠
=
1
573π
2
⎛
⎜
⎝
27ik
27ik
−100
⎞
⎟
⎠
,
a
1,−1,2
=
⎛
⎜
⎝
α
112
−β
112
γ
112
⎞
⎟
⎠
.
(8.88)
In particular,
φ
2x
=
1
12
πAB sin 2πz
ikβ
112
(v
112
−v
1,−1,2
) +(cc)
,
ψ
2y
=
1
12
πAB sin 2πz
ikα
112
(v
112
−v
1,−1,2
) +(cc)
,
(8.89)
which are equal since α
112
=β
112
; hence ω
2z
=φ
2x
−ψ
2y
=0, and
ω
2
=0. (8.90)
Next, we calculate the secular terms in (8.75). We have
ψ
1
=A sin kx sin πz,
φ
1
=B sin ky sin πz,
θ
1
=β[A cos kx +B cosky]sin πz,
(8.91)
and also
⎛
⎝
ψ
2
φ
2
θ
2
⎞
⎠
=
⎡
⎣
1
6
π
A
2
+B
2
⎛
⎝
0
0
γ
002
⎞
⎠
+
1
3
πAB
⎛
⎝
−a cosky sin kx
−a coskx sin ky
γ
112
cosky cos kx
⎞
⎠
⎤
⎦
sin 2πz,
(8.92)
where we have written
α
112
=β
112
=ia, (8.93)
484 8 Mantle Convection
and a = 9k/191π
2
is real. We are only interested in the secular terms in N
3
, and
these are terms in e
ikx
sin πz or e
iky
sin πz. Successively, we find
ψ
1x
θ
2z
=−
1
6
π
2
kAsin πz
A
2
+B
2
γ
002
coskx +γ
112
AB cos ky
+···,
−ψ
1z
θ
2x
=
1
12
π
2
kγ
112
A
2
B sin πzcosky +···,
ψ
2x
θ
1z
=−
1
12
βkπ
2
aAB sin πz(Acos ky +B coskx) +···,
−ψ
2z
θ
1x
=
1
6
βkπ
2
aA
2
B sin πzcos ky +···,
(8.94)
and the corresponding φ terms can be found by swapping A with B and x with y.
Summing the terms in (8.94) and adding the corresponding φ terms, we find that
the secular terms are
N
3
=−[N
101
v
101
+N
011
v
011
]+(cc) +···, (8.95)
where
N
101
=
1
12
π
2
kγ
002
A
A
2
+B
2
+
1
24
π
2
kγ
112
AB
2
,
N
011
=
1
12
π
2
kγ
002
B
A
2
+B
2
+
1
24
π
2
kγ
112
A
2
B.
(8.96)
Noting that
θ
1
=
1
2
βAv
101
+
1
2
βBv
011
+(cc), (8.97)
the equation for w
3
can be written (from (8.73))
Lw
3
=
⎛
⎜
⎝
−
1
2
ikβA
0
1
2
βA
−N
101
⎞
⎟
⎠
v
101
+
⎛
⎜
⎝
0
−
1
2
ikβB
1
2
βB
−N
011
⎞
⎟
⎠
v
011
+(cc) +···, (8.98)
and the particular solution is
w
3
=w
101
v
101
+w
011
v
011
+(cc) +···, (8.99)
providing
L
101
w
101
=
⎛
⎜
⎝
−
1
2
ikβA
0
1
2
βA
−N
101
⎞
⎟
⎠
,L
011
w
011
=
⎛
⎜
⎝
0
−
1
2
ikβB
1
2
βB
−N
011
⎞
⎟
⎠
. (8.100)
8.3 Nonlinear Stability; Planforms 485
Now
L
101
=
⎛
⎜
⎝
δ
2
0 ikR
c
0 δ
2
0
ik 0 −δ
⎞
⎟
⎠
,L
011
=
⎛
⎜
⎝
δ
2
00
0 δ
2
ikR
c
0 ik −δ
⎞
⎟
⎠
, (8.101)
where
δ =π
2
+k
2
. (8.102)
The adjoint matrices are
L
∗
101
=
⎛
⎜
⎝
δ
2
0 −ik
0 δ
2
0
−ikR
c
0 −δ
⎞
⎟
⎠
,L
∗
011
=
⎛
⎜
⎝
δ
2
00
0 δ
2
−ik
0 −ikR
c
−δ
⎞
⎟
⎠
, (8.103)
and the respective null vectors are
η
101
=
⎛
⎜
⎝
ik
0
δ
2
⎞
⎟
⎠
, η
011
=
⎛
⎜
⎝
0
ik
δ
2
⎞
⎟
⎠
. (8.104)
Therefore the solvability condition for (8.100), that the right hand sides are orthog-
onal to the corresponding null vectors of the adjoint, implies the Landau equations
(remember that (η, f) =η
T
¯
f, do not forget to take the conjugate of f)
−
1
2
βk
2
A +δ
2
1
2
βA
−N
101
=0,
−
1
2
βk
2
B +δ
2
1
2
βB
−N
011
=0.
(8.105)
Simplification, using
k =
π
√
2
,βk=
1
3
,γ
002
=−
1
4π
2
,γ
112
=−
100
573π
2
, (8.106)
leads to
dA
dτ
=
2
9π
2
A −
π
2
16
A
A
2
+cB
2
,
dB
dτ
=
2
9π
2
B −
π
2
16
B
B
2
+cA
2
,
(8.107)
which generalises (8.59). The value of c is
c =
773
573
. (8.108)

486 8 Mantle Convection
It is straightforward to analyse (8.107) using phase plane analysis. There are two
solutions corresponding to rolls
(A, B) =(A
∗
, 0) or (0,A
∗
), (8.109)
where
A
∗
=
4
√
2
3π
2
, (8.110)
and a square cell solution
A =B =
A
∗
(1 +c)
1/2
. (8.111)
The square cell solution is stable if c<1 and unstable if c>1 (see Question 8.9).
Hence it is (just) unstable. This is in line with conventional wisdom, which has it
that only rolls are stable, and the breakdown to three-dimensional motion occurs at
higher Rayleigh number. It is also thought that non-Boussinesq effects (e.g., tem-
perature dependence of fluid properties) can cause square cells or hexagons to be
stable at the onset of convection.
8.3.3 Dislocations and Chaos
A different use of nonlinear stability theory is in tracking the evolution of convection
patterns over long space scales. In general, we would want to allow the orientation
of rolls to vary slowly in space, but here we restrict ourselves to the two-dimensional
case where the orientation is fixed, and only the cell size, velocity and temperature
vary slowly in space as well as time. To be specific, we consider rolls pointing in the
y direction, but we generalise the treatment at the beginning of this section to allow
for slow variation in the x direction.
We define the slow space variable
X =εx, (8.112)
so that x derivatives become
∂
∂x
→
∂
∂x
+ε
∂
∂X
, (8.113)
and the Laplacian and biharmonic operators become
∇
2
→∇
2
+2ε
∂
2
∂X∂x
+ε
2
∂
2
∂X
2
,
∇
4
→∇
4
+4ε∇
2
∂
2
∂X∂x
+ε
2
2∇
2
+4
∂
2
∂x
2
∂
2
∂X
2
+···.
(8.114)

8.3 Nonlinear Stability; Planforms 487
With the operator L still defined by (8.41), we have
L→ L
0
+εL
1
+ε
2
L
2
+···, (8.115)
where L
0
is just as in (8.41), and
L
1
=
4
∂
∂x
∇
2
R
c
12
∂
∂x
∂
∂X
, L
2
=
2
∂
2
∂z
2
+6
∂
2
∂x
2
0
01
∂
2
∂X
2
. (8.116)
Next we expand w =(ψ, θ)
T
as
w =εw
1
+ε
2
w
2
+···, (8.117)
and we define N
20
and N
30
as in (8.42), and we define
N
21
=
0
ψ
1X
θ
1z
−ψ
1z
θ
1X
; (8.118)
expanding in powers of ε, we derive the sequence of equations
L
0
w
1
=0,
L
0
w
2
=N
20
−L
1
w
1
,
L
0
w
3
=N
30
+N
21
−L
1
w
2
−L
2
w
1
.
(8.119)
The solution for w
1
isgivenby(8.43), and with w
20
defined by (8.51), we have
L
0
w
20
=N
20
. (8.120)
Now we need to find a particular solution to the equation
L
0
w
21
=−L
1
w
1
=r
11
A
X
e
ikx
sinπz+(cc), (8.121)
where
r
11
=
3
4
π
2
k
1
6
i
. (8.122)
This is given by
w
21
=v
21
A
X
e
ikx
sinπz+(cc), (8.123)
where
L
11
v
21
=r
11
, (8.124)
L
11
being defined through (8.49). This is only possible if r
11
⊥ η givenby(8.57),
and, on doing the calculation, we find that it is(!). The solution is then given up to
488 8 Mantle Convection
addition of a multiple of w
1
which we can ignore; the particular solution we use is
w
21
=
0
−
i
9π
2
A
X
e
ikx
sin πz+(cc). (8.125)
We can thus define w
2
as
w
2
=w
20
+w
21
. (8.126)
It remains to find the secular-producing terms proportional to e
ikx
sin πz (and its
conjugate) on the right hand side of (8.119)
3
. We easily find that there are no such
terms in L
1
w
20
, and that N
21
=0. As before (cf. (8.53)),
N
30
=
−
1
6
iA
1
2
βA
τ
+
1
48
kA
3
e
ikx
sin πz+···, (8.127)
while
L
1
w
21
=
−
3
4
iπ
2
2k
9π
2
A
X
e
ikx
sin πz+···, (8.128)
and finally
L
2
w
1
=
5
2
iπ
2
1
2
β
A
XX
e
ikx
sinπz+···. (8.129)
The coefficient of e
ikx
sin πz on the right hand side of (8.119) must be orthogonal
to η given by (8.57). Computing the inner product, we find that this requires that A
satisfy the Ginzburg–Landau equation
∂A
∂τ
=
2
9π
2
A −
π
2
16
A
3
+4
∂
2
A
∂X
2
. (8.130)
In deriving (8.130), we made the tacit assumption that A was real. More gener-
ally, one derives the same equation, but in the general form
∂A
∂τ
=k
1
A +k
2
|A|
2
A +D
∂
2
A
∂X
2
, (8.131)
and in other systems, the coefficients may be complex.
8.4 High Rayleigh Number Convection
We have seen that convection occurs if the Rayleigh number is larger than O(10
3
) in
general, depending on the precise boundary conditions which apply. In the Earth’s
mantle, suitable values of the constituent parameters are α = 3 ×10
−5
K
−1
, T
b
=
3500 K, ρ
0
= 3 ×10
3
kg m
−3
, g = 10 m s
−2
, d = 3000 km, η
0
= 10
21
Pa s, κ
0
=
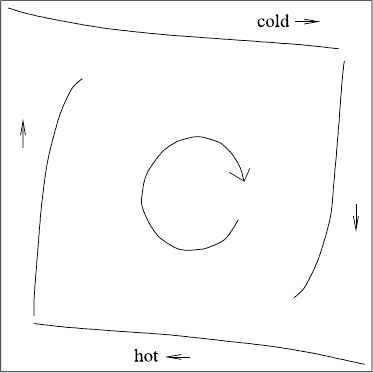
8.4 High Rayleigh Number Convection 489
Fig. 8.2 Schematic
representation of boundary
layer convection
10
−6
m
2
s
−1
, and for these values, the Rayleigh number is about 0.85 ×10
8
. Thus
the Rayleigh number is much larger than the critical value, and as a consequence we
can expect the convection to be vigorous (if velocities of centimetres per year can
be said to be vigorous).
There are various intuitive ways in which we can get a sense of the likely be-
haviour of the convective solutions of the Boussinesq equations when R 1. Since
R multiplies the buoyancy term, any O(1) lateral temperature gradient will cause
enormous velocities (this is best seen in (8.26) rather than (8.12)). One might thus
expect the flow to organise itself so that either horizontal temperature gradients are
small, or they are confined to thin regions, or both. Since O(1) temperature varia-
tions are enforced by the boundary conditions, the latter is more plausible, and thus
we have the idea of the thermal plume, a localised upwelling of hot fluid which will
be instantly familiar to glider pilots and seabirds.
A mathematically intuitive way of inferring the same behaviour follows from
the expectation that increasing R drives increasing velocities; then large R should
imply large velocity, and the conduction term in the heat equation u.∇T =∇
2
T is
correspondingly small. Since the conduction term represents the highest derivative
in the equation, its neglect would imply a reduction of order, and correspondingly we
would expect thermal boundary layers to exist at the boundaries of the convecting
cell. This is in fact what we will find: a hot thermal boundary layer adjoins the
lower boundary, and a cold one adjoins the upper boundary, and a rapid circulation
in the interior of the cell detaches these as upwelling and downwelling plumes. The
general structure of the resulting flow is shown in Fig. 8.2. We analyse this structure
in the following sections.
