Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

510 8 Mantle Convection

Slab Stress As ζ →−∞in the delamination layer, we have, from (8.191),

θ ∼Γζ, T

∼−



Γζ

Ψ ∼







n−2

Γζ

(8.247)

If we deﬁne

z =1 −νZ (8.248)

in the lid, so that the lid base is at Z =s, then (8.247) becomes

θ ∼−

Γ(s−Z)

∼−





s −Z



Ψ ∼





(s −Z)

2ε



n−2

exp



−

Γ(s−Z)



(8.249)

and in addition, from (8.190),

P ∼−



s −Z



∼−s





s −Z



N ∼



2ε



Γ |(s −Z)



n−2

exp



Γ(s−Z)



(8.250)

We thus rescale the variables as follows:

θ =−

(1 −T)

,P=

,N=ε

2(n−1)

exp



(1 −T)

εT



,Ψ=

exp



−

(1 −T)

εT



Ψ +

exp



−

(1 −T

)

εT



(x).

(8.251)

The re-deﬁnition of Ψ merits some discussion. We add the term in λ to allow for the

small non-zero surface velocity. We anticipate that λ is of algebraic order in ε, and

so it will only be important at the surface. We include the term separately because it

is distinct from the other part of the stream function, proportional to exp(θ/ε).

8.5 Variable Viscosity 511

Substitution of (8.251)into(8.174)(via(8.188)) leads to (on omitting the over-

tildes)

=ν

−T

−P

=ν

) −(1 −T),

=2ε

N exp



(1 −T)

εT



∂

∂x∂Z



exp



−

(1 −T)

εT



Ψ +···



=−ε

N exp



(1 −T)

εT



∂

∂Z

−ν

∂

∂x



exp



−

(1 −T)

εT



Ψ +···



∗2

+ν

N =

∗n−1

2n+1



∂T

∂x

∂

∂Z

−

∂T

∂Z

∂

∂x



Ψ exp



−

(1 −T)

εT



+···



∂

∂Z

+ν

∂

∂x

(8.252)

where the dots denote the extra term λ exp[−(1 −T

)/εT

]Zu

, which can be ne-

glected except near the top surface Z =0.

Ignoring λ, the heat equation is

2n+1

exp



−

(1 −T)

εT



[Ψ

−Ψ

∂

∂Z

+ν

∂

∂x

, (8.253)

and we see that convection is formally negligible as ε →0, as we suppose. In prac-

tice, the value of Pe =ε

−(2n+1)

exp[−(1 −T)/εT] (a kind of Péclet number) at the

surface, where T = T

= 0.2 for the Earth, is approximately ε

−8

−4/ε

if n = 3.5,

and for our preferred value of 0.023, this is about 4 ×10

−63

.ThevalueofT where

Pe = is



1 +(2n +1)ε ln





+ε ln







, (8.254)

and for moderate <1 and n =3.5, T



≈0.59. Thus the high value of n and low ε

combine to yield a viscous structure which is only truly rigid for T<T



. Figure 8.5

illustrates this by plotting the approximating viscosity function

app

(T ) =



1 −T



n−1

exp



1 −T

εT



(8.255)

(gleaned from (8.250)) for ε = 0.023, n =3.5. Evidently, the formal limit N

app

exp[O(1/ε)] only occurs practically for T

∼

0.7, and advection is only truly negli-

gible for T

∼

0.6. Some inaccuracy can be expected in the theory.

Neglecting advection, we have the approximate conductive proﬁle (for ν 1)

T ≈T

(1 −T

(8.256)

512 8 Mantle Convection

Fig. 8.5 The

pseudo-viscosity function

app

(T ) = (

1−T

)

2n−1

exp{

1−T

εT

for n =3.5andε =0.023

and thus P and T

, satisfying

≈−T

−P

≈−(1 −T),

(8.257)

together with the matching conditions (from (8.249)) P,T

→0asZ →s,aregiven

P =−

(1 −T

)

(s −Z)

=−

(1 −T





−s

Z +



(8.258)

We are unable to satisfy the condition of zero shear stress at the top surface Z =0,

since there is a residual shear stress there given by

=−

(1 −T

)ss



. (8.259)

In order to enforce T

= 0atZ = 0, the shear stress must change rapidly in a

boundary layer near Z = 0. Why should such a boundary layer exist? Notice that

we also require the stream function to vanish, i.e. Ψ =0atZ = 0. To solve for Ψ ,

we expand the expressions for T

and T

in (8.252). If we put

V(T)=

1 −T

≈

(1−T

−1, (8.260)

8.5 Variable Viscosity 513

then we ﬁnd

=2N



Ψ −ε(V

Ψ +V

) +ε

+ε

λ exp



(V −V

)/ε







=−N



Ψ −ε(2V

Ψ)+ε



+ν



Ψ −ε(2V

Ψ)+ε

+ε

λ exp



(V −V

)/ε







(8.261)

where V =V

at T =T

. Away from Z =0, we have

≈2NV

Ψ, T

≈−NV

Ψ, (8.262)

thus Ψ =0atZ =0. The presence of a term ε

in (8.261) suggests the existence

of a boundary layer of thickness ε over which Ψ can drop to zero. It is in order to

get the shear stress T

to zero as well that we introduced the extra stress term in λ.

Deﬁne a boundary layer variable ξ by

Z =εξ. (8.263)

Noting that V

and V

are O(1), we have to leading order, from (8.261),

=O(1) +2Nε

λ exp







=−N



Ψ −2V

+Ψ

ξξ





,ν



(8.264)

where

Z=0

=−

(1 −T

)

. (8.265)

Now we rescale P and T

in this stress boundary layer in order that T

can

change. This necessitates writing

P =

∗

εν

∗

, (8.266)

so that

∗

−T

3ξ

−P

∗

=δ

1ξ

−ε

(1 −T),

(8.267)

and at leading order we have

∗

=−T

∗

(8.268)

(to match to P

∗

→0asξ →∞), and thus

3ξ

=2T

∗

. (8.269)

514 8 Mantle Convection

We can enforce the scaling T

∼1/εν

by choosing ε

λN ∼1/εν

in (8.264)

and then, since νT

∼ 1/εν = 1/δ  T

= O(1), N = 1/T

∗n−1

≈ (1/νT

)

n−1

∼

n−1

; thus we choose

λ =

εδ

n+1

. (8.270)

This is algebraic in ε as we required (provided one does not examine a limit in which

Ra =exp[O(1/ε)] or n ∼1/ε).

It follows from (8.264) that, since Nε

λ ∼1/εν

1,

∗

≈

∗

n−1

exp



−







, (8.271)

whence

∗

≈2

exp



−



ξ/n





−1



. (8.272)

Using (8.270), this gives

∗



−1





exp



−

(1 −T

)ξ



, (8.273)

and the solution for T

(sf )





1 −e

−Bξ/s



−

2fs



ξe

−Bξ/s

, (8.274)

where

B =

1 −T

,f=2



−1





. (8.275)

The matching condition is that T

→ T

givenby(8.259). This implies 2(sf )



, hence



s|u



−1







=−



(1 −T

)

3nT





. (8.276)

We require u

=0atx =0 and x =a. A ﬁrst integral is

s|u



−1





−s



, (8.277)

where

A =

(1 −T

)

12nT

, (8.278)

and s =s

where u



=0. It follows that u

> 0, and









−s



−1



−s



dx, (8.279)

8.5 Variable Viscosity 515

and we choose s

so that u

=0atx =a,i.e.









−s



−1



−s



dx =0. (8.280)

Skin Stresses Looking back, we see from (8.279), (8.188), (8.251) and (8.266)

that in the stagnant lid, the dimensional shear stress

∼

, (8.281)

but within the (boundary layer) skin, the pressure and normal stresses are higher,

,τ

∼

δRa

. (8.282)

Since P

∗

≈0, the largest stress is thus the horizontal stress −p

+τ

≈2τ

Speciﬁcally, at the surface, (8.250) implies that the horizontal stress σ

=2τ

ξ=0

δRa







−1





δRa





(1 −T

)

6nT

−s

)

. (8.283)

It is extensional (σ

> 0) near the upwelling (x = 0) and compressive near the

downwelling.

We can calculate an estimate for the size of the stress,

[σ

δ(1 −T

)

6nT

αρ

gdT

(8.284)

using our previous estimates. We take n = 3.5, T

= 0.2, α = 3 × 10

−5

−1

= 1500 K, ρ

= 3 × 10

kg m

−3

, g = 10 m s

−2

, d = 3000 km; if we choose

κ = 10

−6

−1

and η

= 10

Pa s, then Ra ≈ 3.6 × 10

;ifε = 0.023, then

δ ≈ 0.013, and we compute [σ

]=8 kbar (1 kilobar = 10

bar = 10

Pa). This

is a huge stress, comparable to the breaking strength of rock, and is suggestive of

the idea that, within the conﬁnes of a purely viscous rheology such as we have here,

some realistic adaptation of the model should be made.

8.5.5 Summary

What have we discovered? For a purely viscous ﬂuid with strong Arrhenius depen-

dence on temperature, high Rayleigh number convection occurs as vigorous ﬂow

driven by small excess temperatures below a stagnant lid. This is clearly seen in

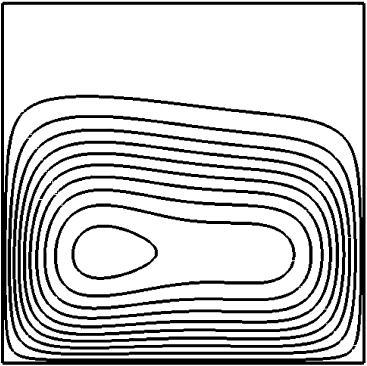
516 8 Mantle Convection

Fig. 8.6 Stream function

contours of a

temperature-dependent

viscosity convection

calculation at Rayleigh

number 10

, the viscosity

scaled to that at the basal

temperature. The rheology is

that of (8.176), with Λ =1,

n =1, ε =0.2. Basal and

surface dimensionless

temperatures are 1 and 0.1,

respectively. The absence of

contours towards the top

indicates the stagnant lid.

Figure courtesy Mike

Vynnycky

Fig. 8.6. In this lid, the stresses are high, and they increase rapidly in a narrow layer

near the surface. But, as with constant viscosity convection, the analysis is compli-

cated, and in parts unresolved.

At the outset, we do not even know the appropriate value of the rate-controlling

internal viscosity η

and temperature T

in the asthenosphere; a convoluted argu-

ment leads to their determination by (8.186) and (8.187), in terms of the unknown

temperature excess φ

at the base. The delamination layer below the lithosphere

is described by (8.191), and this introduces further unknowns: the lithosphere base

s(x), the lithospheric temperature gradient Γ , and the far ﬁeld stress S

∞

(x).Of

these, Γ is given by the slab temperature ﬁeld via (8.199), and S

∞

is given (in

principle) by the extra condition for the outer thermal layer in (8.211).

The core ﬂow requires the determination of two further quantities, the plume

buoyancy constants C

and C

. Given these, then the plume/thermal boundary layer

equation (8.206) with boundary conditions (8.207) can be solved, subject to the

pseudo-periodicity condition (8.213), which in addition yields the plume head tem-

perature φ

(Ψ ) used in the outer thermal layer equations. Three extra conditions

are necessary to determine φ

, C

and C

, and in addition s must be prescribed.

We may suppose (8.212) determines C

;givens,(8.215) determines C

, and

ﬁnally (8.214) determines φ

. Of course, all of these relations are coupled, hence

the intent of the untangling discussion following (8.215).

The determination of s apparently forms part of the solution of the delamina-

tion equations (8.191). Further study of these equations is undoubtedly warranted.

The existence of the approximating similarity solution suggests that this is the case,

although the appropriate boundary condition for s at x =0 is less clear.

8.6 Subduction and the Yield Stress 517

8.6 Subduction and the Yield Stress

We have now arrived at the central conundrum of plate tectonics, alluded to in

Sect. 8.1. At high values of Ra and low values of ε, vigorous convection occurs

beneath a stagnant lid. Active plate tectonics does not occur in the model, as it does

on the Earth. In the lid, the stresses become extremely large, of the order of kilo-

bars, and this provides the clue to resolve the conundrum. We argue that at cold

temperatures and at such high stresses, viscous behaviour breaks down, and the

ﬂow becomes plastic. In order to describe this, we need to reconsider the rheology

of mantle rocks in the vicinity of the Earth’s surface.

8.6.1 Near-Surface Mantle Rheology

We have already described, in Sect. 8.5.1, the viscous rheology of polycrystalline

rocks. At low temperatures, and for short time behaviour (associated with seismic

waves, for example), the mantle is elastic, and a common description of both elastic

and creeping behaviours can be represented by assuming a Maxwell viscoelastic

ﬂuid, whose constitutive law can be represented schematically by the equation

˙ε =

2η

˙τ

, (8.285)

where η is the viscosity given by (8.163), τ is the stress, and E

is an elastic mod-

ulus. (We dispense with the details of tensor representation.) The ratio

2η

(8.286)

thus deﬁnes a Maxwell time scale, such that for changes on a time scale t  t

the behaviour is elastic, and on longer time scales t t

, the behaviour is viscous.

Note that the Maxwell time depends on temperature and stress.

Into this mixture we now add the concept of failure. Brittle failure is associated

with the coalescence of microcracks within the rock, and is classically associated

with an internal friction of the material. Thus brittle failure is usually associated

with the attainment of a failure stress

=Kp, (8.287)

where p is the lithostatic pressure, and K is a dimensionless coefﬁcient of friction

of O(1).

Geophysicists often combine these two ideas of viscous creep and brittle failure

to propose a failure diagram such as that shown in Fig. 8.7. This identiﬁes the yield

stress with the minimum of two values, one of which is the brittle failure stress τ

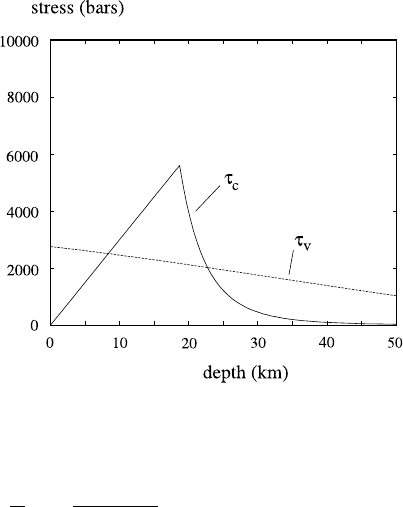
518 8 Mantle Convection

Fig. 8.7 Brittle (straight full

line) and ductile (curved full

line) yield stress τ

function of depth. The dashed

line represents a typical

corresponding lithospheric

shear stress using the

boundary layer theory for a

purely viscous mantle, with

highly temperature-dependent

viscosity

and the other is a so-called ductile failure stress τ

determined from the viscous

rheology (8.163), thus



˙ε

exp



∗

+pV

∗



, (8.288)

and τ

depends on temperature and strain rate. Figure 8.7 shows a typical yield

curve τ

=min(τ

,τ

) using a typical mantle strain rate and temperature proﬁle as

a function of depth.

The interpretation of Fig. 8.7 is that if the stress τ (often taken to be deﬁned by the

second stress invariant 2τ

=τ

) is less than τ

, then deformation is elastic, but

if the stress reaches τ

, then it remains on the yield surface, and the deformation is

plastic. The diagram in Fig. 8.7 then looks reassuringly familiar to the yield surface

of critical state soil mechanics, with the brittle yield resembling the tension failure or

Hvorslev yield surface, and the ductile yield resembling the Roscoe yield surface.

It has to be said that the use of this diagram in this way represents a misleading

misinterpretation of the classical ideas of yield and plasticity, and it should really be

outlawed.

Firstly, the use of (8.287) is based on Byerlee’s law, which was developed to

describe rock friction and not yield in the classical plastic sense of continuing de-

formation at a critical stress. It is actually clear that the Earth’s mantle exhibits yield

at much lower stresses. For example, the motion of deep subducting slabs is by

a stick–slip motion facilitated by slip events between the descending slab and the

overlying mantle. These slip events indicate yield at a stress τ

which can be calcu-

lated, since it is due to the buoyant excess weight of the subducting slab, and such

estimates suggest τ

∼

300 bars, much less than one would calculate from (8.287).

Secondly, the ductile part of the curve in Fig. 8.7 is not a yield curve at all, since

it describes ﬂow behaviour at a pre-assigned strain rate. Since the strain rate is part

of the ﬂow problem requiring solution, this part of the curve is truly meaningless.

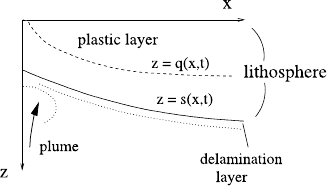
8.6 Subduction and the Yield Stress 519

Fig. 8.8 An illustration of

the region of plastic yield

within the lithosphere,

assuming a viscoplastic

rheology

Despite this, the ‘yield’ curve is often used to divide the upper mantle into a

plastic upper part (with brittle yielding), an elastic middle part, and a ductile lower

part. Such inferences appear to be groundless.

I want to propose a different kind of rheology which is consistent with observa-

tions of fault motion by earthquakes. This is that plastic yield should occur at a yield

stress τ

, which we will take to be typical of stress release in earthquakes, and much

less than the brittle Byerlee value. In essence, we associate this kind of failure with

subcritical crack propagation, and we do not distinguish necessarily between elastic

and viscous behaviour for stresses less than τ

. We can in fact allow a viscoelastic

deformation for τ<τ

, but it turns out that the elastic deformation is inessential to

the description, and we henceforth omit it.

Our rheology is thus viscoplastic, and takes the form

=2η ˙ε

, (8.289)

where the viscosity η isgivenby(8.163)ifτ<τ

, and is determined in the plastic

case by the requirement that τ =τ

on the yield surface.

8.6.2 The Plastic Lid: Failure and Subduction

It is now possible to carry forward the boundary layer analysis of Sect. 8.5 to allow

the description of a plastic lid within the lithosphere, but we forgo the dubious plea-

sure of tormenting the reader further with this, interesting and intricate though the

analysis is. We conﬁne ourselves to a description of the results.

The essential novelty is indicated in Fig. 8.8, which indicates that where the

stresses in the lithosphere exceed the yield stress, there is a plastic lid of dimension-

less (scaled with νd) depth q. In this lid, the material behaves plastically, while the

part of the lithosphere below the plastic lid is viscous. Intricacies include the fact

that there are boundaries at top and bottom of the lid (of thickness O(ε) relative to

the lid scale) in which the stresses jump.

From the analysis, we obtain relations for s as before, and also for the plastic lid

depth q. The analysis assumes a stagnant lid, and is thus self-consistent if q<s.

The reason for this has to do with the effective viscosity in the plastic lid. Our

assumption for the ﬂow rule when the yield stress is reached is that increments of