Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

560 9 Magma Transport

while the momentum equation is

=η



−



, (9.23)

whence p = p

is constant, and at r = a, a force balance implies −p

+2η

−p

, thus

C =−

−p

2η

. (9.24)

The constitutive law for p

−p

now follows from consideration of the kinematic

boundary condition for the solid ﬂow which applies at the pore boundary. To relate

our cylindrical void to macroscopic quantities, we suppose it is encased in a grain

of dimension l (speciﬁcally, a cylinder of length l and radius l) so that φ = a

The rate of melting is S (mass per unit volume per unit time). This corresponds to a

rate of removal (or ablation) at the pore boundary of

v =

2ρ

(9.25)

(because S/ρ

is the volume removed per unit volume per unit time, and this is equal

to 2πalv/πl

). Finally, the kinematic boundary condition for a is that

˙a =u|

+v, (9.26)

and in terms of macroscopic variables, this becomes (since

φ =2a ˙a/l

)

φ =

−

−p

)φ

. (9.27)

The time derivative

φ represents the derivative following the grain, i.e.

φ = φ

u.∇φ.

(9.31) applies if the grain viscosity is constant, i.e., diffusion creep prevails. For

the more likely dislocation creep with a ﬂow law given by

˙ε

=Aτ

n−1

, (9.28)

and 2τ

=τ

, we ﬁnd that (9.24) is replaced by

=−

−p

n−1

−p

). (9.29)

Note that this reduces to (9.24) when n =1, since then A =1/2η

. The correspond-

ing form of (9.27)is

φ =

−

2Aφ

−p

n−1

−p

). (9.30)

9.4 Melt Transport in the Asthenosphere 561

A viscous prescription for the solid matrix would be

=−p

δ +2η

, (9.31)

where

is the solid strain rate. In (9.21), we effectively regain the mantle momen-

tum equation

∇.



(1 −φ) +ρ



k, (9.32)

because (as we shall ﬁnd) φ  1, and we can suppose p

− p

∼

¯σ

.Themain

effect of partial melting on the circulation is in the buoyancy term in (9.32), where

1% partial melting (φ =0.01) is equivalent to a buoyancy temperature difference of

300 K (if the thermal expansion coefﬁcient is α =3 ×10

−5

−1

Lastly, there is an energy equation for each phase. These equations are analogous

to the two momentum equations, with a huge interfacial heat transport term, which

consequently implies the two phases have locally equal temperatures. The other

equation then follows from the equation of total energy conservation. The simplest

form of this is

LS +ρ

(1 −φ)

+ρ

+αT



+(1 −φ)



=K∇

T, (9.33)

where L is the latent heat, and we take the speciﬁc heats c

and c

, and averaged

thermal conductivity K = K

(1 − φ) + K

φ to be constant; the time derivatives

d/dt

and d/dt

are equal to ∂/∂t + v.∇ and ∂/∂t + u.∇, respectively. Various

small dissipative terms have been neglected in (9.33).

9.4.1 Summary

The equations we propose to describe the partial melt region are thus

T =T

+Γp



+∇.(φv)



=S,



−φ

+∇.



(1 −φ)u



=−S,

v −u =−Π

φ[∇p

+ρ

k],

0 =−∇(φp

) +∇.



(1 −φ)



−



φ +ρ

(1 −φ)



+u.∇φ =

−

φ(p

−p

)

=−p

δ +2η

LS +(1 −φ)



−αT



+φ



−αT



=K∇

(9.34)

Boundary conditions for these equations will be described in due course.

562 9 Magma Transport

9.4.2 Simpliﬁcation

We anticipate that φ 1. Then we have, from (9.34)

∇.u ≈0, (9.35)

and

∇.

≈



φ +ρ

(1 −φ)



k. (9.36)

Apart from the added buoyancy term, the solid matrix ﬂow equations are contiguous

with those of the mantle outside the partial melt zone, and it is convenient to suppose

that u and p

can thus be determined independently of φ. In particular, p

is in any

case approximately lithostatic, and thus

∇p

≈−ρ

k. (9.37)

In order to proceed, we want to non-dimensionalise these equations. We guess,

or anticipate, that the adiabatic terms are less important than the advective terms in

the energy equation, and that heat conduction is small. We also anticipate that v u

(melt velocity is rapid) but φv u (melt ﬂux is small). Then in the energy equation,

LS ≈−ρ

Γdp

/dt

. The constitutive relation for the effective pressure p

−p

suggests that it is balanced by the melt rate, thus p

−p

∼η

S/ρ

φ. We anticipate

that this stress is less than lithostatic stress, and this in turn suggests p

≈p

. With

these assumptions we scale the variables as

x ∼d, u ∼u

, v ∼[v],t∼d/[v],φ∼[φ],S∼[S],

(9.38)

where d is a suitable length scale for the partial melt zone, and we write

−[p]ψ, (9.39)

and put

−ρ

gz, (9.40)

where z is the height above a convenient reference level.

Our choice of balances in the equations then suggests

[φ][v]

=[S],

[v]=Π

[φ](ρ

−ρ

)g,

[p]=

[S]

[φ]

[S]=

(9.41)

9.4 Melt Transport in the Asthenosphere 563

Table 9.6 Assumed values of constants

Symbol Meaning Typical value

g gravity 10 m s

−2

matrix density 3 ×10

kg m

−3

melt density 2.5 ×10

kg m

−3

L latent heat 3 ×10

Jkg

−1

Γ Clapeyron slope 10

−7

KPa

−1

α thermal expansion coefﬁcient 3 ×10

−5

−1

ambient melting temperature 1500 K

K thermal conductivity 4 W m

−1

matrix viscosity 10

Pa s

b tortuosity 10

grain size 2 ×10

−3

melt viscosity 1 Pa s

, c

speciﬁc heats 10

Jkg

−1

mantle ascent velocity 10

−9

−1

(3 cm y

−1

)

d melt zone depth 10

m (10 km)

ρ ρ

−ρ

0.5 ×10

kg m

−3

and these determine the unknowns [φ], [v], [S] and [p]; explicitly

[φ]≡μ =



ρ



Γu



1/2

, [v]=ρ



ρ c

Γu

dΠ



1/2

, (9.42)

where ρ =ρ

−ρ

. We can now examine whether the assumption that [φ][v]

[v] is valid.

We use the values of the constants in Table 9.6. From these we ﬁnd

μ =[φ]∼0.24 ×10

−2

, [v]∼4.8 ×10

−8

−1

(1.5my

−1

[S]∼3 ×10

−11

kg m

−3

−1

(9.43)

and thus [φ][v]∼1.2 ×10

−10

−1

, u

∼ 10

−9

−1

, [v]∼4.8 ×10

−8

−1

vindicating our assumptions.

Dimensionless equations for the partial melt variables are then

+∇.(φv) =S,

v −δu =φ[

k +ν∇ψ],

(1 +r)[φ

+δu.∇φ]=S −φψ,

S +(1 −μφ)



(δ

−1

∂

+u.∇)(−z −˜νψ) +λ

θw



(1 −λ

θ)(∂

+v.∇)(−z −˜νψ) =−ε∇

ψ,

(9.44)

564 9 Magma Transport

where w =u.

k, and the parameters are deﬁned by

St =

T

,T=ρ

gdΓ,

δ =

[v]

,ε=

K[p]

ν =

[p]

ρgd

, ˆν =

[p]

αT

,λ

αT

,r=

ρ

(9.45)

and also θ = T/T

. Using Table 9.6,wehaveT ∼ 30 K, [p]∼4 ×10

Pa, and

thus

St ∼10,δ∼0.02,ε∼1.2 ×10

−3

,ν∼0.8,

˜ν ∼0.12,λ

s,l

∼0.15,r∼0.2.

(9.46)

On this basis, we neglect relatively small terms proportional to μ, λ

, St

−1

in the

energy equation (the last two mainly for simplicity):

+δ∇.(φu) +∇.



{

k +ν∇ψ}



=S,

(1 +r)[φ

+δu.∇φ]+φψ =S,



−1

∂

∂t

+u.∇



(z +˜νψ) −ε∇

ψ =S.

(9.47)

Further simpliﬁcation results from the equation for conservation of mass of solid

(9.34)

, which can be written in the dimensionless form

∇.u =μ∇.(φu) +



(1 +r)φ

−

1 +r



. (9.48)

Neglecting terms of O(μ),(9.47)

can be written as

+δu.∇φ +∇.



{

k +ν∇ψ}



=S, (9.49)

and combining this with (9.47)

gives

2φφ

+ν∇.



∇ψ



=φψ +rφ

, (9.50)

where we also neglect the advective derivative of φ,ofO(δr).

Finally, combination of (9.49) with (9.47)

yields



−1

∂

∂t

+u.∇



(z +˜νψ −δφ) −∇.



{

k +ν∇ψ}



=ε∇

ψ. (9.51)

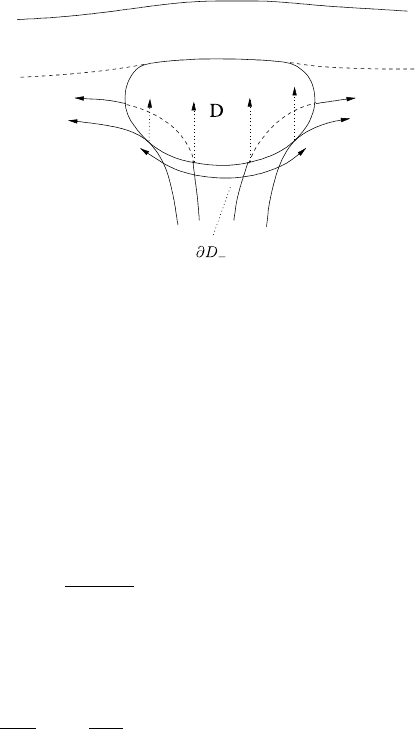
9.4 Melt Transport in the Asthenosphere 565

Fig. 9.14 Schematic

illustration of the domain D.

The lower part of the

boundary ∂D

−

is indicated;

on this we would expect to

prescribe φ =0

A comment on the parameters ε, ν and ˜ν is in order. From (9.45), these are

proportional to [p], which in turn is proportional (via (9.41)) to η

. We took

= 10

Pa s in Table 9.6, reﬂecting the typical inferred asthenospheric viscos-

ity (e.g., from postglacial rebound studies). The consequent inferred grain stress is

then large (400 bars), which for typical dislocation creep laws would suggest effec-

tive viscosities about three to four orders of magnitude lower. Such lower viscosities

are not inconsistent with global asthenospheric values, since melting occurs locally.

In turn they would suggest lower values of [p], which in turn would reduce the low-

ering of viscosity via nonlinear creep. A more consistent way to guess grain stress

values is to use the nonlinear closure law (9.30), which implies, for n =1,

[p]=n



[S]

2Aρ

[φ]



1/n

. (9.52)

If we identify η

=1/2Aτ

n−1

, where τ is a typical asthenospheric shear stress, say

10 bars, then (9.52) can be written as

[p]



[p]



1/n

, (9.53)

where [p]

is the pressure scale for ﬂow exponent n.Forn = 3.5, for example,

[p]

3.5

≈100 bars, and ν, ˜ν and ε would be a factor of four lower. It is therefore not

unreasonable to think of ν as being small also, and we will adopt this strategy in our

analysis below.

9.4.3 Boundary Conditions

Equations (9.47)

3,4

are to be solved for φ and ψ in a domain which we can expect

to resemble that shown in Fig. 9.14.

Both (9.50) and (9.51) are hyperbolic equations for φ if ψ is known. It is there-

fore natural to suppose that we should prescribe φ on those parts of the boundary

566 9 Magma Transport

where the characteristics enter the domain. The physically appropriate condition

would seem to be

φ =0on∂D

−

, (9.54)

where ∂D

−

denotes that part of the boundary ∂D of D on which u.n < 0, where n

is the outward normal to D, and this appears consistent with the choice of apparent

characteristics for (9.51), if this is written in the form (using (9.50))



−1

∂

∂t

+u.∇



(z +˜νψ −δφ) =φψ +rφ

+ε∇

ψ. (9.55)

If this is an appropriate condition for φ, then the elliptic (9.47)

suggests that

ψ should be prescribed on ∂D, except where φ = 0 and the elliptic term for ψ is

degenerate. Since the melting temperature is T

+Γp

in the partially molten region,

while it is T

+ Γp

in the cold mantle, it seems we should ensure continuity of

temperature by having p

on ∂D,i.e.ψ =0on∂D (φ =0). The two boundary

conditions can be combined in the form

φψ =0on∂D. (9.56)

While this is plausible, it is by no means certain, and one might expect the non-

degenerate elliptic ψ term in (9.55) to require ψ to be prescribed everywhere. This

is an example of a model where some functional analysis would actually be useful.

A further difﬁculty is that to say the melting temperature in the cold mantle is

+ Γp

carries in itself no meaning, since equilibrium melting temperature is

deﬁned through thermodynamic equilibrium at the interface. In addition, we should

add that (9.56) has not been systematically derived from any physical principle. We

now attempt to resolve this latter issue.

9.4.4 Thermodynamic Equilibrium

At the microscopic interface between partially molten and cold mantle ∂D,were-

quire that the jump in temperature, pressure and Gibbs free energy be zero:

[T ]

=[p]

=[G]

=0. (9.57)

The ﬁrst of these is standard, the second is a force balance (it should properly be a

balance of normal stress, but we omit deviatoric stresses for simplicity), while the

third is the condition of thermodynamic equilibrium, and it is this condition which

we need to prescribe, instead (perhaps) of (9.56).

Consider ﬁrst a reference state in which p

= p

in the partial melt region. The

Gibbs free energy of each separate phase depends on temperature and pressure, and

we can write for the partial melt side of ∂D, G =G

, where

=φ(h

−TS

) +(1 −φ)(h

−TS

), (9.58)

9.4 Melt Transport in the Asthenosphere 567

in which h

and S

are the speciﬁc enthalpies and entropies of each phase. In this

reference state, p =p

on the cold side, and therefore on this side G =G

, where

−TS

. (9.59)

The enthalpies and entropies are evaluated at the interfacial temperature T and in-

terfacial pressure p =p

. The jump in G across the boundary is

G =[G]

=φ[h −TS], (9.60)

where h =h

−h

, S =S

−S

, and this is zero since the latent heat L =h =

TS; []

represents the jump across ∂D from cold to partially molten.

Now suppose we change p

, p

and φ away from the reference state, by amounts

δp

,δp

and δφ. On the cold side, the force balance condition implies

δp

=δp

−δ



φ(p

−p

)



, (9.61)

and thus

δG

= v

δp

−S

δT

= v

δp

−S

δT −v



φ(p

−p

)



, (9.62)

whereas on the molten side

δG

= δφ[h −TS]+φ(v

δp

−S

δT )

+(1 −φ)(v

δp

−S

δT ). (9.63)

Using the fact that δG

=δG

and h =TS, we get

−v



φ(p

−p

)



=φ



δp

−S

δT ) −(v

δp

−S

δT )



. (9.64)

Now the right hand side is φ[δG

− δG

], where G

and G

are the local spe-

ciﬁc Gibbs free energies of liquid and solid within the mush. We are assuming

that thermodynamic equilibrium prevails locally at the pore-grain interface so that

δG

= δG

(which is in fact equivalent to the Clapeyron relation T = T

+ Γp

);

therefore the assumption of macroscopic thermodynamic equilibrium [G]

=0im-

plies δ[φ(p

−p

)]=0, and since φ(p

−p

) =0 in the reference state, the condi-

tion we prescribe is

φ(p

−p

) =0on∂D. (9.65)

This condition is identical to (9.56). It is deduced from the principle of macroscopic

thermodynamic equilibrium, rather than being an ad hoc proposition. It remains to

be seen whether it is sufﬁcient for the determination of φ and ψ if the domain is

known.

568 9 Magma Transport

9.4.5 Stefan Condition

The location of ∂D is not known apriori. Its determination is effected from a second

thermal boundary condition, which represents the energy balance across ∂D.This

is known as the Stefan condition, and takes the form

Lφ(v −V).n =



∂T

∂n



, (9.66)

where V is the velocity of ∂D. Scaling T −T

with T =ρ

gdΓ and V with [v]

leads to the dimensionless version of (9.66),

˜νφ(v

−V

) =−ε



∂

∂n

(z +˜νψ) −

∂T

∂n



on ∂D. (9.67)

In particular the part of the boundary where φ =0 is determined by the condition

∂T

∂n

∂

∂n

(z +˜νψ), (9.68)

and to leading order (neglecting ˜ν), this is independent of the partial melt dynamics.

9.4.6 Steady State Solution, One Dimension

Our conﬁdence in the prescription of the boundary conditions will be enhanced by

showing that solutions can be found which satisfy them. One way of doing this is

to ﬁnd explicit approximate solutions. To this end, we seek asymptotic solutions

for (9.50) and (9.55) based on the assumptions that ε, δ and ˜ν are small, but that

ν =O(1).

Speciﬁcally, we will consider steady state, one-dimensional solutions, which will

be appropriate if u =wk. In this case, the equations reduce to

2φφ

+ν





=φψ,

w[1 +˜νψ

−δφ

]=φψ +εψ

(9.69)

with anticipated boundary conditions

φ =0onz =0,ψ=0onz =1. (9.70)

In what follows we will suppose that w is constant.

9.4.7 Outer Solution

We put ε, ˜ν and δ to zero. Then φψ ≈w, and a ﬁrst integral of (9.69)

+νφ

=w(z +C), (9.71)

9.4 Melt Transport in the Asthenosphere 569

where C is constant. With ψ =w/φ, it follows that

νwφ

=φ

−w(z +C), (9.72)

which is a Riccati equation. It turns out that in order to obtain a coherent boundary

layer solution at z = 1, we need the solution of (9.72) which tends to inﬁnity at

z =1. The solution of (9.72) which does this is

φ =ν

1/3

2/3



Ai(ζ

)Bi



(ζ ) −Bi(ζ

)Ai



(ζ )

Bi(ζ

)Ai(ζ ) −Ai(ζ

)Bi(ζ )



, (9.73)

where

ζ =

z +C

(ν

1/3

,ζ

1 +C

(ν

1/3

. (9.74)

Direct consideration of (9.72) shows that there is a unique choice of φ

= φ|

z→0

such that φ →∞as z →1, providing C is not too small.

9.4.8 Boundary Layer at z =0

Near z =0, we put z =δZ, so that (9.69) becomes

2δφφ

+ν





=δ

φψ,



1 +

˜ν

−φ



=φψ +

(9.75)

Correct to O(δ),wehaveφ

= constant =0 to match to the outer solution ψ ∼

w/φ

as Z →∞, thus ψ =w/φ

+O(δ), and to leading order (9.75)

w(1 −φ

) =

wφ

, (9.76)

with solution

φ =φ



1 −e

−Z/φ



. (9.77)

This assumes that φ

> 0, which is certainly the case if C>0. This boundary layer

has been called the compaction layer.

9.4.9 Boundary Layer at z =1

As z →1, φ ∼νw/(1 −z), ψ ∼(1 −z)/ν, and thus we put

z =1 −δ

1/2

Z, φ =Φ/δ

1/2

,ψ=δ

1/2

Ψ ; (9.78)