Fowler A. Mathematical Geoscience

Подождите немного. Документ загружается.

570 9 Magma Transport

then (9.69) becomes

−2ΦΦ

+ν





=δ

3/2

ΦΨ,

w[1 −˜νΨ

+Φ

]=ΦΨ +

1/2

;

(9.79)

the matching conditions are

Φ ∼

νw

,Ψ∼

as Z →∞. (9.80)

To leading order, we have

−Φ

+νΦ

=0, (9.81)

and thus

Ψ =

, (9.82)

so that Ψ =0atZ =0. To leading order, Φ then satisﬁes

w(1 +Φ

) =

ZΦ

, (9.83)

and the (unique) solution which matches to the outer solution is

Φ =



∞

exp



−s

2νw



ds; (9.84)

in particular, Φ =(νwπ/2)

1/2

on Z =0, i.e.

φ ≈



νwπ

2δ



1/2

on z =1. (9.85)

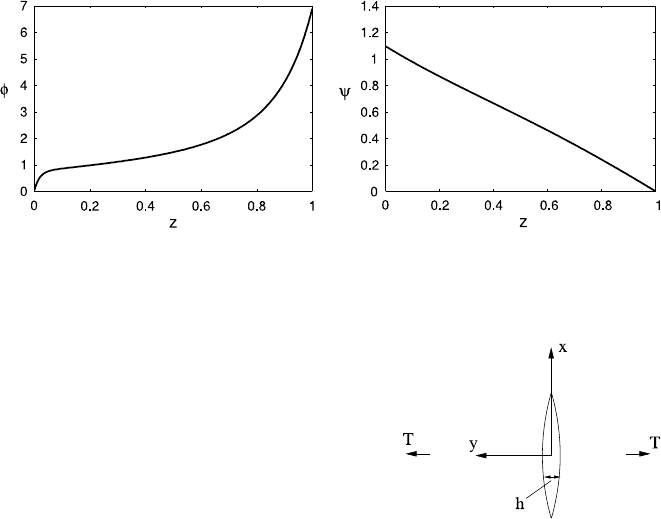
Figure 9.15 shows a numerical solution of the equations, which clearly shows the

boundary layer structure described above.

One of the more important consequences of this model and its solution is the

inference that the effective pressure ψ ∝p

−p

reaches zero at the upper bound-

ary where refreezing occurs. Since in practice the partial melting produces a buoy-

ant upwelling and thus a tensile stress in the mantle, this suggests that fracturing

is likely to occur at this interface, affording the possibility of magma migration

through the lithosphere. The fact that magma does indeed ascend through the litho-

sphere more or less implies that this does occur, but the formulation of the coupled

fractured/porous transport is not such an easy thing to carry out. Instead, we now

turn to the dynamic problem of describing how such fracture-driven transport can

occur.

9.5 Magmafracturing in the Lithosphere 571

Fig. 9.15 Numerical solution for φ and ψ of Eqs. (9.69) with the boundary conditions (9.70),

using values ν = 0.8, ˜ν = 0.12, w = 1, δ = 0.02, ε = 1.2 × 10

−3

. Very kindly provided by Ian

Hewitt

Fig. 9.16 A linear crack in

an elastic medium. A tension

T acts on the medium,

causing the crack to have a

width h

9.5 Magmafracturing in the Lithosphere

As magma oozes upwards in the asthenosphere, it ought to freeze as it reaches the

cold temperature of the lithosphere. The fact that magma reaches the surface of the

Earth implies that transport through the lithosphere is rapid, and the only apparent

way this can be accommodated is by the process of ‘magmafracturing’ (by analogy

to hydrofracturing). The buoyant magma ﬂows rapidly upwards in a conduit known

as a dyke, which is opened in the same way that a fracture propagates in a brittle

material. The speed of ascent, of the order of metres per second, is sufﬁciently rapid

that the lithosphere can be taken to respond elastically, and thus the width of the

crack is determined in terms of the ﬂuid pressure by quasi-static fracture mechanics

(because the ﬂuid speed is much less than the elastic wave speeds). To describe this

relationship, we now discuss linear elastic fracture mechanics.

9.5.1 Fracture Mechanics

We begin by dealing fairly generally with a crack as shown in Fig. 9.16.Wetake

axes x and y as shown, and consider the opening of a two-dimensional crack of

small width h when subjected to a tension T at inﬁnity superimposed on a lithostatic

pressure p

−ρ

gx. The ﬂuid pressure in the crack is taken to be p. In conditions

572 9 Magma Transport

of plane strain, the displacement vector has components (u, v), and the constitutive

law for linear elasticity

=2με

+λδ

, (9.86)

where λ and μ are the Lamé coefﬁcients, takes the simple form

=2μu

+λ(u

=2μv

+λ(u

τ =μ(u

);

(9.87)

x and y subscripts denote partial derivatives, and the three independent components

of the stress tensor are σ

≡σ

, σ

≡σ

, τ ≡σ

. The equations of motion are

∂σ

∂x

∂τ

∂y

−ρ

g =0,

∂τ

∂x

∂σ

∂y

=0.

(9.88)

We introduce complex variables

z =x +iy, ¯z =x −iy, (9.89)

and then the force balance equations can be written together as

∂

∂z

[σ

−σ

+2iτ]+

∂

∂ ¯z

(σ

+σ

) +

∂V

∂ ¯z

=0, (9.90)

where we deﬁne the real-valued potential

V =−ρ

g(z +¯z). (9.91)

The complex displacement is

D =u +iv, (9.92)

and then we ﬁnd

+σ

=2(λ +μ)(D

¯z

−σ

+2iτ =4μD

¯z

(9.93)

From this we ﬁnd that the force balance equations can be written in the form

∂

∂z

[4μD

¯z

∂

∂ ¯z



2(λ +μ)(D

¯z

)



∂V

∂ ¯z

=0, (9.94)

and thus there is a ﬁrst integral

4μD

+2(λ +μ)(D

¯z

) +V =

4(λ +2μ)

λ +μ



(z), (9.95)

9.5 Magmafracturing in the Lithosphere 573

where Ω(z) is an as yet arbitrary analytic function (the pre-multiplying coefﬁcient

is chosen for later algebraic simplicity).

We can solve this by ﬁrstly deriving an expression for D

and then integrating,

to ﬁnd

2μD =−

μX

2(λ +2μ)

+(¯z −z)



(z) +κΩ(z) +φ(¯z), (9.96)

where we deﬁne

∂X

∂z

=V, κ =

λ +3μ

λ +μ

, (9.97)

and φ is an arbitrary analytic function of ¯z (more precisely: φ(z) is an analytic

function of z, but its argument in (9.96)is¯z). See also Question 9.9.Fromthe

expressions in (9.93), we can now deduce the forms

+σ





(z) +Ω



(z)



−

(λ +μ)V

λ +2μ

−σ

+2iτ =−

μV

λ +2μ



(z) +2(¯z −z)Ω



(z) +2φ



(¯z),

−iτ =−

λV

2(λ +2μ)

+Ω



(z) −(¯z −z)Ω



(z) −φ



(¯z),

(9.98)

where we have used the fact that we can choose

∂X

∂ ¯z

=V (9.99)

(by choosing X to be real, explicitly X =−

g(z +¯z)

So far this is all quite general. Now we consider the situation shown in Fig. 9.16.

There is a crack which we denote by L on the x-axis, across which the functions Ω

and φ will typically be discontinuous; thus L will be a branch cut for these functions.

The boundary conditions for the stresses can be expressed in the form

+σ

→−2p

+ρ

g(z +¯z),

−σ

+2iτ →−2T as z →∞,

(9.100)

and

−iτ =−p,

2μ[D]

−

=2iμh for z ∈L,

(9.101)

where p denotes the ﬂuid pressure in the crack, and [D]

−

−D

−

denotes the

jump in D across L, from y =0− to y =0+.

Now note that, for any function g(z), g(¯z)

=g(z)

−

and g(¯z)

−

=g(z)

. Since

−iτ is continuous across L, we see from (9.98) that





(z) −φ



(¯z)



−

=0, (9.102)

574 9 Magma Transport

and thus that Ω



(z) +φ



(z) is an entire function. To ascertain what it is, we need the

limiting behaviours of Ω



and φ



at ∞. These we obtain from (9.98) and (9.100);

using the deﬁnition of V in (9.91), we ﬁnd



(z) ∼−

μρ

2(λ +2μ)



(¯z) ∼−T +

−

3μρ

g¯z

2(λ +2μ)

as z →∞,

(9.103)

from which it follows that



(z) +φ



(z) =−T −

μρ

λ +2μ

. (9.104)

Substituting for φ



(¯z) in (9.98)

, and letting z → x + i0 (thus Ω



(z) → Ω



(x),



(¯z) →Ω



−

(x)), we then ﬁnd



+Ω



−

=−T −



λ +μ

λ +2μ



gx −p on L. (9.105)

A second condition on L follows from (9.101)

. Using the fact that Ω + φ is

analytic, (9.96)impliesthat

[2μD]

−

=(1 +κ)(Ω

−Ω

−

), (9.106)

and thus (9.101)

yields

−Ω

−

2iμh

1 +κ

on L. (9.107)

Together with the boundary condition (9.103)

,(9.107) provides a Hilbert problem

for the determination of Ω in terms of h;(9.105) then determines the crack ﬂuid

pressure p in terms of h.

The solution of (9.107) with (9.103)

Ω(z) =

2πi



2iμh(s)ds

(1 +κ)(s −z)

−

z +

μρ

4(λ +2μ)

, (9.108)

from which the Plemelj formulae imply

+Ω

−

πi

−



2iμh(s)ds

(1 +κ)(s −x)

−p

x +

μρ

2(λ +2μ)

. (9.109)

Differentiating this and using (9.105), we ﬁnally obtain

p =P −

2π(1 −ν)

−



∂h

∂s

s −x

, (9.110)

9.5 Magmafracturing in the Lithosphere 575

where

P = p

−T −ρ

gx (9.111)

is the lithostatic compressive normal stress, and

ν =

2(λ +μ)

(9.112)

is Poisson’s ratio.

9.5.2 Magma Dynamics

So far we have not speciﬁed anything about the crack L. Now we consider a sit-

uation which is appropriate to the formation of a dyke growing upwards from the

asthenosphere. We imagine that the dyke originates at the asthenosphere, where we

take x = 0, and a ﬂux of magma Q(t) is injected into the crack. We suppose, not

very realistically, that the crack can be represented as having a symmetric extension

below the asthenosphere, so that the crack L is the interval (−l,l), where l(t) is the

lithospheric length of the crack, but we are concerned only with the region x>0.

The crack is thin, in the sense that its width h l, and thus the ﬂuid ﬂow in the

crack is given by the local Poiseuille ﬂow law

q =−

12η



∂p

∂x

+ρ



, (9.113)

where q is the ﬂuid ﬂux per unit transverse width of the crack, η

is the magma

viscosity, and ρ

is the magma density. Conservation of mass of ﬂuid in the crack

requires

∂h

∂t

∂q

∂x

=0. (9.114)

The three Eqs. (9.114), (9.113) and (9.110) provide the elastohydrodynamic model

for magmafracturing in the lithosphere.

9.5.3 Stress Intensity Factor

One boundary condition which we apply for (9.114) is the speciﬁed ﬂux at the inlet:

q =Q(t) at x =0. (9.115)

Another condition is necessary at the crack tip, and this is determined by a quantity

called the stress intensity factor.

576 9 Magma Transport

The stress intensity factor is associated with the stress ﬁeld generated by a crack

in a medium. In the simplest situation, a uniform crack overpressure σ generates a

singular stress ﬁeld in the solid, which has the asymptotic form

√

2πr

(θ), (9.116)

where the quantity K is known as the stress intensity factor, and the polar angle θ is

measured from an axis along, and in the opposite direction to, the crack. For mode

I cracks such as those considered here, we may deﬁne

K = lim

x→l+

√

2πxσ

y=0

. (9.117)

For a crack of length 2l, the stress intensity factor is

K =Yσ

√

πl, (9.118)

where Y is an O(1) numerical factor, associated with the crack geometry and the

conditions of loading.

Cracks can exist as perfectly good stationary features in an elastic medium, but

it is found that if the induced stress intensity factor K is large enough, then a crack

will grow. There is a critical stress intensity factor K

, such that when K reaches K

dynamic fracture occurs, and crack growth occurs at near elastic wave speeds—very

rapidly—and elastic waves are generated which propagate away from the source.

These are the seismic waves associated with crack propagation in earthquakes.

However, crack growth also occurs at values of K<K

, albeit less rapidly. This

is the phenomenon of subcritical crack propagation due to ‘stress corrosion’, and is

familiar to us all in the cracks that migrate slowly across a pane of glass. A grander

example is the rifting event which broke up Gondwanaland to form the Atlantic

ocean. The crack propagated from south to north over a period of tens of millions

of years.

It is found experimentally that the crack tip speed v is an increasing function of

K, becoming very large as K →K

. At low values of K, it becomes exponentially

small, and at higher values it reaches a plateau, before its asymptotic rise near K

The growth of cracks is essentially a thermodynamic process, being facilitated by

the release of energy to form new crack surface and thus surface energy. At K =K

this energy is directly released from the stored elastic energy in the medium. At

lower K, this is not enough, and the energy is thought to be supplied from chemical

or potential energy of the ﬂuid which migrates into the crack. It is then supposed

that the crack speed is determined by the rate-limiting energy supply mechanism.

At very low K, this is due to diffusion of chemical corrosive agents to the crack tip

(hence the term stress corrosion), and on the plateau at higher K, it is thought to be

controlled by the rate of ﬂuid migration to the crack tip.

It is this plateau region which is relevant here, and thus we may suppose that the

crack tip speed v will be controlled by the value of the stress intensity factor,

v =v(K), (9.119)

9.5 Magmafracturing in the Lithosphere 577

where v may be a weakly increasing function of K<K

. For what it is worth,

values of K

for crustal rocks have typical values K

∼ 10

Pa m

1/2

, though the

extrapolation of such values to the deep lithosphere may be hazardous.

9.5.4 Non-dimensionalisation and Solution

We use (9.112) to write (9.113) in the form

q =−

12η



−ρ

g −

∂Π

∂x



, (9.120)

where

ρ

=ρ

−ρ

, (9.121)

and

Π =

2π(1 −ν)

−



∂h

∂s

s −x

, (9.122)

and then we scale the variables by writing

q ∼Q

,h∼h

,Π∼Π

,x,l∼d

,t∼t

, (9.123)

where Q

is the order of the inlet ﬂux, d

is a typical lithosphere thickness, and

suitable balances of the equations suggest we choose



12η

ρ



1/3

,Π

μh

(1 −ν)d

. (9.124)

Then the dimensionless equations take the form

∂h

∂t

∂q

∂x

=0,

q =h



1 +δ

∂Π

∂x



Π =

2π

−



∂h

∂s

s −x

(9.125)

where

δ =

ρ

. (9.126)

If we take values ρ

=3 ×10

kg m

−3

, ρ

=2.5 ×10

kg m

−3

, g = 10 m s

−2

μ = 2 ×10

Pa, ν =0.25, Q

= 1m

−1

, η

= 10

Pa s, d

= 50 km, then we

ﬁnd h

=0.6m,t

=3 ×10

s, Π

=0.3 ×10

Pa, and thus δ ∼10

−3

. The natural

scale over which the singular integral term is important is of the order of 50 m, and

is inconsequential over the bulk of the ﬂow.

578 9 Magma Transport

If we take the limit δ → 0, the solution of the model is straightforward. Sup-

pose, for example, that the dimensionless ﬂux q = 1 at the asthenosphere x = 0.

Ignoring δ,wehaveq =h

, and h satisﬁes the hyperbolic equation

+3h

=0, (9.127)

and the solution for a crack starting at x =0att =0issimplyh =1for0<x<t;

the crack tip moves at unit speed to accommodate the inﬂux of magma at the as-

thenosphere. In dimensional terms, this is d

∼1.7ms

−1

This solution is invalid near the crack tip, where we must have h →0. There is

thus a boundary layer near the tip in which we put

x =t −



X, Π =

√

2δ

(9.128)

(the extra factor 2 is for cosmetic reasons), and then to leading order we ﬁnd q =h,

whence

=1 −

,Θ≈

−



∞

∂h

∂ξ

dξ

ξ −X

. (9.129)

The conditions on (9.129) are that h → 1asX →∞and h =0atX =0. More

speciﬁcally, we now use the prescription for the stress intensity factor. Since the

crack speed is determined by the magma ﬂow,

the condition (9.119) would appear

to determine K. Speciﬁcally, we use the deﬁnition of Ω in (9.108) to compute Ω



and thus σ

+σ

from (9.98). The local behaviour of the singular integral near the

crack tip then shows that if (dimensionally) h ∼c(l −x)

1/2

near the crack tip x =l,

then the stress is singular, as in (9.116), and the stress intensity factor is

K =

μc

√

2(1 −ν)

(9.130)

(see Question 9.9). Then we ﬁnd that the required behaviour of (dimensionless) h

satisfying (9.129) near X =0 is that

h ∼2λX

1/2

, (9.131)

where

λ =





K(1 −ν)

μh



. (9.132)

Numerical solution of (9.129) appears to show that there is a unique solution

for h, in which there is a slightly bulbous crack head, and the value of λ ≈ 1.3is

determined automatically. Our interpretation of this is that this prescription is actu-

ally telling us theoretically what the appropriate value of the subcritical crack speed

In Dave Stevenson’s phrase, the tail wags the dog.

9.6 Crystallisation in Magma Chambers 579

(9.119) is in this case. That is, we can determine the form of (9.119) by considera-

tion of the elastodynamical problem. Deﬁning the crack speed as v = Q

, and

using (9.124) and (9.132), we ﬁnd

v =

ρ

g(1 −ν)

6πλ

. (9.133)

Using the values we introduced earlier, we ﬁnd that this is

v =2.2 ×10

−6

[l][K]

−1

, (9.134)

where l =[l] km, K =[K] MPa m

1/2

. With [l]=50, we obtain crack speeds of

∼1ms

−1

if K ∼ 10

MPa m

1/2

. This is a good deal larger (twenty to a hundred

times) than measured critical stress intensity factors in the crust, and requires that K

increases substantially with pressure, in order that this magmafracturing be aseis-

mic. This seems not unreasonable.

The elastodynamic propagation of magma through the lithosphere is thus dynam-

ically feasible, although other questions remain, in particular the ﬂow needs to be

sufﬁciently rapid that the magma does not freeze as it ascends. This is fairly simple

to evaluate. If the Péclet number of the ﬂuid ﬂow is large, then there will be thermal

boundary layers at the walls which will provide a much larger heat ﬂux to the walls

than can be conducted away by the country rock; the magma will in fact melt back

the lithosphere (thus contaminating the chemistry of the host magma). For a magma

velocity ∼v ∼ 1ms

−1

, crack width h ∼1 m, crack length l ∼ 50 km, and thermal

diffusivity κ ∼ 10

−6

−1

, the reduced Péclet number Pe =

κl

∼ 20, suggest-

ing that even over such lengths, meltback of the channel walls is the more likely

occurrence.

The principal outstanding question is then the issue of providing a suitable inlet

boundary condition for the lithospheric fracture. Essentially, we need to glue to-

gether the porous magma transport in the asthenosphere with the fracture transport

in the lithosphere. It is not obvious how to do this. Apart from the tendency for

the magma compaction dynamics to allow fracture at the base of the lithosphere,

the magma transport solutions themselves are unstable in two dimensions to the

formation of magma channels. We might then expect a river-like system in the as-

thenosphere which simply continues to ﬂow upwards through the sub-freezing litho-

sphere, and providing the upwards ﬂow can be accommodated by accumulation in a

magma chamber, vented by eruptions, such a drainage system could be maintained

in a steady state. We now turn our attention to processes in magma chambers.

9.6 Crystallisation in Magma Chambers

It is generally accepted that magma initially propagates through the lithosphere by

the process of magmafracturing. The danger of freezing requires the ascent to be

rapid, and crack propagation is the only serious way for this to happen. One might

suppose that the magma would continue to ascend to the Earth’s surface, but this