Гайдук А.Р. Непрерывные и дискретные динамические системы
Подождите немного. Документ загружается.


71
(2.80) и находим (n–1)-у производную по времени от полученной функ-
ции y(t). Затем в найденных выражениях полагаем t=0 и приравниваем
каждое из них соответствующему начальному значению.
В результате снова получим систему линейных алгебраических урав-
нений, решение которой определяет все неизвестные постоянные
ii
c ψ ,
,
i
ϕ
в выражениях (2.83) и (2.80).
Пример 2.13. Найти решение уравнения
teyyy
t
cos3102
2−
=++
&&&
(2.91)
при
2 ,1
00
== yy
&
.
Решение. Характеристическое уравнение согласно (2.82) в данном
случае имеет вид
0102
2
=++ pp
. (2.92)
Его корни
jp 31
2,1
±−=
– комплексно-сопряженные числа, веществен-
ных нет. Следовательно, общее решение однородного дифференциально-
го уравнения (2.81), соответствующего уравнению (2.91), имеет вид
)3cos( )( ϕ+ψ=
−
tety
t
общ
(2.93)
или
]3sinsin3coscos[)( ttety
t
общ
ϕψ−ϕψ=
−
. (2.94)
Здесь
ψ
и
ϕ
– постоянные, подлежащие определению.
Правая часть уравнения (2.91) имеет вид (2.85) при
1 ,2
=
β
−
=
k
0)( ,3)(
21
== tGtG
, т.е.
0 ,0
21
== mm
. Комплексное число
=
β
+
jk
j12
+
−
не совпадает с корнями характеристического уравнения (2.92),
поэтому частное решение уравнения (2.91) имеет вид (2.87), (2.89) при
0}0,0max{
=
=
m
, т.е.
[
]
tqtqety
t
част
sincos)(
2010
2
+=
−
. (2.95)
Для определения
10
q
и
20
q
найдем производные
[
]
[
]
cossinsincos2)(
2010
2
2010
2
=+−++−=
−−
tqtqetqtqety
tt
част
&
72
]cos)2(sin)2([
10201020
2
tqqtqqe
t
−++−=
−
, (2.96)
+−++−−=
−
]cos)2(sin)2([2)(
10201020
2
tqqtqqety
t
част
&&
=−−+−+
−
]sin)2(cos)2([
10201020
2
tqqtqqe
t
]cos)43(sin)34[(
20102010
2
tqqtqqe
t
−++=
−
. (2.97)
Подставляя (2.95), (2.96) и (2.97) в (2.91), получим
+−++
−
]cos)43(sin)34[(
20102010
2
tqqtqqe
t
+−++−+
−
]cos)2(sin)2([2
10201020
2
tqqtqqe
t
[
]
tetqtqe
tt
cos3sincos10
2
2010
2 −−
=++
.
Сокращая на
t
e
2−
и приводя подобные в левой части этого равенства,
будем иметь
ttqqtqq cos3cos)29(sin)92(
20102010
=−++
или
.329 ;092
20102010
=−=+ qqqq
Решив эту систему, найдем
.0706,0 ;3177,0
2010
−== qq
Итак, согласно (2.95)
[
]
ttety
t
част
sin0706,0cos3177,0)(
2
−=
−
, а
по (2.80) и (2.94)
[
]
+ϕψ−ϕψ=
−
ttety
t
3sinsin3coscos)(
[
]
tte
t
sin0706,0cos3177,0
2
−+
−
. (2.98)
Для определения постоянных
ψ
и
ϕ
найдем производную по вре-
мени от функции
)(ty
из предыдущего равенства
)sin0706,0cos3177,0(2
)3sinsin3coscos()(
2
+−−
−ϕψ−ϕψ−=
−
−
tte
ttety
t
t
&
73
=−−+
+ϕψ−ϕψ−+
−
−
)cos0706,0sin3177,0(
)3cossin33sincos3(
2
tte
tte
t
t
. )0,1765sin0,706cos(
)3sin)cos3(sin3cos)3sincos((
2
tte
tte
t
t
−−+
+ϕ−ϕψ+ϕ+ϕψ−=
−
−
Полагая t=0 и принимая во внимание заданные начальные условия
2 ,1
00
== yy
&
, получим систему
( )
.2706,0sin3cos
,
1
3177
,
0
cos
=−ϕ+ϕψ−
=
+
ϕ
ψ
Решение этой системы дает
1294,1sin ,6816,0cos
−
=
ϕ
ψ
=
ϕ
ψ
. Отсюда
o
85,58 ;32,1 −=ϕ=ψ
. Подставляя эти значения в выражение (2.98) с
учетом равенства (2.93), найдем окончательно
)53,12cos(3255,0)85,583cos(32,1)(
2 oo
++−=
−−
tetety
tt
.
Операторный метод. Данный метод решения дифференциальных
уравнений основан на применении преобразования Лапласа искомого
решения y(t), уравнения (2.79) и функций, входящих в его правую часть
[6, 7]. Этот метод может применяться и в более общем случае, когда
дифференциальное уравнение имеет вид
=α+α++α+
−
−
)()(...)()(
01
)1(
1
)(
tytytyty
n
n
n
&
)(...)()(
)(
10
tgtgtg
m
m
β++β+β=
&
, (2.99)
где
)(tg
– дифференцируемая функция времени.
Операторный метод решения уравнений (2.79) или (2.99) более фор-
мализован и находит самое широкое применение при исследовании ди-
намических систем различного назначения, в особенности систем с одной
выходной переменной.
Для получения решения уравнения (2.79) или (2.99) при заданных
начальных условиях и функции
)(tg
(предполагается, что ее преобразо-
вание Лапласа g(p) – существует) в уравнении (2.79) или (2.99) функции
y(t) и g(t) заменяются их изображениями по Лапласу (см. § 1.2). В резуль-
тате, например, уравнение (2.99) принимает вид
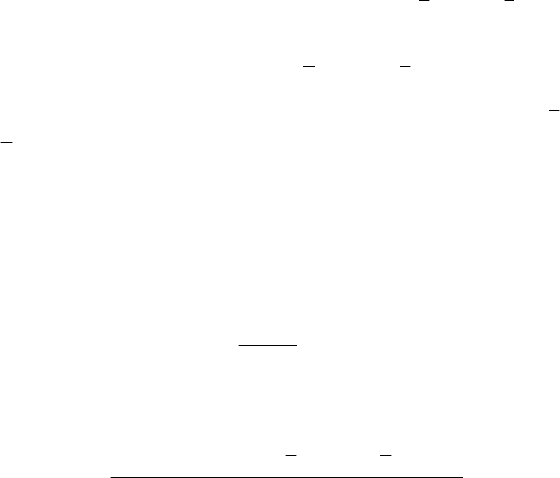
74
=α+α++α+
−
−
)()...(
01
1
1
pyppp
n
n
n
),(),()()...(
0010
ypAgpBpgpp
m
m
+−β++β+β=
или
),(),()()()()(
00
ypAgpBpgpBpypA +−=
, (2.100)
где y(p) и g(p) – изображения решения y(t) и функции g(t);
),(
0
ypA
,
),(
0
gpB
– некоторые полиномы, коэффициенты которых являются
функциями коэффициентов
ii
βα ,
и начальных значений функций y(t),
g(t) и их производных по времени, соответственно.
В теории динамических систем чаще всего рассматриваются функ-
ции g(t), изображение по Лапласу которых является отношением двух
полиномов
)(
0
pG
и
)(pG
, т.е.
)(
)(
)(
0
pG
pG
pg =
. (2.101)
Поэтому согласно (2.100) и (2.101) изображение по Лапласу y(p)
решения y(t) также является дробно-рациональной функцией вида
(
)
)()(
)(),(),()()(
)(
000
pGpA
pGgpBypApGpB
py
−+
=
. (2.102)
Таким образом, для определения искомого решения y(t) уравнения
(2.99) достаточно найти обратное преобразование Лапласа от обеих час-
тей выражения (2.102). Проще всего это сделать или путем разложения
правой части (2.102) на сумму простейших дробей, или с помощью тео-
ремы о вычетах [7, 14]. Эти методы достаточно подробно освещены в
литературе и поэтому здесь не рассматриваются.
Пример 2.14. Найти решение уравнения
)(3)(15)(15)(8)( tgtgtytyty
&&&&
+
=
+
+
, (2.103)
если
)2(2exp)( 2, ,1
00
ttgyy −===
&
.
Решение. Записывая изображения по Лапласу функций и их произ-
водных по времени, получим
)()}({ pytyL
=
,
1)()}({
−
=
ppytyL
&
,
2)()}({
2
−−= ppyptyL
&&
,
)()}({ pgtgL
=
,
2)()}({
−
=
ppgtgL
&
. Поэтому
уравнение (2.103) в изображениях по Лапласу принимает вид
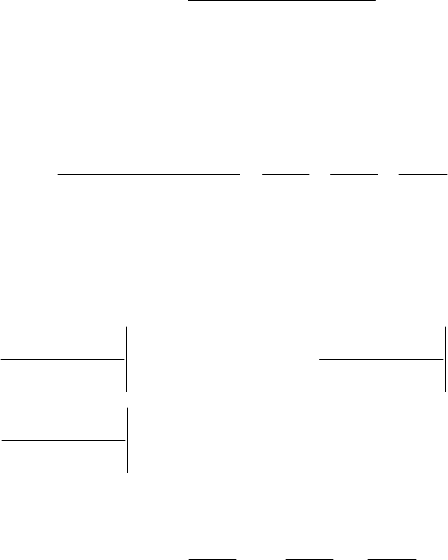
75
)10(6)()315()()158(
2
++−+=++ ppgppypp
. (2.104)
В рассматриваемом случае
)2/(2)}({
+
=
ptgL
(см. приложение
П.7), и поэтому из (2.104) следует равенство
)2)(158(
3812
)(
2
2
+++
++
=
ppp
pp
py
.
Так как корни уравнения
0158
2
=++ pp
равны –3 и –5, то изо-
бражение y(p) можно представить в виде суммы дробей следующим об-
разом
253)2)(5)(3(
3812
)(
2
+
+
+
+
+
=
+++
++
=
p
C
p
B
p
A
ppp
pp
py
, (2.105)
где А, В, С – неизвестные коэффициенты. Для их определения удобнее
всего умножить обе части правого равенства на один из знаменателей
простейших дробей и затем, после сокращения его, положить р равным
нулю этого знаменателя. В данном случае это дает
.6
)5)(3(
3812
,5.0
)2)(3(
3812
,5.5
)2)(5(
3812
2
2
5
2
3
2
=
++
++
=
=
++
++
=−=
++
++
=
−=
−=−=
p
pp
pp
pp
C
pp
pp
B
pp
pp
A
Итак, согласно (2.105), изображение искомого решения
2
1
6
5
1
5,0
3
1
5,5)(
+
+
+
+
+
−=
ppp
py
.
Совершая здесь обратное преобразование Лапласа (с помощью П.7),
найдем
ttt
eeepy
235
65,55,0)(
−−−
+−=
.
В заключение отметим, что процедура решения дифференциальных
уравнений операторным методом сохраняется той же самой и в том слу-
чае, когда комплексные числа
β
+
jk
в правой части дифференциального
уравнения (2.79), (2.85) совпадают с корнями характеристического урав-

76
нения (2.82). Изменяется в этом случае лишь способ нахождения обрат-
ного преобразования Лапласа.
Отметим также, что при решении уравнений (2.79) или (2.99) часто
применяется принцип суперпозиции, в особенности, когда сложная
функция g(t) может быть представлена суммой простых, элементарных
функций. Кроме того, в настоящее время для решения этих уравнений
широко применяются цифровые ЭВМ, программное обеспечение кото-
рых включает специальные программы [11].
§ 2.4. Решение систем дифференциальных уравнений
Однородная система. Допустим, задана следующая система диф-
ференциальных уравнений
Axx
=
&
, (2.106)
а также вектор начальных условий
0
x
. Задача заключается в отыскании
такой функции
)(tx
, чтобы уравнение
Axx
=
&
обращалось бы в тожде-
ство при всех
0
>
t
, а
0
)0(
xx
=
.
Рассмотрим вначале систему (2.106), но первого порядка
xx
α
=
&
.
Решение этого скалярного уравнения имеет вид
t
extx
α
=
0
)(
, (2.107)
где
0
x
– начальное значение,
t
e
α
– экспонента.
Как известно, экспонента может быть представлена рядом
K+
α
+
α
+=
α
!
2
!
1
1
22
tt
e
t
, (2.108)
который сходится при всех t. Известно также, что
tt
edtde
αα
α=
. В
этом можно убедиться, если продифференцировать по t ряд (2.108). По-
этому, подставляя (2.107) в уравнение
xx
α
=
&
, получим тождество
tt
exex
αα
α=α
00
.
Итак, в скалярном случае решение дифференциального уравнения
xx
α
=
&
при
0
)0( xx =
определяется выражением
0
)( xetx
tα
=
.
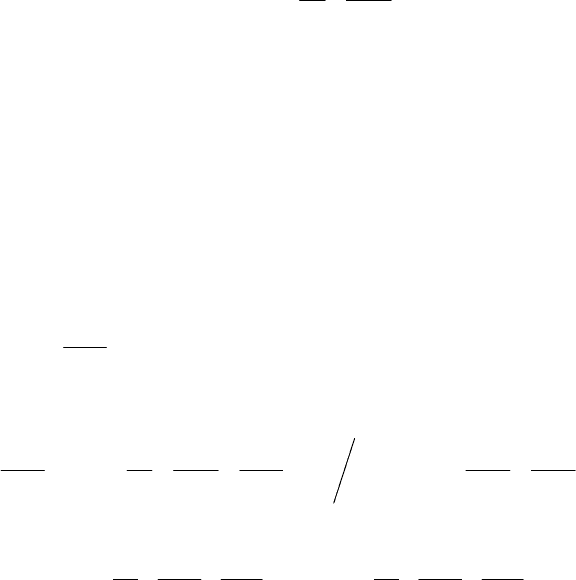
77
В векторном случае решение системы (2.106), по аналогии, ищется в
виде
0
)( xetx
At
=
, (2.109)
где
At
e
– матричная экспонента (см. П.5.3), которая также по аналогии с
обычной экспонентой (2.108) определяется рядом
K+++=
!
2
!
1
22
tAAt
Еe
At
(2.110)
В общем случае
ϕϕ
ϕϕ
=
)()(
)()(
1
111
tt
tt
e
nnn
n
At
K
MOM
K
,
т.е.
At
e
– это функциональная матрица.
Переходная матрица. Матрица
At
e
в теории динамических систем
называется п ере хо дной м атри цей.
Рассмотрим свойства переходной матрицы:
1.
Ee
A
=
⋅0
.
2.
AeAe
dt
de
AtAt
At
==
.
Доказательство. Дифференцируя ряд (2.110), получим
=
++++=
++++= KK
!2!1
0
!3!2!1
2323322
tAtA
Adt
tAtAAt
Ed
dt
de
At
A
tAtAAt
E
tAtAAt
EA
++++=
++++= KK
!3!2!1!3!2!1
33223322
.
Отсюда снова с учетом (2.110) следует справедливость свойства 2.
Таким образом, переходная матрица динамической системы, мате-
матическая модель которой имеет вид (2.106), также является решением
этого уравнения. При этом начальные условия равны единичной матрице,
78
т.е. если обозначить
)(te
tA
Φ=
, то можно записать
)()( tAt Φ=Φ
&
при
E
=
Φ
)0(
.
3.
0det ≠
tA
e
при всех t.
4.
AtAt
ee
−−
=
1
)(
Доказательство. По определению обратной матрицы
(
)
Eee
AtAt
=
−1
.
В данном случае имеем
Eeeee
ttAAAtAt
===
−− 0)(
,
что и требовалось доказать.
5. Если
321
ttt ≤≤
, то
2
232233
)()(
At
ttAtttAtA
eeee
−+−
==
– групповое
свойство матрицы
At
e
.
Аналогично,
1
13
112
233
)()()(
AtttAAtttAttAAt
eeeeee
−−−
==
.
6. Интеграл от переходной матрицы
∫
dte
At
.
Если
0det
=
A
, то интеграл вычисляется путем интегрирования ка-
ждого элемента матрицы
At
e
в отдельности.
Если же
0det
≠
A
, то существует
1−
A
. В этом случае
CAeCeAtde
tAtAtA
+=+=
−−
∫
11
,
где С – постоянная интегрирования (матрица).
Доказательство. Дифференцируя правую часть приведенного вы-
ражения для интеграла от
At
e
по t, получим
tAtA
eAeA =
−
1
.
Отсюда следует справедливость приведенного выражения для интеграла
от переходной матрицы
At
e
.
На основании указанных свойств переходной матрицы
At
e
легко убе-
диться, что формула (2.109) определяет решение уравнения (2.106).
Сопряженная система. Наряду с функцией
),(
0
xtx
, являющейся ре-
шением системы (2.106), определим функцию
),(
0
ψ
t
ψ
такую, что при всех

79
00
0
,, ψxtt ≥
выполняются условия
00
),0( ψψψ =
,
cψtψxtx
T
=),(),(
00
, где
с – произвольная постоянная. Оказывается, эта функция
(
)
),(
0
ψ
t
ψ
t
ψ =
является решением системы
ψ
A
ψ
T
−=
&
, (2.111)
которая называется сопряженной системе (2.106).
Решение сопряженной системы при начальном значении
0
ψ
определя-
ется, очевидно, выражением
0
)(
0
)( ψetψ
ttA
T
−−
=
, (2.112)
причем
cψx
T
=
0
0
.
Итак, для решения систем линейных дифференциальных уравнений ти-
па (2.106) необходимо уметь строить переходную матрицу
At
e
. Перейдем к
рассмотрению соответствующих методов.
Построение переходной матрицы. Канонические формы. Процесс
построения матрицы
At
e
зависит от вида матрицы А.
1. Пусть А – диагональная матрица. Для наглядности рассмотрим
сначала случай
2
=
n
, когда
λ
λ
=
1
1
0
0
A
.
Непосредственно по формуле (2.110) можно записать
=+
λ
λ
+
λ
λ
+=
K
2
2
2
1
2
2
1
0
0
!2
0
0
!1
10
01
tt
e
At
+
λ
+
λ
+
+
λ
+
λ
+
=
K
K
!2!1
10
0
!2!1
1
22
22
22
11
tt
tt
.
Итак, в частном случае диагональной матрицы второго порядка, т.е.
при
2
=
n

80
0
0
0
0
exp
2
1
2
1
=
λ
λ
=
λ
λ
t
t
tA
e
e
te
.
Аналогично, если А – диагональная матрица, то при любом n матри-
ца
At
e
тоже диагональная, причем ее элементами являются экспоненты,
показателями которых служат собственные числа матрицы А, т.е. если
][
21 n
diagA λλλ= K
, то
][)exp(
21
t
tt
At
n
eeediagAte
λ
λλ
== K
. (2.113)
2. Пусть матрица А имеет сопровождающую форму (2.15), т.е.
и различные собственные числа.
Как отмечалось выше, собственные числа матрицы
A
– это корни
i
λ
уравнения
0)det(
01
1
1
=α+λα+λα+λ=−λ
−
−
K
n
n
n
AE
. (2.114)
В данном случае по предположению
ji
λ≠λ
,
nji ,1, =
, (2.115)
поэтому определитель соответствующей матрицы Вандермонда
W
(2.17)
не равен нулю, т.е. существует обратная матрица
1−
W
.
Отличительным свойством матрицы Вандермонда является сле-
дующее. Если взять
W
в качестве преобразования подобия, то результи-
рующая матрица, как показано выше, будет диагональной, т.е.
][
~
21
1
n
diagAWWA λλλ==
−
K
– диагональная матрица.
Поэтому по формуле (2.113) можно записать
][
21
~
t
tt
tA
n
eeediage
λ
λλ
= K
.
,
1000
0100
0010
1210
−
−−−−
=
n
A
αααα
K
K
MOMMM
K
K
